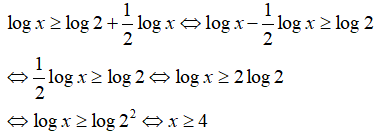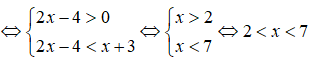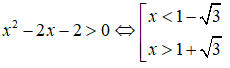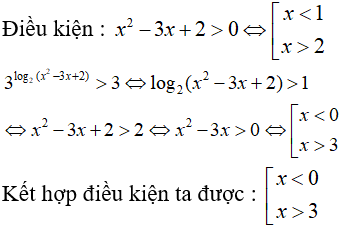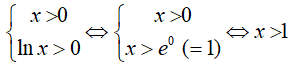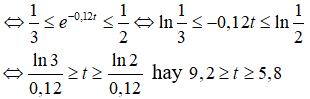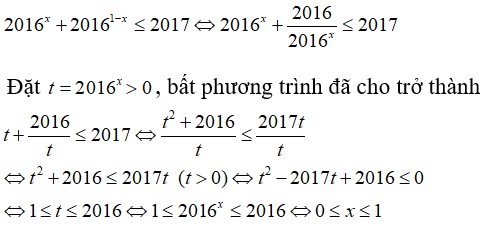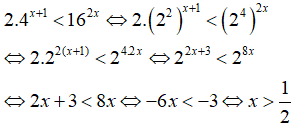TOP 40 câu Trắc nghiệm Bất phương trình mũ và bất phương trình Logarit (có đáp án 2024) - Toán 12
Bộ 40 câu hỏi trắc nghiệm Toán lớp 12 Bài 6: Bất phương trình mũ và bất phương trình Logarit có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 12 Bài 6.
Trắc nghiệm Toán 12 Bài 6: Bất phương trình mũ và bất phương trình Logarit
Bài giảng Trắc nghiệm Toán 12 Bài 6: Bất phương trình mũ và bất phương trình Logarit
Câu 1. Tìm tập nghiệm S của bất phương trình (2√5)1x≤(2√5)3.
A. S=(0;13).
B. S=(0;13].
C. S=(−∞;13].
D. S=(−∞;13]∪(0;+∞).
Đáp án: B
Giải thích:
Vì 2√5<1 nên bất phương trình
⇔1x≥3⇔1−3xx≥0
⇔0<x≤13.
Câu 2. Tìm tất cả các giá trị của x thỏa mãn (tanπ7)x2−x−9≤(tanπ7)x−1.
A. x≤−2.
B. x≥4.
C. −2≤x≤4.
D. x≤−2; x≥4.
Đáp án: D
Giải thích:
Do tanπ7<1 nên bất phương trình ⇔x2−x−9≥x−1
⇔x2−2x−8≥0
⇔[x≥4x≤−2.
Câu 3. Có bao nhiêu giá trị nguyên của trong đoạn [−2017;2017] thỏa mãn bất phương trình
A. 2013
B. 2017
C. 2014
D. 2021
Đáp án: C
Giải thích:
Bất phương trình 4x.33>3x.43
⇔4x3x>4333
⇔(43)x>(43)3
⇔x>3.
Vì x nguyên và thuộc đoạn [−2017;2017]
→x={4;5;6;...2017}.
Vậy có tất cả 2014 giá trị thỏa mãn.
Câu 4. Có tất cả bao nhiêu giá trị nguyên dương của x thỏa mãn bất phương trình 8x.21−x2>(√2)2x?
A. 2.
B. 3.
C. 4.
D. 5.
Đáp án: A
Giải thích:
Bất phương trình 8x.21−x2>(√2)2x
⇔23x.21−x2>2x
⇔23x+1−x2>2x
⇔3x+1−x2>x
⇔x2−2x−1<0
⇔1−√2<x<1+√2
Vậy tập nghiệm của bất phương trình là S=(1−√2;1+√2).
Suy ra các giá trị nguyên dương thuộc S là {1;2}.
Câu 5. Gọi là tập nghiệm của bất phương trình 31−x+2.(√3)2x≤7. Khi đó S có dạng [a;b] với a<b. Tính P=b+a.log23.
A. P=2.
B. P=1.
C. P=0.
D. P=2log23.
Đáp án: C
Giải thích:
Bất phương trình ⇔33x+2.3x≤7
⇔2.32x−7.3x+3≤0.
Đặt t=3x, t>0.
Bất phương trình trở thành 2t2−7t+3≤0
⇔12≤t≤3.
→12≤3x≤3
⇔−log32≤x≤1
→{a=−log32b=1
→P=b+a.log23=0.
Câu 6. Gọi a, b lần lượt là nghiệm nhỏ nhất và nghiệm lớn nhất của bất phương trình 3.9x−10.3x+3≤0. Tính P=b−a.
A. P=1.
B. P=32.
C. P=2.
D. P=52.
Đáp án: C
Giải thích:
Bất phương trình tương đương với 3.32x−10.3x+3≤0.
Đặt t=3x, t>0. Bất phương trình trở thành 3t2−10t+3≤0
⇔13≤t≤3.
→13≤3x≤3
⇔−1≤x≤1
→{a=−1b=1
→P=b−a=2.
Câu 7. Tìm tập nghiệm S của bất phương trình (x2+x+1)x<1.
A. S=(0;+∞).
B. S=(−∞;0).
C. S=(−∞;−1).
D. S=(0;1).
Đáp án: C
Giải thích:
Ta có x2+x+1=(x+12)2+34>0.
Bất phương trình tương đương với (x2+x+1)x<(x2+x+1)0.(*)
Nếu x2+x+1<1
⇔x2+x<0
⇔−1<x<0 thì (*)⇔x>0: không thỏa mãn.
Nếu x2+x+1>1
⇔x2+x>0
⇔[x<−1x>0 thì (*)⇔x<0.
Kết hợp điều kiện [x<−1x>0 ta được x<−1.
Vậy bất phương trình có tập nghiệm S=(−∞;−1).
Câu 8. Cho bất phương trình xlog2x+4≤32. Mệnh đề nào sau đây đúng?
A. Tập nghiệm của bất phương trình là một khoảng.
B. Tập nghiệm của bất phương trình là một đoạn.
C. Tập nghiệm của bất phương trình là nửa khoảng.
D. Tập nghiệm của bất phương trình là hợp của hai đoạn mà hai đoạn này giao nhau bằng rỗng.
Đáp án: B
Giải thích:
Điều kiện: x>0. Đặt log2x=t→x=2t.
Bất phương trình
⇔(2t)t+4≤32
⇔2t(t+4)≤25
⇔t2+4t≤5
⇔−5≤t≤1
→−5≤log2x≤1
⇔132≤x≤2
→S=[132;2].
Câu 9. Gọi a, b là hai nghiệm của bất phương trình xlnx+eln2x≤2e4 sao cho |a−b| đạt giá trị lớn nhất. Tính P=ab.
A. P=e.
B. P=1.
C. P=e3.
D. P=e4.
Đáp án: B
Giải thích:
Điều kiện: x>0. Ta có đẳng thức eln2x=(elnx)lnx=xlnx.
Do đó bất phương trình ⇔2.eln2x≤2.e4
⇔ln2x≤4
⇔|lnx|≤2
⇔−2≤lnx≤2
⇔e−2≤x≤e2
⇔1e2≤x≤e2
→{a=1e2b=e2
→P=ab=1.
Câu 10. (ĐỀ MINH HỌA 2016 – 2017) Cho hàm số f(x)=2x.7x2. Khẳng định nào sau đây là sai ?
A. f(x)<1⇔x+x2log27<0.
B. f(x)<1⇔xln2+x2ln7<0.
C. f(x)<1⇔xlog72+x2<0.
D. f(x)<1⇔1+xlog27<0.
Đáp án: D
Giải thích:
Ta có f(x)<1⇔2x.7x2<1.(*)
Lấy logarit cơ số 2 hai vế của (*), ta được log2(2x.7x2)<log21
⇔log22x+log27x2<0
⇔x+x2log27<0.
Do đó A đúng.
Lấy ln hai vế của (*), ta được ln(2x.7x2)<ln1
⇔ln2x+ln7x2<0
⇔xln2+x2ln7<0.
Do đó B đúng.
Lấy logarit cơ số 7 hai vế của (*), ta được log7(2x.7x2)<log71
⇔log72x+log77x2<0
⇔xlog72+x2<0.
Do đó C đúng.
Vì x∈ℝ nên từ kết quả của đáp án A, khẳng định x+x2log27<0
⇔x(1+xlog27)<0
⇔1+xlog27<0 là sai.
Câu 11. (ĐỀ MINH HỌA 2016 – 2017) Giải bất phương trình log2(3x−1)>3.
A. x>3.
B. 13<x<3.
C. x<3.
D. x>103.
Đáp án: A
Giải thích:
Bất phương trình ⇔3x−1>23
⇔3x>9⇔x>3.
Câu 12. Cho bất phương trình log13(x2−2x+6)≤−2. Mệnh đề nào sau đây là đúng?
A. Tập nghiệm của bất phương trình là nửa khoảng.
B. Tập nghiệm của bất phương trình là một đoạn.
C. Tập nghiệm của bất phương trình là hợp của hai nửa khoảng.
D. Tập nghiệm của bất phương trình là hợp của hai đoạn.
Đáp án: C
Giải thích:
Bất phương trình ⇔−log3(x2−2x+6)≤−2
⇔log3(x2−2x+6)≥2
⇔x2−2x+6≥9
⇔x2−2x−3≥0
⇔[x≥3x≤−1.
Vậy bất phương trình có tập nghiệm là S=(−∞;−1]∪[3;+∞).
Câu 13. Tìm tập nghiệm S của bất phương trình log15(x2−1)<log15(3x−3).
A. S=(2;+∞).
B. S=(−∞;1)∪(2;+∞).
C. S=(−∞;−1)∪(2;+∞).
D. S=(1;2).
Đáp án: A
Giải thích:
Điều kiện: {x2−1>03x−3>0⇔x>1.
Bất phương trình: log15(x2−1)<log15(3x−3)
⇔x2−1>3x−3(chú ý với cơ số 15<1)
⇔x2−3x+2>0
⇔[x>2x<1dk:x>1→x>2.
Câu 14. Tìm tập nghiệm S của bất phương trình loga(x2−x−2)>loga(−x2+2x+3), biết 94 thuộc S
A. S=(2;52).
B. S=(−1;52).
C. S=(−∞;−1).
D. S=(52;+∞).
Đáp án: A
Giải thích:
Điều kiện: {x2−x−2>0−x2+2x+3>00<a≠1
⇔{2<x<30<a≠1.
Do x=94 là nghiệm của bất phương trình đã cho nên loga1316>loga3916
→0<a<1.
Vì 0<a<1 nên bất phương trình ⇔x2−x−2<−x2+2x+3
⇔2x2−3x−5<0
⇔−1<x<52
dk: 2<x<3→2<x<52.
Câu 15. Tìm tập nghiệm S của bất phương trình lnx2>ln(4x−4).
A. S=(2;+∞).
B. S=(1;+∞).
C. S=ℝ\{2}.
D. S=(1;+∞)\{2}.
Đáp án: D
Giải thích:
Điều kiện: {4x−4>0x≠0⇔x>1.
Bất phương trình ⇔x2>4x−4
⇔x2−4x+4>0
⇔(x−2)2>0
⇔x≠2
Đối chiếu điều kiện, ta được tập nghiệm của bpt là S=(1;+∞)\{2}.
Câu 16. Gọi S là tập nghiệm của bất phương trình log0,3(4x2)≥log0,3(12x−5). Kí hiệu m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của tập S. Mệnh đề nào sau đây là đúng?
A. m+M=3.
B. m+M=2.
C. M−m=3.
D. M−m=1.
Đáp án: A
Giải thích:
Điều kiện: x≥512.
Bất phương trình ⇔4x2≤12x−5
⇔4x2−12x+5≤0
⇔12≤x≤52(thỏa mãn).
Suy ra tập nghiệm của bất phương trình là S=[12;52].
Suy ra m=12 và M=52 nên m+M=3.
Câu 17. Tìm tập nghiệm S của bất phương trình log10log(x2+21)<1+logx.
A. S=(3;7).
B. S=(−∞;3)∪(7;+∞).
C. S=(−∞;3).
D. S=(7;+∞).
Đáp án: A
Giải thích:
Điều kiện: x > 0
Bất phương trình
⇔log(x2+21).log10<log10+logx
⇔log(x2+21)<log(10x)
⇔x2+21<10x
⇔3<x<7(thỏa mãn)
→S=(3;7).
Câu 18. Có bao nhiêu số nguyên dương x thỏa mãn bất phương trình log(x−40)+log(60−x)<2?
A. 20.
B. 18.
C. 21.
D. 19.
Đáp án: B
Giải thích:
Điều kiện: 40<x<60.
Bất phương trình ⇔log[(x−40)(60−x)]<2
⇔(x−40)(60−x)<102
⇔x2−100x+2500>0
⇔(x−50)2>0⇔x≠50.
Kết hợp với điều kiện, ta được {40<x<60x≠50
x∈ℤ+→x∈{41;...;59}\{50}.
Câu 19. Biết rằng tập nghiệm của bất phương trình log2(1+log19x−log9x)<1 có dạng S=(1a;b) với a, b là những số nguyên. Mệnh đề nào sau đây là đúng?
A. a = -b.
B. a + b = 1.
C. a = b.
D. a = 2b.
Đáp án: C
Giải thích:
Điều kiện: {x>01+log19x−log9x>0
⇔{x>01−2log9x>0
⇔[x>0log9x<12
⇔{x>0x<3
⇔0<x<3.
Bất phương trình ⇔1−2log9x<2
⇔log9x>−12
⇔x>13.
Đối chiếu với điều kiện, ta được tập nghiệm của bất phương trình là S=(13;3).
Suy ra a=3, b=3.
Câu 20. Có bao nhiêu giá trị nguyên của x trong đoạn [−2018;2018] thỏa mãn bất phương trình log[log2(x+√2x2−x)]π4<0?
A. 4033
B. 4031
C. 4037
D. 2018
Đáp án: B
Giải thích:
Điều kiện: {x+√2x2−x>0(1)log2(x+√2x2−x)>0(2)
Bất phương trình log[log2(x+√2x2−x)]π4<log1π4
⇔log2(x+√2x2−x)>1 (thỏa )
⇔log2(x+√2x2−x)>log22
⇔x+√2x2−x>2 (thỏa )
⇔√2x2−x>2−x
⇔[{2−x<02x2−x≥0{2−x≥02x2−x>(2−x)2
⇔[x>1x<−4
![]()
có 4031 giá trị nguyên của x thỏa mãn.
Câu 21. Tìm tập nghiệm S của bất phương trình log2x+log3x>1+log2xlog3x.
A. S=(3;+∞).
B. S=(0;2)∪(3;+∞).
C. S=(2;3).
D. S=(−∞;2)∪(3;+∞).
Đáp án: C
Giải thích:
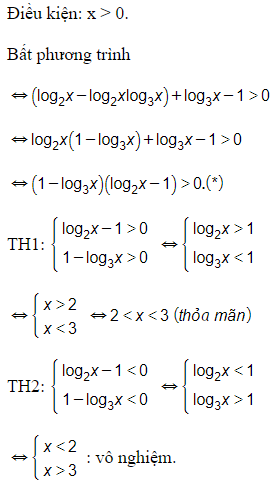
Vậy tập nghiệm của bất phương trình là S=(2;3).
Câu 22. Có tất cả bao nhiêu số nguyên thỏa mãn bất phương trình log[log2(2−x2)]12>0?
A. 1.
B. 2.
C. 3.
D. 0.
Đáp án: D
Giải thích:
Điều kiện: {2−x2>0log2(2−x2)>0
⇔{2−x2>02−x2>1
⇔2−x2>1
⇔−1<x<1.
Bất phương trình ⇔log[log2(2−x2)]12>log112
⇔log2(2−x2)<1
⇔log2(2−x2)<log22
Đối chiếu điều kiện, bất phương trình có tập nghiệm S=(−1;0)∪(0;1).
Suy ra không có số nguyên nào thuộc tập S.
Câu 23. Tìm tập nghiệm S của bất phương trình log12(log32x+1x−1)>0.
A. S=(−∞;1)∪(4;+∞).
B. S=(−∞;−2)∪(1;+∞).
C. S=(−2;1)∪(1;4).
D. S=(−∞;−2)∪(4;+∞).
Đáp án: D
Giải thích:
Điều kiện: {2x+1x−1>0log32x+1x−1>0
⇔{2x+1x−1>02x+1x−1>1
⇔2x+1x−1>1
⇔[x>1x<−2
Bất phương trình ⇔log32x+1x−1<1
⇔2x+1x−1<3
⇔4−xx−1<0
⇔[x<1x>4.
Đối chiếu điều kiện, ta được tập nghiệm S=(−∝;−2)∪(4;+∝).
Câu 24. Tìm tập nghiệm S của bất phương trình 1−log4x1−log2x≤12.
A. S=(0;2).
B. S=[2;+∞).
C. S=(−∞;2).
D. S=(2;+∞).
Đáp án: D
Giải thích:
Điều kiện: {x>0log2x≠1⇔{x>0x≠2.
Bất phương trình ⇔1−12log2x1−log2x≤12
⇔2−log2x2(1−log2x)≤12
⇔2−log2x1−log2x≤1
⇔2−log2x1−log2x−1≤0
⇔11−log2x≤0
⇔1−log2x<0
⇔log2x>1
⇔x>2(thỏa mãn).
Vậy tập nghiệm của bất phương trình là S=(2;+∞).
Câu 25. Tìm tất cả các giá trị thực của tham số m để bất phương trình (2e)x2+2mx+1≤(e2)2x−3m nghiệm đúng với mọi x.
A. m∈(−5;0).
B. m∈[−5;0].
C. m∈(−∞;−5)∪(0;+∞).
D. m∈(−∞;−5]∪[0;+∞).
Đáp án: B
Giải thích:
Bất phương trình ⇔(e2)−x2−2mx−1≤(e2)2x−3m
⇔−x2−2mx−1≤2x−3m
Ycbt ⇔x2+2(m+1)x−3m+1≥0,∀x∈ℝ
⇔{a>0Δ'≤0
⇔{1>0(m+1)2+3m−1≤0
⇔m2+5m≤0
⇔−5≤m≤0.
Câu 26. (ĐỀ CHÍNH THỨC 2016 – 2017) Tìm tất cả các giá trị thực của tham số để bất phương trình log22x−2log2x+3m−2<0 có nghiệm thực.
A. m<1.
B. m≤1.
C. m<0.
D. m<23.
Đáp án: A
Giải thích:
Điều kiện: x > 0.
Đặt t=log2x, với x > 0 suy ra t∈(− ∞;+ ∞).
Bất phương trình đã cho trở thành t2−2t+3m−2<0
⇔3m<− t2+2t+2 (∗).
Ycbt ⇔ phương trình (*) có nghiệm ⇔ 3m<max(− ∞; + ∞)g(t) với g(t)=− t2+2t+2.
Ta có g(t)=− t2+2t+2
=3−(t−1)2≤3, ∀t∈ℝ.
Suy ra max(− ∞; + ∞)g(t)=3.
Từ đó suy ra 3m<3⇔m<1 thỏa mãn yêu cầu bài toán.
Câu 27. Có bao nhiêu giá trị nguyên của tham số m để bất phương trình log5+log(x2+1)≥log(mx2+4x+m) đúng với mọi x?
A. 0.
B. 1.
C. 2.
D. 4.
Đáp án: B
Giải thích:
Để bất phương trình đúng với mọi khi và chỉ khi:
● Bất phương trình xác định với mọi x ⇔mx2+4x+m>0, ∀x∈ℝ
⇔{m>0Δ'<0
⇔{m>04−m2<0
⇔m>2. (1)
● Bất phương trình nghiệm đúng với mọi x
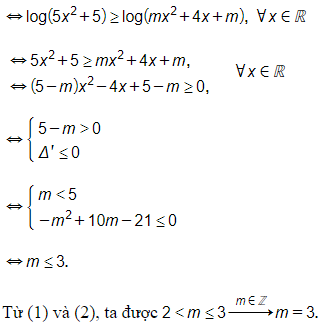
Câu 28. Có bao nhiêu giá trị m nguyên thuộc đoạn [−2017;2017] để bất phương trình logm(x2+2x+m+1)>0 đúng với mọi x?
A. 2015
B. 4030
C. 2016
D. 4032
Đáp án: C
Giải thích:
Để bất phương trình đúng với mọi khi và chỉ khi:
● Bất phương trình xác định với mọi x ⇔{x2+2x+m+1>0, ∀x∈ℝ0<m≠1
⇔{(x+1)2+m>0, ∀x∈ℝ0<m≠1⇔0<m≠1.
● Bất phương trình nghiệm đúng với mọi x ⇔logm(x2+2x+m+1)>0, ∀x∈ℝ.
Nếu m > 1 thì (*)⇔x2+2x+m>0, ∀x∈ℝ
⇔Δ'=1−m<0
⇔m>1: (thỏa mãn).
Nếu 0<m<1 thì (*)⇔x2+2x+m<0, ∀x∈ℝ
⇔{1<0Δ=1−m<0: vô lí.
Vậy m > 1 thỏa mãn yêu cầu bài toán
m∈[−2017;2017]→m∈ℤm∈{2;3;4;...;2017}.
Câu 29. Trong các số dương x thỏa mãn logx ≥ log2 + (1/2)logx
A. Số có giá trị lớn nhất là 1
B. Số có giá trị nhỏ nhất là 1
C. số có giá trị lớn nhất là 4
D. số có giá trị nhỏ nhất là 4
Đáp án: D
Giải thích:
Ta có
Số x nhỏ nhất là 4
Câu 30. Giải bất phương trình log5(2x - 4) < log5(x + 3)
A. 2 < x < 7
B. -3 < x < 7
C. -3 < x < 2
D. x < 7
Đáp án: A
Giải thích:
log5(2x - 4) < log5(x + 3)
Câu 31. Giải bất phương trình ln(xx - 2x - 2) < 0
A. -1 ≥ x ≥ 3.
B. -1 - √3 < x < 1 + √3.
C. x ∞[-1; 1 - √3) ∪ (1 + √3).
D. x ∞ (1 + √3), 3].
Đáp án: D
Giải thích:
Điều kiện
Khi đó BPT ⇔ x2 - 2x - 2 ≤ e0 = 1 ⇔ x2 - 2x - 3 ≤ 0 ⇔ -1 ≤ x ≤ 3
Kết hợp được tập nghiệm: (1 + √3; 3)
Câu 32. Giải bất phương trình logx + log(x + 9) > 11
A. 0 < x < 3.
B. x < 0 hoặc x > 3.
C. x < 1 hoặc x > 2.
D. x > 1.
Đáp án: D
Giải thích:
Điều kiện x > 0. Khi đó bất phương trình đã cho tương đương với
log[x(x + 9)] > 1 ⇔ x(x + 9) > 10 ⇔ x2 + 9x - 10 > 0
⇔ x < -10 hoặc x > 1 ⇔ x > 1 (do x > 0)
Câu 33. Giải bất phương trình 3log2(x2 - 3x + 2) > 3
A. 0 < x < 3
B. x < 0 hoặc x > 3
C. x < 1 hoặc x > 2
D. 0 < x < 1 hoặc 2 < x < 3
Đáp án: B
Giải thích:
Câu 34. Tìm miền xác định của hàm số y = ln(lnx)
A. D = (e; +∞)
B. D = [e; ∞)
C. D = (0; +∞)
D. D = (1; +∞)
Đáp án: D
Giải thích:
Điều kiện
Câu 35. Giá trị của một chiếc xe ô tô sau t năm được ước lượng bằng công thức G(t) = 600e-0,12t (triệu đồng). Để bán lại xe với giá trừ 200 triệu đến 300 triệu đồng, người chủ phải bán trong khoảng thời gian nào kể từ khi mua (làm tròn kết quả đến hàng phần mười của năm)?
A. Từ 2,5 đến 4,0 năm
B. Từ 4,0 đến 9,2 năm
C. Từ 4,0 đến 6,2 năm
D. Từ 5,8 đến 9,2 năm
Đáp án: D
Giải thích:
Yêu cầu đề bài : 200 ≤ 600e-0,12t ≤ 300
Câu 36. Giải bất phương trình 2016x + 20161 - x ≤ 2017
A. 1 ≤ x ≤ 2016
B. 0 ≤ x ≤ 1
C. x ≤ 1 hoặc x ≥ 2016
D. x ≤ 0 hoặc x ≥ 1
Đáp án: B
Giải thích:
Ta có:
Chọn đáp án B
Câu 37. Tìm tập nghiệm của bất phương trình log(x - 21) < 2 - logx
A. (-4; 25)
B. (0; 25)
C. (21; 25)
D. (25; +∞)
Đáp án: C
Giải thích:
Điều kiện x > 21. Khi đó:
log(x - 21) < 2 - logx ⇔ log(x - 21) + logx < 2
⇒ log[x(x - 21)] < 2 ⇒ x(x - 21) < 102
⇔ x2 - 21x - 100 < 0
⇔ -4 < x < 25
Kết hợp điều kiện x > 21, ta được 21 < x < 25.
Câu 38. Giải bất phương trình 2.4x + 1 < 162x
A. x > 1
B. x < 1
C. x > 1/2
D. x < 1/2
Đáp án: C
Giải thích:
Câu 39. Giải bất phương trình 2x.3x ≤ 36
A. x ≤ 2
B. x ≤ 3
C. x ≤ 6
D. x ≤ 4
Đáp án: A
Giải thích:
2x.3x ≤ 36 ⇔ 6x ≤ 62 ⇔ x ≤ 2
Câu 40. Giải bất phương trình 7.3x + 1 + 5x + 3 ≤ 3x + 4 + 5x + 2
A. x ≤ -1
B. x ≥ -1
C. x ≤ 0
D. x ≥ 0
Đáp án: A
Giải thích:
Các câu hỏi trắc nghiệm Toán lớp 12 có đáp án, chọn lọc khác:
Trắc nghiệm Ôn tập Chương 2 có đáp án
Trắc nghiệm Nguyên hàm có đáp án
Trắc nghiệm Tích phân có đáp án
Trắc nghiệm Ứng dụng tích phân có đáp án
Trắc nghiệm Ôn tập Chương 3 - Nguyên hàm - Tích phân và ứng dụng có đáp án
Xem thêm các chương trình khác:
- Trắc nghiệm Sinh học lớp 7 có đáp án
- Trắc nghiệm Toán lớp 7 có đáp án
- Trắc nghiệm Ngữ văn lớp 7 có đáp án
- Trắc nghiệm Sinh học 8 có đáp án
- Trắc nghiệm Toán lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn 8 có đáp án
- Trắc nghiệm Hóa học lớp 8 có đáp án
- Trắc nghiệm Địa Lí lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Tiếng Anh lớp 8 có đáp án
- Trắc nghiệm GDCD lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Lịch sử lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Vật Lí lớp 8 có đáp án
- Trắc nghiệm Công nghệ lớp 8 có đáp án
- Trắc nghiệm Tin học lớp 8 có đáp án
- Trắc nghiệm Sinh học lớp 9 có đáp án
- Trắc nghiệm Toán lớp 9 có đáp án
- Trắc nghiệm Ngữ văn 9 có đáp án
- Trắc nghiệm Hóa học lớp 9 có đáp án
- Trắc nghiệm Địa lí lớp 9 có đáp án
- Trắc nghiệm Tiếng Anh lớp 9 có đáp án
- Trắc nghiệm GDCD lớp 9 có đáp án
- Trắc nghiệm Lịch sử lớp 9 có đáp án
- Trắc nghiệm Vật lí lớp 9 có đáp án
- Trắc nghiệm Công nghệ lớp 9 có đáp án
- Trắc nghiệm Sinh học lớp 10 có đáp án
- Trắc nghiệm Toán lớp 10 có đáp án
- Trắc nghiệm Hóa học lớp 10 có đáp án
- Trắc nghiệm Ngữ văn lớp 10 có đáp án
- Trắc nghiệm Vật Lí lớp 10 có đáp án
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án
- Trắc nghiệm Sinh học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Toán lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Hóa học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn lớp 11 có đáp án
- Trắc nghiệm Tiếng Anh lớp 11 có đáp án
- Trắc nghiệm Vật Lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Địa lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm GDCD lớp 11 có đáp án
- Trắc nghiệm Lịch sử lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Công nghệ lớp 11 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 11 có đáp án
- Trắc nghiệm Tin học lớp 11 có đáp án