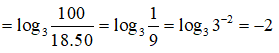TOP 40 câu Trắc nghiệm Logarit (có đáp án 2024) - Toán 12

Trắc nghiệm Toán 12 Bài 3: Logarit

Bài giảng Toán 12 Bài 3: Logarit

Câu 1. Cho các mệnh đề sau:

(I). Cơ số của logarit phải là số nguyên dương.

(II). Chỉ số thực dương mới có logarit.

(III). $\ln \left(A+B\right)=\ln A+\ln B$ với mọi $A>0,B>0$.

(IV) ${\log }_{a}b.{\log }_{b}c.{\log }_{c}a=1$, với mọi $a,b,c\in ℝ$.

Số mệnh đề đúng là:

A. 1.

B. 2.

C. 3.

D. 4.

Hiển thị đáp án

Đáp án: A

Giải thích:

Cơ số của lôgarit phải là số dương khác 1. Do đó (I) sai.

Rõ ràng (II) đúng theo lý thuyết SGK.

Ta có $\ln A+\ln B=\ln \left(A.B\right)$ với mọi $A>0,B>0$. Do đó (III) sai.

Ta có ${\log }_{a}b.{\log }_{b}c.{\log }_{c}a=1$ với mọi $0<a,b,c\ne 1$. Do đó (IV) sai.

Vậy chỉ có mệnh đề (II) đúng.

Câu 2. Cho $a,A,B,M,N$ là các số thực với $a,M,N$ dương và khác 1. Có bao nhiêu phát biểu đúng trong các phát biểu dưới đây?

(I). Nếu $C=\sqrt{AB}$ với $AB>0$ thì $2\ln C=\ln A+\ln B$

(II). $\left(a-1\right){\log }_{a}x\ge 0\iff x\ge 1$

(III). $M^{{\log }_{a}N}=N^{{\log }_{a}M}$

(IV). $\underset{x\to +\infty }{\lim }\left({\log }_{\frac{1}{2}}x\right)=-\infty$

A. 1.

B. 2.

C. 3.

D. 4.

Hiển thị đáp án

Đáp án: C

Giải thích:

Nếu $C=\sqrt{AB}$ với $AB>0$ thì $2\ln C=\ln \left|A\right|+\ln \left|B\right|$. Do đó (I) sai.

● Với $a>1$ thì $\left(a-1\right){\log }_{a}x\ge 0$

$\iff {\log }_{a}x\ge 0\iff x\ge 1$

● Với $0<a<1$ thì $\left(a-1\right){\log }_{a}x\ge 0$

$\iff {\log }_{a}x\le 0\iff x\ge 1$

Do đó (II) đúng.

Lấy lôgarit cơ số a hai vế của $M^{{\log }_{a}N}=N^{{\log }_{a}M}$, ta có

${\log }_a\left(M^{{\log }_{a}N}\right)={\log }_a\left(N^{{\log }_{a}M}\right)$

$\iff {\log }_{a}N.{\log }_{a}M={\log }_{a}M.{\log }_{a}N$ .

Do đó (III) đúng.

Ta có $\underset{x\to +\infty }{\lim }\left({\log }_{\frac{1}{2}}x\right)=\underset{x\to +\infty }{\lim }\left[-{\log }_{2}x\right]$

$=-\underset{x\to +\infty }{\lim }\left({\log }_{2}x\right)=-\infty$

Do đó (IV) đúng.

Vậy ta có các mệnh đề (II), (III) và (IV) đúng.

Câu 3. Điều kiện để ${\log }_{a}b$ có nghĩa là:

A. $a<0,b>0$

B. $0<a\ne 1,b<0$

C. $0<a\ne 1,b>0$

D. $0<a\ne 1,0<b\ne 1$

Hiển thị đáp án

Đáp án: C

Giải thích:

Điều kiện để ${\log }_{a}b$ có nghĩa là: $0<a\ne 1,b>0$

Câu 4. Điều kiện để biểu thức ${\log }_2\left(3-x\right)$ xác định là:

A. $x\le 3$

B. $x>3$

C. $x\ge 3$

D. $x<3$

Hiển thị đáp án

Đáp án: D

Giải thích:

Để biểu thức ${\log }_2\left(3-x\right)$ xác định thì $3-x>0\iff x<3$

Câu 5. Cho hàm số $f\left(x\right)={\left(x^{1+\frac{1}{2{\log }_{4}x}}+8^{\frac{1}{3{\log }_{x^2}2}}+1\right)}^{\frac{1}{2}}-1$ với $0<x\ne 1$. Tính giá trị biểu thức $P=f\left(f\left(2017\right)\right).$

A. $P=2016.$

B. $P=1009.$

C. $P=2017.$

D. $P=1008.$

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có

$\begin{array}{l}{x}^{1+\frac{1}{2{\log }_{4}x}}=x^{1+\frac{1}{{\log }_{2}x}}\\ \end{array}$

$=x^{1+{\log }_{x}2}=x^{{\log }_x\left(2x\right)}=2x$

$8^{\frac{1}{3{\log }_{x^2}2}}=2^{3.\frac{1}{3.{\log }_{x^2}2}}$

$=2^{\frac{1}{{\log }_{x^2}2}}=2^{{\log }_2{x}^2}=x^2$

Khi đó $f\left(x\right)={\left(x^2+2x+1\right)}^{\frac{1}{2}}-1$

$={\left[{\left(x+1\right)}^2\right]}^{\frac{1}{2}}-1=x.$

Suy ra $f\left(2017\right)=2017$

$\stackrel{}{\to }f\left(f\left(2017\right)\right)=f\left(2017\right)=2017.$

Câu 6. Với điều kiện các logarit đều có nghĩa, chọn mệnh đề đúng?

A. ${\log }_a\left(bc\right)={\log }_{a}b+{\log }_{b}c$

B. ${\log }_a\frac{b}{c}={\log }_{a}b+{\log }_{a}c$

C. ${\log }_a\frac{b}{c}=\frac{{\log }_{a}b}{{\log }_{a}c}$

D. ${\log }_a\left(bc\right)={\log }_{a}b+{\log }_{a}c$

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có: ${\log }_a\left(bc\right)={\log }_{a}b+{\log }_{a}c$$\left(0<a\ne 1;b,c>0\right)$

${\log }_a\left(\frac{b}{c}\right)={\log }_{a}b-{\log }_{a}c$$\left(0<a\ne 1;b,c>0\right)$

Câu 7. Nếu a > 1 và b > c > 0 thì:

A. ${\log }_{a}b>{\log }_{a}c$

B. ${\log }_{a}b<{\log }_{a}c$

C. ${\log }_{a}b<{\log }_{b}c$

D. ${\log }_{a}b>{\log }_{c}b$

Hiển thị đáp án

Đáp án: A

Giải thích:

Nếu a > 1 và b > c > 0 thì ${\log }_{a}b>{\log }_{a}c$

Câu 8. Cho $a,b$ là các số thực dương khác 1 và thỏa mãn $ab\ne 1.$ Rút gọn biểu thức $P=\left({\log }_{a}b+{\log }_{b}a+2\right)\left({\log }_{a}b-{\log }_{ab}b\right){\log }_{b}a-1$.

A. $P={\log }_{b}a.$

B. $P=1.$

C. $P=0.$

D. $P={\log }_{a}b.$

Hiển thị đáp án

Đáp án: D

Giải thích:

Từ giả thiết, ta có

$P=\left({\log }_{a}b+{\log }_{b}a+2\right)$

$\times ({\log }_{a}b-\frac{1}{1+{\log }_{b}a}).{\log }_{b}a-1$

$\stackrel{t={\log }_{b}a}{\to }\left(t+\frac{1}{t}+2\right)\left(\frac{1}{t}-\frac{1}{t+1}\right)t-1$

$=\frac{{(t+1)}^2}{t}.\frac{1}{t(t+1)}t-1$

$=\frac{t+1}{t}-1=\frac{1}{t}={\log }_{a}b.$

Câu 9. Cho ba điểm $A\left(b;{\log }_{a}b\right),B\left(c;2{\log }_{a}c\right)$, $C\left(b;3{\log }_{a}b\right)$ với $0<a\ne 1,$ $b>0$. Biết B là trọng tâm của tam giác OAC với O là gốc tọa độ. Tính $S=2b+c.$

A. 9

B. 7

C. 11

D. 5

Hiển thị đáp án

Đáp án: A

Giải thích:

Vì B là trọng tâm của tam giác OAC nên

$\left\{\begin{array}{l}\frac{0+b+b}{3}=c\\ \frac{0+{\log }_{a}b+3{\log }_{a}b}{3}=2{\log }_{a}c\end{array}\right.$

$\iff \left\{\begin{array}{l}b+b=3c\\ 4{\log }_{a}b=6{\log }_{a}c\end{array}\right.$

$\iff \{\begin{array}{l}2b=3c\\ 2{\log }_{a}b=3{\log }_{a}c\end{array}$

$\iff \{\begin{array}{l}2b=3c\\ {\log }_a{b}^2={\log }_a{c}^3\end{array}$

$\iff \left\{\begin{array}{l}2b=3c\\ b^2=c^3\end{array}\right.$

$\stackrel{c>0}{\to }\{\begin{array}{l}b=\frac{27}{8}\\ c=\frac{9}{4}\end{array}$

$\stackrel{}{\to }S=2b+c=9.$

Câu 10. Cho a là số thực dương khác 4. Tính $I={\log }_{\frac{a}{4}}\left(\frac{a^3}{64}\right)$

A. $I=3$

B. $I=\frac{1}{3}$

C. $I=-\frac{1}{3}$

D. $I=-3$

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có: $I={\log }_{\frac{a}{4}}\left(\frac{a^3}{64}\right)$

$={\log }_{\frac{a}{4}}{\left(\frac{a}{4}\right)}^3$

$=3{\log }_{\frac{a}{4}}\frac{a}{4}=3$

Câu 11. Với điều kiện các biểu thức đều có nghĩa, chọn đẳng thức đúng:

A. ${\log }_{a^n}b={\log }_{b^n}a$

B. ${\log }_{a^n}b=\frac{1}{{\log }_{b^n}a}$

C. ${\log }_{a^n}b={\log }_a\sqrt[n]{b}$

D. ${\log }_{a^n}b=n{\log }_{b^n}a$

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có:

${\log }_{a^n}b=\frac{1}{n}{\log }_{a}b;$

${\log }_a\sqrt[n]{b}=\frac{1}{n}{\log }_{a}b$ nên ${\log }_{a^n}b={\log }_a\sqrt[n]{b}$ (C đúng)

Mặt khác: ${\log }_{a^n}b=\frac{1}{n}{\log }_{a}b;$

${\log }_{b^n}a=\frac{1}{n}{\log }_{b}a$ nên các đáp án A, B, D đều sai.

Câu 12. Cho $a,b,c$ là các số thực dương thỏa mãn $a^2=bc.$ Tính $S=2\ln a-\ln b-\ln c$.

A. $S=2\ln \left(\frac{a}{bc}\right).$

B. $S=1.$

C. $S=-2\ln \left(\frac{a}{bc}\right).$

D. $S=0.$

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có $S=2\ln a-\left(\ln b+\ln c\right)$

$=\ln a^2-\ln \left(bc\right)$

$=\ln \left(bc\right)-\ln \left(bc\right)=0.$

Câu 13. Cho $M={\log }_{12}x={\log }_{3}y$ với $x>0,y>0.$ Mệnh đề nào sau đây là đúng?

A. $M={\log }_4\left(\frac{x}{y}\right)$.

B. $M={\log }_{36}\left(\frac{x}{y}\right)$.

C. $M={\log }_9\left(x-y\right).$

D. $M={\log }_{15}\left(x+y\right)$.

Hiển thị đáp án

Đáp án: A

Giải thích:

Từ $M={\log }_{12}x={\log }_{3}y$

$\to \left\{\begin{array}{l}x={12}^M\\ y=3^M\end{array}\right.$

$\to \frac{x}{y}=4^M$

$\stackrel{}{\to }M={\log }_4\left(\frac{x}{y}\right).$

Cách trắc nghiệm.

● Cho $x=12\stackrel{}{\to }y=3$. Khi đó $M=1.$

Thử $x=12;y=3$ vào các đáp án thì có các đáp án A, C, D đều thỏa. Ta chưa kết luận được.

● Cho $x={12}^2\stackrel{}{\to }y=3^2$. Khi đó $M=2$.

Thử $x=144;y=9$ vào các đáp án thì có các đáp án A thỏa.

Câu 14. Cho là các số thực dương khác 1 và thỏa ${\log }_a{b}^2=x,{\log }_{b^2}\sqrt{c}=y$. Tính giá trị của biểu thức $P={\log }_{c}a.$

A. $P=\frac{2}{xy}.$

B. $P=2xy.$

C. $P=\frac{1}{2xy}.$

D. $P=\frac{xy}{2}.$

Hiển thị đáp án

Đáp án: C

Giải thích:

Nhận thấy các đáp án đều có tích xy nên ta sẽ tính tích này.

Ta có $xy={\log }_a{b}^2.{\log }_{b^2}\sqrt{c}$

$={\log }_a\sqrt{c}=\frac{1}{2}{\log }_{a}c$

$=\frac{1}{2{\log }_{c}a}$

$\stackrel{}{\to }{\log }_{c}a=\frac{1}{2xy}.$

Câu 15. Cho là các số thực dương khác 1 và $n\in {\mathbb{N}}^{\ast }$. Một học sinh tính $P=\frac{1}{{\log }_{a}b}+\frac{1}{{\log }_{a^2}b}+\mathrm{...}+\frac{1}{{\log }_{a^n}b}$ theo các bước sau:

I). $P={\log }_{b}a+{\log }_b{a}^2+\mathrm{...}+{\log }_b{a}^n$

II). $P={\log }_b\left(a^1{a}^2{a}^3\mathrm{...}{a}^n\right)$

III). $P={\log }_b{a}^{1+2+3+\mathrm{...}+n}$

IV). $P=n\left(n+1\right){\log }_{b}a$

Trong các bước trình bày, học sinh đã trình bày sai ở bước nào?

A. I.

B. II.

C. III.

D. IV.

Hiển thị đáp án

Đáp án: D

Giải thích:

Vì $P={\log }_b{a}^{1+2+3+\mathrm{...}+n}$

$=\left(1+2+3+\mathrm{...}+n\right).{\log }_{b}a$

$=\frac{n\left(n+1\right)}{2}.{\log }_{b}a$

Câu 16. Cho a, b là các số thực dương, thỏa mãn $a^{\frac{3}{4}}>a^{\frac{4}{5}}$ và ${\log }_b\frac{1}{2}<{\log }_b\frac{2}{3}$. Mệnh đề nào dưới đây đúng?

A. $a>1,0<b<1$

B. $0<a<1,0<b<1$

C. $0<a<1,b>1$

D. $a>1,b>1$

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có: $\frac{3}{4}<\frac{4}{5}$ và $a^{\frac{3}{4}}>a^{\frac{4}{5}}\Rightarrow 0<a<1$

$\frac{1}{2}<\frac{2}{3}$ và ${\log }_b\frac{1}{2}<{\log }_b\frac{2}{3}\Rightarrow b>1$

Câu 17. Cho $M=\frac{1}{{\log }_{a}x}+\frac{1}{{\log }_{a^2}x}+\mathrm{...}+\frac{1}{{\log }_{a^k}x}$ với $0<a\ne 1$ và $0<x\ne 1$. Mệnh đề nào sau đây là đúng?

A. $M=\frac{k\left(k+1\right)}{{\log }_{a}x}$.

B. $M=\frac{4k\left(k+1\right)}{{\log }_{a}x}$.

C. $M=\frac{k\left(k+1\right)}{2{\log }_{a}x}$.

D. $M=\frac{k\left(k+1\right)}{3{\log }_{a}x}$.

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có $M=\frac{1}{{\log }_{a}x}+\frac{1}{\frac{1}{2}{\log }_{a}x}+\frac{1}{\frac{1}{3}{\log }_{a}x}+\mathrm{...}+\frac{1}{\frac{1}{k}{\log }_{a}x}$

$=\frac{1}{{\log }_{a}x}+\frac{2}{{\log }_{a}x}+\frac{3}{{\log }_{a}x}+\mathrm{...}+\frac{k}{{\log }_{a}x}$

$=\frac{1}{{\log }_{a}x}.\left(1+2+3+\mathrm{...}+k\right)$

$=\frac{1}{{\log }_{a}x}.\frac{k(k+1)}{2}.$

Câu 18. Tính $P=\frac{1}{{\log }_{2}2017!}+\frac{1}{{\log }_{3}2017!}+\mathrm{...}+\frac{1}{{\log }_{2017}2017!}.$

A. $P=2017.$

B. $P=1.$

C. $P=0.$

D. $P=2017!.$

Hiển thị đáp án

Đáp án: B

Giải thích:

Áp dụng công thức ${\log }_{a}b=\frac{1}{{\log }_{b}a}$, ta được:

$P={\log }_{2017!}2+{\log }_{2017!}3+\mathrm{...}+{\log }_{2017!}2017$

$={\log }_{2017!}\left(\mathrm{2.3.4....2017}\right)$

$={\log }_{2017!}2017!=1.$

Câu 19. Đặt $a=\ln 3,b=\ln 5.$ Tính $I=\ln \frac{3}{4}+\ln \frac{4}{5}+\ln \frac{5}{6}+\mathrm{...}+\ln \frac{124}{125}$ theo a và b

A. $I=a-2b.$

B. $I=a+3b.$

C. $I=a+2b.$

D. $I=a-3b.$

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có $I=\ln \left(\frac{3}{4}.\frac{4}{5}.\frac{5}{6}\mathrm{...}\frac{124}{125}\right)$

$=\ln \frac{3}{125}=\ln 3-\ln 125$

$=\ln 3-3\ln 5=a-3b.$

Câu 20. Tính $P=\ln \left(2\cos 1^0\right).\ln \left(2\cos 2^0\right).\mathrm{...}\ln \left(2\cos {89}^0\right)$, biết rằng trong tích đã cho có 89 thừa số có dạng $\ln \left(2\cos a^0\right)$ với $1\le a\le 89$ và $a\in \mathbb{Z}$.

A. $P=1$.

B. $P=-1$.

C. $P=\frac{2^{89}}{89!}$.

D. $P=0$.

Hiển thị đáp án

Đáp án: D

Giải thích:

Trong tích trên có $\ln \left(2\cos {60}^0\right)=\ln \left(2.\frac{1}{2}\right)=\ln 1=0$

Vậy $P=0$.

Câu 21. Cho hàm số $f\left(x\right)=\frac{1}{2}{\log }_2\left(\frac{2x}{1-x}\right)$. Tính tổng $S=f\left(\frac{1}{2017}\right)+f\left(\frac{2}{2017}\right)+\mathrm{...}+f\left(\frac{2016}{2017}\right).$

A. $S=2016.$

B. $S=1008.$

C. $S=2017.$

D. $S=4032.$

Hiển thị đáp án

Đáp án: B

Giải thích:

Xét $f\left(x\right)+f\left(1-x\right)$

$=\frac{1}{2}{\log }_2\left(\frac{2x}{1-x}\right)+\frac{1}{2}{\log }_2\left[\frac{2\left(1-x\right)}{1-\left(1-x\right)}\right]$

$=\frac{1}{2}{\log }_2\left(\frac{2x}{1-x}\right)+\frac{1}{2}{\log }_2\left[\frac{2\left(1-x\right)}{x}\right]$

$=\frac{1}{2}{\log }_2[\frac{2x}{1-x}.\frac{2\left(1-x\right)}{x}]$

$=\frac{1}{2}{\log }_{2}4=1$

Áp dụng tính chất trên, ta được

$S=\left[f\left(\frac{1}{2017}\right)+f\left(\frac{2016}{2017}\right)\right]+\mathrm{...}+\left[f\left(\frac{1008}{2017}\right)+f\left(\frac{1009}{2017}\right)\right]$

$=1+1+\mathrm{...}+1=1008.$

Câu 22. Đặt $a={\log }_{2}5$ và $b={\log }_{2}6$. Hãy biểu diễn ${\log }_{3}90$ theo a và b?

A. ${\log }_{3}90=\frac{a-2b+1}{b+1}$

B. ${\log }_{3}90=\frac{a+2b-1}{b-1}$

C. ${\log }_{3}90=\frac{2a-b+1}{a+1}$

D. ${\log }_{3}90=\frac{2a+b-1}{a-1}$

Hiển thị đáp án

Đáp án: B

Giải thích:

Có: $b={\log }_{2}6=1+{\log }_{2}3$

$\Rightarrow {\log }_{2}3=b-1$

${\log }_{3}90={\log }_3\left(3^2\mathrm{.2.5}\right)$

$=2+{\log }_{3}2+{\log }_{3}5$

$=2+\frac{1}{{\log }_{2}3}+\frac{{\log }_{2}5}{{\log }_{2}3}$

$=2+\frac{1+{\log }_{2}5}{{\log }_{2}3}$

$=2+\frac{1+a}{b-1}$

$=\frac{a+2b-1}{b-1}$

Câu 23. Cho các số a, b, c thỏa mãn $\log {}_{a}3=2,{\log }_{b}3=\frac{1}{4},{\log }_{abc}3=\frac{2}{15}$. Giá trị của ${\log }_{c}3$ bằng:

A. 2

B. $\frac{1}{2}$

C. 3

D. $\frac{1}{3}$

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có:

$\left\{\begin{array}{c}{\log }_{a}3=2\\ {\log }_{b}3=\frac{1}{4}\end{array}\right.$

$\iff \left\{\begin{array}{c}\frac{1}{{\log }_{3}a}=2\\ \frac{1}{{\log }_{3}b}=\frac{1}{4}\end{array}\right.$

$\iff \left\{\begin{array}{c}{\log }_{3}a=\frac{1}{2}\\ {\log }_{3}b=4\end{array}\right.$

Tiếp tục có: ${\log }_{abc}3=\frac{2}{15}$ $\iff {\log }_3\left(abc\right)=\frac{15}{2}$

$\iff {\log }_{3}a+{\log }_{3}b+{\log }_{3}c=\frac{15}{2}$

$\iff \frac{1}{2}+4+{\log }_{3}c=\frac{15}{2}$

$\iff {\log }_{3}c=3$

$\iff {\log }_{c}3=\frac{1}{3}$

Câu 24. Xét a và b là hai số thực dương tùy ý. Đặt $x=\ln {\left(a^2-ab+b^2\right)}^{1000},$$y=1000\ln a-\ln \frac{1}{b^{1000}}$. Khẳng định nào dưới đây là khẳng định đúng?

A. $x<y$

B. $x>y$

C. $x\le y$

D. $x\ge y$

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có: $x=\ln {\left(a^2-ab+b^2\right)}^{1000}$

$=1000\ln \left(a^2-ab+b^2\right)$

$y=1000\ln a-\ln \frac{1}{b^{1000}}$

$=1000\ln a+1000\ln b$

$=1000\ln ab$

Ta có: $a^2-ab+b^2\ge ab$

$\Rightarrow \ln \left(a^2-ab+b^2\right)\ge \ln ab$

$1000\ln \left(a^2-ab+b^2\right)\ge 1000\ln ab$

$\iff x\ge y$

Câu 25. Cho $\ln x=2$. Tính giá trị của biểu thức $T=2\ln \sqrt{ex}-\ln \frac{e^2}{\sqrt{x}}+\ln 3.{\log }_{3}e{x}^2$?

A. T = 7

B. T = 12

C. T = 13

D. T = 21

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có:

$T=2\ln \sqrt{ex}-\ln \frac{e^2}{\sqrt{x}}+\ln 3.{\log }_{3}e{x}^2$

$=2\ln \left(e^{\frac{1}{2}}.x^{\frac{1}{2}}\right)-\left(\ln e^2-\ln x^{\frac{1}{2}}\right)+\ln 3.\frac{\ln \left(e.x^2\right)}{\ln 3}$

$=2\left(\frac{1}{2}+\frac{1}{2}\ln x\right)-\left(2-\frac{1}{2}\ln x\right)+\ln e+2\ln x$

$=2\left(\frac{1}{2}+\frac{1}{2}.2\right)-\left(2-\frac{1}{2}.2\right)+1+2.2=7$

Câu 26. Cho ${\log }_{2}x=\sqrt{2}$. Tính giá trị biểu thức $P={\log }_2{x}^2+{\log }_{\frac{1}{2}}{x}^3+{\log }_{4}x.$

A. $P=\frac{11\sqrt{2}}{2}.$

B. $P=\sqrt{2}$.

C. $P=-\frac{\sqrt{2}}{2}.$

D. $P=3\sqrt{2}.$

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có $P=2{\log }_{2}x-3{\log }_{2}x+\frac{1}{2}{\log }_{2}x$

$=-\frac{1}{2}{\log }_{2}x=-\frac{1}{2}.\sqrt{2}$

$=-\frac{\sqrt{2}}{2}$

Câu 27. Cho $a={\log }_{2}m$ và $A={\log }_{m}8m$, với $0<m\ne 1$. Mệnh đề nào sau đây đúng?

A. $A=\left(3-a\right)a.$

B. $A=\left(3+a\right)a.$

C. $A=\frac{3-a}{a}.$

D. $A=\frac{3-a}{a}.$

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có $A={\log }_{m}8m={\log }_{m}8+{\log }_{m}m$

$=3{\log }_{m}2+1=\frac{3}{{\log }_{2}m}+1$

$=\frac{3}{a}+1=\frac{3+a}{a}.$

Câu 28. (ĐỀ CHÍNH THỨC 2016 – 2017) Với các số thực dương $x,y$ tùy ý, đặt ${\log }_{3}x=a$ và ${\log }_{3}y=b$. Mệnh đề nào sau đây là đúng ?

A. ${\log }_{27}{\left(\frac{\sqrt{x}}{y}\right)}^3=\frac{a}{2}+b.$

B. ${\log }_{27}{\left(\frac{\sqrt{x}}{y}\right)}^3=\frac{a}{2}-b.$

C. ${\log }_{27}{\left(\frac{\sqrt{x}}{y}\right)}^3=9\left(\frac{a}{2}+b\right).$

D. ${\log }_{27}{\left(\frac{\sqrt{x}}{y}\right)}^3=9\left(\frac{a}{2}-b\right).$

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có ${\log }_{27}{\left(\frac{\sqrt{x}}{y}\right)}^3=\frac{3}{3}{\log }_3\left(\frac{\sqrt{x}}{y}\right)$

$={\log }_3\sqrt{x}-{\log }_{3}y$

$=\frac{1}{2}{\log }_{3}x-{\log }_{3}y=\frac{a}{2}-b.$

Câu 29. Cho ${\log }_{2}5=a,{\log }_{3}5=b$. Tính giá trị biểu thức $A=\frac{{\log }_{5}120}{2^{{\log }_4\sqrt{2}}}$ theo a và b.

A. $A=\frac{2b+ab+a}{\sqrt[4]{2}ab}$.

B. $A=\frac{3b+ab+a}{ab}$.

C. $A=\frac{3b+ab+a}{\sqrt[4]{2}ab}$.

D. $A=\frac{b+ab+3a}{\sqrt[4]{2}ab}$.

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có $A=\frac{{\log }_{5}120}{2^{{\log }_4\sqrt{2}}}=\frac{{\log }_5\left(2^3\mathrm{.5.3}\right)}{2^{\frac{1}{4}}}$

$=\frac{3{\log }_{5}2+1+{\log }_{5}3}{\sqrt[4]{2}}$

$=\frac{\frac{3}{a}+1+\frac{1}{b}}{\sqrt[4]{2}}=\frac{3b+ab+a}{\sqrt[4]{2}ab}.$

Chọn C.

Cách 2. Dùng CASIO:

Bấm máy ${\log }_{2}5$ và lưu vào biến A; Bấm máy ${\log }_{3}5$ và lưu vào biến B.

Giả sử với đáp án A, nếu đúng thì hiệu $\frac{{\log }_{5}120}{2^{{\log }_4\sqrt{2}}}-\frac{2b+ab+a}{\sqrt[4]{2}ab}$ phải bằng 0.

Nhập vào màn hình $\frac{{\log }_{5}120}{2^{{\log }_4\sqrt{2}}}-\frac{2\text{B}+\text{AB}+\text{A}}{\sqrt[4]{2}\text{AB}}$ với A, B là các biến đã lưu và nhấn dấu =.

Màn hình xuất hiện số khác 0. Do đó đáp án A không thỏa mãn.

Thử lần lượt và ta chọn được đáp án đúng là C.

Câu 30. (ĐỀ MINH HỌA 2016 – 2017) Đặt $a={\log }_{2}3$ và $b={\log }_{5}3$. Hãy biểu diễn ${\log }_{6}45$ theo a và b.

A. ${\log }_{6}45=\frac{a+2ab}{ab}$.

B. ${\log }_{6}45=\frac{2a^2-2ab}{ab}$.

C. ${\log }_{6}45=\frac{a+2ab}{ab+b}$.

D. ${\log }_{6}45=\frac{2a^2-2ab}{ab+b}$.

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có ${\log }_{6}45={\log }_{6}9+{\log }_{6}5.$

${\log }_{6}9=2{\log }_{6}3$

$=\frac{2}{{\log }_{3}6}=\frac{2}{1+{\log }_{3}2}$

$=\frac{2}{1+\frac{1}{a}}=\frac{2a}{a+1}.$

${\log }_{6}5=\frac{1}{{\log }_{5}6}$

$=\frac{1}{{\log }_{5}3+{\log }_{5}2}$

$=\frac{a}{b\left(a+1\right)}$ vì ${\log }_{5}2=\frac{b}{a}$

Vậy ${\log }_{6}45=\frac{2a}{a+1}+\frac{a}{b\left(a+1\right)}$

$=\frac{a+2ab}{ab+b}.$

Câu 31. Biết 3 + 2log₂x = log₂y . Hãy biểu thị y theo x

A. y = 2x+3

B. y = 8x²

C. y = x²+8

D. y = 3x²

Hiển thị đáp án

Đáp án: B

Giải thích:

3 + 2log₂x = log₂y ⇔ log₂2³ + log₂x² = log₂y

Chọn đáp án B

Câu 32. Nếu x = (log₈2)^log₂8 thì log₃x bằng:

A. -3

B. -1/3

C. 1/3

D. 3

Hiển thị đáp án

Đáp án: A

Giải thích:

x = (log₈2)^log₂8 = (log_2³2)^log₂23 = (1/3)³ = 3^-3 => log₃x = -3

Câu 33. Độ pH của một chất được xác định bởi công thức pH = -log[H⁺] trong đó [H⁺] là nồng độ ion hyđrô trong chất đó tính theo mol/lít (mol/L). Xác định nồng độ ion H⁺ của một chất biết rằng độ pH của nó là 2,44

A. 1,1.108 mol/L

B. 3,2.10-4 mol/L

C. 3,6.10-3 mol/L

D. 3,7.10-3 mol/L

Hiển thị đáp án

Đáp án: C

Giải thích:

pH = -log[H⁺]

=> [H⁺] = 10^-pH = 10^-2,44 ≈ 0,00363 ≈ 3,6.10^-3 (mol/L).

Câu 34. Tính giá trị biểu thức

A. 0,01

B. 0,1

C. 1

D. 10

Hiển thị đáp án

Đáp án: C

Giải thích:

Biểu thức đã cho bằng

log_100!2 + log_100!3 + log_100!4 + ... + log_100!100 = log_100!(2.3.4....10) = log_100!100! = 1

Câu 35. Tính giá trị của biểu thức log₃100 - log₃18 - log₃50

A. -3

B. -2

C. 2

D. 3

Hiển thị đáp án

Đáp án: B

Giải thích:

log₃100 - log₃18 - log₃50

Câu 36. Tính giá trị của biểu thức (log₂3)(log₉4)

A. 2/3

B. 1

C. 3/2

D. 4

Hiển thị đáp án

Đáp án: B

Giải thích:(log₂3)(log₉4) = (log₂3) = (log_3²2²) = (log₂3)(log₃2) = 1

Câu 37. 10^log7 bằng:

A. 1

B. log₇10

C. 7

D. log7

Hiển thị đáp án

Đáp án: C

Giải thích:

Sử dụng công thức a^log_ab

⇒ 10^log7 = 7

Câu 38. Cho P = log₃(a²b³) (a,b là các số dương). Khẳng định nào sau đây là đúng ?

A. P = 6log₃a.log₃b

B. P = 2log₃a + 3log₃b

C. P = (1/2)log₃a + (1/3)log₃b

D. P = (log₃a)².(log₃b)³

Hiển thị đáp án

Đáp án: B

Giải thích:

P = log₃a² + log₃b³ = 2log₃a + 3log₃b

Câu 39. Đặt a = log₂7, b = log₂3. Tính log₂(56/9) theo a và b

A. P = 3 + a - 2b

B. P = 3 + a - b²

C. P = 3a/2b

D. 3a/b²

Hiển thị đáp án

Đáp án: A

Giải thích:

P = log₂56 - log₂9 = log₂(8.7) - log₂3²

= log₂2³ + log₂7 - 2log₂3 = 3 + log₂7 - 2log₂3 = 3 + a - 2b

Câu 40. Biết rằng 4^a = 5, 5^b = 6, 6^c = 7, 7^d = 8. Tính abcd

A. 1/2

B. 3/2

C. 2

D. 2/3

Hiển thị đáp án

Đáp án: B

Giải thích:

Từ giả thiết ta có: a = log₄5, b = log₅6, c = log₆7, d = log₇8

=> abcd = log₄5.log₅6.log₆7.log₇8 = log₄6log₆7log₇8 = log₄7.log₇8 = log₄8 = log_2²2³ = (3/2)log₂2 = 3/2

Các câu hỏi trắc nghiệm Toán lớp 12 có đáp án, chọn lọc khác:

Trắc nghiệm Hàm số mũ. Hàm số Logarit có đáp án

Trắc nghiệm Phương trình mũ và phương trình Logarit có đáp án

Trắc nghiệm Bất phương trình mũ và bất phương trình Logarit có đáp án

Trắc nghiệm Ôn tập Chương 2 có đáp án

Trắc nghiệm Nguyên hàm có đáp án