TOP 40 câu Trắc nghiệm Ôn tập Chương 2: Mặt nón. Mặt trụ. Mặt cầu (có đáp án 2024) - Toán 12
Bộ 40 câu hỏi trắc nghiệm Toán lớp 12 Bài: Ôn tập Chương 2 - Mặt nón. Mặt trụ. Mặt cầu có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 12 Bài Ôn tập chương 2.
Trắc nghiệm Toán 12 Bài: Ôn tập Chương 2
Câu 1. Cho các hình sau đây: điểm, đường thẳng, đường tròn. Số hình khi quay quanh một trục cố định ta được mặt tròn xoay là:
A. 1
B. 2
C. 3
D. 0
Đáp án: B
Giải thích:
Khi quay đường thẳng, đường tròn quanh một trục cố định thì ta được mặt tròn xoay.
Khi quay một điểm quanh trục cố định ta chỉ được một đường tròn.
Câu 2. Quay đường cong nào sau đây quanh trục đối xứng của nó ta sẽ được một mặt cầu?
A. Elip
B. Parabol
C. Đường tròn
D. Nửa đường tròn
Đáp án: C
Giải thích:
Đáp án A: quay elip quanh trục đối xứng của nó ta được mặt tròn xoay nhưng không phải mặt cầu
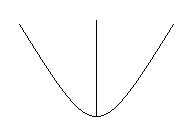
Đáp án B: quay parabol quanh trục đối xứng của nó ta được mặt tròn xoay mà không phải mặt cầu.
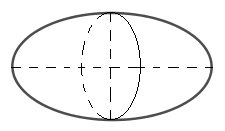
Đáp án C: quay đường tròn quanh đường kính của nó ta được mặt cầu.
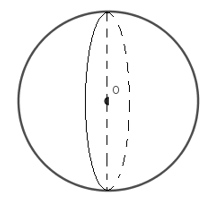
Đáp án D: quay nửa đường tròn quanh trục đối xứng của nó ta chỉ được nửa mặt cầu
Câu 3. Cho mặt cầu (S ) tâm O, bán kính R và mặt phẳng (P), gọi H là hình chiếu của O trên (P). Nếu R > OH thì:
A. (P) cắt (S)
B. (P) tiếp xúc (S)
C. (P) và (S) không có điểm chung
D. (P) cắt (S) tại hai điểm phân biệt
Đáp án: A
Giải thích:
Nếu OH < R thì (P) cắt (S) theo giao tuyến là một đường tròn
Câu 4. Cho mặt cầu (S) có tâm O bán kính R và đường thẳng d. Nếu d và (S) không có điểm chung thì:
A. d(O;d)>R
B. d(O;d)<R
C. d(O;d)=R
D. d(O;d)≤R
Đáp án: A
Giải thích:
Mặt cầu (S) và đường thẳng d không có điểm chung nếu d(O;d)>R
Câu 5. Cho hai đường thẳng d và d’ cắt nhau tại điểm O và góc giữa hai đường thẳng là α(0°<α<90°). Quay đường thẳng d’ quanh d thì ta được mặt nón có góc ở đỉnh bằng:
A. 2α
B. α
C. α2
D. 4α
Đáp án: A
Giải thích:
α là góc giữa hai đường thẳng d, d’ thì góc 2α là góc ở đỉnh của mặt nón.
Câu 6. Quay hình tam giác vuông ABC tại A có ˆB=30° quanh trục là đường thẳng AC ta được hình nón có góc ở đỉnh bằng:
A. 30°
B. 60°
C. 90°
D. 120°
Đáp án: D
Giải thích:
Quay hình tam giác vuông ABC tại A có ˆB=30° quanh trục là đường thẳng AC ta được hình nón đỉnh C có góc ở đỉnh ˆC=120°
Câu 7. Chọn mệnh đề sai:
A. Điểm không thuộc khối cầu thì không thuộc mặt cầu.
B. Điểm nằm ngoài mặt cầu thì không thuộc khối cầu.
C. Điểm không thuộc mặt cầu thì không thuộc khối cầu.
D. Điểm nằm trong mặt cầu thì thuộc khối cầu.
Đáp án: C
Giải thích:
Điểm không thuộc mặt cầu thì có thể nằm ngoài hoặc nằm trong mặt cầu nên các điểm nằm trong mặt cầu vẫn thuộc khối cầu.
Do đó C sai.
Câu 8. Chọn mệnh đề đúng:
A. Mặt phẳng cắt mặt cầu là mặt phẳng kính.
B. Mặt phẳng chứa đường kính của mặt cầu là mặt phẳng kính.
C. Mặt phẳng tiếp xúc với mặt cầu là mặt phẳng kính.
D. Mặt phẳng không đi qua điểm nao thuộc mặt cầu là mặt phẳng kính.
Đáp án: B
Giải thích:
Nếu (P) là mặt phẳng kính thì OH = 0 (H trùng O) hay (P) đi qua O là tâm mặt cầu, do đó (P) đi qua đường kính của mặt cầu.
Câu 9. Công thức tính bán kính mặt cầu ngoại tiếp hình chóp có cạnh bên vuông góc với đáy là:
A. R=√r2+h24
B. R=√r2+h22
C. R=√r2-h24
D. R=r2+h24
Đáp án: A
Giải thích:
Hình chóp có cạnh bên vuông góc với đáy nội tiếp mặt cầu có bán kính R=√r2+h24 với r là bán kính đường tròn đáy, h là chiều cao hình chóp (độ dài cạnh bên vuông góc với đáy)
Câu 10. Hình lập phương có độ dài cạnh a = 6 thì đường kính mặt cầu ngoại tiếp là:
A. 6
B. 6√2
C. 6√3
D. 6√6
Đáp án: C
Giải thích:
Đường kính mặt cầu ngoại tiếp hình lập phương cạnh a là
D=2R=a√3=6√3
Câu 11. Trục đa giác đáy là đường thẳng vuông góc với mặt phẳng đáy tại:
A. Đỉnh đa giác đáy.
B. Trực tâm đa giác đáy
C. Trọng tâm đa giác đáy
D. Tâm đường tròn đáy
Đáp án: D
Giải thích:
Trục đa giác đáy: là đường thẳng đi qua tâm đường tròn ngoại tiếp đa giác đáy và vuông góc với mặt phẳng chứa đa giác đáy.
Câu 12. Trong không gian, tập hợp các điểm cách đều hai đầu mút của đoạn thẳng là:
A. Đường trung trực của đoạn thẳng
B. Trung điểm của đoạn thẳng
C. Mặt phẳng trung trực của đoạn thẳng
D. Đường tròn đường kính là đoạn thẳng đó.
Đáp án: C
Giải thích:
Mọi điểm nằm trên mặt phẳng trung trực của đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng và ngược lại
Câu 13. Cho hình nón có các kích thước r=1cm, l=2cm với r, l lần lượt là bán kính đáy và độ dài đường sinh hình nón. Diện tích toàn phần hình nón là:
A. 2π(cm2)
B. 4π(cm2)
C. 3π(cm2)
D. 6π(cm2)
Đáp án: C
Giải thích:
Áp dụng công thức : Stp=πrl+πr2 ta được:
Stp=πrl+πr2
=π.1.2+π.12=3π(cm2)
Câu 14. Cho hình nón S có bán kính R=a√2, góc ở đỉnh bằng 60°. Diện tích toàn phần của hình nón bằng:
A. 8πa2
B. 6πa2
C. 2πa2
D. 4πa2
Đáp án: B
Giải thích:
Vì góc ở đỉnh bằng 60° nên thiết diện qua trục là tam giác đều cạnh 2R=2a√2, do đó độ dài đường sinh:
l=2R=2a√2
⇒Sxq=πRl=π.a√2.2a√2
=4πa2
Diện tích đáy: Sd=πR2=π(a√2)2=2πa2
Diện tích toàn phần:
Stp=Sxq+Sd
=4πa2+2πa2=6πa2
Câu 15. Công thức tính diện tích mặt cầu là:
A. S=πR2
B. S=4πR2
C. S=2πR2
D. S=34πR2
Đáp án: B
Giải thích:
Công thức tính diện tích mặt cầu: S=4πR2
Câu 16. Cho tam giác ABC vuông tại A, AH là đường cao. Khi quay các cạnh của tam giác ABC quanh cạnh BC thì số hình nón được tạo thành là mấy hình?
A. 1
B. 0
C. 3
D. 2
Đáp án: D
Giải thích:
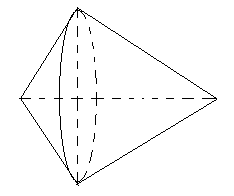
Quay tam giác vuông ABC quanh cạnh huyền BC ta được hai hình nón.
Câu 17. Diện tích xung quanh của hình nón có bán kính đường tròn đáy R và chiều cao h bằng:
A. Sxq=13πR2h
B. Sxq=πR√R2+h2
C. Sxq=πR√R2−h2
D. Sxq=πRh
Đáp án: B
Giải thích:
Hình nón có bán kính đáy R và chiều cao h thì đường sinh l=√R2+h2
Khi đó diện tích xung quanh hình nón là: Sxq=πRl=πR√R2+h2
Câu 18. Cho hình vẽ sau, chọn mệnh đề sai:
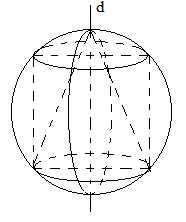
A. Mặt cầu ngoại tiếp hình nón
B. Hình nón nội tiếp hình trụ
C. Hình trụ nội tiếp mặt cầu
D. Hình nón nội tiếp mặt cầu
Đáp án: B
Giải thích:
Quan sát hình vẽ ta thấy hình trụ nội tiếp mặt cầu, hình nón nội tiếp mặt cầu, mặt cầu ngoại tiếp hình nón nên các đáp án A, C và D đúng.
Ngoài ra hình nón không nội tiếp hình trụ vì hình trụ không đi qua đỉnh hình nón.
Câu 19. Cho điểm M, đường tròn (CM) trục Δ và các điểm N∈(CM),A∈Δ. Chọn mệnh đề sai:
A. MN là đường kính
B. d(M,Δ)=d(N,Δ)
C. MN⊥Δ
D. AM=AN
Đáp án: A
Giải thích:
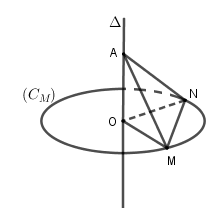
Đường tròn (CM) là đường tròn đi qua điểm M
Vì N∈(CM) nhưng MN chưa chắc là đường kính nên A sai.
Ngoài ra, d(M,Δ)=MO=NO=d(N,Δ)
Δ vuông góc với mp chứa (CM) nên vuông góc với mọi đường thẳng thuộc mp này.
Do đó MN⊥Δ
Tam giác vuông AOM = AON (hai cạnh góc vuông) nên AM = AN.
Vậy các đáp án còn lại đều đúng.
Câu 20. Cho hình nón tròn xoay có đường cao h = 40 cm, bán kính đáy r = 50 cm. một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là 24 cm. Tính diện tích của thiết diện
A. S=800(cm2)
B. S=1200(cm2)
C. S=1600(cm2)
D. S=2000(cm2)
Đáp án: D
Giải thích:
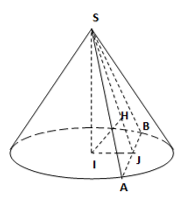
Gọi J là trung điểm của AB.
Có: {AB⊥IJAB⊥SI⇒AB⊥(SJI)
Nên: {(SAB)⊥(SIJ)(SAB)∩(SIJ)=SJIH⊥SJ
⇒d(I;(SAB))=IH=24
1IH2=1SI2+1IJ2
⇔1IJ2=−1402+1242
⇔IJ=30
Nên: BJ=√502−302=40
Và SJ=√402+302=50
Vậy SΔSAB=12SJ.AB
=12.50.80=2000(cm2)
Câu 21. Tính thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) quanh trục DF
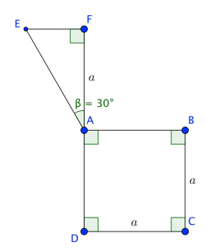
A. 10πa39
B. 10πa37
C. 5πa32
D. πa33
Đáp án: A
Giải thích:
Ta có: EF=AF.tanβ
=a.tan30°=a√33
Khi quay quanh trục DF, tam giác AEF tạo ra một hình nón có thể tích
V1=13π.EF2.AF
=13π.(a√33)2.a=πa39
Khi quay quanh trục DF, hình vuồn ABCD tạo ra một hình trụ có thể tích
V2=π.DC2.BC
=π.a2.a=πa3
Thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) quanh trục DF là:
V=V1+V2
=πa39+πa3=109πa3
Câu 22. Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông tại A, AB=2a√3. Đường chéo BC’ tạo với mặt phẳng (AA’C’C) một góc bằng 60°. Gọi (S) là mặt cầu ngoại tiếp hình lăng trụ đã cho. Bán kính của mặt cầu (S) bằng:
A. a2
B. a
C. 3a
D. 2a
Đáp án: D
Giải thích:
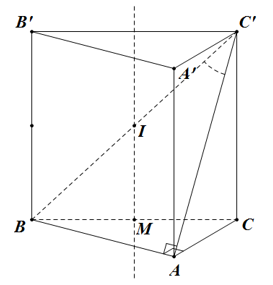
Gọi M là trung điểm BC, I là trung điểm BC’.
Khi đó, IM là trục của đường tròn ngoại tiếp tam giác ABC.
Mặt khác, IB=IC=IB'. Do dó, I là tâm mặt cầu ngoại tiếp lăng trụ ABC.A’B’C’
Bán kính
Câu 23. Cho hình lăng trụ tam giác đều ABC.A’B’C’ có độ dài cạnh đáy bằng a và chiều cao bằng h. Tính thể tích V của khối trụ ngoại tiếp lăng trụ đã cho.
A.
B.
C.
D.
Đáp án: B
Giải thích:
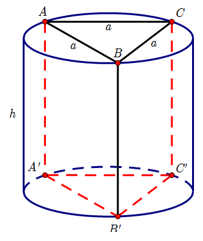
Khối trụ ngoại tiếp lăng trụ tam giác đều có hình tròn đáy là hình nón ngoại tiếp tam giác đáy của lăng trụ, và chiều cao bằng chiều cao lăng trụ.
Tam giác đều cạnh a có bán kính đương tròn ngoại tiếp bằng: .
Vậy thể tích của khối trụ cần tìm:
(đvtt)
Câu 24. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, , tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABC
A.
B.
C.
D.
Đáp án: C
Giải thích:
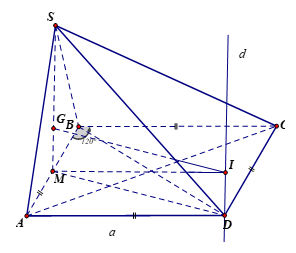
Do
đều.
nên D là tâm đường tròn ngoại tiếp
Gọi M là trung điểm của AB, G là trọng tâm của tam giác SAB.
Qua D kẻ và qua G kẻ
Gọi
Ta có:
Khi đó I là tâm của mặt cầu ngoại tiếp hình chóp S.ABC có bán kính
Câu 25. Cho hình hộp chữ nhật ABCD.A’B’C’D’ có đáy là hình vuông cạnh a và cạnh bên bằng 2a. Diện tích xung quanh của hình nón có đỉnh là tâm O của hình vuông A’B’C’D’ và đáy là hình tròn nội tiếp hình vuông ABCD là:
A.
B.
C.
D.
Đáp án: A
Giải thích:
Dựa vào giả thiết ta có bán kính đáy hình nón là bán kính đường tròn nội tiếp hình vuông nên
Chiều cao hình nón là khoảng cách từ O đến mp (ABCD) nên h = 2a.
Độ dài đường sinh hình nón là:
Diện tích xung quanh của hình nón là:
Câu 26. Cho điểm M, đường tròn trục và các điểm . Chọn mệnh đề sai:
A. MN là đường kính
B.
C.
D.
Đáp án: A
Giải thích:
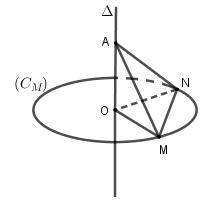
Đường tròn là đường tròn đi qua điểm M
Vì nhưng MN chưa chắc là đường kính nên E sai.
Ngoài ra,
vuông góc với mp chứa nên vuông góc với mọi đường thẳng thuộc mp này.
Do đó
Tam giác vuông AOM = AON (hai cạnh góc vuông) nên AM = AN.
Vậy các đáp án còn lại đều đúng.
Câu 27. Cho hình nón tròn xoay có đường cao h = 40 cm, bán kính đáy r = 50 cm. một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là 24 cm. Tính diện tích của thiết diện
A.
B.
C.
D.
Đáp án: D
Giải thích:
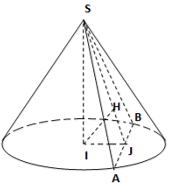
Gọi J là trung điểm của AB.
Có:
Nên:
Nên:
Và
Vậy
Câu 28. Người ta thả một viên billiards có dạng hình cầu với bán kính nhỏ hơn 4,5 cm vào một chiếc cốc hình trụ đang chứa nước thì viên billiards đó tiếp xúc với đáy cốc và tiếp xúc với mặt nước sau khi dâng (tham khảo hình vẽ bên). Biết rằng bán kính của phần trong đáy cốc bằng 5,4 cm và chiều cao của mực nước ban đầu trong cốc bằng 4,5 cm. Bán kính của viên billiards đó bằng:
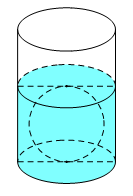
A. 4,2 cm
B. 3,6 cm
C. 2,6 cm
D. 2,7 cm
Đáp án: D
Giải thích:
Thể tích mực nước ban đầu là:
Gọi R là bán kính của viên bi ta có sau khi thả viên bi vào cốc, chiều cao của mực nước bằng 2R, do đó tổng thể tích của nước và bi sau khi thẻ viên bi vào trong cốc là:
Thể tích của quả cầu là:
Ta có:
Giải phương trình trên với điều kiện
Câu 29. Một hình nón đỉnh S có bán kính đáy bằng , góc ở đỉnh là . Thiết diện qua đỉnh của hình nón là một tam giác. Diện tích lớn nhất của thiết diện đó là bao nhiêu?
A.
B.
C.
D.
Đáp án: A
Giải thích:
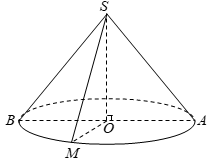
Giả sử O là tâm đáy và AB là một đường kính của đường tròn đáy hình nón.
Thiết diện qua đỉnh của hình nón là tam giác can SAM. Theo giả thiết hình nón có bán kính đáy
nên
Xét tam giác SOA vuông tại O, ta có
Diện tích thiết diện là
Do nên lớn nhất khi và chỉ khi hay khi tam giác ASM vuông cân đỉnh S (vì nên tồn tại tam giác ASM thỏa mãn)
Vậy diện tích thiết diện lớn nhất là: (đvdt)
Câu 30. Tính thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) quanh trục DF
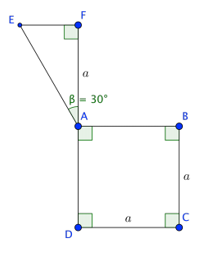
A.
B.
C.
D.
Đáp án: A
Giải thích:
Ta có:
Khi quay quanh trục DF, tam giác AEF tạo ra một hình nón có thể tích
Khi quay quanh trục DF, hình vuồn ABCD tạo ra một hình trụ có thể tích
Thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) quanh trục DF là:
Câu 31. Hình trụ (H) có diện tích xung quanh là 6π(cm2) và thể tích khối trụ là 9π(cm3). Chiều cao của hình lăng trụ là :
A. 1(cm)
B. 3(cm)
C. 1/2 (cm)
D. 2(cm)
Đáp án: A
Giải thích:
Từ giả thiết ta có:
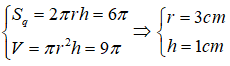
Câu 32. Cho hình nón tròn xoay có đường cao 12cm và đường kính đáy 10cm. Độ dài đường sinh của hình nón là :
A. √119 (cm)
B. 17(cm)
C. 15(cm)
D. 13(cm)
Đáp án: C
Giải thích:
Từ giả thiết ta có:
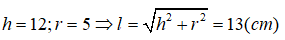
Câu 33. Cho hình nón tròn xoay có đỉnh là S, O là tâm của đường tròn đáy, đường sinh bằng a√2 và góc giữa đường sinh và mặt phẳng đáy bằng 60° . Diện tích xung quanh Sxq của hình nón và thể tích V của khối nón tương ứng là:
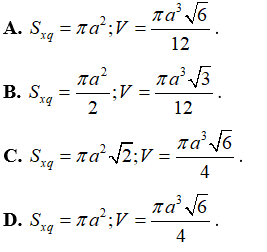
Đáp án: A
Giải thích:
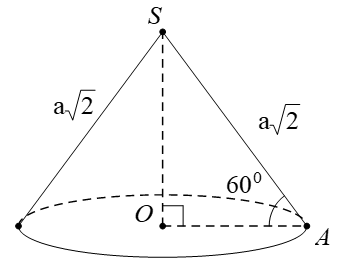
Gọi A là một điểm thuộc đường tròn đáy hình nón. Theo giải thiết ta có đường sinh SA = a√2 và góc giữa đường sinh và mặt phẳng đáy là 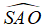
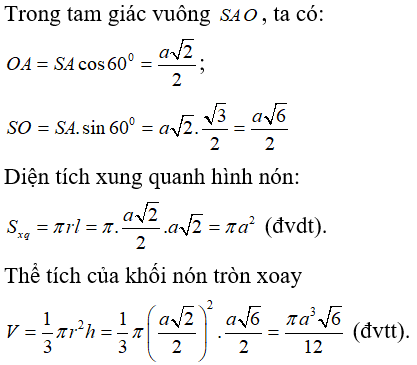
Câu 34. Một hình trụ có bán kính đáy bằng a và có thiết diện qua trục là một hình chữ nhật có diện tích là 2a2 . Diện tích xung quanh của hình trụ là :
A. 4πa2
B. 3πa2
C. 2πa2
D. πa2
Đáp án: C
Giải thích:
Từ giả thiết ta có: r = a; 2a.h = 2a2 => h = a => Sxq = 2πrh = 2πa2
Câu 35. Tính thể tích của khối trụ biết chu vi đáy của hình trụ đó bằng 6π (cm) và thiết diện đi qua trục là một hình chữ nhật có độ dài đường chéo bằng 10 (cm) .
A. 48π (cm3)
B. 24π (cm3)
C. 72π (cm3)
D. 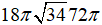 (cm3)
(cm3)
Đáp án: C
Giải thích:
Gọi O, O' là hai tâm của đáy hình trụ và thiết diện qua trục là hình chữ nhật ABCD .
Do chu vi đáy của hình trụ đó bằng 6π (cm) nên bán kính đáy của hình trụ là

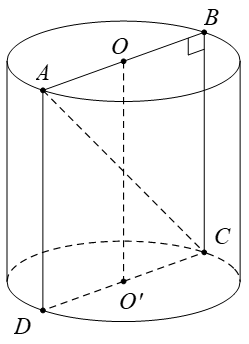
Câu 36. Cho khối trụ có diện tích toàn phần là 6πa2 và thể tích là 2πa3. Bán kính đáy của hình trụ là :
A. 3a/2
B. a
C. 2a/3
D. 2a
Đáp án: A
Giải thích:
Từ giả thiết ta có:
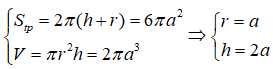
Câu 37. Cho hình chóp S.ABC có đáy ABC là tam giác vuông đỉnh A và BC = a. Cạnh bên SB vuông góc với mặt phẳng (ABC), SC tại với mặt phẳng (ABC) một góc là 60o. Bán kính mặt cầu ngoại tiếp hình chóp là :
A. a√3
B. a√2
C. a√3/2
D. a
Đáp án: D
Giải thích:
Ta có:
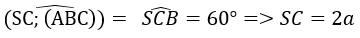
Gọi I là trung điểm của SC. Theo định lí ba đường vuông góc ta có tam giác SAC vuông tại A, mà tam giác SBC vuông tại B nên I cách đều các đỉnh của hình chóp hay I là tâm mặt cầu ngoại tiếp hình chóp. Khi đó ta có bán kính: r = SC/2 = a
Câu 38. Cho hình hộp chữ nhật ABCD.A'B'C'D' có AD = a; AB' = 2a. Diện tích mặt cầu ngoại tiếp tứ diện ACB’D’ là :
A. 5πa2
B. 3πa2
C. 5πa2/4
D. 5πa2/3
Đáp án: A
Giải thích:
Ta có mặt cầu ngoại tiếp tứ diện ACB’D’ cũng chính là mặt cầu ngoại tiếp hình hộp chữ nhật nên có bán kính
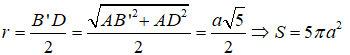
Câu 39. Cho hình nón đỉnh S với đáy là đường tròn tâm O bán kính R . Gọi I là một điểm nằm trên mặt phẳng đáy sao cho OI = R√3 . Giả sử A là điểm nằm trên đường tròn (O; R) sao cho OA ⊥ OI . Biết rằng tam giác SAI vuông cân tại S . Khi đó, diện tích xung quanh Sxq của hình nón và thể tích V của khối nón là:
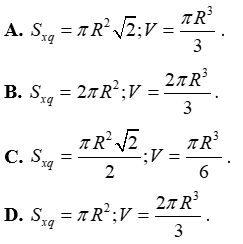
Đáp án: A
Giải thích:
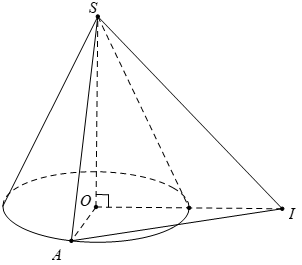

Câu 40. Một cái tháp khổng lồ có thân là hình trụ và mái là một nửa hình cầu. Người ta muốn sơn toàn bộ mặt ngoài của thắp (kể cả mái). Tính diện tích S cần sơn (làm tròn đến mét vuông).
A. S = 8243 (m2)
B. S = 11762 (m2)
C. S = 12667 (m2)
D. S = 23524 (m2)
Đáp án: A
Giải thích:

Các câu hỏi trắc nghiệm Toán lớp 12 có đáp án, chọn lọc khác:
Trắc nghiệm Hệ tọa độ trong không gian có đáp án
Trắc nghiệm Phương trình mặt phẳng có đáp án
Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án
Trắc nghiệm Ôn tập Chương 3 - Phương pháp tọa độ trong không gian có đáp án
Xem thêm các chương trình khác:
- Trắc nghiệm Sinh học lớp 7 có đáp án
- Trắc nghiệm Toán lớp 7 có đáp án
- Trắc nghiệm Ngữ văn lớp 7 có đáp án
- Trắc nghiệm Sinh học 8 có đáp án
- Trắc nghiệm Toán lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn 8 có đáp án
- Trắc nghiệm Hóa học lớp 8 có đáp án
- Trắc nghiệm Địa Lí lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Tiếng Anh lớp 8 có đáp án
- Trắc nghiệm GDCD lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Lịch sử lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Vật Lí lớp 8 có đáp án
- Trắc nghiệm Công nghệ lớp 8 có đáp án
- Trắc nghiệm Tin học lớp 8 có đáp án
- Trắc nghiệm Sinh học lớp 9 có đáp án
- Trắc nghiệm Toán lớp 9 có đáp án
- Trắc nghiệm Ngữ văn 9 có đáp án
- Trắc nghiệm Hóa học lớp 9 có đáp án
- Trắc nghiệm Địa lí lớp 9 có đáp án
- Trắc nghiệm Tiếng Anh lớp 9 có đáp án
- Trắc nghiệm GDCD lớp 9 có đáp án
- Trắc nghiệm Lịch sử lớp 9 có đáp án
- Trắc nghiệm Vật lí lớp 9 có đáp án
- Trắc nghiệm Công nghệ lớp 9 có đáp án
- Trắc nghiệm Sinh học lớp 10 có đáp án
- Trắc nghiệm Toán lớp 10 có đáp án
- Trắc nghiệm Hóa học lớp 10 có đáp án
- Trắc nghiệm Ngữ văn lớp 10 có đáp án
- Trắc nghiệm Vật Lí lớp 10 có đáp án
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án
- Trắc nghiệm Sinh học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Toán lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Hóa học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn lớp 11 có đáp án
- Trắc nghiệm Tiếng Anh lớp 11 có đáp án
- Trắc nghiệm Vật Lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Địa lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm GDCD lớp 11 có đáp án
- Trắc nghiệm Lịch sử lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Công nghệ lớp 11 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 11 có đáp án
- Trắc nghiệm Tin học lớp 11 có đáp án
