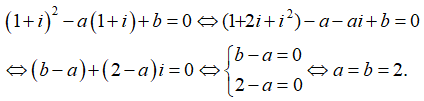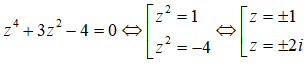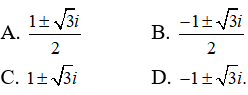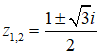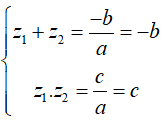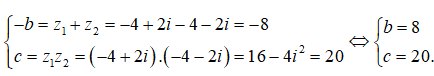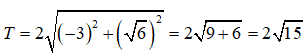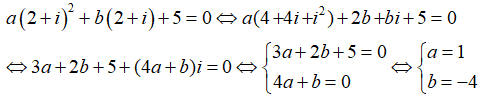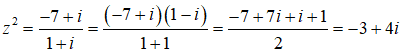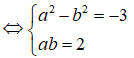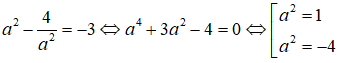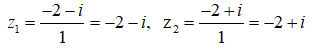TOP 40 câu Trắc nghiệm Phương trình bậc hai với hệ số thực (có đáp án 2024) - Toán 12
Bộ 40 câu hỏi trắc nghiệm Toán lớp 12 Bài 4: Phương trình bậc hai với hệ số thực có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 12 Bài 4.
Trắc nghiệm Toán 12 Bài 4: Phương trình bậc hai với hệ số thực
Bài giảng Trắc nghiệm Toán 12 Bài 4: Phương trình bậc hai với hệ số thực
Câu 1: (Đề tham khảo – Bộ GD & ĐT 2018) Gọi z1z1 và z2 là hai nghiệm phức của phương trình 4z2−4z+3=0. Giá trị của biểu thức |z1|+|z2| bằng
A. 3√2
B. 2√3
C. 3
D. √3
Đáp án: D
Giải thích:
Ta có 4z2−4z+3=0
⇔z=12±√22i
⇒|z1|+|z2|=√3
Câu 2: (Đề thi THPT Quốc gia năm 2017 – Mã đề 101) Phương trình nào dưới đây nhận hai số phức 1+√2i và 1-√2i là nghiệm?
A. z2+2z+3=0
B. z2−2z−3=0
C. z2−2z+3=0
D. z2+2z−3=0
Đáp án: C
Giải thích:
Ta có {(1+√2i)+(1−√2i)=2(1+√2i)(1−√2i)=3
⇒z2−2z+3=0.
Câu 3: (Đề thi THPT Quốc gia năm 2017 – Mã đề 102) Kí hiệu z1,z2 là hai nghiệm phức của phương trình 3z2−z+1=0 . Tính P=|z1|+|z2| .
A. P=√33
B. P=2√33
C. P=23
D. P=√143
Đáp án: B
Giải thích:
3z2−z+1=0
⇔z=16±√116i
⇒P=|z1|+|z2|=2√33.
Câu 4: (Đề thi THPT Quốc gia năm 2017 – Mã đề 103) Kí hiệu z1,z2 là hai nghiệm phức của phương trình z2−z+6=0 . Tính P=1z1+1z2 .
A. P=16
B. P=112
C. P=−16
D. P=6
Đáp án: A
Giải thích:
Ta có {z1+z2=1z1z2=6
⇒P=1z1+1z2
=z2+z2z1z2=16.
Câu 5: (Đề thi THPT Quốc gia năm 2017 – Mã đề 103) Kí hiệu z1,z2 là hai nghiệm của phương trình z2+4=0 . Gọi M,N lần lượt là điểm biểu diễn của z1,z2 trên mặt phẳng tọa độ. Tính T=OM+ON với O là gốc tọa độ.
A. √2
B. 2
C. 8
D. 4
Đáp án: D
Giải thích:
Ta có: z2+4=0
⇔z=±2i
⇒M(0;2),N(0;−2)
⇒T=OM+ON=4.
Câu 6: (Đề minh họa lần 1 – Bộ GD & ĐT năm 2017) Kí hiệu z1,z2,z3 và z4 là bốn nghiệm phức của phương trình z4−z2−12=0 . Tính T=|z1|+|z2|+|z3|+|z4|.
A. T=4
B. T=2√3
C. T=4+2√3
D. T=2+2√3
Đáp án: C
Giải thích:
Ta có:
z4−z2−12=0
⇔[z2=4z2=−3⇔[z=±2z=±√3i
⇒T=|z1|+|z2|+|z3|+|z4|
=4+2√3.
Câu 7: (Đề minh họa lần 2 – Bộ GD & ĐT năm 2017) Kí hiệu z0 là nghiệm phức có phần ảo dương của phương trình 4z2−16z+17=0 . Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức w=iz0 ?
A. M1(12;2)
B. M2(−12;2)
C. M3(−14;1)
D. M4(14;1)
Đáp án: B
Giải thích:
Ta có: 4z2−16z+17=0
⇔z=2±12i
⇒z0=2+12i
⇒w=iz0=−12+2i
⇒M(−12;2).
Câu 8: (Đề minh họa lần 3 – Bộ GD & ĐT năm 2017) Kí hiệu z1,z2 là hai nghiệm của phương trình z2+z+1=0 . Tính P=z21+z22+z1z2 .
A. 1
B. 2
C. -1
D. 0
Đáp án: D
Giải thích:
Ta có: {z1+z2=−1z1z2=1
⇒P=z21+z22+z1z2
=(z1+z2)2−z1z2=0.
Câu 9: (Sở GD & ĐT Tp. Hồ Chí Minh cụm 2 năm 2017) Gọi z1,z2 nghiệm của phương trình z2+4z+5=0 .Tìm w=(1+z1)100+(1+z2)100 .
A. w=250i
B. w=−251
C. w=251
D. w=−250i
Đáp án: B
Giải thích:
Ta có: z2+4z+5=0⇔z=−2±i
Do đó w=(1+z1)100+(1+z2)100
=(1+i)100+(1−i)100
=(2i)50+(−2i)50
=−2.250=−251.
Câu 10: (Sở GD & ĐT Tp. Hồ Chí Minh cụm 6 năm 2017) Tìm các căn bậc hai của -12 trong tập số phức ℂ .
A. ±4√3i
B. ±2√3i
C. ±2√2i
D. ±3√2i
Đáp án: B
Giải thích:
Ta có √−12=√12i2=±2√3i.
Câu 11: (Sở GD & ĐT Tp Hồ Chí Minh cụm 6 năm 2017) Cho số phức z=x+yi(x,y∈ℤ) thỏa mãn z3=18+26i. Tính T=(z−2)2+(4−z)2.
A. 2
B. 4
C. 0
D. 1
Đáp án: C
Giải thích:
Ta có: z3=18+26i⇔(3+i)3
⇔z=3+i
⇒T=(z−2)2+(4−z)2
=(1+i)2+(1−i)2=0.
Câu 12: Tìm số nguyên x, y sao cho số phức z=x+yi thỏa mãn z3=18+26i .
A. {x=3y=±1
B. {x=3y=−1
C. {x=3y=1
D. {x=−3y=±1
Đáp án: C
Giải thích:
Ta có: z3=18+26
⇔z3=(3+i)3⇔3+i
⇒x=3,y=1.
Câu 13: (Sở GD & ĐT Tp. Hồ Chí Minh cụm 7 năm 2017) Tìm tập nghiệm của phương trình z4−2z2−8=0.
A. {±2;±4i}
B. {±√2;±2i}
C. {±√2i;±2}
D. {±2;±4i}
Đáp án: C
Giải thích:
Ta có: z4−2z2−8=0
⇔[z2=−2z2=4⇔[z=±√2iz=±2
Câu 14: Gọi z1,z2 là hai nghiệm phức của phương trình z2−2z+2=0 . Tính I=z1001+z1002 .
A. M=−251
B. M=251
C. M=251i
D. M=250
Đáp án: A
Giải thích:
Ta có: z2−2z+2=0
⇔z=1±i
⇒I=z1001+z1002
=(1+i)100+(1−i)100
=−251
Câu 15: Trên trường số phức ℂ , cho phương trình az2+bz+c=0(a,b,c∈ℝ,a≠0) . Tìm khẳng định sai trong các khẳng định sau?
A. Phương trình luôn có nghiệm.
B. Tổng hai nghiệm bằng −ba
C. Tích hai nghiệm bằng ca
D. b2−4az<0 phương trình vô nghiệm
Đáp án: D
Giải thích:
Đáp án D sai.
Câu 16: Gọi M1,M2 là hai điểm lần lượt biểu diễn cho các số phức z1,z2 là nghiệm của phương trình z2+2z+4=0 . Tính số đo góc ^M1OM2 .
A. ^M1OM2=120∘
B. ^M1OM2=90∘
C. ^M1OM2=60∘
D. ^M1OM2=150∘
Đáp án: A
Giải thích:
Ta có: z2+2z+4=0
⇔z=−1±√3
⇒M1(−1;√3),M2(−1;−√3)
Ta có →OM1=(−1;√3),→OM2=(−1;−√3)
⇒cos^(→OM1,→OM2)=−12
⇒^M1OM2=120∘
Câu 17: Gọi A và B là hai điểm trong mặt phẳng biểu diễn hai nghiệm phân biệt của phương trình z2+4z+5=0. Tính tan ^AOB .
A. tan ^AOB=12
B. tan ^AOB=1
C. tan ^AOB=43
D. tan ^AOB=√3
Đáp án: C
Giải thích:
Ta có:
z2+4z+5=0
⇔z=−2±i
⇒A(−2;1),B(−2;−1)
⇒tan^AOB=43.
Câu 18: Gọi A, B là hai điểm biểu diễn hai nghiệm phức của phương trình z2+2z+10=0. Tính độ dài đoạn thẳng AB.
A. AB = 6
B. AB = 2
C. AB = 12
D. AB = 4
Đáp án: A
Giải thích:
Ta có:
z2+2z+10=0
⇔z=−1±3i
⇒A(−1;3),B(−1;−3)
⇒AB=6.
Câu 19: Gọi z1 và z2 là các nghiệm của phương trình z2−4z+9=0 . Gọi M, N là các điểm biểu diễn của z1 và z2 trên mặt phẳng phức. Khi đó độ dài của MN là:
A. MN=4
B. MN=5
C. MN=−2√5
D. MN=2√5
Đáp án: D
Giải thích:
Ta có: z2−4z+9=0
⇒z=2±√5i
⇒M(2;√5),N(2;−√5)
⇒MN=2√5.
Câu 20: Biết phương trình z2+2z+26=0 có hai nghiệm phức z1,z2 . Xét các khẳng định:
(1):z1z2=26
(2):z1 là số phức liên hợp của z2
(3):z1+z2=−2
(4):|z1|>|z2|
Hỏi có bao nhiêu khẳng định đúng?
A. 1
B. 2
C. 3
D. 4
Đáp án: C
Giải thích:
Ta có {z1+z2=−2z1z2=26.
Ta có z1=−1+5i,z2=−1−5i nên z1 là số phức liên hợp của z2
Do đó khẳng định (1), (2), (3) đúng.
Câu 21: Xét phương trình 2z4−3z2−2=0 trong tập số phức ℂ . Gọi z1,z2,z3,z4 là bốn nghiệm của phương trình. Tính tổng T=|z1|+|z2|+|z3|+|z4|.
A. T=3√2.
B. T=5√2.
C. T=5.
D. T=√2.
Đáp án: A
Giải thích:
Ta có
2z4-3z2-2=0
⇔[z2=2z2=−12⇔[z=±√2z=±1√2i
⇒T=|z1|+|z2|+|z3|+|z4|=3√2
Câu 22: Gọi z1,z2,z3,z4 là bốn nghiệm của phương trình z4−2z2−8=0. Trên mặt phẳng tọa độ, gọi A,B,C,D lần lượt là bốn điểm biểu diễn bốn nghiệm z1,z2,z3,z4 đó. Tính giá trị của biểu thức P=OA+OB+OC+OD, trong đó O là gốc tọa độ.
A. P=4.
B. P=2+√2.
C. P=2√2.
D. P=4+2√2.
Đáp án: D
Giải thích:
Ta có z4−2z2−8=0
⇔[z2=4z2=−2⇔[z=±2z=±√2i
⇒P=OA+OB+OC+OD
=4+2√2
Câu 23: Hai giá trị x1=a+bi,x2=a−b là hai nghiệm của phương trình nào sau đây?
A. x2+2ax+a2+b2=0.
B. x2+2ax+a2−b2=0.
C. x2−2ax+a2+b2=0.
D. x2−2ax+a2−b2=0.
Đáp án: C
Giải thích:
Ta có {x1+x2=2ax1x2=a2+b2
⇒x2−2ax+a2+b2=0.
Câu 24: Tính tổng phần thực, phẩn ảo của số phức 1z thỏa mãn z2−2(1+i)z+2i=0.)
A. 1
B. 0
C. -1
D. -2.
Đáp án: B
Giải thích:
z2−2(1+i)z+2i=0
⇔z2−2(1+i)z+(1+i)2=0
⇔(z−1−i)2=0
⇔z=1+i
Ta có 11+i=1−i(1+i)(1−i)
=1−i2=12−12i
⇒ tổng phần thực và phần ảo bằng 0.
Câu 25: Gọi z1,z2 là hai nghiệm phức của phương trình z2−3z+3=0. Tính P=1|z1|2+1|z2|2
A. P=23
B. P=13
C. P=49
D. P=29
Đáp án: A
Giải thích:
z2−3z+3=0
⇔z=32±√32i
⇒P=1|z1|2+1|z2|2
=23.
Câu 26: Gọi z1,z2 là hai nghiệm phức của phương trình z2−4z+5=0 . Tính P=|z1|2+|z2|2.
A. M=2√34
B. M=4√5
C. M=12
D. M=10
Đáp án: D
Giải thích:
Ta có: z2+2z+5=0
⇔z=−1±2i
⇒M=|z1|2+|z2|2=10.
Câu 27: Gọi z1,z2 là hai nghiệm của phương trình z+1z=−1. Tính P=z31+z32.
A. 0
B. 1
C. 2
D. 3
Đáp án: C
Giải thích:
z2+z+1=0
⇒{z1+z2=−1z1z2=1
⇒P=(z1+z2)3−3z1z2(z1+z2)
= 2
Câu 28: Gọi z1,z2 là hai nghiệm của phương trình √3z2−z+6=0 . Tính A=z31+z32.
A. A=−5,8075
B. A=54−√39
C. A=√3+54−9
D. A=√3−549.
Đáp án: D
Giải thích:
Ta có {z1+z2=1√3z1z2=2√3
⇒A=(z1+z2)3−3z1z2(z1+z2)
=−54+√39.
Câu 29: Gọi x0 là nghiệm phức có phần ảo là số dương của phương trình x2+x+2=0 . Tìm số phức z=x20+2x0+3.
A. z=1+√7i.
B. z=−2√7i.
C. z=1+√7i2.
D. z=√7i−32.
Đáp án: C
Giải thích:
(x+12)2=−74=74i2
⇔x=−12±√72i
⇒x0=12±i√72
⇒z=1+i√72
Câu 30: Gọi z1 là nghiệm phức có phần ảo âm của phương trình z2+4z+20=0. Tính giá trị của biểu thức A=|z1|2+(z21+z22).
A. 0
B. 2
C. -28
D. -16
Đáp án: C
Giải thích:
(z+2)2=−16=16i2
⇔z=−2±4i
⇒z1=−2−4i;z2=−2+4i
⇒A=−28.
Câu 31: Phương trình z2 -az + b = 0 (a, b ∈ R) có nghiệm z = 1 + i khi
A. a = 2, b = -2
B. a = 2, b = 2
C. a = -2, b = 2
D. a = -2, b = -2
Đáp án: B
Giải thích:
Thay z = 1 + i vào phương trình đã cho ta có:
Câu 32: Phương trình z4 + 3z2 - 4 = 0 có 4 nghiệm phức z1, z2, z3, z4. Giá trị biểu thức T = |z1| + |z2| + |z3| + |z4| bằng
A. 6
B. 2√2
C. 2 + 2√2
D. 4 + 2√2
Đáp án: A
Giải thích:
Ta có:
⇒ |z1| = |z2| = 1; |z3| = |z4| = 2
Vậy T = 1 + 1 + 2 + 2 = 6
Câu 33: Phương trình z2 - z + 1 = 0 có hai nghiệm là
Đáp án: A
Giải thích:
Ta có: Δ = 12 - 4 = -3 = 3i2
Các nghiệm của phương trình đã cho là
Câu 34: Để phương trình z2 + bz + c = 0 nhận z1 = -4 + 2i và z2 = -4 - 2i làm nghiệm thì
A. b = -8, c = 20
B. b = -8, c = -20
C. b = 8, c = 20
D. b = 8, c = 20
Đáp án: D
Giải thích:
Gọi z1, z2 là hai nghiệm của phương trình đã cho, áp dụng hệ thức Vi-ét ta có:
Để phương trình đã cho nhận z1, z2 làm nghiệm thì
Câu 35: Phương trình z2 + 6z + 15 = 0 có các nghiệm là z1, z2.Giá trị biểu thức T = |z1| + |z2| bằng:
A. 2√15
B. 6
C. 4√5
D. 2√3
Đáp án: A
Giải thích:
Ta có:Δ' = 9 - 15 = -6 = 6i2
Các nghiệm của phương trình là z1 = - 3 - i√6, z2 = - 3 + i√6
Do đó
Câu 36: Phương trình z1 = 1 + 2i, z2 = 2 - 3i có nghiệm là z = 2 + i khi
A. a = 1, b = 4
B. a = -1, b = 4
C. a = -1, b = -4
D. a = 1, b = -4
Đáp án: D
Giải thích:
Thay z = 2 + i vào phương trình đã cho ta có:
Câu 37: Phương trình (1 + i)2 = -7 + i có các nghiệm là
A. -1 - 2i và 1 + 2i
B. -1 + 2i và 1 + 2i
C. -1 + 2i và 1 - 2i
D. 1 + 2i và 1 - 2i
Đáp án: A
Giải thích:
Phương trình đã cho tương đương với
Viết -3 + 4i = 4i2 + 4i + 1 = (2i + 1)2, ta có: z2 = (2i + 1)2 <=> z = ±(2i + 1)
Chú ý: Nếu việc viết -3 + 4i = (2i + 1)2 gặp khó khăn thì có thể đặt z = a + bi (a, b ∈ R). Ta có :
(a + bi)2 = -3 + 4i <=> a2 - b2 + 2abi = -3 + 4i
Từ phương trình thứ hai của hệ ta có b = 2/a
Thay vào phương trình thứ nhất của hệ ta có
Vì a ∈ R và a2 ≥ 0 nên a2 = 1 hay a = ±1 . Từ đó ta có hai nghiệm : z1 = -1 - 2i và z2 = 1 + 2i
Câu 38: Phương trình z2 + 4x + 5 = 0 có các nghiệm là
A. 2 ± i
B. -2 ± i
C. 4 ± i
D. -4 ± i
Đáp án: B
Giải thích:
Ta có: Δ' = 22 - 1.5 = -1 = i2. Phương trình có hai nghiệm là:
Câu 39: Phương trình z2 + 8z + 17 = 0 có hai nghiệm
A. 1 - i và 1 - 2i
B. 4 - i và 4 + i
C. -4 - i và -4 + i
D. -2 + 2i và -2 + 4i
Đáp án: C
Giải thích:
Ta có: Δ = 16 - 17 = -1 = i2. Phương trình có các nghiệm là:
z1 = -4 - i, z2 = -4 + i
Câu 40: Phương trình z2 - 4z + 9 = 0 có hai nghiệm. Giá trị biểu thức T = |z1| + |z2| bằng
A. – 6
B. 6
C. 8
D. 2√3
Đáp án: B
Giải thích:
Ta có: Δ' = 4 - 9 = -5 = 5i2. Phương trình có hai nghiệm là:
z1,2 = 2 ± i√5
Vậy T = 2√(4 + 5) = 2√9 = 6
Các câu hỏi trắc nghiệm Toán lớp 12 có đáp án, chọn lọc khác:
Trắc nghiệm Ôn tập Chương 3 - Nguyên hàm - Tích phân và ứng dụng có đáp án
Trắc nghiệm Cộng, trừ và nhân số phức có đáp án
Xem thêm các chương trình khác:
- Trắc nghiệm Sinh học lớp 7 có đáp án
- Trắc nghiệm Toán lớp 7 có đáp án
- Trắc nghiệm Ngữ văn lớp 7 có đáp án
- Trắc nghiệm Sinh học 8 có đáp án
- Trắc nghiệm Toán lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn 8 có đáp án
- Trắc nghiệm Hóa học lớp 8 có đáp án
- Trắc nghiệm Địa Lí lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Tiếng Anh lớp 8 có đáp án
- Trắc nghiệm GDCD lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Lịch sử lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Vật Lí lớp 8 có đáp án
- Trắc nghiệm Công nghệ lớp 8 có đáp án
- Trắc nghiệm Tin học lớp 8 có đáp án
- Trắc nghiệm Sinh học lớp 9 có đáp án
- Trắc nghiệm Toán lớp 9 có đáp án
- Trắc nghiệm Ngữ văn 9 có đáp án
- Trắc nghiệm Hóa học lớp 9 có đáp án
- Trắc nghiệm Địa lí lớp 9 có đáp án
- Trắc nghiệm Tiếng Anh lớp 9 có đáp án
- Trắc nghiệm GDCD lớp 9 có đáp án
- Trắc nghiệm Lịch sử lớp 9 có đáp án
- Trắc nghiệm Vật lí lớp 9 có đáp án
- Trắc nghiệm Công nghệ lớp 9 có đáp án
- Trắc nghiệm Sinh học lớp 10 có đáp án
- Trắc nghiệm Toán lớp 10 có đáp án
- Trắc nghiệm Hóa học lớp 10 có đáp án
- Trắc nghiệm Ngữ văn lớp 10 có đáp án
- Trắc nghiệm Vật Lí lớp 10 có đáp án
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án
- Trắc nghiệm Sinh học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Toán lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Hóa học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn lớp 11 có đáp án
- Trắc nghiệm Tiếng Anh lớp 11 có đáp án
- Trắc nghiệm Vật Lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Địa lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm GDCD lớp 11 có đáp án
- Trắc nghiệm Lịch sử lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Công nghệ lớp 11 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 11 có đáp án
- Trắc nghiệm Tin học lớp 11 có đáp án