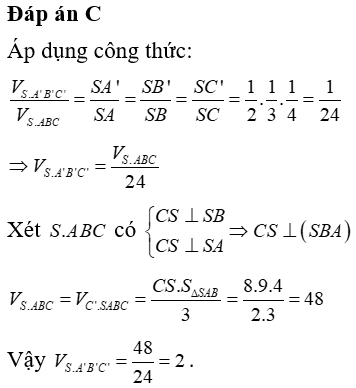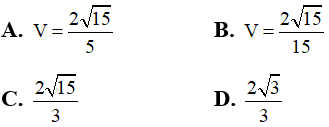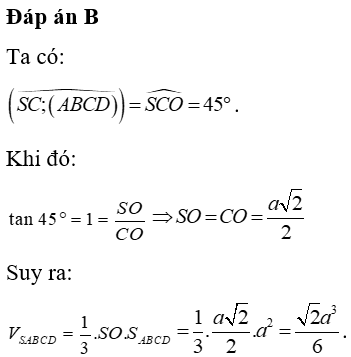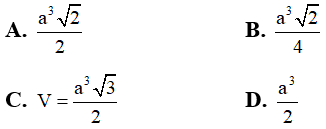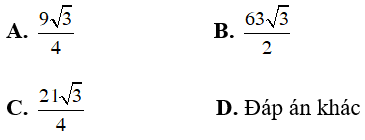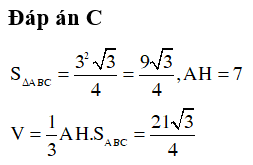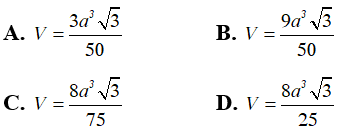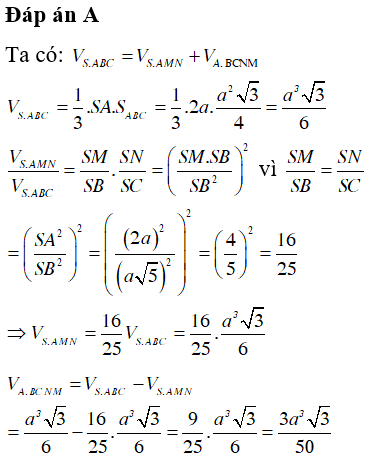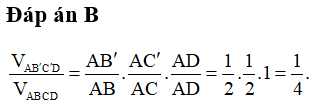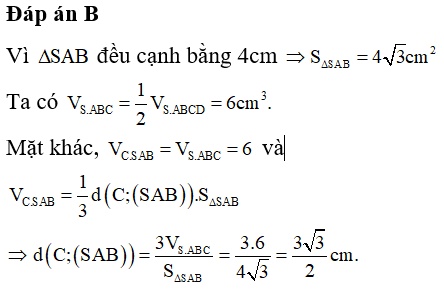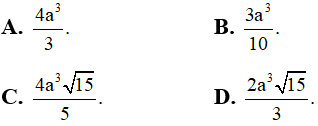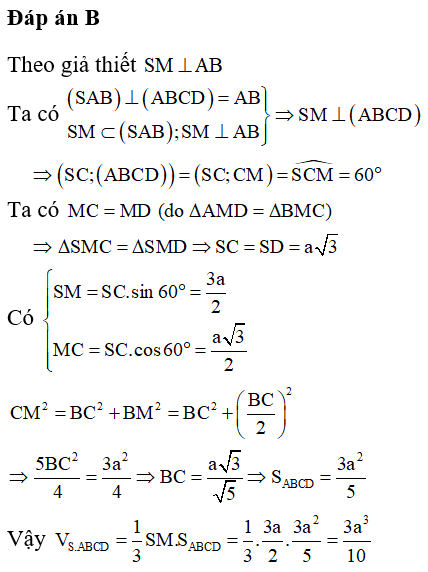TOP 40 câu Trắc nghiệm Ôn tập Chương 1 - Khối đa diện (có đáp án 2024) - Toán 12

Bộ 40 câu hỏi trắc nghiệm Toán lớp 12 Bài: Ôn tập Chương 1 - Khối đa diện có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 12 Bài Ôn tập chương 1.

1 1,476 22/12/2023

Tải về

Trang trước

Trang sau

Trắc nghiệm Toán 12 Bài Ôn tập Chương 1 - Khối đa diện

Câu 1. Khối lăng trụ đáy là hình chữ nhật có hai kích thước lần lượt là 2a, 3a, chiều cao khối lăng trụ là 5a. Tính thể tích khối lăng trụ:

A. $30 a^{3}$

B. $10 a^{3}$

C. $30 a^{2}$

D. $10 a^{2}$

Hiển thị đáp án

Đáp án: A

Giải thích:

Diện tích đáy của khối lăng trụ đã cho là:

$S = 2 a .3 a = 6 a^{2}$

$\Rightarrow$ Thể tích khối lăng trụ đã cho là:

$V = S h = 6 a^{2} .5 a = 30 a^{3}$

Câu 2. Cho khối lăng trụ ABC.A’B’C’, khoảng cách từ C đến đường thẳng BB’ bằng $\sqrt{5}$ , khoảng cách từ A đến các đường thẳng BB’ và CC’ lần lượt bằng 1 và 2, hình chiếu vuông góc của A lên mặt phẳng $(A' B' C')$ là trung điểm M của B’C’ và $A' M = \sqrt{5}$ . Thể tích của khối lăng trụ đã cho bằng:

A. $\frac{2 \sqrt{5}}{3}$

B. $\frac{2 \sqrt{15}}{3}$

C. $\sqrt{5}$

D. $\frac{\sqrt{15}}{3}$

Hiển thị đáp án

Đáp án: B

Giải thích:

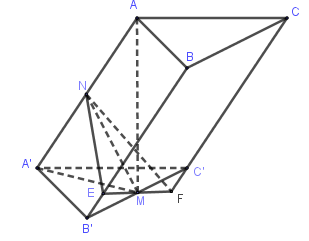
Qua M dựng mặt phẳng (P) vuông góc với AA’ cắt các cạnh AA’, BB’, CC’ lần lượt tại N, E, F.

Ta có:

$A A' ⊥ N E \Rightarrow N E = d (E, A A')$

$= d (N, B B') = d (A, B B') = 1$

$A A' ⊥ N F \Rightarrow N F = d (F, A A')$

$= d (N, C C') = d (A, C C') = 2$

$A A' ⊥ (P) \Rightarrow C C' ⊥ (P) \Rightarrow E F ⊥ C C'$

$\Rightarrow E F = d (E, C C') = d (F, B B')$

$= d (C, B B') = \sqrt{5}$

Có: $N E^{2} + N F^{2} = E F^{2} \Rightarrow Δ N E F$

vuông tại N (định lí Pitago)

$\Rightarrow M N = \frac{1}{2} E F = \frac{\sqrt{5}}{2}$

Xét tam giác AA’M vuông tại M, ta có:

$\frac{1}{M N^{2}} = \frac{1}{A M^{2}} + \frac{1}{A' M^{2}}$

$\Leftrightarrow \frac{4}{5} = \frac{1}{A M^{2}} + \frac{1}{5}$

$\Leftrightarrow A M = \frac{\sqrt{15}}{3}$

Ta có: $\{\begin{matrix} (P) ⊥ A A' \\ (A' B' C') ⊥ A M \end{matrix}$

$\Rightarrow (\hat{(P), (A' B' C')}) = (\hat{A A', A M}) = \hat{A' M A}$

$\Rightarrow \cos \hat{A' M A} = \frac{A M}{A A'}$

$= \frac{\frac{\sqrt{15}}{3}}{\sqrt{5 + \frac{5}{3}}} = \frac{1}{2}$

Ta thấy $Δ N E F$ là hình chiếu vuông góc của $Δ A' B' C'$ lên mặt phẳng (P)

$\Rightarrow S_{A' B' C'} = \frac{S_{N E F}}{\cos \hat{A' A M}}$

$= \frac{\frac{1}{2} N E . N F}{\frac{1}{2}}$

$= 1.2 = 2$

$\Rightarrow V_{A B C . A' B' C'} = S_{A' B' C'} . A M$

$= 2. \frac{\sqrt{15}}{3} = \frac{2 \sqrt{15}}{3}$

Câu 3. Cho tứ diện đều ABCD có cạnh bằng 3. Gọi M, N là hai điểm thay đổi lần lượt thuộc cạnh BC, BD sao cho mặt phẳng (AMN) luôn vuông góc với mặt phẳng (BCD). Gọi $V_{1}, V_{2}$ lần lượt là giá trị lớn nhất và nhỏ nhất của thể tích khối tứ diện ABMN. Tính $V_{1} + V_{2}$ ?

A. $\frac{17 \sqrt{2}}{8}$

B. $\frac{51 \sqrt{2}}{16}$

C. $\frac{\sqrt{2}}{4}$

D. $\frac{51 \sqrt{2}}{8}$

Hiển thị đáp án

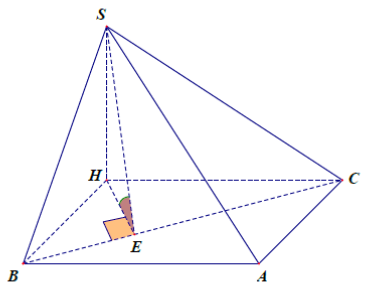
Đáp án: A

Giải thích:

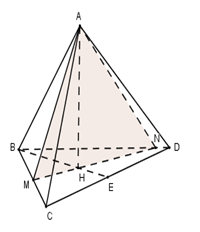
Tứ diện ABCD đều, gọi H là tâm tam giác đều

$B C D \Rightarrow A H ⊥ (B C D)$

Có $(A M N) ⊥ (B C D)$

$\Rightarrow (A M N) \supset A H \Rightarrow H \in M N$

$\Rightarrow V_{A B M N} = \frac{1}{3} A H . S_{B M N}$ với AH không đổi.

Dễ thấy diện tích tam giác BMN nhỏ nhất khi và chỉ khi tam giác BMN đều, khi đó $M N / / C D$

$\frac{B M}{B C} = \frac{B H}{B E} = \frac{2}{3}$

$\Rightarrow B M = \frac{2}{3} B C = 2$

$\Rightarrow S_{B M N_{\min}} = \frac{2^{2} \sqrt{3}}{4} = \sqrt{3}$

Diện tích BMN lớn nhất khi và chỉ khi $[\begin{matrix} N \equiv D \\ M \equiv C \end{matrix}$ , khi đó:

$S_{B M N_{\max}} = \frac{1}{2} B E = \frac{2}{3} . \frac{3 \sqrt{3}}{2} = \sqrt{3}$

$\Rightarrow A H = \sqrt{A B^{2} - B H^{2}}$

$= \sqrt{3^{2} - {(\sqrt{3})}^{2}} = \sqrt{6}$

$\Rightarrow V_{1} = \frac{1}{3} . A H . S_{B M N_{\max}}$

$= \frac{1}{3} \sqrt{6} . \frac{9 \sqrt{3}}{8} = \frac{9 \sqrt{2}}{8}$

$\Rightarrow V_{2} = \frac{1}{3} . A H . S_{B M N_{\min}}$

$= \frac{1}{3} \sqrt{6} . \sqrt{3} = \sqrt{2}$

$\Rightarrow V_{1} + V_{2} = \frac{17 \sqrt{2}}{8}$

Câu 4. Thể tích của khối hộp chữ nhật có ba kích thước lần lượt là 1, 2, 3 bằng:

A. 2

B. 3

C. 1

D. 6

Hiển thị đáp án

Đáp án: D

Giải thích:

Hình hộp chữ nhật có 3 kích thước lần lượt 1, 2, 3 là: V = 1.2.3 = 6

Câu 5. Khối chóp tam giác có độ dài 3 cạnh xuất phát từ một đỉnh là a, 2a, 3a có thể tích lớn nhất bằng:

A. $4 a^{3}$

B. $2 a^{3}$

C. $a^{3}$

D. $6 a^{3}$

Hiển thị đáp án

Đáp án: C

Giải thích:

Xét khối chóp tam giác S.ABC,

có $\{\begin{matrix} S A = a, S B = 2 a \\ S C = 3 a, \hat{A S B} = α \end{matrix}$

và h là khoảng cách từ C đến (SAB)

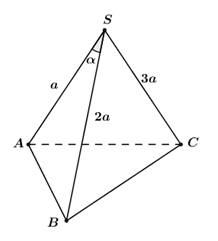
Trắc nghiệm Ôn tập Chương I - Khối đa diện có đáp án - Toán lớp 12 (ảnh 4)

Khi đó, thể tích khối chóp S.ABC là

$V = \frac{1}{3} . d (C; (S A B)) . S_{Δ S A B}$ (1)

Diện tích tam giác SAB là

$S_{Δ S A B} = \frac{1}{2} . S A . S B . \sin \hat{A S B} = a^{2} . \sin α$ (2)

Từ (1) và (2) suy ra:

$V = \frac{1}{3} . h . a^{2} . \sin α$

mà $\{\begin{matrix} \sin α \leq 1 \\ h \leq S C = 3 a \end{matrix}$

$\Rightarrow V \leq \frac{1}{3} .3 a . a^{2} = a^{3}$

Dầu “=” xảy ra khi

$\sin α = 1, h = S C = 3 a$

hay hình chóp S.ABC là tứ diện vuông đỉnh S.

Câu 6. Khối hộp chữ nhật có các kích thước lần lượt là a, 2a, 3a có thể tích bằng:

A. $\frac{3 a^{3} \sqrt{2}}{5}$

B. $6 a^{3}$

C. $2 a^{3}$

D. $6 a^{2}$

Hiển thị đáp án

Đáp án: B

Giải thích:

Thể tích khối hộp chữ nhật là

$V = a .2 a .3 a = 6 a^{3}$

Câu 7. Cho khối lăng trụ tam giác $A B C . A' B' C'$ có thể tích V. Trên đáy A’B’C’ lấy điểm M bất kì. Thể tích khối chóp M.ABC tính theo V bằng:

A. $\frac{V}{2}$

B. $\frac{2 V}{3}$

C. $\frac{V}{3}$

D. $\frac{3 V}{4}$

Hiển thị đáp án

Đáp án: C

Giải thích:

Vì $M \in (A' B' C')$

$\Rightarrow d (M; (A B C)) = d ((A' B' C'); (A B C))$

$\Rightarrow V_{M . A B C} = \frac{1}{3} d (M, (A B C)) . S_{A B C} = \frac{1}{3} V$

Câu 8. Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a và $\hat{B A D} = 60 °$ , AB’ hợp với đáy (ABCD) một góc $30 °$ . Thể tích của khối hộp là:

A. $\frac{a^{3}}{2}$

B. $\frac{a^{3}}{6}$

C. $\frac{a^{3} \sqrt{2}}{6}$

D. $\frac{3 a^{3}}{2}$

Hiển thị đáp án

Đáp án: A

Giải thích:

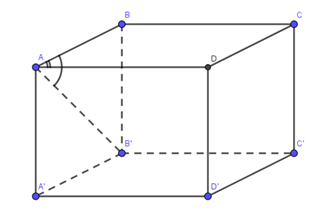
ABCD.’B’C’D’ là hình hộp đứng

$\Rightarrow B B' ⊥ (A B C D)$

$\Rightarrow (\hat{A B'; (A B C D)}) = (\hat{A B'; A B})$

$= \hat{B A B'} = 30 °$

Tam giác ABB’ vuông tại B

$\Rightarrow \tan \hat{B A B'} = \frac{B B'}{A B}$

$\Rightarrow B B' = A B . \tan 30 ° = \frac{a}{\sqrt{3}}$

Tam giác ABD có:

$A B = A D = a, \hat{B A D} = 60 °$

$\Rightarrow$ tam giác ABD đều, có cạnh đều bằng a.

$\Rightarrow S_{A B D} = \frac{a^{2} \sqrt{3}}{4}$

$\Rightarrow S_{A B C D} = 2. S_{A B D}$

$= 2. \frac{a^{2} \sqrt{3}}{4} = \frac{a^{2} \sqrt{3}}{2}$

Thể tích khối hộp ABCD.A’B’C’D’:

$V = S_{A B C D} . B B' = \frac{a^{2} \sqrt{3}}{2} . \frac{a}{\sqrt{3}}$

$= \frac{a^{3}}{2}$

Câu 9. Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại A. $A B = a; A C = a \sqrt{3}; A A' = 2 a$ . Thể tích khối lăng trụ ABC.A’B’C’ là:

A. $a^{3} \sqrt{3}$

B. $\frac{a^{3} \sqrt{3}}{3}$

C. $2 a^{3} \sqrt{3}$

D. $\frac{2 a^{3} \sqrt{3}}{3}$

Hiển thị đáp án

Đáp án: A

Giải thích:

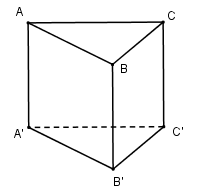
Trắc nghiệm Ôn tập Chương I - Khối đa diện có đáp án - Toán lớp 12 (ảnh 7) $S_{A B C} = \frac{1}{2} A B . A C = \frac{1}{2} a . a \sqrt{3}$

$= \frac{a^{2} \sqrt{3}}{2}$

$\Rightarrow V_{A B C . A' B' C'} = A A' . S_{A B C}$

$= 2 a . \frac{a^{2} \sqrt{3}}{2} = a^{3} \sqrt{3}$

Câu 10. Cho khối lập phương có thể tích bằng 27, diện tích toàn phần của khối lập phương đã cho bằng:

A. 75

B. 36

C. 18

D. 54

Hiển thị đáp án

Đáp án: D

Giải thích:

Cạnh của khối lập phương đã cho là: $a = \sqrt[3]{27} = 3$ diện tích toàn phần của khối lập phương đã cho là: ${6.3}^{2} = 54$

Câu 11. Cho khối chóp tứ giác đều có cạnh đáy bằng a, chiều cao bằng $\frac{a \sqrt{2}}{2}$ . Thể tích khối chóp đã cho bằng:

A. $\frac{a^{3} \sqrt{3}}{4}$

B. $\frac{a^{3} \sqrt{2}}{3}$

C. $\frac{a^{3} \sqrt{2}}{2}$

D. $\frac{a^{3} \sqrt{2}}{6}$

Hiển thị đáp án

Đáp án: D

Giải thích:

Thể tích của khối chóp đã cho là:

$V = \frac{1}{3} S h = \frac{1}{3} . a^{2} . \frac{a \sqrt{2}}{2} = \frac{a^{3} \sqrt{2}}{6}$

Câu 12. Cho hình chóp S.ABC có đáy ABC vuông tại A và SB vuông góc với đáy. Biết SB = a, SC hợp với (SAB) một góc $30 °$ và (SAC) hợp với đáy (ABC) một góc $60 °$ . Thể tích của khối chóp là:

A. $\frac{a^{3} \sqrt{3}}{27}$

B. $\frac{a^{3} \sqrt{3}}{9}$

C. $\frac{a^{3}}{27}$

D. $\frac{a^{3}}{9}$

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có:

$\begin{matrix} A C ⊥ A B \\ A C ⊥ S B (S B ⊥ (A B C)) \end{matrix}\}$

$\Rightarrow A C ⊥ (S A B) \Rightarrow A C ⊥ S A$

$\Rightarrow$ SA là hình chiếu vuông góc của SC trên (SAB)

$\Rightarrow (\hat{S C; (S A B)}) = (\hat{S C; S A})$

$= \hat{C S A} = 30 °$

$\begin{matrix} (S A C) \cap (A B C) = A C \\ (S A C) \supset S A ⊥ A C \\ (A B C) \supset A B ⊥ A C \end{matrix}\}$

$\Rightarrow (\hat{(S A C); (A B C)}) = (\hat{S A; A B})$

$= \hat{S A B} = 60 °$

$S B ⊥ (A B C) \Rightarrow S B ⊥ A B$

$\Rightarrow Δ S A B$ vuông tại B

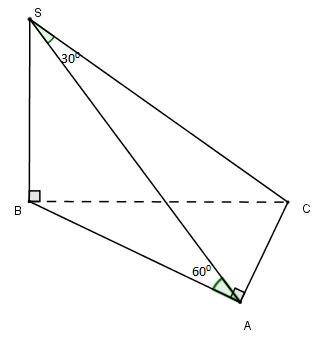
Trắc nghiệm Ôn tập Chương I - Khối đa diện có đáp án - Toán lớp 12 (ảnh 8) $\Rightarrow A B = S B . \cos 60 ° = a . \frac{1}{\sqrt{3}} = \frac{a \sqrt{3}}{3}$

$\Rightarrow S A = \sqrt{S B^{2} + A B^{2}}$

$= \sqrt{a^{2} + \frac{a^{3}}{3}} = \frac{2 a}{\sqrt{3}}$

Xét tam giác vuông SAC ta có:

$A C = S A . \tan 30 ° = \frac{2 a}{\sqrt{3}} . \frac{1}{\sqrt{3}} = \frac{2 a}{3}$

$S_{A B C} = \frac{1}{2} A B . A C$

$= \frac{1}{2} . \frac{a \sqrt{3}}{3} . \frac{2 a}{3} = \frac{a^{2} \sqrt{3}}{9}$

$V_{S . A B C} = \frac{1}{3} S B . S_{A B C}$

$= \frac{1}{3} . a . \frac{a^{2} \sqrt{3}}{9} = \frac{a^{3} \sqrt{3}}{27}$

Câu 13. Cho tứ diện ABCD có $A D = 14, B C = 6$ . Gọi M, N lần lượt là trung điểm của các cạnh AC, BD và MN = 8. Gọi là góc giữa hai đường thẳng BC và MN. Tính

A. $\frac{2 \sqrt{2}}{3}$

B. $\frac{\sqrt{3}}{2}$

C. $\frac{1}{2}$

D. $\frac{\sqrt{2}}{4}$

Hiển thị đáp án

Đáp án: B

Giải thích:

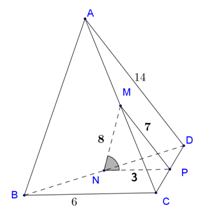
Trắc nghiệm Ôn tập Chương I - Khối đa diện có đáp án - Toán lớp 12 (ảnh 9)

Gọi P là trung điểm của cạnh CD, ta có

$α = (\hat{M N; B C}) = (\hat{M N; N P})$

Trong tam giác MNP, ta có:

$\cos \hat{M N P} = \frac{M N^{2} + P N^{2} - M P^{2}}{2 M N . N P}$

$= \frac{1}{2} \Rightarrow \hat{M N P} = 60 °$

Suy ra $\sin α = \frac{\sqrt{3}}{2}$

Câu 14. Một lăng trụ đứng tam giác có các cạnh đáy là 11cm, 12cm, 13cm và diện tích xung quanh bằng $144 c m^{2}$ . Thể tích của khối lăng trụ đó là:

A. $24 \sqrt{105} c m^{3}$

B. $12 \sqrt{105} c m^{3}$

C. $18 \sqrt{105} c m^{3}$

D. $6 \sqrt{105} c m^{3}$

Hiển thị đáp án

Đáp án: A

Giải thích:

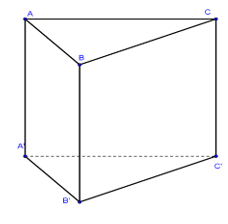
Ta có: $S_{x q} = (11 + 12 + 13) h = 144$

$\Rightarrow h = \frac{144}{36} = 4$

Nửa chu vi đáy là:

$\frac{11 + 12 + 13}{2} = 18$

Diện tích đáy:

$S_{d} = \sqrt{18 (18 - 11) (18 - 12) (18 - 13)}$

$= 6 \sqrt{105}$

Vậy thể tích khối lăng trụ:

$V = S_{d} . h =$ $24 \sqrt{105} c m^{3}$

Câu 15. Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a, $S A ⊥ (A B C)$ và $S A = a$ . Tính thể tích khối chóp S.ABC

A. $V_{S . A B C} = \frac{a^{3} \sqrt{3}}{6}$

B. $V_{S . A B C} = \frac{a^{3} \sqrt{3}}{4}$

C. $V_{S . A B C} = \frac{a^{3} \sqrt{3}}{12}$

D. $V_{S . A B C} = \frac{a^{3} \sqrt{3}}{3}$

Hiển thị đáp án

Đáp án: C

Giải thích:

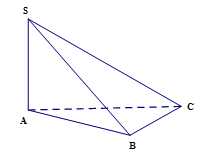
Ta có: $S A = a, S_{Δ A B C} = \frac{a^{2} \sqrt{3}}{4}$ .

Suy ra thể tích $V_{S . A B C} = \frac{1}{3} S A . S_{Δ A B C}$

$\Rightarrow V_{S . A B C} = \frac{a^{3} \sqrt{3}}{12}$

Câu 16. Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a, $S A ⊥ (A B C D)$ và $S A = a \sqrt{6}$ . Thể tích của khối chóp S.ABCD bằng:

A. $\frac{a^{3} \sqrt{6}}{6}$

B. $a^{3} \sqrt{6}$

C. $\frac{a^{3} \sqrt{6}}{3}$

D. $\frac{a^{3} \sqrt{6}}{2}$

Hiển thị đáp án

Đáp án: C

Giải thích:

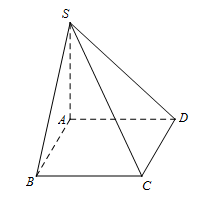
Trắc nghiệm Ôn tập Chương I - Khối đa diện có đáp án - Toán lớp 12 (ảnh 12) $V_{S . A B C D} = \frac{1}{3} S A . S_{A B C D}$

$= \frac{1}{3} . a \sqrt{6} . a^{2} = \frac{a^{3} \sqrt{6}}{3}$

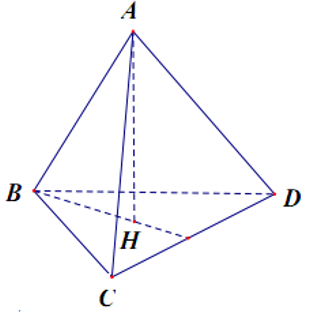
Câu 17. Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau, $A B = 6 a, A C = 7 a, A D = 4 a$ . Gọi M, N, P lần lượt là trung điểm của các cạnh BC, CD, DB. Thể tích V của tứ diện AMNP là:

A. $V = \frac{7 a^{3}}{2}$

B. $V = 14 a^{3}$

C. $V = \frac{28 a^{3}}{3}$

D. $V = 7 a^{3}$

Hiển thị đáp án

Đáp án: D

Giải thích:

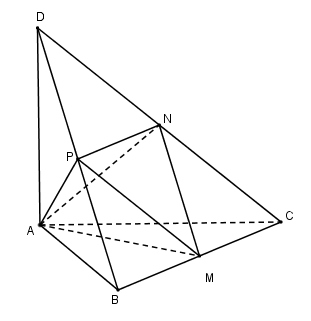
Ta có:

ABCD là tứ diện vuông tại A nên

$V_{A B C D} = \frac{1}{6} A B . A C . A D$

$= \frac{1}{6} .6 a .7 a .4 a = 28 a^{3}$

Áp dụng công thức tính tỉ lệ thể tích các khối tứ diện, ta có:

$\frac{V_{D A P N}}{V_{D A B C}} = \frac{D A}{D A} . \frac{D P}{D B} . \frac{D N}{D C}$

$= \frac{1}{1} . \frac{1}{2} . \frac{1}{2} = \frac{1}{4}$

$\Rightarrow V_{D A P N} = \frac{1}{4} V_{D A B C}$

$= \frac{1}{4} .28 a^{3} = 7 a^{3}$

$\frac{V_{B A P M}}{V_{B A D C}} = \frac{B A}{B A} . \frac{B P}{B D} . \frac{B M}{B C}$

$= \frac{1}{1} . \frac{1}{2} . \frac{1}{2} = \frac{1}{4}$

$\Rightarrow V_{B A P M} = \frac{1}{4} V_{B A D C}$

$= \frac{1}{4} .28 a^{3} = 7 a^{3}$

$\frac{V_{C A M N}}{V_{C A B D}} = \frac{C A}{C A} . \frac{C M}{C B} . \frac{C N}{C D}$

$= \frac{1}{1} . \frac{1}{2} . \frac{1}{2} = \frac{1}{4}$

$\Rightarrow V_{C A M N} = \frac{1}{4} V_{C A B D}$

$= \frac{1}{4} .28 a^{3} = 7 a^{3}$

Do đó:

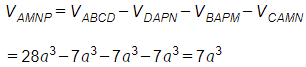
Trắc nghiệm Ôn tập Chương I - Khối đa diện có đáp án - Toán lớp 12 (ảnh 1)

Câu 18. Một hình chóp tứ giác đều có mấy mặt đối xứng:

A. 3

B. 2

C. 1

D. 4

Hiển thị đáp án

Đáp án: D

Giải thích:

Hình chóp tứ giác đều S.ABCD có đáy là hình vuông, hình chiếu của đỉnh S trên đáy trùng với tâm đáy.

Hình chóp S.ABCD có các mặt đối xứng là $(S A C), (S B D), (S G I), (S H J)$ với G, H, I, J lần lượt là trung điểm AB, BC, CD, DA.

Câu 19. Hình đa diện nào dưới đây không có tâm đối xứng?

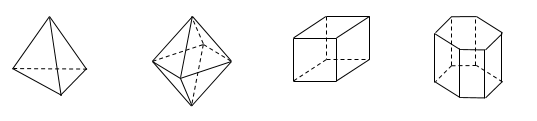
Trắc nghiệm Ôn tập Chương I - Khối đa diện có đáp án - Toán lớp 12 (ảnh 14)

A. Tứ diện đều

B. Bát diện đều

C. Hình lập phương

D. Lăng trụ lục giác đều

Hiển thị đáp án

Đáp án: A

Giải thích:

Dễ dàng thấy bát diện đều, hình lập hương và lăng trụ lục giác đều có tâm đối xứng. Còn tứ diện đều không có.

Câu 20. Cho một cây nến hình lăng trụ lục giác đều có chiều cao và độ dài cạnh đáy lần lượt là 15cm và 5cm. Người ta xếp cây nến trên vào trong một hộp có dạng hình chữ nhật sao cho cây nến nằm khít trong hộp (có đáy tiếp xức như hình vẽ). Thể tích của chiếc hộp đó bằng

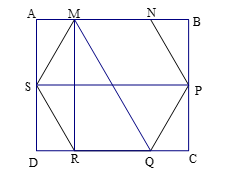
Trắc nghiệm Ôn tập Chương I - Khối đa diện có đáp án - Toán lớp 12 (ảnh 15)

A. $1500 c m^{3}$

B. $600 \sqrt{6} c m^{3}$

C. $1800 c m^{3}$

D. $750 \sqrt{3} c m^{3}$

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có: $A B = S P = 2 M N = 10 c m$

$A D = M R = \sqrt{5^{2} - {(\frac{5}{2})}^{2}} = 5 \sqrt{3}$

$\Rightarrow S_{A B C D} = A B . A D = 50 \sqrt{3} c m^{2}$

$V = S_{A B C D} . h = 50 \sqrt{3} .15 = 750 \sqrt{3} c m^{3}$

Câu 21. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cạnh C, $A B = a \sqrt{5}, A C = a$ . Cạnh bên $S A = 3 a$ và vuông góc với mặt phẳng đáy. Thể tích của khối chóp S.ABC bằng:

A. $\frac{\sqrt{5}}{2} a^{3}$

B. $3 a^{3}$

C. $a^{3}$

D. $2 a^{3}$

Hiển thị đáp án

Đáp án: C

Giải thích:

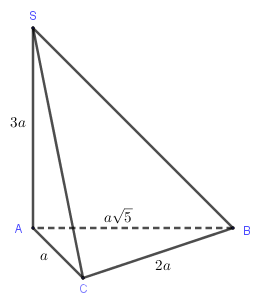
Vì tam giác ABC vuông nên áp dụng Pitago

$C B = \sqrt{A B^{2} - A C^{2}} = \sqrt{5 a^{2} - a^{2}} = 2 a$

Diện tích đáy:

$S_{Δ A B C} = \frac{1}{2} . a .2 a = a^{2}$

Thể tích khối chóp:

$V_{S . A B C} = \frac{1}{3} . S_{Δ A B C} . S A$

$= \frac{1}{3} . a^{2} .3 a = a^{3}$

Câu 22. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng (ABCD). Đường thẳng SC tạo với đáy góc $45 °$ . Gọi M, N lần lượt là trung điểm của AB và AD. Thể tích của khối chóp S.MCDN là:

A. $\frac{5 a^{3} \sqrt{2}}{12}$

B. $\frac{5 a^{3} \sqrt{2}}{6}$

C. $\frac{5 a^{3} \sqrt{2}}{8}$

D. $\frac{5 a^{3} \sqrt{2}}{24}$

Hiển thị đáp án

Đáp án: D

Giải thích:

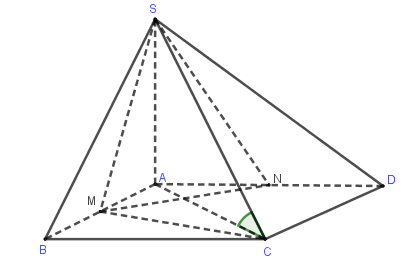
Trắc nghiệm Ôn tập Chương I - Khối đa diện có đáp án - Toán lớp 12 (ảnh 17)

$\begin{matrix} (S A B) ⊥ (A B C D) \\ (S A D) ⊥ (A B C D) \\ (S A B) \cap (S A D) = S A \end{matrix}\} \Rightarrow S A ⊥ (A B C D)$

$\Rightarrow A C$ là hình chiếu vuông góc của SC trên (ABCD)

$\Rightarrow (\hat{S C; (A B C D)}) = (\hat{S C; A C}) = \hat{S C A} = 45 °$

(vì $S A ⊥ (A B C D) \Rightarrow S A ⊥ A C \Rightarrow Δ S A C$

vuông tại A $\Rightarrow \hat{S C A} < 90 °$ )

$\Rightarrow S A = A C = a \sqrt{2}$

$S_{A B C D} = a^{2}$

$S_{A M N} = \frac{1}{2} A M . A N = \frac{1}{2} . \frac{a}{2} . \frac{a}{2} = \frac{a^{2}}{8}$

$S_{B C M} = \frac{1}{2} B M . B C = \frac{1}{2} . \frac{a}{2} . a = \frac{a^{2}}{4}$

$\Rightarrow S_{M C D N} = S_{A B C D} - S_{A M N} - S_{B C M}$

$= a^{2} - \frac{a^{2}}{8} - \frac{a^{2}}{4} = \frac{5 a^{2}}{8}$

$\Rightarrow V_{S . M C D N} = \frac{1}{3} S A . S_{M C D N}$

$= \frac{1}{3} a \sqrt{2} . \frac{5 a^{2}}{8} =$ $\frac{5 a^{3} \sqrt{2}}{24}$

Câu 23. Cho khối lăng trụ tam giác đều $A B C . A_{1} B_{1} C_{1}$ có tất cả các cạnh bằng a. Gọi M là trung diểm của $A A_{1}$ . Thể tích khối chóp $M . B C A_{1}$ là:

A. $\frac{a^{3} \sqrt{3}}{12}$

B. $\frac{a^{3} \sqrt{3}}{24}$

C. $\frac{a^{3} \sqrt{3}}{6}$

D. $\frac{a^{3} \sqrt{3}}{8}$

Hiển thị đáp án

Đáp án: B

Giải thích:

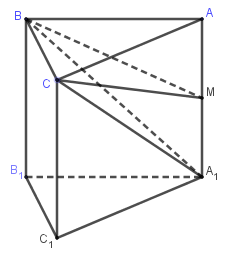
$Δ A B C$ là tam giác đều cạnh a nên có diện tích $S_{A B C} = \frac{a^{2} \sqrt{3}}{4}$

Ta có: $A M = \frac{A A_{1}}{2} = \frac{a}{2}$

Hai tứ diện MABC và $M A_{1} B C$ có chung đỉnh C, diện tích hai đáy $M A B$ và $M A_{1} B$ bằng nhau nên có thể tích bằng nhau. Suy ra:

$V_{M . B C A_{1}} = V_{M . A B C}$

$= \frac{1}{3} A M . S_{A B C} = \frac{a^{3} \sqrt{3}}{24}$

Câu 24. Cho hình lăng trụ $A B C . A' B' C'$ có thể tích bằng V. gọi M là trung điểm cạnh BB’, điểm N thuộc cạnh CC’ sao cho $C N = 2 C' N$ . Tính thể tích khối chóp A.BCNM theo V

A. $V_{A . B C N M} = \frac{7 V}{12}$

B. $V_{A . B C N M} = \frac{7 V}{18}$

C. $V_{A . B C N M} = \frac{V}{3}$

D. $V_{A . B C N M} = \frac{5 V}{18}$

Hiển thị đáp án

Đáp án: B

Giải thích:

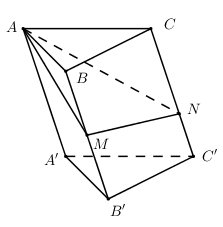
Ta có:

$S_{B C C' B'} = d (B; C C') . C C'$

$S_{B M N C} = \frac{(B M + C N) d (B; C C')}{2}$

$= \frac{1}{2} d (B; C C') (\frac{1}{2} C C' + \frac{2}{3} C C')$

$= \frac{7}{12} d (B; C C') . C C'$

$\Rightarrow \frac{S_{B M N C}}{S_{B C C' B'}} = \frac{7}{12} \Rightarrow \frac{V_{A . B M N C}}{V_{A . B C C' B'}} = \frac{7}{12}$

$\Rightarrow V_{A . B M N C} = \frac{7}{12} V_{A . B C C' B'}$

Mà $V_{A . B C C' B'} = \frac{2}{3} V$

$\Rightarrow V_{A . B M N C} = \frac{7}{12} . \frac{2}{3} V = \frac{7}{18} V$

Câu 25. Cho hình chóp đều S.ABCD có diện tích đáy là $16 c m^{2}$ , diện tích một mặt bên là $8 \sqrt{3} c m^{2}$ . Thể tích khối chóp S.ABCD là:

A. $\frac{32 \sqrt{2}}{3} c m^{3}$

B. $\frac{32 \sqrt{13}}{3} c m^{3}$

C. $\frac{32 \sqrt{11}}{3} c m^{3}$

D. $4 c m^{3}$

Hiển thị đáp án

Đáp án: C

Giải thích:

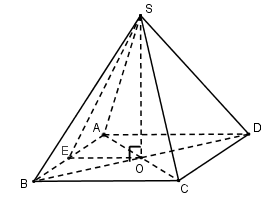
Gọi $O = A C \cap B D$ .

Vì chóp S.ABCD đều nên $S O ⊥ (A B C D)$

Vì chóp S.ABCD đều nên ABCD là hình vuông

$\Rightarrow S_{A B C D} = A B^{2} = 16$

$\Rightarrow A B = 4 (c m) = A D$

Gọi E là trung điểm của AB

$\Rightarrow$ OE là đường trung bình của tam giác ABD

$\Rightarrow O E / / A D \Rightarrow O E ⊥ A B$

và $O E = \frac{1}{2} A D = \frac{1}{2} .4 = 2 (c m)$

$\begin{matrix} O E ⊥ A B \\ S O ⊥ A B (S O ⊥ (A B C D)) \end{matrix}\}$

$\Rightarrow A B ⊥ (S O E) \Rightarrow A B ⊥ S E$

$\Rightarrow S_{Δ S A E} = \frac{1}{2} S E . A B = 8 \sqrt{3}$

$\Rightarrow S E = \frac{16 \sqrt{3}}{A B} = \frac{16 \sqrt{3}}{4} = 4 \sqrt{3}$

$S O ⊥ (A B C D) \Rightarrow S O ⊥ O E \Rightarrow Δ S O E$

vuông tại O

$\Rightarrow S O = \sqrt{S E^{2} - O E^{2}}$

$= \sqrt{48 - 4} = \sqrt{44} = 2 \sqrt{11} (c m)$

Vậy $V_{S . A B C D} = \frac{1}{3} S O . S_{A B C D}$

$= \frac{1}{3} .2 \sqrt{11} .16 = \frac{32 \sqrt{11}}{3} (c m^{3})$

Câu 26. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và mặt bên hợp với đáy một góc $60 °$ . Thể tích khối chóp S.ABC là:

A. $\frac{a^{3} \sqrt{3}}{12}$

B. $\frac{a^{3} \sqrt{2}}{24}$

C. $\frac{a^{3} \sqrt{3}}{24}$

D. $\frac{a^{3}}{24}$

Hiển thị đáp án

Đáp án: C

Giải thích:

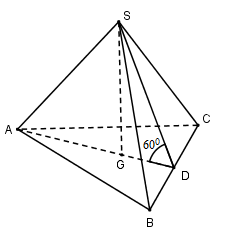
Gọi G là trọng tâm tam giác ABC.

Vì chóp S.ABC đều nên $S G ⊥ (A B C)$

Gọi D là trung điểm của BC ta có: $A D ⊥ B C$

Ta có:

$\begin{matrix} B C ⊥ A D \\ B C ⊥ S G (S G ⊥ (A B C)) \end{matrix}\}$

$\Rightarrow B C ⊥ (S A D) \Rightarrow B C ⊥ S D$

$\begin{matrix} (S B C) \cap (A B C) = B C \\ (S B C) \supset S D ⊥ B C \\ (A B C) \supset A D ⊥ B C \end{matrix}\}$

$\Rightarrow (\hat{(S B C); (A B C)}) = (\hat{S D; A D})$

$= \hat{S A D} = 60 °$

Vì tam giác ABC đều cạnh a nên

$A D = \frac{a \sqrt{3}}{2} \Rightarrow D G = \frac{1}{3} A D = \frac{a \sqrt{3}}{6}$

$S G ⊥ (A B C) \Rightarrow S G ⊥ A D \Rightarrow Δ S G D$ vuông tại G

$\Rightarrow S G = G D . \tan 60 = \frac{a \sqrt{3}}{6} . \sqrt{3} = \frac{a}{2}$

Tam giác ABC đều

$\Rightarrow S_{Δ A B C} = \frac{a^{2} \sqrt{3}}{4}$

$\Rightarrow V_{S . A B C} = \frac{1}{3} S G . S_{Δ A B C}$

$= \frac{1}{3} . \frac{a}{2} . \frac{a^{2} \sqrt{3}}{4} = \frac{a^{3} \sqrt{3}}{24}$

Câu 27. Cho hình chóp tứ giác đều S.ABCD có chiều cao h, góc ở đỉnh của mặt bên bằng $60 °$ . Thể tích hình chóp là:

A. $\frac{3 h^{2}}{2}$

B. $\frac{h^{3}}{3}$

C. $\frac{3 h^{3}}{3}$

D. $\frac{h^{3} \sqrt{3}}{3}$

Hiển thị đáp án

Đáp án: C

Giải thích:

Gọi $O = A C \cap B D$

Vì chóp S.ABCD đều nên $S O ⊥ (A B C D)$

Đặt $S A = S B = S C = S D = a$

Tam giác SCD có: $S C = S D; \hat{C S D} = 60 °$

$\Rightarrow Δ S C D$ đều

$\Rightarrow C D = S C = S D = a$

$\Rightarrow$ Hình vuông ABCD cạnh a

$\Rightarrow A C = B D = a \sqrt{2}$

$\Rightarrow O C = \frac{1}{2} A C = \frac{a \sqrt{2}}{2}$

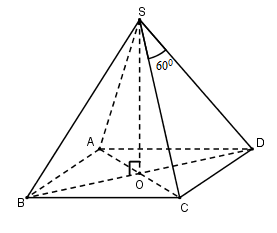
Trắc nghiệm Ôn tập Chương I - Khối đa diện có đáp án - Toán lớp 12 (ảnh 22)

$S O ⊥ (A B C D) \Rightarrow S O ⊥ O C \Rightarrow Δ S O C$ vuông tại O.

$\Rightarrow S O = \sqrt{S C^{2} - O C^{2}}$

$\to h = \sqrt{a^{2} - \frac{a^{2}}{2}} = \frac{a \sqrt{2}}{2}$

$\Rightarrow S_{A B C D} = a^{2} = {(h \sqrt{2})}^{2} = 2 h^{2}$

Vậy $V_{S . A B C D} = \frac{1}{3} S O . S_{A B C D}$

$= \frac{1}{3} h .2 h^{2} = \frac{2 h^{3}}{3}$

Câu 28. Trong các mệnh đề sau mệnh đề nào sai:

A. Hình lăng trụ đều có cạnh bên vuông góc với đáy.

B. Hình lăng trụ đều có các mặt bên là các hình chữ nhật.

C. Hình lăng trụ đều có các cạnh bên bằng đường cao của lăng trụ.

D. Hình lăng trụ đều có tất cả các cạnh đều bằng nhau

Hiển thị đáp án

Đáp án: D

Giải thích:

Phương án A. Đúng: Vì hình lăng trụ đều là hình lăng trụ đứng có đáy là đa giác đều nên lăng trụ đều có cạnh bên vuông góc với đáy.

Phương án B. Đúng.

Phương án C. Đúng.

Phương án D. Sai: Do lăng trụ đều có cạnh đáy và chiều cạnh bên có thể không bằng nhau.

Câu 29. Mỗi hình dưới đây gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó).

Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Số đa diện lồi trong các hình vẽ trên là:

A. 1

B. 2

C. 3

D. 4

Hiển thị đáp án

Đáp án: B

Giải thích: Hai đa diện lồi là hình 1 và 4.

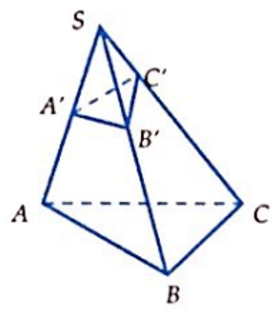
Câu 30. Cho khối chóp S.ABC có SA = 9, SB = 4, SC = 8 và đôi một vuông góc. Các điểm A', B', C' thỏa mãn SA→ = 2SA'→, SB→ = 3SB'→, SC→ = 4SC'→. Thể tích khối chóp S.A'B'C' là:

A. 24

B. 16

C. 2

D. 12

Hiển thị đáp án

Đáp án: C

Giải thích:

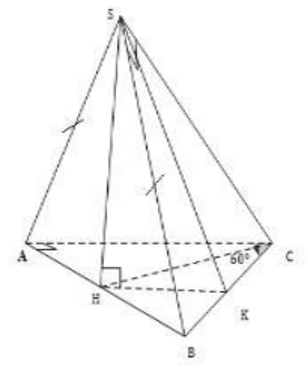
Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Câu 31. Cho hình chóp S.ABC có đáy là tam giác vuông tại A, các cạnh AB = 1, AC = 2. Các tam giác SAB và SAC lần lượt vuông tại B và C. Góc giữa (SBC) và mặt phẳng đáy bằng 60° . Tính thể tích của khối chóp đã cho.

Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Hiển thị đáp án

Đáp án: B

Giải thích:

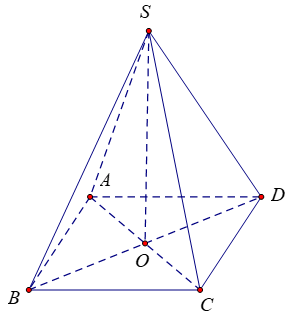
Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Câu 32. Cho khối chóp tứ giác đều S.ABCD có cạnh bằng a, cạnh bên SC tạo với mặt đáy một góc 45°. Tính thể tích của khối chóp S. ABCD

Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Hiển thị đáp án

Đáp án: B

Giải thích:

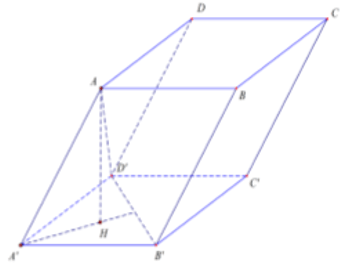
Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Câu 33. Tính thể tích của hình hộp ABCD.A'B'C'D' biết rằng AA'B'D' là tứ diện đều cạnh bằng a.

Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Hiển thị đáp án

Đáp án: A

Giải thích:

Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Câu 34. Cho hình chóp tam giác đều cạnh bằng 3. Tính thể tích hình chóp đó biết chiều cao

h = 7

Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Hiển thị đáp án

Đáp án: A

Giải thích:

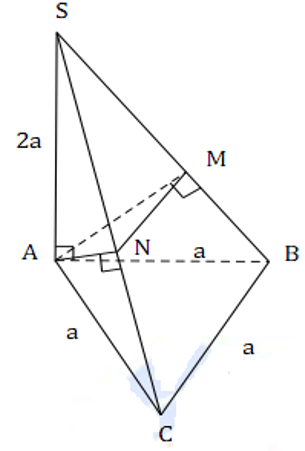
Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Câu 35. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, SA = 2a và SA vuông góc với mặt phẳng (ABC). Gọi M và N lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB và SC. Thể tích V của khối chóp A.BCNM bằng

Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Hiển thị đáp án

Đáp án: A

Giải thích:

Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Câu 36. Cho tứ diện ABCD. Gọi B’ và C’ lần lượt là trung điểm của AB và AC. Khi đó tỉ số thể tích của khối tứ điện AB’C’D và khối tứ diện ABCD bằng:

Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Hiển thị đáp án

Đáp án: B

Giải thích:

Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Câu 37. Kim tự tháp Kê-ốp ở Ai Cập được xây dựng vào khoảng 2500 năm trước công nguyên. Kim tự tháp này là một hình chóp tứ giác đều có chiều cao là 147m, cạnh đáy dài 230m. Tính thể tích của nó

A. 2 592 100m³

B. 52900 m³

C. 7776300 m³

D. 1470000 m³

Hiển thị đáp án

Đáp án: A

Giải thích:

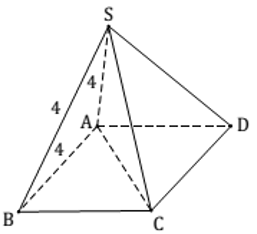
Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Câu 38. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và thể tích V = 12 cm³. Mặt bên SAB là tam giác đều cạnh bằng 4cm. Tính khoảng cách từ C đến mặt phẳng (SAB).

Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Hiển thị đáp án

Đáp án: B

Giải thích:

Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Câu 39. Cho hình chóp S.ABC có tam giác ABC vuông tại A, BC = 2a; 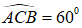Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12 . Mặt phẳng (SAB) vuông góc với mặt phẳng (ABC), tam giác SAB cân tại S, tam giác SBC vuông tại S. Thể tích khối chóp S.ABC là:

Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Hiển thị đáp án

Đáp án: B

Giải thích:

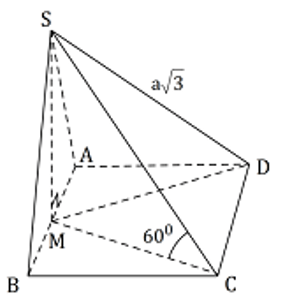
Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Câu 40. Cho hình chóp S.ABCD có đáy là hình vuông, gọi M là trung điểm của AB. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết SD = a√3, SC tạo với mặt phẳng đáy (ABCD) một góc 60°. Thể tích khối chóp S.ABCD theo a là

Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Hiển thị đáp án

Đáp án: B

Giải thích:

Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Các câu hỏi trắc nghiệm Toán lớp 12 có đáp án, chọn lọc khác:

Trắc nghiệm Khái niệm về mặt tròn xoay có đáp án

Trắc nghiệm Mặt cầu có đáp án

Trắc nghiệm Ôn tập Chương 2 - Mặt nón. Mặt trụ. Mặt cầu có đáp án

Trắc nghiệm Hệ tọa độ trong không gian có đáp án

Trắc nghiệm Phương trình mặt phẳng có đáp án

1 1,476 22/12/2023

Tải về

Trang trước

Trang sau

Xem thêm các chương trình khác:

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3