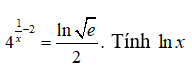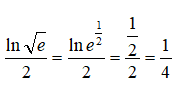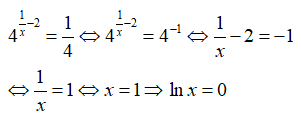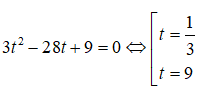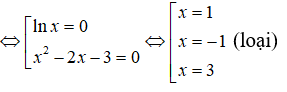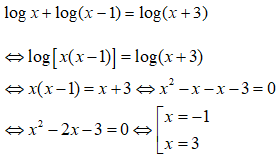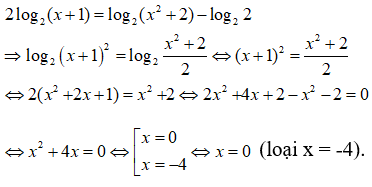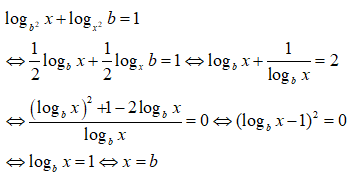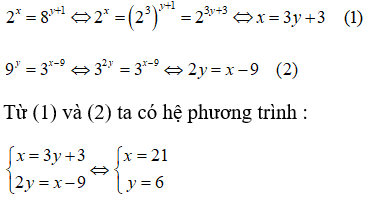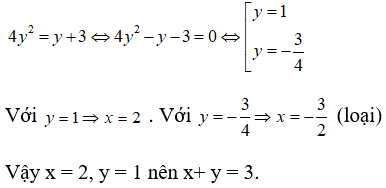TOP 40 câu Trắc nghiệm Phương trình mũ và phương trình Logarit (có đáp án 2024) - Toán 12
Bộ 40 câu hỏi trắc nghiệm Toán lớp 12 Bài 5: Phương trình mũ và phương trình Logarit có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 12 Bài 5.
Trắc nghiệm Toán 12 Bài 5: Phương trình mũ và phương trình Logarit
Bài giảng Trắc nghiệm Toán 12 Bài 5: Phương trình mũ và phương trình Logarit
Câu 1. Phương trình 42x+5=22−x có nghiệm là:
A. −85
B. 3
C. 85
D. 125
Đáp án: A
Giải thích:
⇔24x+10=22−x
⇔4x+10=2−x
⇔x=−85
Câu 2. Tổng các nghiệm của phương trình 3x4−3x2=81
A. 0
B. 1
C. 3
D. 4
Đáp án: A
Giải thích:
⇔x4−3x2−4=0
⇔x2=4⇔x=±2
Tổng các nghiệm sẽ bằng 0
Câu 3. Giải phương trình 4x=8x−1
A. x=−3
B. x=−2
C. x=2
D. x=3
Đáp án: D
Giải thích:
4x=8x−1
⇔22x=23(x−1)
⇔2x=3(x−1)
⇔x=3
Câu 4. Phương trình 2x−1−2x2−x=(x−1)2 có tất cả bao nhiêu nghiệm?
A. 1.
B. 2
C. 3
D. 4
Đáp án: A
Giải thích:
Phương trình
2x−1−2x2−x=(x−1)2
⇔2x−1+(x−1)=2x2−x+(x2−x).(*)
Xét hàm số f(t)=2t+t trên ℝ, ta có f'(t)=2tln2+1>0,∀t∈ℝ.
Suy ra hàm số f(t) đồng biến trên ℝ.
Nhận thấy (*) có dạng f(x−1)=f(x2−x)
⇔x−1=x2−x
⇔(x−1)2=0⇔x=1.
Vậy phương trình có một nghiệm duy nhất x=1.
Câu 5. Số nghiệm của phương trình log4(log2x)+log2(log4x)=2 là:
A. 0
B. 1
C. 2
D. Nhiều hơn 2.
Đáp án: B
Giải thích:
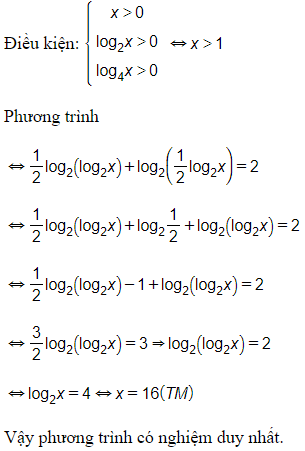
Câu 6. Giải phương trình log4(x+1)+log4(x−3)=3
A. x=1±2√17
B. x=1+2√17
C. x=33
D. x=5
Đáp án: B
Giải thích:
Điều kiện: {x+1>0x−3>0⇔x>3
Ta có:
log4(x+1)+log4(x−3)=3
⇔log4(x+1)(x−3)=3
⇔(x+1)(x−3)=43
⇔x2−2x−67=0
=x=1±2√17
So sánh với điều kiện nghiệm của pt là x=1±2√17
Câu 7. Tổng lập phương các nghiệm của phương trình log2x.log3(2x−1)=2log2x bằng:
A. 6
B. 26
C. 126
D. 216
Đáp án: C
Giải thích:
Điều kiện: x>12
Phương trình đã cho
⇔log2x.[log3(2x−1)−2]=0
⇔[log2x=0log3(2x−1)=2
⇔[x=12x−1=9
⇔[x=1(TM)x=5(TM)
⇒13+53=126
Câu 8. Tính tổng tất cả các nghiệm của phương trình 2017sin2x−2017cos2x=cos2x trên đoạn [0;π].
A. x=π.
B. x=π4.
C. x=π2.
D. x=3π4.
Đáp án: A
Giải thích:
Phương trình
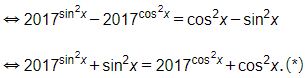
Xét hàm số f(t)=2017t+t trên ℝ, ta có f'(t)=2017tln2017+1>0,∀t∈ℝ.
Suy ra hàm số f(t) đồng biến trên ℝ.
Nhận thấy (*) có dạng f(sin2x)=f(cos2x)
⇔sin2x=cos2x
⇔cos2x−sin2x=0
⇔cos2x=0
⇔x=π4+kπ2, k∈ℤ.
Vì x∈[0;π]
→x={π4;3π4}
→T=π4+3π4=π.
Câu 9. Phương trình 4x2+x+2x2+x+1−3=0 có bao nhiêu nghiệm không âm?
A. 0.
B. 1.
C. 2.
D. 3.
Đáp án: B
Giải thích:
Phương trình tương đương với 4x2+x+2.2x2+x−3=0.
Đặt t=2x2+x, t>0. Phương trình trở thành t2+2t−3=0
⇔[t=1t=−3 (loai)
Với t=1, ta được 2x2+x=1
⇔x2+x=0
⇔[x=0x=−1
Vậy chỉ có duy nhất nghiệm x=0 là nghiệm không âm.
Câu 10. Tập nghiệm của phương trình log2(x2−1)=log22x là:
A. {1+√22}
B. {2;41}
C. {1−√2;1+√2}
D. {1+√2}
Đáp án: D
Giải thích:
Điều kiện: {x2−1>02x>0⇔x>1
Với điều kiện này thì phương trình đã cho tương đương với
x2−1=2x
⇔x2−2x−1=0
⇔[x=1+√2(tm)x=1−√2(ktm)
Vậy tập nghiệm của phương trình đã cho là {1+√2}
Câu 11. Tính tổng tất cả các nghiệm của phương trình 4tan2x+21cos2x−3=0 trên đoạn [0;3π].
A. T=π.
B. T=3π2.
C. T=6π.
D. T=0.
Đáp án: C
Giải thích:
Điều kiện: {cosx≠0x∈[0;3π]
⇔x≠{π2;3π2;5π2}.
Ta có 4tan2x+21cos2x−3=0
⇔(2tan2x)2+2tan2x+1−3=0
⇔(2tan2x)2+2.2tan2x−3=0
⇔[2tan2x=12tan2x=−3 (loai)
⇔2tan2x=1
⇔tan2x=0
⇔x=kπ,k∈ℤ.
Vì 0≤x≤3π
→x={0; π; 2π; 3π} (thỏa mãn)
→T=6π.
Câu 12. Tính P là tích tất cả các nghiệm của phương trình log12x2−3x+2x=0
A. P = 4
B. P = 2√2
C. P = 2
D. P = 1
Đáp án: C
Giải thích:
Điều kiện: x2−3x+2x>0
Phương trình đã cho
⇔x2−3x+2x=1
⇔x2−4x+2=0
⇔[x=2−√2=x1x=2+√2=x2 (tm)
⇒P=x1x2
=(2−√2)(2+√2)
=4−2=2
Câu 13. Biết rằng phương trình 2log(x+2)+log4=logx+4log3 có hai nghiệm phân biệt x1,x2(x1<x2). Tính P=x1x2
A. P = 4
B. P = 14
C. P = 64
D. P = 164
Đáp án: D
Giải thích:
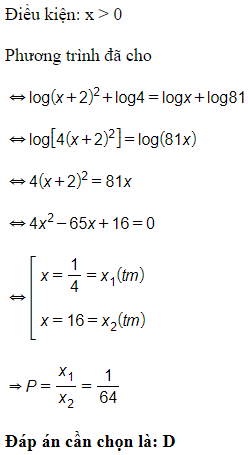
Câu 14. Giải phương trình log3(2x−1)=2, ta có nghiệm là:
A. x=15
B. x=15
C. x=25
D. x=5
Đáp án: D
Giải thích:
Điều kiện: x > 12
⇔2x−1=32
⇔2x=10
⇔x=5 (tm)
Câu 15. Tập nghiệm của phương trình log2(x2−x+2)=1
A. {0}
B. {0;1}
C. {−1;0}
D. {1}
Đáp án: B
Giải thích:
Điều kiện: x2−x+2>0 (luôn đúng với mọi x)
Khi đó phương trình tương đương:
x2−x+2=2
⇔x2−x=0
⇔[x=0x=1
Vậy tập nghiệm của phương trình là: S={0;1}
Câu 16. Tính tổng T tất cả các nghiệm của phương trình
A. T = 2
B. T = 3
C. T = 134
D. T = 14
Đáp án: A
Giải thích:
⇔4−13.(23)x+9.(23)2x=0
⇔[(23)x=1(23)x=49
⇔[x=0x=2
⇒T=0+2=2
Câu 17. Giải phương trình √3x+6=3x có tập nghiệm bằng:
A. {1;log32}
B. {−2;3}
C. {1}
D. {3}
Đáp án: C
Giải thích:
Đặt t=3x,t>0
⇒√t+6=t
→t+6=t2
⇒[t=−2(l)t=3
t=3⇒3x=3
⇒x=1
Câu 18. Khi đặt 3x=t thì phương trình 9x+1−3x+1−30=0 trở thành:
A. 3t2−t−10=0
B. 9t2−3t−10=0
C. t2−t−10=0
D. 2t2−t−1=0
Đáp án: A
Giải thích:
Ta có: 9x+1−3x+1−30=0
⇔9.9x−3.3x−30=0
⇔3.(3x)2−3x−10=0 (*)
Đặt 3x=t ta có phương trình (*) ⇔3t2−t−10=0
Câu 19. Tìm tích các nghiệm của phương trình (√2−1)x+(√2+1)x−2√2=0
A. 2
B. – 1
C. 0
D. 1
Đáp án: B
Giải thích:
Đặt t=(√2−1)x(t>0) phương trình có dạng
t+1t=2√2
⇔t2−2√2t+1=0
⇔[t=√2+1(tm)t=√2−1(tm)
Khi đó:
t=√2+1⇒x=−1
t=√2−1⇒x=1
Suy ra tích các nghiệm bằng – 1.
Câu 20. Giải phương trình log3(x+2)+log9(x+2)2=54
A. x=1
B. x=8√35−2
C. x=4√35−2
D. x=4√3−2
Đáp án: B
Giải thích:
log3(x+2)+log9(x+2)2=54 (*)
ĐKXĐ: x > - 2.
⇔log3(x+2)+log3(x+2)=54(*)
⇔log3(x+2)=58
⇔x+2=358
⇔x=8√35−2 (tm)
Câu 21. Phương trình log2(x−3)+2log43.log3x=2 có tất cả bao nhiêu nghiệm?
A. 1
B. 2
C. 3
D. 0
Đáp án: A
Giải thích:
Điều kiện: {x−3>0x>0⇔x>3
Phương trình đã cho
log2(x−3)+2log4x=2
⇔log2(x−3)+log2x=2
⇔log2[(x−3)x]=2
⇔(x−3)x=22
⇔x2−3x−4=0
⇔[x=−1(l)x=4(tm)
Câu 22. Số nghiệm thực phân biệt của phương trình 4x2−5.2x2+4=0 là:
A. 3
B. 2
C. 0
D. 1
Đáp án: A
Giải thích:
4x2−5.2x2+4=0
⇔(2x2)2−5.2x2+4=0
⇔(2x2−4)(2x2−1)=0
⇔[2x2=42x2=1
⇔[x2=2x2=0
⇔[x=±√2x=0
Câu 23. Giải phương trình log2(2x−1).log4(2x+1−2)=1. Ta có nghiệm:
A. x=log23 và x=log25
B. x=1 và x=−2
C. x=log23 và x=log254
D. x=1 và x=2
Đáp án: C
Giải thích:
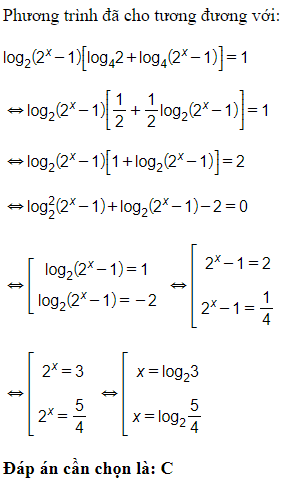
Câu 24. Cho a, b, x là các số thực dương khác 1 thỏa : 4log2ax+3log2bx=8logax.logbx (1). Mệnh đề (1) tương đương với mệnh đề nào sau đây:
A. a=b2
B. a=b2 hoặc a3=b2
C. a3=b2
D. x=ab
Đáp án: B
Giải thích:
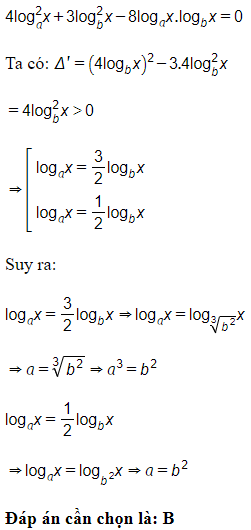
Câu 25. Tìm m để phương trình 4x−2x+3+3=m có đúng 2 nghiệm x∈(1;3)
A. −13<m<−9
B. 3<m<9
C. −9<m<3
D. −13<m<3
Đáp án: A
Giải thích:
Đặt t=2x;x∈(1;3)
⇒t=2x∈(2;8)
Xét hàm số y=t2−8t+3 trên (2; 8) có:
y'=2t−8;y'=0
⇔2t−8=0
⇔t=4∈(2;8)
Bảng biến thiên:
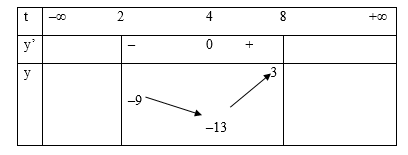
Căn cứ bảng biến thiên:
Phương trình 4x−2x+3+3=m có đúng 2 nghiệm x∈(1;3)⇔−13<m<−9
Câu 26. Tìm giá trị của tham số m để phương trình 9x−m.3x+2+9m=0 có hai nghiệm phân biệt x1;x2 thỏa mãn x1+x2=3
A. m=4
B. m=1
C. m=52
D. m=3
Đáp án: D
Giải thích:
Phương trình tương đương với: 32x−9m.3x+9m=0 (*)
Đặt 3x=a với a > 0 phương trình thành: a2−9m.a+9m=0
Giả sử phương trình có 2 nghiệm x1 và x2 thì 3x1;3x2 lần lượt là nghiệm của (*)
Suy ra: 3x1.3x2=9m
⇔3x1+x2=9m
⇔x1+x2=log39m=3
⇒9m=27⇔m=3
Câu 27. Tính tổng T tất cả các nghiệm của phương trình 5sin2x+5cos2x=2√5 trên đoạn [0;2π]
A. T=π
B. T=3π4
C. T=2π
D. T=4π
Đáp án: D
Giải thích:
Ta có: 5sin2x+5cos2x=2√5
⇔5sin2x+51−sin2x=2√5
⇔5sin2x+55sin2x=2√5
⇔(5sin2x)2−2√5.5sin2x+5=0
⇔(5sin2x−√5)2=0
⇔5sin2x−√5=0
⇔5sin2x=512
⇔sin2x=12
⇔[sinx=√22sinx=−√22
⇔x=π4+kπ2,k∈Z
Do x∈[0;2π]
⇒x={π4;3π4;5π4;7π4}
Câu 28. Số nghiệm thực phân biệt của phương trình 2x+14x+2x4+1x=4 là:
A. 1
B. 2
C. 3
D. 0
Đáp án: D
Giải thích:
Điều kiện: x≠0
Với x < 0 ta có: {x+14x<0x4+1x<0
⇒{2x+14x<12x4+1x<1
⇒2x+14x+2x4+1x<2
⇒ Phương trình không có nghiệm x < 0.
Với x > 0, áp dụng bất đẳng thức Cô si cho hai số dương ta được:
{x+14x≥2√x.14xx4+1x≥2√x4.1x
⇒{2x+14x≥22x4+1x≥2
⇒2x+14x+2x4+1x≥4
Dấu “=” xảy ra khi và chỉ khi:
{x=14xx2=4 (không xảy ra)
Vậy 2x+14x+2x4+1x>4 nên phương trình vô nghiệm.
Câu 29. Tìm giá trị m để phương trình 2|x−1|+1+2|x−1|+m=0 có nghiệm duy nhất
A. m=3
B. m=18
C. m=−3
D. m=1
Đáp án: C
Giải thích:
Đặt |x−1|=a khi đó phương trình trở thành 2a+1+2a+m=0 (1)
Để phương trình đã cho có nghiệm duy nhất thì pt (1) bắt buộc phải có nghiệm duy nhất a = 0 (vì nếu a > 0 thì sẽ tồn tại 2 giá trị của x)
Nên 21+20+m=0
⇒m=−3
Câu 30. Tìm tất cả các giá trị thực của m để phương trình 2log2|x|+log2|x+3|=m có 3 nghiệm thực phân biệt:
A. m∈(0;2)
B. m∈{0;2}
C. m∈(−∞;2)
D. m∈{2}
Đáp án: D
Giải thích:
TXĐ: D = R
2log2|x|+log2|x+3|=m
⇔log2|x|2+log2|x+3|=m
⇔log2(|x|2.|x+3|)=m
⇔|x|2.|x+3|=2m
⇔x2.|x+3|=2m
Xét hàm f(x)=x2.|x+3|
ta có: f(x)=x2.|x+3|
=|x3+3x2|
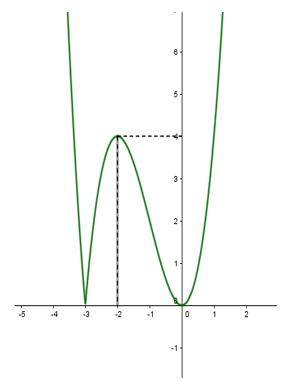
Để phương trình có 3 nghiệm phân biệt thì 2m=4⇔m=2
Câu 31. Giả sử x là nghiệm của phương trình
A. 0
B. ln3
C. –ln3
D. 1/ln3
Đáp án: A
Giải thích:
Để ý rằng
nên phương trình đã cho tương đương với
Chọn đáp án A.
Câu 32. Tính tích tất cả các nghiệm của phương trình 32x2 + 2x + 1 - 28.3x2 + x + 9 = 0
A. -4
B. -2
C. 2
D. 4
Đáp án: B
Giải thích:
Ta có: 32x2 + 2x + 1 -28.3x2 + x + 9 = 0 ⇔ 3.32(x2 + x) - 28.3x2 + x + 9 = 0
Đặt t = 3x2 + x > 0 nhận được phương trình
Với t = 1/3 = 3-1 được 3x2 + x = 3-1 ⇔ x2 + x + 1 = 0(vô nghiệm)
Với t = 9 được phương trình 3x2 + x = 9 = 32 ⇔ x2 + x = 2
x2 + x - 2 = 0 ⇔ x -2 hoặc x = 1
Tích của hai nghiệm này bằng -2.
Chọn đáp án B
Câu 33. Giải phương trình (x2 - 2x)lnx = lnx3
A. x = 1, x = 3
B. x = -1, x = 3
C. x = ±1, x = 3
D. x = 3
Đáp án: A
Giải thích:
Điều kiện x > 0. Khi đó phương trình đã cho tương đương với
(x2 -2x)lnx = 3lnx ⇔ (x2 - 2x + 3)lnx = 0
Vậy phương trình có hai nghiệm là x = 1, x = 3 .
Chọn đáp án A.
Chú ý. Sai lầm thường gặp là quên điều kiện dẫn đến không loại được nghiệm x = -1 và chọn phương án nhiễu C.
Thậm chí, có thể học sinh biến đổi (x2 - 2x)lnx = 3lnx ⇔ x2 -2x = 3(giản ước cho lnx) dẫn đến mất nghiệm x = 1 và chọn phương án nhiễu D.
Câu 34. Giải phương trình logx = log(x + 3) - log(x - 1)
A. x = 1
B. x = 3
C. x = 4
D. x = -1, x = 3
Đáp án: B
Giải thích:
Điều kiện x > 1. Khi đó phương trình tương đương với
Loại nghiệm x = -1 do không thỏa mãn điều kiện. Phương trình có một nghiệm x = 3.
Chọn đáp án B.
Chú ý: Cũng như ở ví dụ 5, sai lầm học sinh dễ gặp bài này là do chủ quan muốn tiết kiệm thời gian mà quên đặt điều kiện, dẫn tới không loại được nghiệm x = -1 và chọn phương án nhiễu D.
Câu 35. Giải phương trình log√2(x + 1) = log2(x2 + 2) - 1
A. x = 1
B. x = 0
C. x = 0, x = -4
D. x = 0, x = 1
Đáp án: B
Giải thích:
Điều kiện x > -1. Khi đó phương trình tương đương với
2log2(x + 1) = log2(x2 + 2)
Câu 36. Cho biết logb2x + logx2b = 1, b > 0, b ≠ 1, x ≠ 1. Khi đó x bằng:
A. b
B. √b
C. 1/b
D. 1/b2
Đáp án: A
Giải thích:
Điều kiện: x > 0
Chọn đáp án A.
Chú ý. Khác với các ví dụ trên, các biến đổi trong ví dụ này không làm mở rộng miền xác định của phương trình (x > 0). Do đó ta đã không nhất thiết phải đặt điều kiện x > 0. Trong nhiều trường hợp việc bỏ qua đặt điều kiện sẽ làm đơn giản hơn và tiết kiệm thời gian.
Câu 37. Cho biết 2x = 8y + 1 và 9y = 3x - 9 . Tính giá trị của x + y
A. 21
B. 18
C. 24
D. 27
Đáp án: D
Giải thích:
Vậy x + y =27.
Chọn đáp án D.
Câu 38. Giả sử x, y là hai số thực thỏa mãn đồng thời 3x2 - 2xy = 1 và 2log3x = log3(y + 3). Tính x + y
A. 9/4
B. 3/2
C. 3
D. 9
Đáp án: C
Giải thích:
Điều kiện x > 0, y > -3.
Ta có: 3x2 - 2xy = 1 = 30 ⇔ x2 - 2xy = 0
⇔ x(x - 2y) = 0 ⇔ x - 2y = 0 (x > 0) ⇔ x = 2y (1)
2log3x = log3( y + 3) ⇔ log3x2 = log3(y + 3) ⇔ x2 = y + 3 (2)
Thế (1) vào (2) ta được:
Câu 39. Giải phương trình 10x = 0,00001
A. x = -log4
B. x = -log5
C. x = -4
D. x = -5
Đáp án: D
Giải thích:
10x = 0,00001 ⇔ 10x = 10-5 ⇔ x = -5
Câu 40. Tính tổng bình phương các nghiệm của phương trình 4x2 + 2 - 9.2x2 + 2 + 8 = 0
A. 2
B. 4
C. 17
D. 65
Đáp án: A
Giải thích:
Các câu hỏi trắc nghiệm Toán lớp 12 có đáp án, chọn lọc khác:
Trắc nghiệm Bất phương trình mũ và bất phương trình Logarit có đáp án
Trắc nghiệm Ôn tập Chương 2 có đáp án
Trắc nghiệm Nguyên hàm có đáp án
Xem thêm các chương trình khác:
- Trắc nghiệm Sinh học lớp 7 có đáp án
- Trắc nghiệm Toán lớp 7 có đáp án
- Trắc nghiệm Ngữ văn lớp 7 có đáp án
- Trắc nghiệm Sinh học 8 có đáp án
- Trắc nghiệm Toán lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn 8 có đáp án
- Trắc nghiệm Hóa học lớp 8 có đáp án
- Trắc nghiệm Địa Lí lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Tiếng Anh lớp 8 có đáp án
- Trắc nghiệm GDCD lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Lịch sử lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Vật Lí lớp 8 có đáp án
- Trắc nghiệm Công nghệ lớp 8 có đáp án
- Trắc nghiệm Tin học lớp 8 có đáp án
- Trắc nghiệm Sinh học lớp 9 có đáp án
- Trắc nghiệm Toán lớp 9 có đáp án
- Trắc nghiệm Ngữ văn 9 có đáp án
- Trắc nghiệm Hóa học lớp 9 có đáp án
- Trắc nghiệm Địa lí lớp 9 có đáp án
- Trắc nghiệm Tiếng Anh lớp 9 có đáp án
- Trắc nghiệm GDCD lớp 9 có đáp án
- Trắc nghiệm Lịch sử lớp 9 có đáp án
- Trắc nghiệm Vật lí lớp 9 có đáp án
- Trắc nghiệm Công nghệ lớp 9 có đáp án
- Trắc nghiệm Sinh học lớp 10 có đáp án
- Trắc nghiệm Toán lớp 10 có đáp án
- Trắc nghiệm Hóa học lớp 10 có đáp án
- Trắc nghiệm Ngữ văn lớp 10 có đáp án
- Trắc nghiệm Vật Lí lớp 10 có đáp án
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án
- Trắc nghiệm Sinh học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Toán lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Hóa học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn lớp 11 có đáp án
- Trắc nghiệm Tiếng Anh lớp 11 có đáp án
- Trắc nghiệm Vật Lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Địa lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm GDCD lớp 11 có đáp án
- Trắc nghiệm Lịch sử lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Công nghệ lớp 11 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 11 có đáp án
- Trắc nghiệm Tin học lớp 11 có đáp án