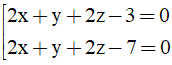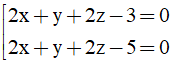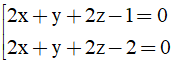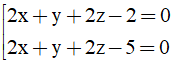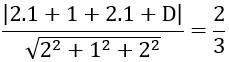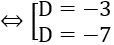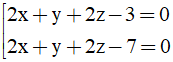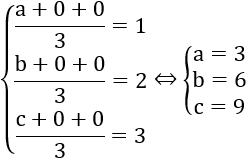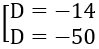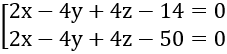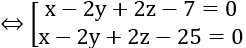TOP 40 câu Trắc nghiệm Phương trình mặt phẳng (có đáp án 2024) - Toán 12

Trắc nghiệm Toán 12 Bài 2: Phương trình mặt phẳng

Bài giảng Trắc nghiệm Toán 12 Bài 2: Phương trình mặt phẳng

Câu 1: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng $\left(\alpha \right)$ cắt các trục tọa độ tại A, B, C. Biết rằng trọng tâm của tam giác ABC là $G\left(-1;-3;2\right)$. Mặt phẳng $\left(\alpha \right)$ song song với mặt phẳng nào sau đây?

A. $6x+2y-3z-1=0.$

B. $6x+2y-3z+18=0.$

C. $6x+2y+3z-18=0.$

D. $6x-2y+3z-1=0.$

Hiển thị đáp án

Đáp án: B

Giải thích:

Giả sử $A(a;0;0),B(0;b;0),C(0;0;c)$

$\Rightarrow G(\frac{a}{3};\frac{b}{3};\frac{c}{3})$

$\Rightarrow a=-3,b=-9,c=6$

Do đó $\left(ABC\right):\frac{x}{-3}+\frac{y}{-9}+\frac{z}{6}=1$ hay $\left(ABC\right):6x+2y-3z+18=0$.

Câu 2: Trong không gian với hệ tọa độ Oxyz, cho các điểm $M\left(1;2;-3\right),N\left(-1;0;0\right),P\left(0;4;-3\right).$ Tính thể tích phần không gian giới hạn bởi mặt phẳng và các mặt phẳng tọa độ

A. $V=\frac{1}{3}$(đvtt).

B. $V=1$(đvtt).

C. $V=2$(đvtt).

D. $V=\frac{2}{3}$(đvtt).

Hiển thị đáp án

Đáp án: A

Giải thích:

$\overrightarrow{OM}=(1;2;-3),$

$\overrightarrow{ON}=(-1;0;0),$

$\overrightarrow{OP}=(0;4;-3)$

$\Rightarrow V_{OMNP}=\frac{1}{6}[\overrightarrow{OM},\overrightarrow{ON}].\overrightarrow{OP}=\frac{1}{3}$

Câu 3: Trong không gian với hệ tọa độ Oxyz, phương trình nào dưới đây là phương trình của mặt phẳng đi qua hai điểm $A\left(1;0;1\right),B\left(5;2;3\right)$ và vuông góc với mặt phẳng $\left(P\right):2x-y+z-7=0$?

A. $x+2z-3=0.$

B. $2x-y+z-3=0.$

C. $2x-y+z-11=0.$

D. $x-2z+1=0.$

Hiển thị đáp án

Đáp án: D

Giải thích:

$\overrightarrow{AB}=(4;2;2)$

$\Rightarrow \overrightarrow{n_{\alpha }}=[\overrightarrow{AB},\overrightarrow{n_P}]=(4;0;-8)$

$\Rightarrow \left(\alpha \right):x-2z+1=0$

Câu 4: Trong không gian với hệ tọa độ Oxyz, cho điểm $M\left(1;2;3\right).$ Gọi A, B và C lần lượt là hình chiếu vuông góc của M lên các trục tọa độ Ox, Oy và Oz. Viết phương trình mặt phẳng $\left(\alpha \right)$ đi qua ba điểm A, B và C.

A. $\left(\alpha \right):6x-3y+2z=0.$

B. $\left(\alpha \right):6x+3y+2z-6=0.$

C. $\left(\alpha \right):6x+3y+2z-18=0.$

D. $\left(\alpha \right):6x-3y+2z-6=0.$

Hiển thị đáp án

Đáp án: B

Giải thích:

$A(1;0;0),B(0;2;0),C(0;0;3)$

$\Rightarrow \left(ABC\right):\frac{x}{1}=\frac{y}{2}=\frac{z}{3}=1$

hay $6x+3y+2z-6=0$.

Câu 5: Trong không gian với hệ tọa độ Oxyz, cho $A\left(0;0;a\right),B\left(b;0;0\right),C\left(0;c;0\right),$ $a,b,c\in ℝ$ với và $abc\ne 0$. Viết phương trình mặt phẳng (ABC)

A. $\frac{x}{b}+\frac{y}{c}+\frac{z}{a}=1.$

B. $\frac{x}{c}+\frac{y}{b}+\frac{z}{a}=1.$

C. $\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1.$

D. $\frac{x}{b}+\frac{y}{a}+\frac{z}{c}=1.$

Hiển thị đáp án

Đáp án: A

Giải thích:

$\left(ABC\right):\frac{x}{b}=\frac{y}{c}=\frac{z}{a}=1$

Câu 6: Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng đi qua điểm và vuông góc với hai mặt phẳng $\left(P\right):x+y-z=2,$$\hspace{0.17em}\left(Q\right):x-y+z=1$

A. $\left(R\right):y+z-2=0.$

B. $\left(R\right):x+y+z-3=0.$

C. $\left(R\right):x+z-2=0.$

D. $\left(R\right):-x+2y-z=0.$

Hiển thị đáp án

Đáp án: A

Giải thích:

$\overrightarrow{n_R}=\left[\overrightarrow{n_P},\overrightarrow{n_Q}\right]=(0;-2;-2)$

$\Rightarrow \left(R\right):y+z-2=0$

Câu 7: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C và nhận điểm $G\left(1;2;1\right)$ là trọng tâm có phương trình là

A. $x+2y+2z-6=0.$

B. $2x+y+2z-6=0.$

C. $2x+2y+z-6=0.$

D. $2x+2y+6z-6=0.$

Hiển thị đáp án

Đáp án: B

Giải thích:

Giả sử $A(a;0;0),B(0;b;0),C(0;0;c)$

$\Rightarrow G(\frac{a}{3};\frac{b}{3};\frac{c}{3})$

$\Rightarrow a=3,b=6,c=3$

Ta có $\left(P\right):\frac{x}{3}+\frac{y}{6}+\frac{z}{3}=1$ hay $\left(P\right):2x+y+2z-6=0$.

Câu 8: Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng $\left(Q\right):x-y+3z-18=0$ và điểm $M\left(1;2;-3\right)$. Viết phương trình mặt phẳng (P) đi qua M và song song với (Q)

A. $\left(P\right):-x+y-3z+10=0.$

B. $\left(P\right):-x-y+3z-10=0.$

C. $\left(P\right):x-y+3z+10=0.$

D. $\left(P\right):-x+y+3z+10=0.$

Hiển thị đáp án

Đáp án: C

Giải thích:

$\overrightarrow{n_P}=\overrightarrow{n_Q}=(1;-1;3)$

$\Rightarrow \left(P\right):x-y+3z+10=0$

Câu 9: Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm $A\left(4;1;-2\right)$ và $B\left(6;9;2\right)$. Viết phương trình mặt phẳng trung trực của đoạn thẳng AB.

A. $x-4y+2z+25=0.$

B. $x-4y+2z-25=0.$

C. $x+4y+2z-25=0.$

D. $x-4y-2z-25=0.$

Hiển thị đáp án

Đáp án: C

Giải thích:

Gọi I là trung điểm của AB $\Rightarrow I(5;5;0)$

Ta có $\overrightarrow{n_P}=\overrightarrow{AB}=(2;8;4)$

Mà (P) qua $I\left(5;5;0\right)$ nên $\left(P\right):x+4y+2z-25=0$.

Câu 10: Trong không gian với hệ tọa độ Oxyz, cho hai điểm $A\left(1;1;5\right)$ và $B\left(0;-2;3\right)$. Viết phương trình mặt phẳng đi qua A, B và song song với trục Oy.

A. $2x+z+3=0.$

B. $2x-z+3=0.$

C. $-2x-z+3=0.$

D. $4x-4y-z+5=0.$

Hiển thị đáp án

Đáp án: B

Giải thích:

$\overrightarrow{AB}=(-1;-3;-2)$

$\Rightarrow \overrightarrow{n_P}=[\overrightarrow{AB},\overrightarrow{u_{Oy}}]=(2;0;-1)$

$\Rightarrow \left(P\right):2x-z+3=0$

Câu 11: Trong không gian với hệ tọa độ Oxyz, cho các điểm $A\left(2;-1;5\right)$, $B\left(1;2;-3\right)$, $C\left(1;0;2\right)$. Giả sử mặt phẳng (ABC) có phương trình là $x+ay+bz+c=0$. Hỏi các giá trị của a, b, c bằng bao nhiêu?

A. $a=-5,b=2,c=-3.$

B. $a=-5,b=-2,c=3.$

C. $a=5,b=-2,c=3.$

D. $a=5,b=2,c=-3.$

Hiển thị đáp án

Đáp án: B

Giải thích:

$\overrightarrow{AB}=(-1;3;-8),\overrightarrow{AC}=(-1;1;-3)$

$\Rightarrow \overrightarrow{n_P}=[\overrightarrow{AB},\overrightarrow{AC}]=(-1;5;2)$

$\Rightarrow \left(P\right):x-5y-2z+3=0$

Do đó suy ra $a=-5,b=-2,c=3$.

Câu 12: Trong không gian với hệ tọa độ Oxyz, phương trình nào dưới đây là phương trình đi qua điểm $M\left(1;2;-3\right)$ và trong vectơ pháp tuyến $\overrightarrow{n}=\left(1;-2;3\right)$?

A. $x-2y+3z-12=0.$

B. $x-2y-3z+6=0.$

C. $x-2y+3z+12=0.$

D. $x-2y-3z-6=0.$

Hiển thị đáp án

Đáp án: C

Giải thích:

$\left(P\right):1.(x-1)-2.(y-2)+3.(z+3)=0$

hay $\left(P\right):x-2y+3z+12=0$.

Câu 13: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng $\left(P\right):2x+7y-3z+2016=0$. Vectơ nào sau đây là vectơ pháp tuyến của mặt phẳng ?

A. $\overrightarrow{n}=\left(2;7;-3\right).$

B. $\overrightarrow{n}=\left(-2;-7;-3\right).$

C. $\overrightarrow{n}=\left(2;7;3\right).$

D. $\overrightarrow{n}=\left(-2;7;3\right).$

Hiển thị đáp án

Đáp án: A

Giải thích:

Vectơ pháp tuyến của mặt phẳng $\overrightarrow{n}=(2;7;-3)$.

Câu 14: Trong không gian với hệ tọa độ Oxyz, tọa độ vectơ pháp tuyến $\overrightarrow{n}$ của mặt phẳng $\left(\alpha \right):2x-5y-z+1=0$ là

A. $\overrightarrow{n}=\left(2;5;-1\right).$

B. $\overrightarrow{n}=\left(2;5;1\right).$

C. $\overrightarrow{n}=\left(-2;5;-1\right).$

D. $\overrightarrow{n}=\left(-4;10;2\right).$

Hiển thị đáp án

Đáp án: D

Giải thích:

Vectơ pháp tuyến của mặt phẳng $\overrightarrow{n}=(-4;10;2)$.

Câu 15: Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng $\left(P\right):x-y+3=0$. Vectơ nào không phải là vecto pháp tuyến của mặt phẳng (P)?

A. $\overrightarrow{a_1}=\left(3;-3;0\right).$

B. $\overrightarrow{a_2}=\left(1;-1;3\right).$

C. $\overrightarrow{a_3}=\left(-1;1;0\right).$

D. $\overrightarrow{a_4}=\left(1;-1;0\right).$

Hiển thị đáp án

Đáp án: B

Giải thích:

Vectơ $\overrightarrow{a_2}=(1;-1;3)$ không phải là vectơ pháp tuyến của mặt phẳng.

Câu 16: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng $\left(P\right):\frac{x}{3}+\frac{y}{2}+\frac{z}{1}=1$. Vectơ nào sau đây là vectơ pháp tuyến của mặt phẳng ?

A. $\overrightarrow{n}=\left(2;3;6\right).$

B. $\overrightarrow{n}=\left(3;2;1\right).$

C. $\overrightarrow{n}=\left(6;3;2\right).$

D. $\overrightarrow{n}=\left(1;\frac{1}{2};\frac{1}{3}\right).$

Hiển thị đáp án

Đáp án: A

Giải thích:

$\left(P\right):2x+3y+6z-6=0$ nên có vectơ pháp tuyến $\overrightarrow{n}=(2;3;6)$.

Câu 17: Trong không gian với hệ tọa độ Oxyz, cho điểm $M\left(3;-1;-2\right)$ và mặt phẳng

$\left(\alpha \right):3x-y+2z+4=0$. Phương trình nào dưới đây là phương trình mặt phẳng đi qua M và song song với $\left(\alpha \right)$.

A. $3x+y-2z-14=0.$

B. $3x-y+2z+6=0.$

C. $3x-y+2z-6=0.$

D. $3x-y-2z+6=0.$

Hiển thị đáp án

Đáp án: C

Giải thích:

Phương trình m dạng $\left(\beta \right):3x-y+2z+m=0$ mà (β) qua $M(3;-1;-2)\Rightarrow m=-6$

Do đó phương trình mặt phẳng là $\left(\beta \right):3x-y+2z-6=0$.

Câu 18: Trong không gian với hệ tọa độ Oxyz, phương trình mặt phẳng (P) đi qua hai điểm $A\left(0;1;0\right)$, $B\left(2;3;1\right)$ và vuông góc với mặt phẳng $\left(Q\right):x+2y-z=0.$

A. $4x+3y-2z-3=0.$

B. $4x-3y-2z+3=0.$

C. $x-2y-3z-11=0.$

D. $x+2y-3z+7=0.$

Hiển thị đáp án

Đáp án: B

Giải thích:

$\overrightarrow{AB}=(2;2;1)$

$\Rightarrow \overrightarrow{n_P}=[\overrightarrow{AB},\overrightarrow{n_Q}]=(-4;3;2)$

$\Rightarrow \left(P\right):4x-3y-2z+3=0$

Câu 19: Trong không gian với hệ tọa độ Oxyz, cho hai điểm $A\left(1;-1;5\right)$ và $B\left(0;0;1\right)$. Viết phương trình mặt phẳng (P) chứa A, B và song song với trục Oy.

A. $4x+y-z+1=0.$

B. $2x+z-5=0.$

C. $4x-z+1=0.$

D. $y+4z-1=0.$

Hiển thị đáp án

Đáp án: C

Giải thích:

$\overrightarrow{AB}=(-1;1;-4)$

$\Rightarrow \overrightarrow{n_P}=[\overrightarrow{AB},\overrightarrow{u_{Oy}}]=(4;0;-1)$

$\Rightarrow \left(P\right):4x-z+1=0$

Câu 20: Trong không gian với hệ tọa độ Oxyz, cho điểm $A\left(3;-1;2\right)$ và mặt phẳng (P) có phương trình $2x-y+4z+2017=0$. Lập phương trình mặt phẳng $\left(\alpha \right)$ đi qua A và song song với (P)

A. $2x-y+4z-15=0.$

B. $2x-y+4z-13=0.$

C. $3x-y+2z-15=0.$

D. $3x-y+2z-2017=0.$

Hiển thị đáp án

Đáp án: A

Giải thích:

$\overrightarrow{n_{\alpha }}=\overrightarrow{n_P}=(2;-1;4)$

$\to \left(\alpha \right):2x-y+4z-15=0$

Câu 21: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng $\left(P\right):2x-2y+z+3=0$ và đường thẳng $d:\frac{x-2}{2}=\frac{y-3}{-1}=\frac{z-3}{2}$. Mặt phẳng (Q) chứa d và vuông góc với (P) có phương trình là

A. $3x+2y+2z-6=0.$

B. $3x+2y-2z+6=0.$

C. $3x-2y-2z+6=0.$

D. $3x+2y-2z-6=0.$

Hiển thị đáp án

Đáp án: D

Giải thích:

$\overrightarrow{n_Q}=\left[\overrightarrow{n_P},\overrightarrow{u_d}\right]=(-3;-2;2)$

$\Rightarrow \left(Q\right):3x+2y-2z-6=0$

Câu 22: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng $\left(P\right):x-2y+z-5=0$. Điểm nào dưới đây thuộc (P)?

A. $Q\left(2;-1;5\right).$

B. $P\left(0;0;-5\right).$

C. $N\left(-5;0;0\right).$

D. $M\left(1;1;6\right).$

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có $1-2.1+6-5=0$

$\Rightarrow M(1;1;6)\in \left(P\right)$.

Câu 23: Trong không gian với hệ tọa độ Oxyz, phương trình nào dưới đây là phương trình mặt phẳng đi qua điểm $M\left(3;-1;1\right)$ và vuông góc với đường thẳng $\Delta :\frac{x-1}{3}=\frac{y+2}{-2}=\frac{z-3}{1}$?

A. $3x-2y+z+12=0.$

B. $3x+2y+z-8=0.$

C. $3x-2y+z-12=0.$

D. $x-2y+3z+3=0.$

Hiển thị đáp án

Đáp án: C

Giải thích:

$\overrightarrow{n_P}=\overrightarrow{n_{\Delta }}=(3;-2;1)$

$\to \left(P\right):3x-2y+z-12=0$

Câu 24: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng $\left(\alpha \right):x+y+z-6=0$. Điểm nào dưới đây là không thuộc $\left(\alpha \right)$?

A. $N\left(2;2;2\right).$

B. $Q\left(3;3;0\right).$

C. $P\left(1;2;3\right).$

D. $M\left(1;-1;1\right).$

Hiển thị đáp án

Đáp án: D

Giải thích:

$M(1;-1;1)\notin \left(P\right)$.

Câu 25: Trong không gian với hệ tọa độ Oxyz, cho hai điểm $A\left(1;0;-2\right)$, $B\left(0;-4;-4\right)$ và mặt phẳng $\left(P\right):3x-2y+6z+2=0$. Phương trình mặt phẳng (Q) chứa đường thẳng AB và vuông góc với mặt phẳng (P) là

A. $2x-z-4=0.$

B. $2x+y-z-4=0.$

C. $2x-y-z-4=0.$

D. $4x+y-4z-12=0.$

Hiển thị đáp án

Đáp án: A

Giải thích:

$\overrightarrow{AB}=(-1;-4;-2)$

$\Rightarrow \overrightarrow{n_Q}=[\overrightarrow{AB},\overrightarrow{n_P}]=(-28;0;14)$

$\Rightarrow \left(Q\right):2x-z-4=0$

Câu 26: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C và nhận điểm G(1;2;1) là trọng tâm có phương trình là

A. $x+2y+2z-6=0.$

B. $2x+y+2z-6=0.$

C. $2x+2y+z-6=0.$

D. $2x+2y+6z-6=0.$

Hiển thị đáp án

Đáp án: B

Giải thích:

Giả sử $A(a;0;0),B(0;b;0),C(0;0;c)$

$\Rightarrow G(\frac{a}{3};\frac{b}{3};\frac{c}{3})$

$\Rightarrow a=3,b=6,c=3$

Ta có $\left(P\right):\frac{x}{3}+\frac{y}{6}+\frac{z}{3}=1$ hay $\left(P\right):2x+y+2z-6=0$.

Câu 27: Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng $\left(Q\right):x-y+3z-18=0$ và điểm $M\left(1;2;-3\right)$. Viết phương trình mặt phẳng (P) đi qua M và song song với (Q)

A. $\left(P\right):-x+y-3z+10=0.$

B. $\left(P\right):-x-y+3z-10=0.$

C. $\left(P\right):x-y+3z+10=0.$

D. $\left(P\right):-x+y+3z+10=0.$

Hiển thị đáp án

Đáp án: C

Giải thích:

$\overrightarrow{n_P}=\overrightarrow{n_Q}=(1;-1;3)$

$\Rightarrow \left(P\right):x-y+3z+10=0$

Câu 28: Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;1;5) và B(0;-2;3). Viết phương trình mặt phẳng đi qua A, B và song song với trục Oy.

A. $2x+z+3=0.$

B. $2x-z+3=0.$

C. $-2x-z+3=0.$

D. $4x-4y-z+5=0.$

Hiển thị đáp án

Đáp án: B

Giải thích:

$\overrightarrow{AB}=(-1;-3;-2)$

$\Rightarrow \overrightarrow{n_P}=[\overrightarrow{AB},\overrightarrow{u_{Oy}}]=(2;0;-1)$

$\Rightarrow \left(P\right):2x-z+3=0$

Câu 29: Trong không gian với hệ tọa độ Oxyz, cho các điểm $A\left(2;-1;5\right)$, $B\left(1;2;-3\right)$, $C\left(1;0;2\right)$. Giả sử mặt phẳng (ABC) có phương trình là $x+ay+bz+c=0$. Hỏi các giá trị của a, b, c bằng bao nhiêu?

A. $a=-5,b=2,c=-3.$

B. $a=-5,b=-2,c=3.$

C. $a=5,b=-2,c=3.$

D. $a=5,b=2,c=-3.$

Hiển thị đáp án

Đáp án: B

Giải thích:

$\overrightarrow{AB}=(-1;3;-8),\overrightarrow{AC}=(-1;1;-3)$

$\Rightarrow \overrightarrow{n_P}=[\overrightarrow{AB},\overrightarrow{AC}]=(-1;5;2)$

$\Rightarrow \left(P\right):x-5y-2z+3=0$

Do đó suy ra $a=-5,b=-2,c=3$.

Câu 30: Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm $P\left(0;8;-2\right)$, $Q\left(1;0;2\right)$ và mặt phẳng $\left(\beta \right):-x+5y+2z-3=0$. Viết phương trình mặt phẳng $\left(\alpha \right)$ đi qua P, Q và vuông góc với mặt phẳng $\left(\beta \right).$

A. $\left(\alpha \right):-20x+y+7z+6=0.$

B. $\left(\alpha \right):12x+2y+z-14=0.$

C. $\left(\alpha \right):12x+2y-z-14=0.$

D. $\left(\alpha \right):$$y+2z-4=0.$

Hiển thị đáp án

Đáp án: B

Giải thích:

$\overrightarrow{PQ}=(1;-8;4)$

$\Rightarrow \overrightarrow{n_{\alpha }}=[\overrightarrow{PQ},\overrightarrow{n_{\beta }}]=(-36;-6;-3)$

$\Rightarrow \left(\alpha \right):12x+2y+z-14=0$

Câu 31: Trong không gian Oxyz, Phương trình mặt phẳng (P) chứa trục Ox và vuông góc với mặt phẳng (Q): 3x + y - 2z - 5 = 0 là

A. -x +3y =0

B. 2x +3y =0

C. 2y -z =0

D. 2y +z =0

Hiển thị đáp án

Đáp án: D

Giải thích:

Trục Ox có vecto chỉ phương u→=(1;0;0) và đi qua điểm O (0; 0; 0)

Mặt phẳng (Q) có vecto pháp tuyến nQ→=(3;1; -2)

Do mặt phẳng (P) chứa trục Ox và vuông góc với mặt phẳng (Q) nên mặt phẳng (P) có vecto pháp tuyến là n→=[u→ ; nQ→ ]=(0;2;1)

Phương trình mặt phẳng (P) có vecto pháp tuyến n→ và đi qua điểm O là:

2y +z =0

Câu 32: Trong không gian Oxyz, cho điểm A(1;1;1) và mặt phẳng (Q): 2x + y + 2z - 1 = 0. Mặt phẳng (P) song song với mặt phẳng (Q) và khoảng cách từ A đến mặt phẳng (P) bằng 2/3. Phương trình mặt phẳng (P) là

A.

B.

C.

D.

Hiển thị đáp án

Đáp án: A

Giải thích:

Mặt phẳng (P) song song với mặt phẳng (Q) nên phương trình mặt phẳng (P) có dạng:

2x +y +2z +D =0 (D≠ -1)

Khoảng cách từ A đến mặt phẳng (P) bằng 2/3 nên ta có:

⇔ |5 +D| =2

Vậy phương trình mặt phẳng (P) cần tìm là:

Câu 33: Trong không gian Oxyz phương trình mặt phẳng (P) đi qua điểm A(2; -1; 2) song song trục Oy và vuông góc với mặt phẳng (Q): 2x - y + 3z - 9 = 0 là

A. 3y + z + 1 = 0

B. x + 2y = 0

C. 3x - 2z - 2 = 0

D. 3x + 2y - 10 = 0

Hiển thị đáp án

Đáp án: C

Giải thích:

Trục Oy có vecto chỉ phương là u→=(0;1;0)

Mặt phẳng (Q) có vecto pháp tuyến nQ→=(2;-1;3)

Do mặt phẳng (P) chứa trục Ox và vuông góc với mặt phẳng (Q) nên mặt phẳng (P) có vecto pháp tuyến là n→=[u→ ; nQ→ ]=(3;0; -2)

Phương trình mặt phẳng (P) có vecto pháp tuyến n→ và đi qua điểm A(2; -1; 2) là:

3(x -2) -2(z -2) =0

⇔ 3x -2z -2 =0

Câu 34: Phương trình mặt phẳng (α) đi qua M(1; -2; 3) và song song với mặt phẳng (β): 2x – 3y + z + 5 = 0 là :

A. 2x – 3y +z -11 = 0

B. –x – 2y +3z -11 = 0

C. 2x – 3y +2z +11 = 0

D. 2x – 3y +z +11 = 0

Hiển thị đáp án

Đáp án: A

Giải thích:

Mặt phẳng (α) song song với mặt phẳng (β): 2x – 3y + z + 5 = 0 nên phương trình mặt phẳng (α) có dạng: 2x -3y +z +D =0 (D≠5)

Mặt phẳng (α) đi qua M(1; -2; 3) nên:

2 .1 -3 .(-2) +3 +D =0 ⇒ D= -11

Vậy phương trình mặt phẳng cần tìm là 2x -3y +z -11 =0

Câu 35: Phương trình mặt phẳng (α) đi qua hai điểm A(3;1;-1), B(2;-1;4) và vuông góc với mặt phẳng có phương trình (β): 2x - y + 3z = 0 là :

A. 2x - y+3z -2 = 0

B. x -13y - 5z + 5 = 0

C. - x +13y + 5z = 0

D. x -13y - 5z +6 = 0

Hiển thị đáp án

Đáp án: B

Giải thích:

AB→ =(-1; -2;5)

Mặt phẳng (β) có vecto pháp tuyến n1→=(2 ; -1 ;3)

Do mặt phẳng (α) đi qua hai điểm A, B và vuông góc với mặt phẳng (β) nên có vecto pháp tuyến là n→=[AB→ ; n1→ ]=(-1;13;5)

Phương trình mặt phẳng (α) có vecto pháp tuyến n→ và đi qua điểm A(3 ; 1 ; -1) là :

-(x -3) +13(y -1) +5(z +1) =0

⇔ x -13y -5z +5 =0

Câu 36: Trong không gian với hệ toạ độ Oxyz, (α) là mặt phẳng đi qua điểm A(2; -1; 5) và vuông góc với hai mặt phẳng (P): 3x - 2y + z + 7 = 0 và (Q): 5x - 4y + 3z + 1 = 0. Phương trình mặt phẳng (α) là:

A. x + 2y + z - 5 = 0

B. 2x - 4y - 2z - 10 = 0

C. 2x + 4y + 2z + 10 = 0

D. x + 2y - z + 5 = 0

Hiển thị đáp án

Đáp án: A

Giải thích:

Mặt phẳng (P) có vecto pháp tuyến n1→=(3; -2;1)

Mặt phẳng (Q) có vecto pháp tuyến n2→=(5; -4;3)

Do mặt phẳng (α) vuông góc với 2 mặt phẳng (P) và (Q) nên vecto pháp tuyến của mặt phẳng (α) là n→=[n1→ , n2→ ]=(-2; -4; -2)= -2(1;2;1)

Phương trình mặt phẳng (α) đi qua A (2; -1; 5) và có vecto pháp tuyến n→=(1;2;1) là: x -2 +2(y +1) +z -5 =0

⇔ x +2y +z -5 =0

Câu 37: Trong không gian với hệ toạ độ Oxyz, gọi (α) là mặt phẳng qua G(1;2;3) và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác gốc O) sao cho G là trọng tâm của tam giác ABC. Khi đó mặt phẳng (α) có phương trình:

A. 6x + 3y + 2z - 18 = 0

B. 3x + 6y + 2z + 18 = 0

C. 2x + y + 3z - 9 = 0

D. 6x + 3y + 2z + 9 = 0

Hiển thị đáp án

Đáp án: A

Giải thích:

Giả sử tọa độ của các điểm là A (a; 0; 0), B (0; b; 0), C (0; 0; c)

Do G(1; 2; 3) là trọng tâm tam giác ABC nên ta có:

Mặt phẳng (α) đi qua A (3; 0; 0), B (0; 6; 0), C (0; 0; 9) có phương trình là:

x/3 +y/6 +z/9 =1

⇔ 6x +3y +2z -18 =0

Câu 38: Trong không gian với hệ toạ độ Oxyz, gọi (α) là mặt phẳng song song với mặt phẳng (β): 2x - 4y + 4z + 3 = 0 và cách điểm A(2; -3; 4) một khoảng k=3. Phương trình của mặt phẳng (α) là:

A. x - 2y + 2z - 25 = 0 hoặc x - 2y + 2z - 7 = 0

B. x - 2y + 2z - 25 = 0

C. x - 2y + 2z - 7 = 0

D. 2x - 4y + 4z - 5 = 0 hoặc 2x - 4y + 4z - 13 = 0

Hiển thị đáp án

Đáp án: A

Giải thích:

Phương trình mặt phẳng song song với mặt phẳng là:

2x -4y +4z +D =0 (D≠ 3)

Do cách điểm A( 2; -3; 4) một khoảng k = 3 nên ta có:

=3

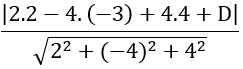
⇔ |32 +D| =18 ⇔

Vậy phương trình mặt phẳng là:

Câu 39: Trong không gian với hệ toạ độ Oxyz, cho A(1;0;0), B(0; b; 0), C(0; 0; c) (b > 0, c > 0) và mặt phẳng (P): y - z + 1 = 0. Viết phương trình mặt phẳng (ABC) biết mặt phẳng (ABC) vuông góc với mặt phẳng (P) và khoảng cách từ O đến (ABC) bằng 1/3 .

A. x + 2y + z - 12 = 0

B. x + 2y + 2z - 1 = 0

C. 5x + 4y + 3z - 50 = 0

D. x - y + z = 0

Hiển thị đáp án

Đáp án: B

Giải thích:

Phương trình mặt phẳng (ABC) đi qua A(1;0;0), B(0; b; 0), C(0; 0; c) (b > 0, c > 0) là:

x/1 +y/b +z/c =1 ⇔ bcx +cy +bz -bc =0

Mặt phẳng (ABC) có vecto pháp tuyến n→=(bc; c; b)

Mặt phẳng (P) có vecto pháp tuyến n1→=(0;1; -1)

Do mặt phẳng (ABC) vuông góc với mặt phẳng (P) nên n→ .n1→=0

⇔ c -b =0 ⇔ b =c

Khi đó phương trình mặt phẳng (ABC) là: b2 x +by +bz -b2 =0

⇔ bx +y +z -b =0

Khoảng cách từ O đến (ABC) bằng nên:

=1/3 ⇔ 9b2 =b2 +2 ⇔ b = 1/2 (do b > 0)

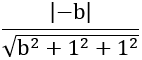
Vậy phương trình mặt phẳng (ABC) là

1/2 x +y +z -1/2 =0 ⇔ x +2y +2z -1 =0

Câu 40: Trong không gian với hệ toạ độ Oxyz, mặt phẳng (α) đi qua điểm M(5;4;3) và cắt các tia Ox, Oy, Oz các đoạn bằng nhau có phương trình là:

A. x + y + z - 12 = 0

B. x + y + z = 0

C. 5x + 4y + 3z - 50 = 0

D. x - y + z = 0

Hiển thị đáp án

Đáp án: A

Giải thích:

Do mặt phẳng (α) cắt các tia Ox, Oy, Oz các đoạn bằng nhau nên mặt phẳng (α) có phương trình:

x/a +y/a +z/a =1

Mặt khác, mặt phẳng (α) đi qua M (5; 4; 3) nên ta có:

5/a +4/a +3/a =1 ⇔ a=12

Vậy phương trình mặt phẳng (α) là:

x/12 +y/12 +z/12 =1 ⇔ x +y +z -12 =0

Các câu hỏi trắc nghiệm Toán lớp 12 có đáp án, chọn lọc khác:

Trắc nghiệm Mặt cầu có đáp án

Trắc nghiệm Ôn tập Chương 2 - Mặt nón. Mặt trụ. Mặt cầu có đáp án

Trắc nghiệm Hệ tọa độ trong không gian có đáp án

Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án

Trắc nghiệm Ôn tập Chương 3 - Phương pháp tọa độ trong không gian có đáp án