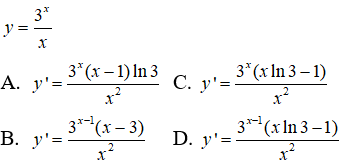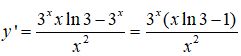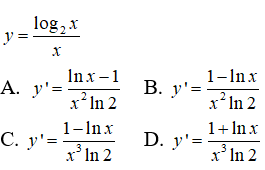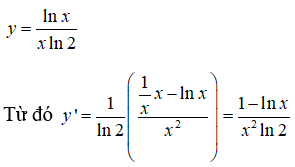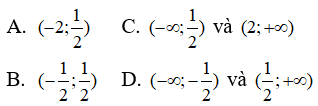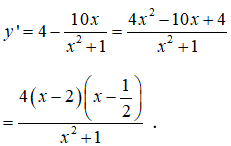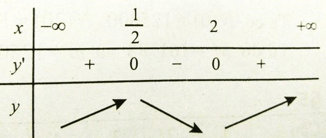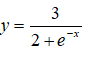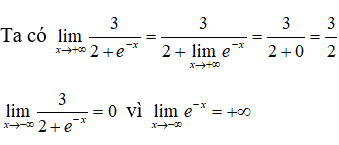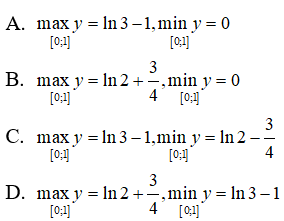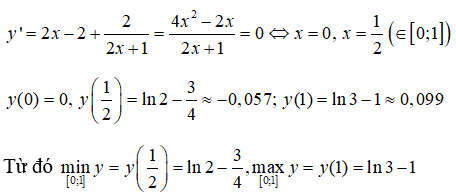TOP 40 câu Trắc nghiệm Hàm số mũ. Hàm số Logarit (có đáp án 2024) - Toán 12

Trắc nghiệm Toán 12 Bài 4: Hàm số mũ. Hàm số Logarit

Bài giảng Trắc nghiệm Toán 12 Bài 4: Hàm số mũ. Hàm số Logarit

Câu 1. Tìm mệnh đề đúng trong các mệnh đề sau:

A. Đồ thị hàm số $y=a^x$ và đồ thị hàm số $y={\log }_{a}x$ đối xứng nhau qua đường thẳng y = x.

B. Hàm số $y=a^x$ với $0<a<1$ đồng biến trên khoảng $(-\infty ;+\infty )$.

C. Hàm số $y=a^x$ với $a>1$ nghịch biến trên khoảng $(-\infty ;+\infty )$.

D. Đồ thị hàm số $y=a^x$ với $a>0$ và $a\ne 1$ luôn đi qua điểm $M(a;1)$.

Hiển thị đáp án

Đáp án: A

Giải thích:

Câu B sai vì hàm số $y=a^x$ với $0<a<1$ nghịch biến trên khoảng $(-\infty ;+\infty )$.

Câu C sai vì hàm số $y=a^x$ với $a>1$ đồng biến trên khoảng $(-\infty ;+\infty )$.

Câu D sai vì đồ thị hàm số $y=a^x$ với $a>0$ và $a\ne 1$ luôn đi qua điểm $M(a;a^a)$ hoặc $M(0;1)$ chứ không phải $M(a;1)$.

Câu 2. Tập giá trị của hàm số $y=a^x(a>0;a\ne 1)$ là:

A. $(0;+\infty )$

B. $\text{[}0;+\infty )$

C. $ℝ\backslash \text{{}0\}$

D. $ℝ$

Hiển thị đáp án

Đáp án: A

Giải thích:

Với $a>0;a\ne 1$ thì $a^x>0$, $\forall x\in ℝ$. Suy ra tập giá trị của hàm số $y=a^x(a>0;a\ne 1)$ là $(0;+\infty )$.

Câu 3. Với $a>0$ và $a\ne 1$. Phát biểu nào sau đây không đúng?

A. Hai hàm số $y=a^x$ và $y={\log }_{a}x$ có cùng tập giá trị.

B. Hai hàm số $y=a^x$ và $y={\log }_{a}x$ có cùng tính đơn điệu.

C. Đồ thị hai hàm số $y=a^x$ và $y={\log }_{a}x$ đối xứng nhau qua đường thẳng $y=x$.

D. Đồ thị hai hàm số $y=a^x$ và $y={\log }_{a}x$ đều có đường tiệm cận.

Hiển thị đáp án

Đáp án: A

Giải thích:

Tập giá trị của hàm số $y=a^x$ là $(0;+\infty )$, tập giá trị của hàm số $y={\log }_{a}x$ là $ℝ$.

Câu 4. Tìm x để hàm số $y=\log \sqrt{x^2+x-12}$ có nghĩa.

A. $x\in (-\infty ;-4)\cup (3;+\infty )$

B. $x\in (-4;3)$

C. $\left\{\begin{array}{l}x\ne -4\\ x\ne 3\end{array}\right.$

D. $x\in R$.

Hiển thị đáp án

Đáp án: A

Giải thích:

Hàm số $\log \sqrt{x^2+x-12}$ có nghĩa khi $x^2+x-12>0$ $\iff \left[\begin{array}{l}x>3\\ x<-4\end{array}\right.$

Câu 5. Tập xác định của hàm số $y={\log }_2\frac{x+3}{2-x}$ là:

A. $D=(-3;2)$

B. $D=ℝ\backslash \text{{}-\text{3};2\}$

C. $D=(-\infty ;-3)\cup (2;+\infty )$

D. $D=\text{[}-\text{3};2]$

Hiển thị đáp án

Đáp án: A

Giải thích:

Hàm số ${\log }_2\frac{x+3}{2-x}$ có nghĩa khi $\frac{x+3}{2-x}>0$

$\iff -3<x<2$

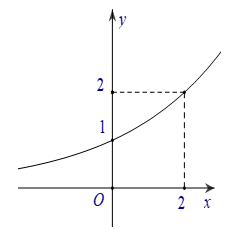
Câu 6. Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

A. $y={\left(\sqrt{2}\right)}^x$

B. $y=x$

C. $y=2^x$

D. $y={\left(\sqrt{2}\right)}^{-x}$

Hiển thị đáp án

Đáp án: A

Giải thích:

Nhận thấy đây là đồ thị hàm số dạng $y=a^x$. Ta có $A(0;1)$ và $B(2;2)$ thuộc đồ thị hàm số.

Suy ra, $\left\{\begin{array}{l}{a}^0=1\\ a^2=2\\ a>0\end{array}\right.\Rightarrow a=\sqrt{2}$ . Hàm số là $y={\left(\sqrt{2}\right)}^x$.

Câu 7. Đạo hàm của hàm số $y=\sin x+{\log }_3{x}^3(x>0)$ là:

A. $y\text{'}=\cos x+\frac{3}{x\ln 3}$

B. $y\text{'}=-\cos x+\frac{3}{x\ln 3}$

C. $y\text{'}=\cos x+\frac{1}{x^3\ln 3}$

D. $y\text{'}=-\cos x+\frac{1}{x^3\ln 3}$

Hiển thị đáp án

Đáp án: A

Giải thích:

$y=\sin x+{\log }_3{x}^3$

$\Rightarrow y\text{'}=\cos \text{x}+\frac{3{\text{x}}^2}{x^3\ln 3}$

$=\cos \text{x}+\frac{3}{x\ln 3}$

Câu 8. Cho hàm số $f\left(x\right)=\ln \left(x^4+1\right)$. Đạo hàm $f^{/}\left(0\right)$ bằng:

A. 1

B. 2

C. 3

D. 4

Hiển thị đáp án

Đáp án: A

Giải thích:

$f\left(x\right)=\ln (x^4+1)$

$\Rightarrow f\text{'}\left(x\right)=\frac{(x^4+1)\text{'}}{x^4+1}$

$=\frac{4{\text{x}}^3}{x^4+1}$

$\Rightarrow f\text{'}\left(0\right)=0$

Câu 9. Cho hàm số $f\left(x\right)=x{e}^x$. Gọi ${f^{/}}^{/}\left(x\right)$ là đạo hàm cấp hai của $f\left(x\right)$. Ta có ${f^{/}}^{/}\left(1\right)$ bằng:

A. $3e$

B. $-3e^2$

C. $e^3$

D. $-5e^2$

Hiển thị đáp án

Đáp án: A

Giải thích:

$f\left(x\right)=x.e^x$

$\Rightarrow f\text{'}\left(x\right)=e^x+x.e^x$

$\Rightarrow f\text{'}\text{'}\left(x\right)=e^x+e^x+x.e^x$

$\Rightarrow f\text{'}\text{'}\left(1\right)=3\text{e}$

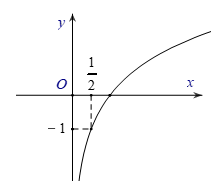
Câu 10. Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

A. $y={\log }_{2}x$

B. $y={\log }_{\frac{1}{2}}x$

C. $y={\log }_{\sqrt{2}}x$

D. $y={\log }_2\left(2x\right)$

Hiển thị đáp án

Đáp án: A

Giải thích:

Nhận thấy đây là đồ thị hàm số $y={\log }_{a}x$. Điểm $\left(\frac{1}{2};-1\right)$ thuộc đồ thị hàm số nên $-1={\log }_a\frac{1}{2}$ $\Rightarrow a^{-1}=\frac{1}{2}$ $\Rightarrow \frac{1}{a}=\frac{1}{2}\Rightarrow a=2$ .

Hàm số là $y={\log }_{2}x$.

Câu 11. Gọi (C) là đồ thị hàm số $y=\log x$. Tìm khẳng định đúng?

A. Đồ thị (C) có tiệm cận đứng.

B. Đồ thị (C) có tiệm cận ngang.

C. Đồ thị (C) cắt trục tung.

D. Đồ thị (C) không cắt trục hoành.

Hiển thị đáp án

Đáp án: A

Giải thích:

- Đồ thị hàm số $y=\log x$ nhận trục tung là tiệm cận đứng.

- Đồ thị hàm số không có tiệm cận ngang và cắt trục hoành tại điểm (1; 0) nên các đáp án B, C, D đều sai.

Câu 12. Cho hàm số $y=5^x$ có đồ thị (C). Hàm số nào sau đây có đồ thị đối xứng với (C) qua đường thẳng y = x.

A. $y=5^{-x}$

B. $y={\log }_{5}x$

C. $y=-5^{-x}$

D. $y=-{\log }_{5}x$

Hiển thị đáp án

Đáp án: B

Giải thích:

Đồ thị hàm số $y=5^x$ đối xứng với đồ thị hàm số $y={\log }_{5}x$ qua đường thẳng y = x.

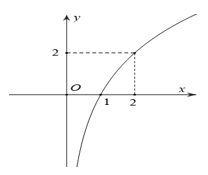
Câu 13. Tìm tất cả các giá trị thực của a để hàm số $y={\log }_{a}x$ $\left(0<a\ne 1\right)$ có đồ thị là hình bên ?

A. $a=\sqrt{2}$

B. $a=2$

C. $a=\frac{1}{2}$

D. $a=\frac{1}{\sqrt{2}}$

Hiển thị đáp án

Đáp án: A

Giải thích:

Nhận dạng đồ thị:

- Dựa vào đồ thị thì hàm đã cho đồng biến $\Rightarrow$ loại C và D.

- Đồ thị đã cho qua điểm $A\left(2;2\right)$. Thử với hai đáp án còn lại $\Rightarrow$ loại B.

Câu 14. Tìm giá trị lớn nhất của hàm số $f\left(x\right)=x^2{e}^x$ trên đoạn $\left[-1;1\right]$?

A. e

B. $\frac{1}{e}$

C. 2e

D. 0

Hiển thị đáp án

Đáp án: A

Giải thích:

Trên đoạn $\left[-1;1\right]$, ta có: $f^{/}\left(x\right)=x{e}^x\left(x+2\right)$; $f^{/}\left(x\right)=0\iff x=0$ hoặc $x=-2$ (loại).

Ta có: $f\left(-1\right)=\frac{1}{e};$

$f\left(0\right)=0;f\left(1\right)=e$

Suy ra: $\underset{\left[-1;1\right]}{\max }f\left(x\right)=e$

Câu 15. Cho ba số thực dương a, b, c khác 1. Đồ thị các hàm số $y={\log }_{a}x,y={\log }_{b}x,{\log }_{c}x$ được cho trong hình vẽ sau:

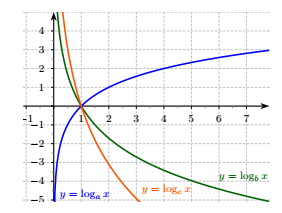
Mệnh đề nào dưới đây đúng?

A. $a<b<c$

B. $b<c<a$

C. $a<c<b$

D. $c<a<b$

Hiển thị đáp án

Đáp án: B

Giải thích:

Quan sát hình vẽ ta thấy:

- Hàm số $y={\log }_{a}x$ là hàm đồng biến nên ta có a > 1.

- Hai hàm số $y={\log }_{b}x,{\log }_{c}x$ nghịch biến nên có $0<b,c<1$

Từ nhận xét này ta thấy a là số lớn nhất.

Câu 16. Hàm số nào sau đây nghịch biến trên R.

A. $y={2017}^x$

B. $y={\log }_{\frac{1}{2}}x$

C. $y={\log }_{\sqrt{2}}\left(x^2+1\right)$

D. $y={\left(\frac{\pi }{4}\right)}^x$

Hiển thị đáp án

Đáp án: D

Giải thích:

Hàm số $y={2017}^x$ có TXĐ: D = R; cơ số 2017 > 1 nên đồng biến trên R

Hàm số $y={\log }_{\frac{1}{2}}x$ có TXĐ: $D=\left(0;+\infty \right)$ nên không thỏa mãn.

Hàm số $y={\log }_{\sqrt{2}}\left(x^2+1\right)$ có TXĐ: D = R

Ta có: $y\text{'}=\frac{2x}{\left(x^2+1\right)\ln \sqrt{2}}$ nên hàm số $y={\log }_{\sqrt{2}}\left(x^2+1\right)$ đồng biến khi x > 0, nghịch biến khi x < 0. Do đó C sai.

Hàm số $y={\left(\frac{\pi }{4}\right)}^x$ có TXĐ: D = R cơ số $\frac{\pi }{4}<1$ nên nghịch biến trên R

Câu 17. Cho hàm số $y={\log }_2\left(2x\right)$. Khi đó, hàm số $y=\left|{\log }_2\left(2x\right)\right|$ có đồ thị là hình nào trong bốn hình được liệt kê ở bốn phương án A, B, C, D dưới đây:

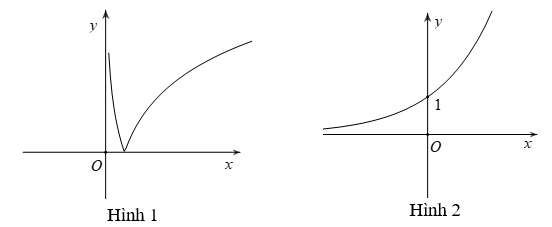
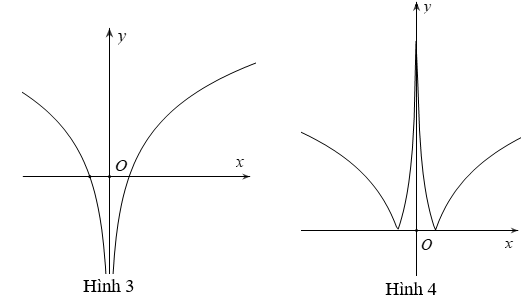
A. Hình 1

B. Hình 2

C. Hình 3

D. Hình 4

Hiển thị đáp án

Đáp án: A

Giải thích:

Sử dụng lý thuyết phép suy đồ thị.

Câu 18. Hình bên là đồ thị của ba hàm số $y={\log }_{a}x$, $y={\log }_{b}x$, $y={\log }_{c}x$ $\left(0<a,b,c\ne 1\right)$ được vẽ trên cùng một hệ trục tọa độ. Khẳng định nào sau đây là khẳng định đúng?

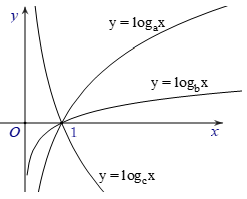
A. $b>a>c$

B. $a>b>c$

C. $b>c>a$

D. $a>c>b$

Hiển thị đáp án

Đáp án: A

Giải thích:

Do $y={\log }_{a}x$ và $y={\log }_{b}x$ là hai hàm dồng biến nên $a,b>1$

Do $y={\log }_{c}x$ nghịch biến nên $c<1$. Vậy bé nhất.

Mặt khác: Lấy $y=m$, khi đó tồn tại $x_1,x_2>0$ để $\left\{\begin{array}{l}{\log }_a{x}_1=m\\ {\log }_b{x}_2=m\end{array}\right.\Rightarrow \left\{\begin{array}{l}{a}^m=x_1\\ b^m=x_2\end{array}\right.$

Dễ thấy $x_1<x_2\Rightarrow a^m<b^m$

$\Rightarrow a<b$

Vậy $b>a>c$.

Câu 19. Tìm tất cả các giá trị thực của tham số m để hàm số $y=\frac{1}{\sqrt{2m+1-x}}+{\log }_3\sqrt{x-m}$ xác định trên (2;3).

A. $1\le m\le 2$

B. $1<m\le 2$

C. $-1<m<2$

D. $-1\le m\le 2$

Hiển thị đáp án

Đáp án: A

Giải thích:

Hàm số xác định $\iff \left\{\begin{array}{l}2m+1-x>0\\ x-m>0\end{array}\right.$$\iff \left\{\begin{array}{l}x<2m+1\\ x>m\end{array}\right.$

Suy ra, tập xác định của hàm số là $D=\left(m;2m+1\right)$, với $m\ge -1$.

Hàm số xác định trên (2;3) suy ra $\left(2;3\right)\subset D\iff \left\{\begin{array}{l}m\le 2\\ 2m+1\ge 3\end{array}\right.$$\iff \left\{\begin{array}{l}m\le 2\\ m\ge 1\end{array}\right.$.

Câu 20. Cho giới hạn $I=\underset{x\to 0}{\lim }\frac{e^{3x}-e^{2x}}{x}$, chọn mệnh đề đúng:

A. $I^2+3I=2$

B. $I^3+I^2-2=0$

C. $\frac{I-1}{I+1}=1$

D. $3I-2=2I^2$

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có:

$I=\underset{x\to 0}{\lim }\frac{e^{3x}-e^{2x}}{x}$

$=\underset{x\to 0}{\lim }\frac{\left(e^{3x}-1\right)-\left(e^{2x}-1\right)}{x}$

$=\underset{x\to 0}{\lim }\left[3.\frac{e^{3x}-1}{3x}-2\frac{e^{2x}-1}{2x}\right]$

$=3.1-2.1=1$

Do đó, thay I = 1 vào các đáp án ta được đáp án B.

Câu 21. Cho a, b là hai số thực thỏa mãn $a^{\frac{\sqrt{3}}{3}}>a^{\frac{\sqrt{2}}{2}}$ và ${\log }_b\frac{3}{4}<{\log }_b\frac{4}{5}$. Mệnh đề nào sau đây là đúng?

A. $0<a<1,0<b<1$

B. $0<a<1<b$

C. $0<b<1<a$

D. $a>1,b>1$

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có: $\frac{\sqrt{3}}{3}<\frac{\sqrt{2}}{2}$ mà $a^{\frac{\sqrt{3}}{3}}>a^{\frac{\sqrt{2}}{2}}$

Suy ra hàm đặc trưng $y=a^x$ nghịch biến nên $0<a<1$

Vì $\frac{3}{4}<\frac{4}{5}$ và ${\log }_b\frac{3}{4}<{\log }_b\frac{4}{5}$ nên b > 1.

Vậy $0<a<1$ và b > 1 hay $0<a<1<b$

Câu 22. Cho hàm số $f\left(x\right)=2^x{.7}^{x^2}$. Khẳng định nào sau đây sai?

A. $f\left(x\right)<1\iff x+x^2{\log }_{2}7<0$

B. $f\left(x\right)<1\iff x\ln 2+x^2\ln 7<0$

C. $f\left(x\right)<1\iff x{\log }_{7}2+x^2<0$

D. $f\left(x\right)<1\iff 1+x{\log }_{2}7<0$

Hiển thị đáp án

Đáp án: D

Giải thích:

$f\left(x\right)<1\iff 2^x{.7}^{x^2}<1$

$\iff 7^{x^2}<2^{-x}$

$\iff x^2.\ln 7<-x.\ln 2$

$\iff x\ln 2+x^2\ln 7<0$

$\iff x+x^2{\log }_{2}7<0$

$\iff x{\log }_{7}2+x^2<0$

Đối chiếu các đáp án thấy câu D sai.

Câu 23. Cho các số thực dương a, b khác 1. Biết rằng đường thẳng y = 2 cắt đồ thị các hàm số $y=a^x;y=b^x$ và trục tung lần lượt tại A, B, C nằm giữa A và B, và AC = 2BC. Khẳng định nào dưới đây đúng?

A. $b=\frac{a}{2}$

B. $b=2a$

C. $b=a^{-2}$

D. $b=a^2$

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có: $C\left(0;2\right)$

$a^x=2\Rightarrow x={\log }_{a}2$

$\Rightarrow A\left({\log }_{a}2;2\right)$

$b^x=2\Rightarrow x={\log }_{b}2$

$\Rightarrow B\left({\log }_{b}2;2\right)$

Vì C nằm giữa A và B và:

$AC=2BC$

$\iff \overrightarrow{AC}=-2\overrightarrow{BC}$

$\iff \left\{\begin{array}{c}-{\log }_{a}2=2.{\log }_{b}2\\ 0=0\end{array}\right.$

$\iff -\frac{1}{{\log }_{2}a}=2.\frac{1}{{\log }_{2}b}$

$\iff {\log }_{2}b={\log }_2{a}^{-2}$

$\iff b=a^{-2}$

Câu 24. Gọi m là GTNN của hàm số $f\left(x\right)=e^{x^3-3x+3}$ trên đoạn $\left[0;2\right]$. Chọn kết luận đúng:

A. $m=e$

B. $m=e^2$

C. $m=e^3$

D. $m=e^5$

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có: $f\text{'}\left(x\right)=\left(3x^2-3\right)e^{x^3-3x+3}=0$

$\iff 3x^2-3=0$

$\iff \left[\begin{array}{c}x=1\in \left[0;2\right]\\ x=-1\notin \left[0;2\right]\end{array}\right.$

$f\left(0\right)=e^3;f\left(1\right)=e;f\left(2\right)=e^5$ nên $\underset{\left[0;2\right]}{\min }f\left(x\right)=f\left(1\right)=e$ và $\underset{\left[0;2\right]}{\mathrm{m}ax}f\left(x\right)=f\left(2\right)=e^5$

Vậy $m=e$

Câu 25. Hình bên là đồ thị của ba hàm số $y=a^x$, $y=b^x$, $y=c^x$ $\left(0<a,b,c\ne 1\right)$ được vẽ trên cùng một hệ trục tọa độ. Khẳng định nào sau đây là khẳng định đúng?

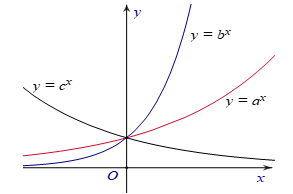
A. $b>a>c$

B. $a>b>c$

C. $a>c>b$

D.$c>b>a$

Hiển thị đáp án

Đáp án: A

Giải thích:

Do $y=a^x$ và $y=b^x$ là hai hàm đồng biến nên $a,b>1$.

Do $y=c^x$ nghịch biến nên $c<1$. Vậy x bé nhất.

Mặt khác: Lấy $x=m$, khi đó tồn tại $y_1,{\text{ y}}_2>0$ để $\left\{\begin{array}{l}{a}^m=y_1\\ b^m=y_2\end{array}\right.$

Dễ thấy $y_1<y_2\Rightarrow a^m<b^m$

$\Rightarrow a<b$

Vậy $b>a>c$.

Câu 26. Tìm đạo hàm của hàm số y = x.2^3x

A. y' = 2^3x(1 + 3xln2)

B. y' = 2^3x(1 + xln2)

C. y' = 2^3x(1 + 3ln3)

D. y' = 2^3x(1 + xln3)

Hiển thị đáp án

Đáp án: A

Giải thích:

y' = 2^3x + x.2^3x.ln(2)3 = 2^3x(1 + 3xln2)

Câu 27. Tính đạo hàm của hàm số

Hiển thị đáp án

Đáp án: C

Giải thích:

Câu 28. Tìm đạo hàm của hàm số

Hiển thị đáp án

Đáp án: B

Giải thích:

Để thuận tiện, ta viết lại

Câu 29. Viết phương trình tiếp tuyến của đồ thị hàm số y = xe^-2x + 2 tại giao điểm của đồ thị hàm số với trục tung

A. y = x + 2

B. y = x

C. y = 2x + 2

D. y = -2x + 2

Hiển thị đáp án

Đáp án: A

Giải thích:

Đồ thị hàm số cắt trục tung tại điểm A(0 ; 2).

y' = e^-2x(1 - 2x); y'(0) = 1, y(0) = 2. Phương trình tiếp tuyến cần tìm: y = 1(x - 0) + 2 hay y = x + 2

Câu 30. Tìm các khoảng đồng biến của hàm số y = 4x - 5ln(x² + 1)

Hiển thị đáp án

Đáp án: C

Giải thích:

Tập xác định : R

Bảng xét dấu

Khoảng đồng biến của hàm số là (-∞; 1/2) và (2; +∞)

Câu 31. Cho hàm số y = x²e^-x . Khẳng định nào sau đây là đúng ?

A. Hàm số có x = 0 là điểm cực đại, x = 2 là điểm cực tiểu

B. Hàm số có x = 0 là điểm cực tiểu, x = -2 là điểm cực đại

C. Hàm số có x = 0 là điểm cực đại, x = -2 là điểm cực tiểu

D. Hàm số có x = 0 là điểm cực tiểu, x = 2 là điểm cực đại

Hiển thị đáp án

Đáp án: D

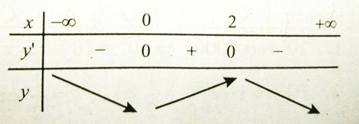
Giải thích:

y' = e^-xx(2 - x). Bảng biến thiên

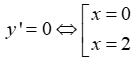
Từ bảng biến thiên ta thấy x = 0 là điểm cực tiểu, x = 2 là điểm cực đại của hàm số.

Câu 32. Tìm các đường tiệm cận ngang của đồ thị hàm số

A. y = 0

B. y = 3

C. y = 0 và y = 3/2

D. y = 0 và y = 3

Hiển thị đáp án

Đáp án: C

Giải thích:

Từ đó suy ra hàm số có hai tiệm cận ngang là y = 3/2 và y = 0

Vậy đồ thị hàm số đã cho có 2 tiệm cận ngang là: y = 3/2; y = 0

Câu 33. Một quần thể vi khuẩn lúc đầu có 200 cá thể và cứ sau một ngày thì số lượng cá thể tăng lên gấp ba lần. Tìm công thức biểu thị số lượng cá thể (kí hiệu N) của quần thể này sau t ngày kể từ lúc ban đầu.

A. N(t) = 200.t³

B. N(t) = 200.3^t

C. N(t) = 200.e^3t

D. N(t) = 200.e^t/3

Hiển thị đáp án

Đáp án: B

Giải thích:

Theo giả thiết, số lượng vi khuẩn sau 1, 2, 3,… ngày là 200.3 ; 200 .3.3 ; 200.3.3.3 ;… Từ đó ta thấy công thức đúng là N(t) = 200.3^t

Câu 34. Số lượng cá thể của một loài sinh vật bị suy giảm trong 10 năm theo cách : số lượng năm sau bằng 95% số lượng năm trước đó. Tại thời điểm chọn làm mốc thời gian loài này có 5000 cá thể. Công thức nào sau đây diễn tả số lượng cá thể (kí hiệu N) của loài theo thời gian t (tính bằng năm, 0 ≤ t ≤ 10 ) ?

A. N = 5000.(1 + 0,95)^t

B. N = 5000.(0,95)^t

C. N = 5000.e^-0,95t

D. N = 5000.e^-0,05t

Hiển thị đáp án

Đáp án: B

Giải thích:

Tại thời điểm chọn làm mốc thời gian có 5000 cá thể.

Sau 1 năm số lượng cá thể còn lại là 5000. 95% = 0,95. 5000

Sau 2 năm số lượng cá thể còn lại là : (0,95. 5000). 0,95 = 0,952. 5000

...Sau t ( ) năm số lượng cá thể còn lại là : 0,95t. 5000

Câu 35. Một người gửi tiết kiệm vào ngân hàng số tiền 50 triệu đồng với hình thức lãi kép và lãi suất 6,8% một năm. Hỏi sau 3 năm trong tài khoản tiết kiệm của người đó có bao nhiêu tiền (làm tròn kết quả đến hàng nghìn) ?

A. 60200000 đồng

B. 60909000 đồng

C. 61280000 đồng

D. 61315000 đồng

Hiển thị đáp án

Đáp án: B

Giải thích:

Số tiền trong tài khoản người đó sau n năm nếu người đó không rút tiền và lãi suất không thay đôỉ được tính theo công thức : P(t) = 50000000(1 + 0,068)^t (đồng)

Số tiền cần tính : P(3) = 50000000(1 + 0,068)³ ≈ 60909000(đồng)

Câu 36. Cho hai số thực a và b, với 0 < a < 1 < b. Khẳng định nào sau đây là đúng?

A. log_ba + log_ab < 0

B. 0 < log_ba + log_ab < 2

C. log_ba + log_ab = 0

D. log_ba + log_ab ≥ 2

Hiển thị đáp án

Đáp án: A

Giải thích:

Do 0 < a < 1 nên hàm số y = log_ax nghịch biến, còn hàm số y = log_bx đồng biến trên (0; +∞). Ta có log_ab < log_a1 = 0 và log_ba < log_b1 = 0.

Do đó log_ab + log_ba < 0

Câu 37. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x² - 2x + ln(2x + 1) trên [0; 1]

Hiển thị đáp án

Đáp án: C

Giải thích:

Câu 38. Dân số Việt Nam năm 2015 là 91,71 triệu người và tỉ lệ tăng dân số là 1,08%. Hỏi nếu vẫn giữ nguyên tỉ lệ tăng dân số hàng năm này thì năm 2020 dân số Việt Nam sẽ là bao nhiêu (làm tròn kết quả đến hàng chục nghìn) ?

A. 96,66 triệu người

B. 96,77 triệu người

C. 96,80 triệu người

D. 97,85 triệu người

Hiển thị đáp án

Đáp án: C

Giải thích:

Dân số lúc đó: 91,71.e^5.0,0108 ≈ 96,80 triệu người

Câu 39. Giả sử số lượng cá thể trong một mẻ cấy vi khuẩn thay đổi theo thời gian t theo công thức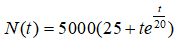 .Tìm số lượng cá thể vi khuẩn lớn nhất (kí hiệu M) và nhỏ nhất (kí hiệu m) của mẻ cấy này trong khoảng thời gian 0 ≤ t ≤ 100

A. M = 161788, m = 128369

B. M = 161788, m = 125000

C. M = 225000, m = 125000

D. M = 225000, m = 128369

Hiển thị đáp án

Đáp án: B

Giải thích:

N'(t) = 250(20 - t)e^-t/20; N'(t) = 0 <=> t = 20

Ta có: N(0) = 125000, N(20) ≈ 161788, N(100) ≈ 128369

Từ đó M = 161788 và m = 125000

Câu 40. Cho hai số thực a và b , với 0 < a < b < 1. Khẳng định nào sau đây là đúng ?

A. log_ba < 1 < log_ab

B. log_ba < log_ab < 1

C. log_ab < 1 < log_ba

D. 1 < log_ab < log_ba

Hiển thị đáp án

Đáp án: C

Giải thích:

Đặt c = b - a ta có c > 0.

Vì 0 < a < b < 1 nên các hàm số y = log_ax và log_bx nghịch biến trên (0; +∞) nên ta có log_ab = log_a(a + c) < log_aa = 1 và log_ba = log_b(b - c) > log_bb = 1.

Vậy log_ab < a < log_ba

Các câu hỏi trắc nghiệm Toán lớp 12 có đáp án, chọn lọc khác:

Trắc nghiệm Phương trình mũ và phương trình Logarit có đáp án

Trắc nghiệm Bất phương trình mũ và bất phương trình Logarit có đáp án

Trắc nghiệm Ôn tập Chương 2 có đáp án

Trắc nghiệm Nguyên hàm có đáp án

Trắc nghiệm Tích phân có đáp án