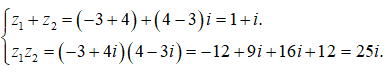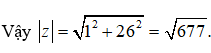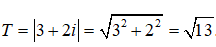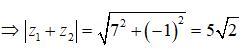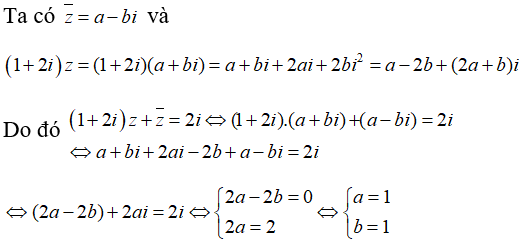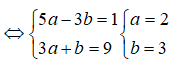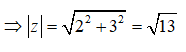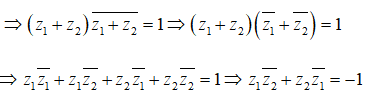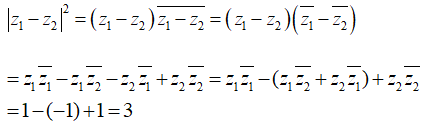Nội dung bài viết

    Xem thêm

    TOP 40 câu Trắc nghiệm Cộng, trừ và nhân số phức (có đáp án 2024) - Toán 12

    Bộ 40 câu hỏi trắc nghiệm Toán lớp 12 Bài 2: Cộng, trừ và nhân số phức có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 12 Bài 2.

    1 717 22/12/2023
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Trắc nghiệm Toán 12 Bài 2: Cộng, trừ và nhân số phức

    Bài giảng Trắc nghiệm Toán 12 Bài 2: Cộng, trừ và nhân số phức

    Câu 1: Tìm số phức z thỏa mãn điều kiện z¯=131−2i¯2−z.

    A. z=−34−2i.

    B. z=−34+2i.

    C. z=2+34i.

    D. z=2−34i.

    Đáp án: A

    Giải thích:

    Ta có z=x+yi x,y∈ℝ

    ⇒x−yi=13[1+2i2−x+yi]

    ⇔3x−yi=−3+4i−x−yi

    =−3−x+(4−y)i

    ⇔{3x=−3−x−3y=4−y

    ⇔{x=−34y=−2

    Câu 2: Rút gọn biểu thức P=1−i2016.

    A. P=21008.

    B. P=-21008.

    C. P=21008i.

    D. P=-21008i.

    Đáp án: A

    Giải thích:

    P=1−i21008=−2i1008

    =22008(i2)504=22008

    Câu 3: Cho số phức z=a+bi, a,b∈ℝ thỏa mãn z=1−i1+i2016. Tính tổng S=a+b.

    A. -1.

    B. 0.

    C. 1.

    D. 2.

    Đáp án: C

    Giải thích:

    Ta có: z=−i1008=i2504=1

    Câu 4: Cho số phức z=a+bi, a,b∈ℝ thỏa mãn z¯=1−2i52+i. Tính tổng S=a+2b.

    A. 38.

    B. 10.

    C. 31.

    D. 55.

    Đáp án: B

    Giải thích:

    z¯=−4+3i1−2i2

    =24+7i

    ⇒z=24−7i

    Câu 5: Cho số phức z=1+z+1+z2+1+i3+...+1+i20.Tìm phần thực a của số phức z

    A. z=1025−1025i.

    B. z=−1025−1025i.

    C. z=−1025+1025i.

    D. z=1025+1025i.

    Đáp án: C

    Giải thích:

    z=1+i.1+i20−11+i−1

    =(1+i).(2i)10−1i

    =(1+i).210.(i2)5−1i

    =−1025+1025i

    Câu 6: Cho số phức z=1+z2+1+i3+...+1+i22. Tìm phần thực a của số phức z.

    A. a=−211

    B. a=−211+2

    C. a=−211−2

    D. a=211.

    Đáp án: C

    Giải thích:

    Ta có: z=1+i.1+i.1+i21−11+i−1

    =2[2i101+i−1]

    =2[210.i251+i−1]

    =2(−1−210−210.i)

    Câu 7: Tìm phần thực a và phần ảo b của số phức z=1+i+i2+i3+...+i2016

    A. a=0, b=−1.

    B. a=0, b=1.

    C. a=1, b=1.

    D. a=1, b=0.

    Đáp án: D

    Giải thích:

    z=1+i.i2016−1i−1

    =1+i.(i2)1008−1i−1

    Câu 8: Tìm môđun của số phức z=1+i2+i4+...+i2n+...+i2016,n∈ℕ

    A. z=2.

    B. z=1.

    C. z=1008.

    D. z=2006.

    Đáp án: B

    Giải thích:

    z=1+i2.i21008−1i2−1=1

    ⇒|z|=1

    Câu 9: Cho số phức z thỏa mãn z−i=z−1+2i. Trong mặt phẳng phức, tập hợp các điểm biểu diễn số phức w=2−iz+1 là một đường thẳng. Viết phương trình đường thẳng đó.

    A. x−7y−9=0

    B. x+7y−9=0

    C. x+7y+9=0

    D. x−7y+9=0

    Đáp án: C

    Giải thích:

    Ta có: w=2−iz+1⇔z=w−12−i

    Suy ra z−i=z−1+2i

    ⇔|w−12−i−i|=|w−12−i−1+2i|

    ⇔w−1−2i+i22−i=w−1−1−2i2−i2−i

    ⇔w−2−2i=w−1+5i

    Đặt w=x+yix;y∈ℝ ta có:

    w−2−2i=w−1+5i

    ⇔(x−2)2+(y−2)2=(x−1)2+(y+5)2

    ⇔2x+14y+18=0

    ⇔x+7y+9=0

    Do đó tập hợp điểm biểu diễn w là đường thẳng x+7y+9=0.

    Câu 10: Cho số phức v=a+bi. Tìm tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức z thỏa mãn điều kiện z−v=1

    A. Đường thẳng x−a+y−b=1

    B. Đường thẳng y=b

    C. Đường tròn x−a2+y−b2=1

    D. Đường thẳng x=a

    Đáp án: C

    Giải thích:

    Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức z thỏa mãn điều kiện z−v=1 là đường tròn tâm Iv=Ia;b bán kính R=1.

    Câu 11: Tìm phần thực a của số phức z=1+1+i+1+i2+1+i3+...+1+i26

    A. a=−213

    B. a=213

    C. a=−1−213

    D. a=1+213.

    Đáp án: B

    Giải thích:

    z=1+1+i.1+i26−11+i−1

    =1+(1+i).(2i)13−1i

    =1+(1+i).213.(i2)6i−1i

    =8192+8193i

    Câu 12: Tính môđun của số phức z thỏa mãn z.z¯+3z−z¯=4−3i

    A. z=2.

    B. z=3.

    C. z=4.

    D. z=1.

    Đáp án: A

    Giải thích:

    a2+b2+3.2bi=4−3i

    ⇔{6b=−3a2+b2=4

    ⇔|z|=a2+b2=2

    Câu 13: Cho số phức z thỏa 1+3iz+2i=−4. Điểm nào sau đây biểu diễn cho z trong các điểm M, N, P, Q ở hình bên?

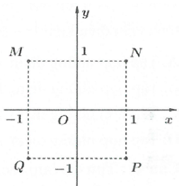
    Trắc nghiệm Cộng, trừ và nhân số phức có đáp án - Toán lớp 12 (ảnh 3)

    A. Điểm M

    B. Điểm N

    C. Điểm P

    D. Điểm Q

    Đáp án: A

    Giải thích:

    Ta có 1+3iz+2i=−4

    ⇔z=−4−2i1+3i⇔z=−1+i

    ⇒(−1;1) là điểm biểu diễn.

    Câu 14: Cho số phức z thỏa z−2+3iz¯=1−9i. Số phức w=5.iz−1 có điểm biểu diễn là điểm nào trong các điểm M, N, P, Q ở hình vẽ?

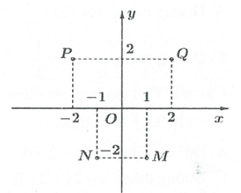
    Trắc nghiệm Cộng, trừ và nhân số phức có đáp án - Toán lớp 12 (ảnh 4)

    A. Điểm N

    B. Điểm Q

    C. Điểm M

    D. Điểm P

    Đáp án: C

    Giải thích:

    Giả sử z=x+yi⇒z¯=x−yi

    Ta có z−2+3iz¯=1−9i

    ⇔(x+yi)−(2+3i)(x−yi)=1−9i

    ⇔x+yi−2x−3y−3xi+2yi=1−9i

    ⇔(−x−3y)+(−3x+3y)i=1−9i

    ⇔−x−3y=1−3x+3y=−9

    ⇔x=2y=−1

    Do đó z=2−i

    ⇒w=5.(iz)−1=5iz

    =5i(2−i)=51+2i=1−2i

    ⇒(1;−2) là điểm biểu diễn.

    Câu 15: Cho số phức z thỏa mãn 3z+2z¯=4−i2. Tính môđun của số phức z.

    A. z=73.

    B. z=5.

    C. z=73.

    D. z=73.

    Đáp án: C

    Giải thích:

    3a+bi+2a−bi=15−8i

    ⇔{3a+2a=153b−2b=−8

    ⇔a=3;b=−8

    ⇒|z|=73

    Câu 16: Cho số phức z thỏa mãn 2z=iz¯+3. Hãy tìm môđun của số phức z.

    A. z=5.

    B. z=5.

    C. z=354.

    D. z=352.

    Đáp án: A

    Giải thích:

    2a+bi=ia+3−bi

    ⇔{2a=b2b=a+3

    ⇔a=1;b=2

    ⇒|z|=5

    Câu 17: Cho số phức z=a+bi a,b∈ℝ thỏa mãn zi+2z¯=4−4i. Tìm 2a+2b.

    A. 2a+2b=136.

    B. 2a+2b=48.

    C. 2a+2b=116.

    D. 2a+2b=32.

    Đáp án: D

    Giải thích:

    a+bi+2a−bi=4−4i

    ⇔{−b+2a=4a−2b=−4

    ⇔a=b=4

    Câu 18: Tìm điểm biểu diễn của số phức z thỏa mãn z=i1+2i2

    A. M1−4;−3

    B. M24;−3

    C. M3−4;3

    D. M44;3

    Đáp án: A

    Giải thích:

    z=i(1+2i)2=i(−3+4i)=−4−3i

    ⇒(−4;−3) là điểm biểu diễn.

    Câu 19: Tìm điểm biểu diễn của số phức z thỏa mãn 9+5iz+7−2i=0

    A. M1;2

    B. N1;1

    C. P2;2

    D. Q−12;12

    Đáp án: D

    Giải thích:

    9+5iz+7−2i=0

    ⇔z=2i−79+5i

    ⇔z=−12+12i

    ⇒(−12;12) là điểm biểu diễn.

    Câu 20: Tìm tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức z thỏa mãn điều kiện là một số thuần ảo v=z−i2+i

    A. Đường tròn x2+y2=2

    B. Đường thẳng x+2y−2=0

    C. Đường thẳng 2x−y+1=0

    D. Đường parabol 2x=y2

    Đáp án: C

    Giải thích:

    Đặt z=x+yix;y∈ℝ ta có: v=z−i2+i

    =(x+yi−i)(2+i)

    Số phức v=z−i2+i là một số thuần ảo khi phần thực 2x−y−1=0 hay 2x−y+1=0.

    Do đó tập hợp điểm biểu diễn số phức z là đường thẳng 2x−y+1=0.

    Câu 21: Trên mặt phẳng tọa độ , tìm tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện số phức w=z2+3i+5−i là số thuần ảo

    A. Đường tròn x2+y2=5

    B. Đường thẳng 2x−3y+5=0

    C. Đường tròn x−32+y−22=5

    D. Đường thẳng 3x+2y−1=0

    Đáp án: B

    Giải thích:

    Đặt z=x+yix;y∈ℝ ta có: w=z2+3i+5−i

    =(x+yi)(2+3i)+5−i

    =2x+2yi+3xi−3y+5−i

    =(2x−3y+5)+(3x+2y−1)i

    Số phức w=z2+3i+5−i là số thuần ảo khi phần thực 2x−3y+5=0

    Do đó tập hợp điểm biểu diễn số phức z là đường thẳng 2x−3y+5=0.

    Câu 22: Tìm tất cả các số phức z thỏa mãn z−2i=5 và điểm biểu diễn của z thuộc đường thẳng d:3x−y+1=0.

    A. z=1−4i

    B. z=1+4i và z=−25−15i

    C. z=−25+15i

    D. z=−1−2i và z=25+115i

    Đáp án: B

    Giải thích:

    Đặt z=x+yix;y∈ℝ ta có: z−2i=5

    ⇔x2+(y−2)2=5

    Giải hệ phương trình x2+y−22=53x−y+1=0

    ⇔{x2+y−22=5y=3x+1

    ⇔{x2+3x+1−22=5y=3x+1

    ⇔10x2−6x−4=0y=3x+1

    ⇔{x=1⇒y=4x=−25⇒y=−15

    Do đó z=1+4i và z=−25−15i là các số phức cần tìm.

    Câu 23: Tập hợp các điểm M biểu diễn số phức z sao cho z2=z¯2 là

    A. Gốc tọa độ

    B. Trục hoành

    C. Trục tung

    D. Trục tung và trục hoành

    Đáp án: D

    Giải thích:

    Đặt z=x+yix;y∈ℝ⇒z¯=x−yi

    ta có: z2=z¯2⇔x+yi2=x−yi2

    Do đó tập hợp điểm biểu diễn số phức z là trục hoành và trục tung.

    Câu 24: Cho hai số phức z1,z2 thỏa mãn z1=z2=1 và z1+z2=3. Tính z1−z2.

    A. 1.

    B. 2.

    C. 3.

    D. 4.

    Đáp án: A

    Giải thích:

    Ta có z1+z22+z1−z22=2z12+z22

    ⇒|z1−z2|=1

    Câu 25: Cho hai số phức z1,z2 thỏa mãn z1+z2=3, z1=1, z2=2. Tính z1.z2¯+z1¯z2.

    A. 2.

    B. 0.

    C. 8.

    D. 4.

    Đáp án: D

    Giải thích:

    Chọn z2=2→z1=1z1+2=3

    Gọi z1=a+bi⇒a2+b2=1a+22+b2=9

    ⇔{a=1b=0

    Vậy z1=1→z1z2¯+z1¯z2

    =1.2+1.2=4

    Câu 26: Cho hai số phức z1 = 2 + 3i, z2 = 1 - 2i . Tìm khẳng định sai

    A. z1 + z2 = 3 + i

    B. z1 - z2 = 1 + 5i

    C. z1.z2 = 8 - i

    D. z1. z2 = 8 + i

    Đáp án: D

    Giải thích:

    Tổng của z1 và z2 là z1 + z2 = (2 + 1) + (3 - 2)i = 3 + i

    Hiệu của z1 và z2 là z1 - z2 = (2 - 1) + (3 + 2)i = 1 + 5i

    Tích của z1 và z2 là z1. z2 = (2 + 3i)(1 - 2i) = 2 - 4i + 3i - 6i2 = 2 - i + 6 = 8 - i

    Câu 27: Cho hai số phức z1= - 3 + 4i, z2 = 4 - 3i . Môđun của số phức z = z1 + z2 + z1. z2 là

    A. 27

    B. √27

    C. √677

    D. 677.

    Đáp án: C

    Giải thích:

    Ta có

    Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

    Do đó z = z1 + z2 + z1. z2 = 1 + i + 25i = 1 + 26i

    Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

    Câu 28: Phần thực và phần ảo của số phức z = (3 + 4i)(4 - 3i) + (2 - i)(3 + 2i) là

    A. 32 và 8i

    B. 32 và 8

    C. 18 và -14

    D. 32 và -8

    Đáp án: B

    Giải thích:

    Ta có z = (12 - 9i + 16i - 12i2) + (6 + 4i - 3i - 2i2) = (12 + 7i + 12) + (6 + i + 2) = 32 + 8i

    Chọn đáp án B.

    Câu 29: Cho các số phức z1 = -1 + i, z2 = 1 - 2i, z3 = 1 + 2i . Giá trị của biểu thức T = |z1z2 + z2z3 + z3z1| là

    A. 1

    B. √13

    C. 5

    D. 13.

    Đáp án: B

    Giải thích:

    Ta có:

    z2z3 = (1 - 2i)(1 + 2i) = 1 - 4i2 = 5

    z1z2 + z1z3 = z1(z2 + z3) = (-1 + i)(1 - 2i + 1 + 2i) = -2 + 2i

    Suy ra Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

    Câu 30: Tổng của hai số phức z1 = 1 - 2i, z2 = 2 - 3i là

    A. 2 + 5i

    B. 2 – 5i

    C. 1 + 5i

    D. 1 – 5i.

    Đáp án: B

    Giải thích:

    Tổng của hai số phức z1 = 1 - 2i, z2 = 1 - 3i là z = (1 + 1) + (-2 - 3)i = 2 - 5i.

    Câu 31: Cho hai số phức z1 = 2 + 3i, z2 = 2 - 4i . Hiệu z1 - z2 bằng

    A. 2 + 7i

    B. 2 – i

    C. 7i

    D. – 7i.

    Đáp án: C

    Giải thích:

    Hiệu của hai số phức z1 = 2 + 3i, z2 = 2 - 4i là z = (2 - 2) + (3 -(-4))i = 7i

    Câu 32: Tích của hai số phức z1 = 3 + 2i, z2 = 2 - 3i là

    A. 6 – 6i

    B. 12

    C. – 5i

    D. 12 – 5i.

    Đáp án: D

    Giải thích:

    Tích của hai số phức z1 = 3 + 2i, z2 = 2 - 3i là:

    z = (3 + 2i)(2 - 3i) = 6 - 9i + 4i - 6i2 = 6 - 5i + 6 = 12 - 5i

    Câu 33: Số phức z = (1 + i)2 bằng

    A. 2i

    B. 1 + 3i

    C. – 2i

    D. 0

    Đáp án: A

    Giải thích: Ta có: z = (1 + i)2 = 1 + 2i + i2 = 1 + 2i - 1 = 2i

    Câu 34: Số phức z = (1 - i)3 bằng

    A. 1 + i

    B. – 2 – 2i

    C. – 2 + 2i

    D. 4 + 4i

    Đáp án: B

    Giải thích:

    Ta có: z = (1 - i)3 = 1 - 3i + 3i2 - i3

    = 1 - 3i - 3.(-1) - i2i = 1 - 3i - 3 + i = -2 - 2i

    Câu 35: Môđun của tổng hai số phức z1 = 3 - 4i và z2 = 4 + 3i là

    A. 5√2

    B. 8

    C. 10

    D. 50.

    Đáp án: A

    Giải thích:

    Ta có: z1 + z2 = (3 + 4) + (-4 + 3)i = 7 - i

    Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

    Câu 36: Cho z = -1 + 3i . Số phức w = iz− + 2z bằng

    A. 1 + 5i

    B. 1 + 7i

    C. – 1 + 5i

    D. – 1 + 7i

    Đáp án: A

    Giải thích:

    Ta có: z = -1 + 3i => z− = -1 - 3i => iz− = - i - 3i2 = 3 - i

    Suy ra: w = 2z + z− = 3 - i + 2(-1 + 3i) = 1 + 5i

    Câu 37: Cho z = 1 + 2i . Phần thực và phần ảo của số phức w = 2z + z− là

    A. 3 và 2

    B. 3 và 2i

    C. 1 và 6

    D. 1 và 6i

    Đáp án: A

    Giải thích:

    Ta có: w = 2z + z− = 2(1 + 2i) + (1 - 2i) = 3 + 2i

    Vậy phần thực của w là 3, phần ảo của w là 2

    Câu 38: Cho số phức z thỏa mãn (1 + 2i)z + iz− = 2i . Khi đó tích z.iz− bằng

    A. – 2

    B. 2

    C. – 2i

    D. 2i.

    Đáp án: B

    Giải thích:

    Đặt z = a + bi(a, b ∈ R).

    Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

    Suy ra z = 1 + i. Vậy z.z− = |z−|2 = 12 + 12 = 2

    Câu 39: Môđun của số phức z thỏa mãn 2z + 3(1 - i)iz− = 1 - 9i là

    A. 5

    B. 13

    C. √5

    D. √13

    Đáp án: D

    Giải thích:

    Đặt z = a + bi (a, b ∈ R).

    Ta có: z− = a - bi và (1 - i)z− = (1 - i)(a - bi) = a - bi - ai + bi2 = a - b - (a + b)i

    Do đó 2z + 3(1 - i)z− = 1 - 9i <=> 2(a + bi) + 3[a - b - (a + b)i] = 1 - 9i

    <=> (5a - 3b) - (3a + b)i = 1 - 9i

    Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

    Suy ra z = 2 + 3i. Vậy:

    Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

    Câu 40: Cho hai số phức z1, z2 thỏa mãn |z1| = |z2| = |z1 + z2| = 1 . Khi đó |z1 - z2| bằng

    A. 0

    B. 1

    C. 2

    D. √3

    Đáp án: D

    Giải thích:

    Ta có: |z1| = |z2| = 1 => z1z1− = z2z2− = 1

    |z1| + |z2| = 1

    Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

    Do đó

    Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

    Vậy |z1| - |z2| = √3

    Các câu hỏi trắc nghiệm Toán lớp 12 có đáp án, chọn lọc khác:

    Trắc nghiệm Ôn tập Chương 3 - Nguyên hàm - Tích phân và ứng dụng có đáp án

    Trắc nghiệm Số phức có đáp án

    Trắc nghiệm Phép chia số phức có đáp án

    Trắc nghiệm Phương trình bậc hai với hệ số thực có đáp án

    Trắc nghiệm Ôn tập Chương 4 có đáp án

    Tham khảo các loạt bài Trắc nghiệm lớp 12 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 717 22/12/2023
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: