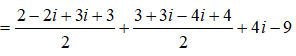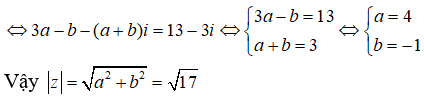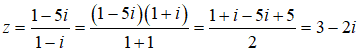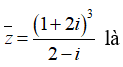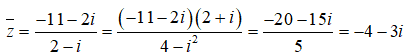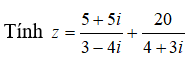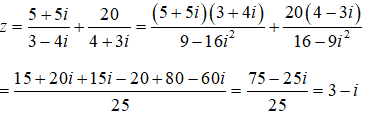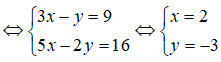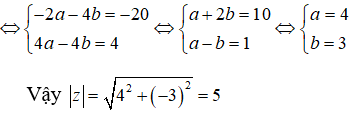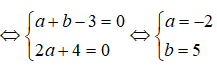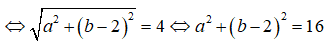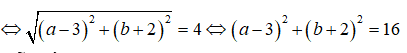TOP 40 câu Trắc nghiệm Ôn tập Chương 4 (có đáp án 2024) - Toán 12
Bộ 40 câu hỏi trắc nghiệm Toán lớp 12 Bài: Ôn tập Chương 4 có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 12 Bài Ôn tập chương 4.
Trắc nghiệm Toán 12 Bài: Ôn tập Chương 4
Câu 1. Thu gọn z=(√2+3i)2 ta được:
A. z=11−6i
B. z=−1−i
C. z=4+3i
D. z=−7+6√2i
Đáp án: D
Giải thích:
Ta có: z=(√2+3i)2=2+6√2i+9i2
=−7+6√2i
Câu 2. Trong các kết luận sau, kết luận nào sai:
A. z+ˉz là một số thực
B. z−ˉz là một số ảo
C. z.ˉz là một số thực
D. z2+ˉz2 là một số ảo
Đáp án: D
Giải thích:
Giả sử z=a+bi(a,b∈R)
⇒ˉz=a−bi
Ta có: z+ˉz=a+bi+a−bi=2a là một số thực
⇒A đúng.
z−ˉz=a+bi−a+bi=2bi là một số ảo
⇒B đúng
z.ˉz=(a+bi).(a−bi)=a2+b2 là một số thực
⇒C đúng
z2+ˉz2=(a+bi)2+(a−bi)2
=2a2−2b2 là một số thực
⇒ D sai
Câu 3. Cho hai số phức z1=1+2i;z2=2−3i. Xác định phần ảo của số phức 3z1−2z2
A. 11
B. 12
C. 10
D. 13
Đáp án: B
Giải thích:
Ta có: z1=1+2i;z2=2−3i
⇒3z1−2z2=3(1+2i)−2(2−3i)
=3+6i−4+6i=−1+12i
Vậy phần ảo của số phức đó là 12.
Câu 4. Tìm số phức liên hợp của số phức z=3+2i
A. ˉz=3−2i
B. ˉz=-3−2i
C. ˉz=2−3i
D. ˉz=−2−3i
Đáp án: A
Giải thích:
Số phức liên hợp của số phức z=3+2i là ˉz=3−2i
Câu 5. Trong hình vẽ bên, điểm M biểu diễn số phức z. Số phức ˉz là:
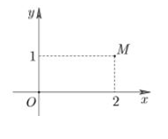
A. 2−i
B. 1+2i
C. 1−2i
D. 2+i
Đáp án: A
Giải thích:
Ta có M(2;1) biểu diễn số phức z ⇒z=2+i⇒ˉz=2−i
Câu 6. Cho số phức z thỏa mãn z(1+i)=3−5i. Tính mô đun của z
A. |z|=√17
B. |z|=16
C. |z|=17
D. |z|=4
Đáp án: A
Giải thích:
Ta có:
z(1+i)=3−5i
⇔z=3−5i1+i=(3−5i)(1−t)1−i2
=−1−4i
⇒|z|=√(−1)2+(−4)2=√17
Câu 7. Phương trình 8z2−4z+1=0 có nghiệm là:
A. z=14+14i;z=54−14i
B. z=14+14i;z=14−34i
C. z=14+14i;z=14−14i
D. z=24+14i;z=14−14i
Đáp án: C
Giải thích:
Phương trình 8z2−4z+1=0
Có Δ'
phương trình có 2 nghiệm là:
Câu 8. Trong C, cho phương trình (*). Gọi , ta xét các mệnh đề sau:
1) Nếu là số thực âm thì phương trình (*) vô nghiệm.
2) Nếu thì phương trình (*) có 2 nghiệm phân biệt
3) Nếu thì phương trình (*) có 1 nghiệm kép
Trong các mệnh đề trên
A. Không có mệnh đề nào đúng
B. Có 1 mệnh đề đúng
C. Có 2 mệnh đề đúng
D. Có 3 mệnh đề đúng
Đáp án: C
Giải thích:
1) Sai vì nếu do đó phương trình có 2 nghiệm phức
2) Đúng
3) Đúng
Vậy có 2 mệnh đề đúng
Câu 9. Phần thực của số phức z thỏa mãn là:
A. – 6
B. – 3
C. 2
D. – 1
Đáp án: C
Giải thích:
Ta có:
Phần thực của số phức z là: 2
Câu 10. Biết số phức thỏa mãn đồng thời các điều kiện và biểu thức đạt giá trị lớn nhất. Tính
A.
B.
C.
D.
Đáp án: D
Giải thích:
Vì
Suy ra tập hợp các điểm biểu diễn số phức z là đường tròn (C) có tâm I (3; 4) và bán kính
Ta có:
Ta tìm P sao cho đường thẳng và đường tròn (C) có điểm chung
Do đó .
Dấu “=” xảy ra
Vậy
Câu 11. Cho hai số phức thỏa mãn . Gọi M, N là các điểm biểu diễn cho và . Biết . Tính ?
A.
B.
C.
D.
Đáp án: B
Giải thích:
Đặt
M, N là các điểm biểu diễn cho
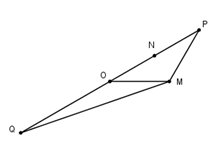
Gọi P là điểm biểu diễn cho và Q là điểm biểu diễn cho , ta có N là trung điểm của OP và P, Q đối xứng nhau qua O. Khi đó
Áp dụng định lí Cosin trong có:
Áp dụng định lí cô sin trong có:
Câu 12. Cho hai số phức thỏa mãn và . Tìm giá trị lớn nhất m của biểu thức
A.
B.
C.
D.
Đáp án: B
Giải thích:
Ta có:
Lại có:
Câu 13. Điểm biểu diễn của số phức z là . Tọa độ của điểm biểu diễn số phức là:
A. (2;-3)
B. (2;1)
C. (-1;6)
D. (2;3)
Đáp án: C
Giải thích:
Điểm biểu diễn của số phức z là
Điểm biểu diễn của số phức là
Câu 14. Gọi lần lượt là hai nghiệm của phương trình với có phần ảo dương. Giá trị của biểu thức bằng
A. 9 + 4i
B. – 10 + 10i
C. – 5
D. 10
Đáp án: A
Giải thích:
Câu 15. Tổng phần thực và phần ảo của số phức z thỏa mãn bằng:
A. 2
B. – 2
C. 6
D. – 6
Đáp án: C
Giải thích:
Đặt
Tổng của phần thực và phần ảo là: 6
Câu 16. Giả sử là hai nghiệm phức của phương trình và A, B là các điểm biểu diễn của . Tọa độ trung điểm của đoạn thẳng AB là:
A. (0;1)
B. (0;-1)
C. (1;1)
D. (1;0)
Đáp án: D
Giải thích:
Phương trình:
Có:
Phương trình có 2 nghiệm là:
Khi đó
Tọa độ trung điểm đoạn thẳng AB là (1;0)
Câu 17. Phương trình bậc hai nào sau đây có nghiệm là ?
A.
B.
C.
D.
Đáp án: C
Giải thích:
+ Xét phương trình
Loại đáp án A.
+ Xét phương trình
Loại đáp án B.
+ Xét phương trình
Chọn đáp án C.
Câu 18. Có bao nhiêu số phức z thỏa mãn đồng thời các điều kiện
A. 1
B. 2
C. 3
D. 4
Đáp án: B
Giải thích:
Giả sử số phức cần tìm là
Từ điều kiện ta có
Từ điều kiện
Câu 19. Có bao nhiêu số phức z thỏa mãn
A. 4
B. 3
C. 2
D. 1
Đáp án: D
Giải thích:
Đặt , khi đó ta có:
Câu 20. Trong mặt phẳng tọa độ Oxy, tập hợp các điểm biểu diễn số phức z thỏa mãn là số thực là:
A. Đường tròn bán kính bằng 1
B. Trục Ox
C. Đường thẳng y = - x
D. Đường thẳng y = x
Đáp án: C
Giải thích:
Giả sử ta có số phức .
Ta có:
là số thực khi x + y = 0 hay y = -x
Câu 21. Các nghiệm là nghiệm của phương trình nào sau đây?
A.
B.
C.
D.
Đáp án: B
Giải thích:
Ta có:
là các nghiệm của phương trình
Câu 22. Cho số phức z thỏa mãn . Biết rằng tập hợp điểm trong mặt phẳng tọa độ biểu diễn các số phức z là một đường tròn. Tìm tọa độ tâm I và bán kính của đường tròn đó.
A.
B.
C.
D.
Đáp án: D
Giải thích:
Giả sử
Theo đề bài ta có:
Vậy tập hợp điểm trong mặt phẳng tọa độ biểu diễn các số phức z là đường tròn tâm
Câu 23. Tìm số điểm biểu diễn cho số phức z thỏa mãn đồng thời các điều kiện và z là thuần ảo?
A. 1
B. 0
C. 3
D. 2
Đáp án: D
Giải thích:
Vì z là thuần ảo nên .
Từ điều kiện có:
Mỗi một số phức z chỉ có 1 điểm biểu diễn trên mặt phẳng phức.
Vậy có hai số phức z thỏa mãn đề bài tương ứng với hai đểm biểu diễn.
Câu 24. Số số phức z thỏa mãn đồng thời các điều kiện và là số thuần ảo là:
A. 1
B. 4
C. 0
D. 2
Đáp án: B
Giải thích:
Giả sử , ta có
Vì là số thuần ảo nên ta có (1)
Từ điều kiện có (2)
Ta có:
Có 4 bộ số là
Câu 25. Số phức thỏa mãn đồng thời có mô đun nhỏ nhất là:
A.
B.
C.
D.
Đáp án: A
Giải thích:
Từ điều kiện ta có:
Ta có:
Vậy khi hay
Câu 26. Cho các số phức thỏa mãn điều kiện
. Giá trị của biểu thức bằng:
A. 8
B. 6
C. 1
D. 2
Đáp án: D
Giải thích:
Ta có:
Câu 27: Cho hai số phức z1 = 1 + 2i, z2 = 2 - 3i . Phần thực và phần ảo của số phức w = 3z1 - 2z2 là
A. 1 và 12
B. -1 và 12
C. –1 và 12i
D. 1 và 12i.
Đáp án: B
Giải thích:
Ta có: w = 3z1 - 2z2 = 3(1 + 2i) - 2(2 - 3i) = -1 + 2i.
Vậy phần thực và phần ảo của w là -1 và 12
Câu 28: Phần thực và phần ảo của số phức z = (1 + √3i)2 là
A. 1 và 3
B. 1 và -3
C. -2 và 2√3
D. 2 và -2√3 .
Đáp án: C
Giải thích:
Ta có: z = 1 + 2√3 + 3i2 = -2 + 2√3i
Vậy phần thực và phần ảo của z là -2 và 2√3
Câu 29: Phần ảo của số phức z = (1 + √i)3 là
A. 3√3
B. -3√3
C. – 8i
D. –8.
Đáp án: D
Giải thích:
Ta có: z = i(1 + √3i)3 = i(1 + 3√3i - 9 - 3√3i) = -8i .
Vậy phần ảo của z là -8
Câu 30: Thực hiện phép tính: 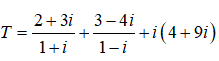
A. T = 3 + 4i
B. T = -3 + 4i
C. T = 3 – 4i
D. T = -3 – 4i.
Đáp án: B
Giải thích:
Ta có:
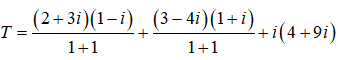
=> T = -3 + 4i
Câu 31: Môđun của số phức z thỏa mãn điều kiện z + (2 - i)z− = 13 - 3i là
A. 3
B. 5
C. 17
D. √17
Đáp án: D
Giải thích:
Môđun của số phức z thỏa mãn điều kiện z + (2 - i)z− = 13 - 3i là:
Đặt z = a + bi(a, b ∈ R). Ta có: z− = a - bi và (2 - i)z− = (2 - i)(a - bi) = 2a - 2bi - ai - b = 2a - b - (2b + a)i
Do đó : z = (2 - i)z− = 13 - 3i ⇔ a + bi + 2a - b - (2b + a)i = 13 - 3i
Câu 32: Phần thực và phần ảo của số phức z thỏa mãn (1 - i)z - 1 + 5i = 0 là
A. 3 và –2
B. 3 và 2
C. 3 và – 2i
D. 3 và 2i.
Đáp án: A
Giải thích:
Ta có: (1 - i)z - 1 + 5i = 0 ⇔ (1 - i)z = 1 - 5i
Vậy phần thực và phần ảo của z là 3 và -2
Câu 33: Giá trị của biểu thức T = i2016 + i216 + i16 + i6 + 1 ta có
A. 3
B. 4
C. 5
D. 6.
Đáp án: A
Giải thích:
Ta có i2 = -1, i4 = 1. Do đó
T = (i4)504 + (i4)54 + (i4)4 + (i2)3 + 1 = 1 + 1 + 1 - 1 + 1 = 3
Câu 34: Số phức z thỏa mãn
A. z = 4 - 3i
B. z = 4 + 3i
C. z = -4 - 3i
D. z = -4 + 3i
Đáp án: D
Giải thích:
Ta có (1 + 2i)3 = 1 + 6i + 12i2 + 8i3 = 1 + 6i - 12 - 8i = -11 - 2i. Do đó:
Vậy: z = -4 + 3i
Câu 35:
A. z = 3 - i
B. z = 3 + i
C. z = -3 + i
D. z = -3 - i
Đáp án: A
Giải thích:
Ta có
Câu 36: Các số thực x, y thỏa mãn đẳng thức x(3 + 5i) - y(1 + 2i) = 9 + 16i . Giá trị biểu thức T = |x - y| là
A. 0
B. 1
C. 3
D. 5.
Đáp án: D
Giải thích:
Ta có: x(3 + 5i) - y(1 + 2i) = 9 + 16i <=> (3x - y) + (5x - 2y) = 9 + 16i
Vậy: T = |x - y| = 5
Câu 37: Cho số phức z thỏa mãn (1 + 2i)2.z + z− = 4i - 20. Môđun của z là
A. 4
B. 5
C. 6
D. 10
Đáp án: B
Giải thích:
Đặt a + bi(a, b ∈R). Ta có:
(1 + 2i)2z = (1 + 2i - 4)(a + bi) = -3a - 3bi + 4ai - 4b = -3a - 4b + (4a - 3b)i
Do đó: (1 + 2i)2.z + a− = 4i - 20 <=> -3a - 4b + (4a - 3b)i + a - bi = 4i - 20
<=> -2a - 4b + (4a - 4b)i = 4i - 20
Câu 38: Phương trình z2 + az + b = 0 nhận z = 1 - 2i làm nghiệm. Khi đó a + b bằng
A. 3
B. 4
C. 5
D. 6.
Đáp án: A
Giải thích:
Ta có z = 1 - 2i là nghiệm của phương trình đã cho nên:
(1 - 2i)2 + a(1 - 2i) + b = 0 <=> (a + b - 3) - (2a + 4)i = 0
Vậy: a + b = -2 + 5 = 3
Câu 39: Tập hợp các điểm biểu diễn số phức z thỏa mãn |z - 2i| = 4 là
A. Đường tròn tâm I(1; -2) bán kính R = 4
B. Đường tròn tâm I(1; 2) bán kính R = 4
C. Đường tròn tâm I(0; 2) bán kính R = 4
D. Đường tròn tâm I(0; -2) bán kính R = 4
Đáp án: C
Giải thích:
Đặt z = a + bi(a, b ∈ R). Ta có:
|z - 2i| = 4 ⇔ |a + (b - 2)i| = 4
Vậy tập các điểm biểu diễn số phức z là đường tròn tâm I(0 ;2), bán kính R = 4
Câu 40: Tập hợp các điểm biểu diễn số phức z thỏa mãn |z− + 3 - 2i| = 4 là
A. Đường tròn tâm I(3; 2) bán kính R = 4
B. Đường tròn tâm I(3; -2) bán kính R = 4
C. Đường tròn tâm I(-3; 2) bán kính R = 4
D. Đường tròn tâm I(-3; -2) bán kính R = 4
Đáp án: D
Giải thích:
Đặt z = a + bi(a, b ∈ R). Ta có: |z− + 3 - 2i| = 4 ⇔ |a - bi + 3 - 2i| = 4
⇔ |(a + 3) - (b + 2)i| = 4
Vậy tập các điểm biểu diễn số phức z là đường tròn tâm I(-3 ;-2), bán kính R = 4
Các câu hỏi trắc nghiệm Toán lớp 12 có đáp án, chọn lọc khác:
Trắc nghiệm Ôn tập Chương 3 - Nguyên hàm - Tích phân và ứng dụng có đáp án
Trắc nghiệm Cộng, trừ và nhân số phức có đáp án
Xem thêm các chương trình khác:
- Trắc nghiệm Sinh học lớp 7 có đáp án
- Trắc nghiệm Toán lớp 7 có đáp án
- Trắc nghiệm Ngữ văn lớp 7 có đáp án
- Trắc nghiệm Sinh học 8 có đáp án
- Trắc nghiệm Toán lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn 8 có đáp án
- Trắc nghiệm Hóa học lớp 8 có đáp án
- Trắc nghiệm Địa Lí lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Tiếng Anh lớp 8 có đáp án
- Trắc nghiệm GDCD lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Lịch sử lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Vật Lí lớp 8 có đáp án
- Trắc nghiệm Công nghệ lớp 8 có đáp án
- Trắc nghiệm Tin học lớp 8 có đáp án
- Trắc nghiệm Sinh học lớp 9 có đáp án
- Trắc nghiệm Toán lớp 9 có đáp án
- Trắc nghiệm Ngữ văn 9 có đáp án
- Trắc nghiệm Hóa học lớp 9 có đáp án
- Trắc nghiệm Địa lí lớp 9 có đáp án
- Trắc nghiệm Tiếng Anh lớp 9 có đáp án
- Trắc nghiệm GDCD lớp 9 có đáp án
- Trắc nghiệm Lịch sử lớp 9 có đáp án
- Trắc nghiệm Vật lí lớp 9 có đáp án
- Trắc nghiệm Công nghệ lớp 9 có đáp án
- Trắc nghiệm Sinh học lớp 10 có đáp án
- Trắc nghiệm Toán lớp 10 có đáp án
- Trắc nghiệm Hóa học lớp 10 có đáp án
- Trắc nghiệm Ngữ văn lớp 10 có đáp án
- Trắc nghiệm Vật Lí lớp 10 có đáp án
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án
- Trắc nghiệm Sinh học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Toán lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Hóa học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn lớp 11 có đáp án
- Trắc nghiệm Tiếng Anh lớp 11 có đáp án
- Trắc nghiệm Vật Lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Địa lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm GDCD lớp 11 có đáp án
- Trắc nghiệm Lịch sử lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Công nghệ lớp 11 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 11 có đáp án
- Trắc nghiệm Tin học lớp 11 có đáp án