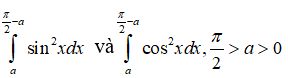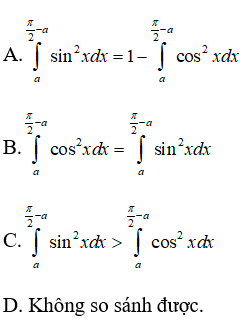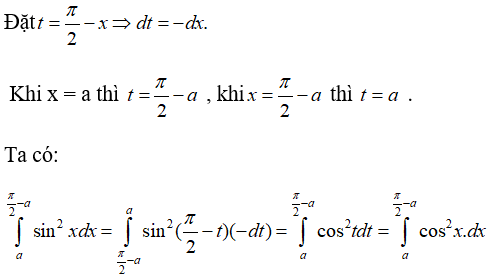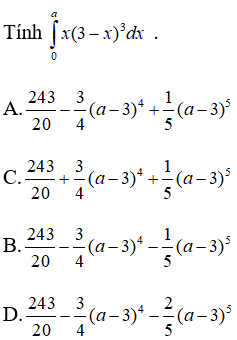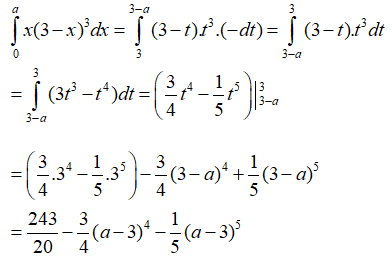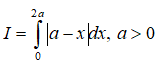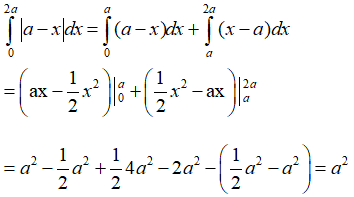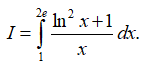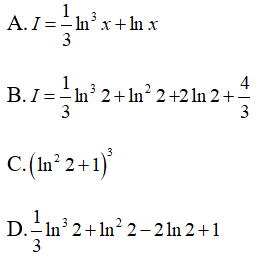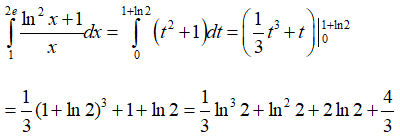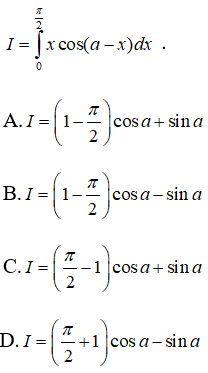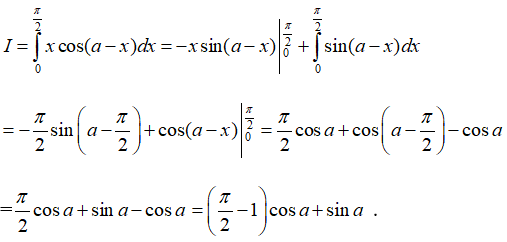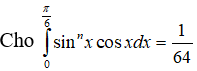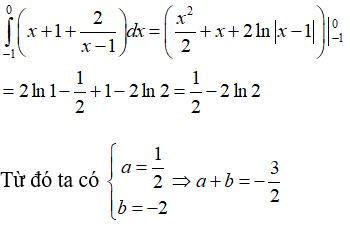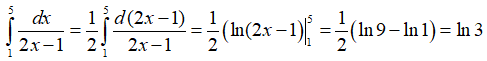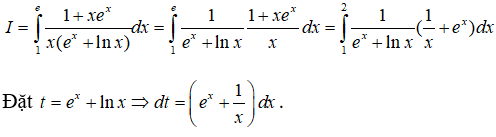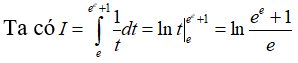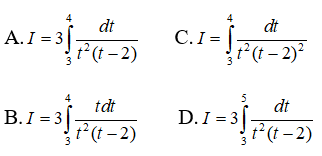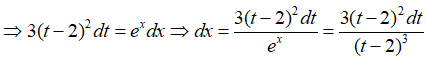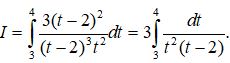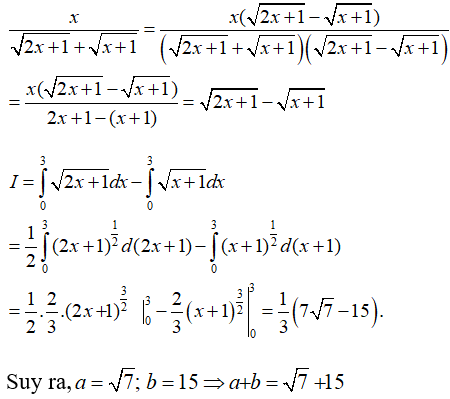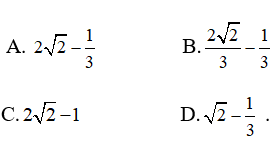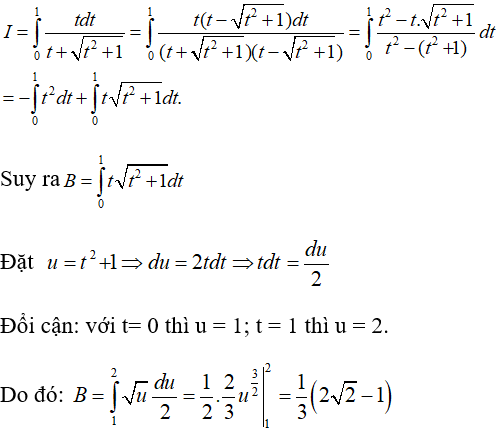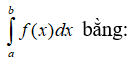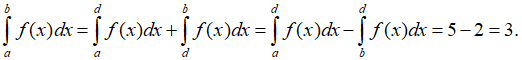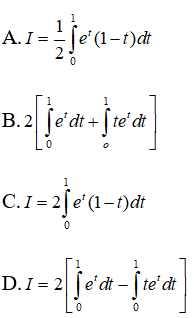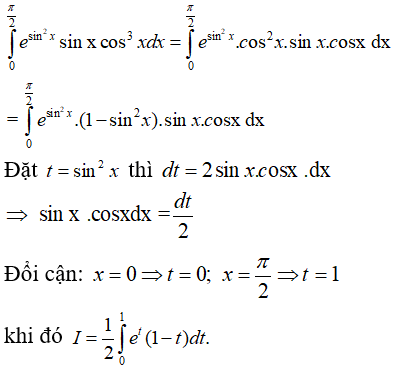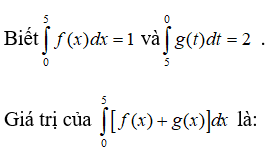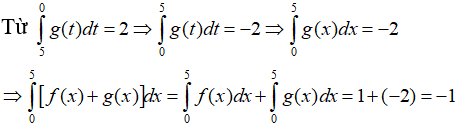TOP 40 câu Trắc nghiệm Tích phân (có đáp án 2024) - Toán 12

Bộ 40 câu hỏi trắc nghiệm Toán lớp 12 Bài 2: Tích phân có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 12 Bài 2.

1 1,857 22/12/2023

Tải về

Trang trước

Trang sau

Trắc nghiệm Toán 12 Bài 2: Tích phân

Bài giảng Trắc nghiệm Toán 12 Bài 2: Tích phân

Câu 1. Cho $\int_{0}^{1} \frac{d x}{x^{2} + 3 x + 2} = a \ln 2 + b \ln 3$ với $a, b$ là các số nguyên. Mệnh đề nào sau đây đúng?

A. $a - 2 b = - 5$ .

B. $a + b = 1$ .

C. $a + 2 b = 4$ .

D. $a - 2 b = 5$ .

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có $\int_{0}^{1} \frac{d x}{x^{2} + 3 x + 2}$

$= \int_{0}^{1} \frac{d x}{(x + 1) (x + 2)}$

$= \int_{0}^{1} (\frac{1}{x + 1} - \frac{1}{x + 2}) d x$

$= (\ln |x + 1| - \ln |x + 2|) |\begin{array}{l} 1 \\ 0 \end{array}$

$= (\ln 2 - \ln 3) - (\ln 1 - \ln 2)$

$= 2 \ln 2 - \ln 3$

Vậy $a = 2; b = - 1$

$\Rightarrow a + b = 1$

Câu 2. Xét tích phân $I = \int_{0}^{4} e^{\sqrt{2 x + 1}} d x$ , nếu đặt $u = \sqrt{2 x + 1}$ thì I bằng

A. $\frac{1}{2} \int_{1}^{3} u e^{u} d u$

B. $\int_{0}^{4} u e^{u} d u$ .

C. $\int_{1}^{3} u e^{u} d u$ .

D. $\frac{1}{2} \int_{1}^{3} e^{u} d u$ .

Hiển thị đáp án

Đáp án: C

Giải thích:

Đặt $\Rightarrow x = \frac{u^{2} - 1}{2} \Rightarrow d x = u d u$ .

Đổi cận: $x = 0 \Rightarrow u = 1$

$x = 4 \Rightarrow u = 3$ .

Do đó $I = \int_{1}^{3} u e^{u} d u$ .

Câu 3. Cho hàm số $f (x)$ có đạo hàm trên $ℝ$ , $f (- 1) = - 2$ và $f (3) = 2$ . Tính $I = \int_{- 1}^{3} f^{'} (x) d x$ .

A. -4.

B. 0.

C. 3.

D. 4.

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có $I = \int_{- 1}^{3} f^{'} (x) d x$

$= f (x) |\begin{matrix} 3 \\ - 1 \end{matrix}$

$= f (3) - f (- 1)$

$= 2 - (- 2) = 4$

Vậy $I = 4$ .

Câu 4. Nếu hàm số $y = f (x)$ có đạo hàm liên tục trên $ℝ$ thỏa mãn $f (0) = 2$ , $\int_{0}^{1} f^{'} (x) d x = 5$ thì

A. $f (1) = 7$

B. $f (1) = 10$

C. $f (1) = - 3$

D. $f (1) = 3$

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có $\int_{0}^{1} f^{'} (x) d x = {f (x)|}_{0}^{1}$

$= f (1) - f (0)$

Suy ra $\int_{0}^{1} f^{'} (x) d x = 5$

$\Leftrightarrow f (1) - f (0) = 5$

$\Leftrightarrow f (1) = f (0) + 5 = 7$

Vậy $f (1) = 7$ .

Câu 5. Cho $\int_{0}^{\frac{1}{2}} f (2 x) d x = 1$ . Tính $I = \int_{0}^{\frac{π}{2}} \cos x f (\sin x) d x$ .

A. 2.

B. 1.

C. -1.

D. -2.

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có:

$\int_{0}^{\frac{1}{2}} f (2 x) d x = 1$

$\Leftrightarrow \frac{1}{2} \int_{0}^{\frac{1}{2}} f (2 x) d (2 x) = 1$

$\Leftrightarrow \int_{0}^{1} f (t) d t = 2$

Đặt $t = \sin x$ . Ta có: $d t = d (\sin x) = \cos x d x$ , $\sin 0 = 0$ và $\sin \frac{π}{2} = 1$ .

Vậy $I = \int_{0}^{\frac{π}{2}} \cos x . f (\sin x) d x$

$= \int_{0}^{1} f (t) d t = 2$ .

Câu 6. Xét $\int_{0}^{1} (x + 1) e^{x^{2} + 2 x} d x$ nếu đặt $t = x^{2} + 2 x$ thì $\int_{0}^{1} (x + 1) e^{x^{2} + 2 x} d x$ bằng

A. $\frac{1}{2} \int_{0}^{3} (t + 1) e^{t} d t$ .

B. $\frac{1}{2} \int_{0}^{3} e^{t} d t$ .

C. $\int_{0}^{1} e^{t} d t$ .

D. $\int_{0}^{1} (t + 1) e^{t} d t$ .

Hiển thị đáp án

Đáp án: B

Giải thích:

Đặt $x^{2} + 2 x = t$

$\Rightarrow (2 x + 2) d x = d t$

$\Rightarrow (x + 1) d x = \frac{d t}{2}$

Đổi cận: $x = 0 \Rightarrow t = 0;$

$x = 1 \Rightarrow t = 3$

Khi đó :

$\int_{0}^{1} (x + 1) e^{x^{2} + 2 x} d x$

$= \int_{0}^{3} \frac{e^{t}}{2} d t = \frac{1}{2} \int_{0}^{3} e^{t} d t$

Câu 7. Biết $\int_{1}^{2} \frac{3 x + 1}{3 x^{2} + x \ln x} d x = \ln (a + \frac{\ln b}{c})$ với $a, b, c \in ℤ^{+}, c \leq 4$ . Tổng $a + b + c$ bằng

A. 7.

B. 6.

C. 8.

D. 9.

Hiển thị đáp án

Đáp án: A

Giải thích:

$\int_{1}^{2} \frac{3 x + 1}{3 x^{2} + x \ln x} d x$

$= \int_{1}^{2} \frac{3 + \frac{1}{x}}{3 x + \ln x} d x$

$= \int_{1}^{2} \frac{1}{3 x + \ln x} d (3 x + \ln x)$

$= {\ln |3 x + \ln x||}_{1}^{2}$

$= \ln (2 + \frac{\ln 2}{3})$

Suy ra $a = 2, b = 2, c = 3$ .

Vậy $a + b + c = 7.$

Câu 8. Cho hàm số $f (x)$ liên tục trên đoạn $[1; 9]$ và thỏa mãn $\int_{0}^{2} x . f (2 x^{2} + 1) d x = 2$ . Khi đó $I = \int_{1}^{9} f (x) d x$ có giá trị

A. 8

B. 4

C. 2

D. 1

Hiển thị đáp án

Đáp án: A

Giải thích:

Xét tích phân $\int_{0}^{2} x . f (2 x^{2} + 1) d x = 2$ .

Đặt $t = 2 x^{2} + 1$

$\Rightarrow dt = 4 x . d x$

$\Rightarrow x . d x = \frac{1}{4} dt$ .

Đổi cận:

Với $x = 0 \Rightarrow t = 1$ .

Với $x = 2 \Rightarrow t = 9$ .

Khi đó $2 = \int_{0}^{2} x . f (2 x^{2} + 1) d x$

$= \frac{1}{4} \int_{1}^{9} f (t) d t$ .

Mà tích phân không phụ thuộc vào biến nên $\int_{1}^{9} f (x) d x = 8$

Câu 9. Với hai hàm số f(x) và g(x) liên tục trên $[a; b]$ , k là một hằng số thực, khẳng định nào sau đây sai ?

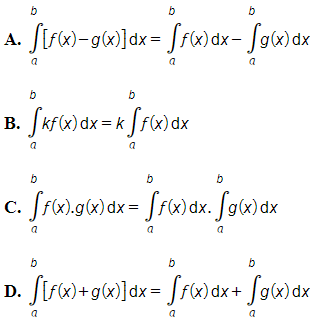
Trắc nghiệm Tích phân có đáp án - Toán lớp 12 (ảnh 1)

Hiển thị đáp án

Đáp án: C

Giải thích:

Theo tính chất của tích phân thì A, B, D đúng, C sai.

Câu 10. Cho $\int_{1}^{2} [4 f (x) - 2 x] d x = 1$ . Khi đó $\int_{1}^{2} f (x) d x$

A. -3.

B. -1.

C. 3.

D. 1.

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có $\int_{1}^{2} [4 f (x) - 2 x] d x$

$= 4 \int_{1}^{2} f (x) d x - 2 \int_{1}^{2} x d x$

$= 4 \int_{1}^{2} f (x) d x - 3$

Theo bài ra: $\int_{1}^{2} [4 f (x) - 2 x] d x = 1$

$\Leftrightarrow 4 \int_{1}^{2} f (x) d x - 3 = 1$

$\Leftrightarrow \int_{1}^{2} f (x) d x = 1$ .

Vậy $\int_{1}^{2} f (x) d x = 1$ .

Câu 11. Cho $a < b < c, \int_{a}^{b} f (x) d x = 5$ và $\int_{c}^{b} f (x) d x = 2$ . Tính $\int_{a}^{c} f (x) d x$ .

A. $\int_{a}^{c} f (x) d x = 3$ .

B. $\int_{a}^{c} f (x) d x = - 2$ .

C. $\int_{a}^{c} f (x) d x = 1$ .

D. $\int_{a}^{c} f (x) d x = 7$ .

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có $\int_{a}^{b} f (x) d x = \int_{a}^{c} f (x) d x + \int_{c}^{b} f (x) d x$

$\Rightarrow 5 {= \int}_{a}^{c} f (x) d x + 2$

$\Rightarrow \int_{a}^{c} f (x) d x = 3$

Vậy $\int_{a}^{c} f (x) d x = 3$ .

Câu 12. Cho hàm số f(x) liên tục trên đoạn $[0; 8]$ , thỏa mãn $\int_{0}^{8} f (x) d x = 9$ và $\int_{0}^{5} f (x) d x = 6$ . Tính $I = \int_{5}^{8} f (x) d x$ .

A. 4.

B. -3.

C. 15.

D. 3.

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có: $\int_{0}^{8} f (x) d x = \int_{0}^{5} f (x) d x + \int_{5}^{8} f (x) d x$

Suy ra: $\int_{5}^{8} f (x) d x = \int_{0}^{8} f (x) d x - \int_{0}^{5} f (x) d x$

$= 9 - 6 = 3$ .

Câu 13. Biết $F (x) = x^{2}$ là một nguyên hàm của hàm số $f (x)$ trên $ℝ$ . Giá trị của bằng

A. $\frac{7}{3}$ .

B. 3.

C. $\frac{13}{3}$ .

D. 5.

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có $\int_{1}^{2} [2 + f (x)] d x = \int_{1}^{2} 2 d x + \int_{1}^{2} f (x) d x$

$= {(2 x)|}_{1}^{2} + {(x^{2})|}_{1}^{2} = 2 + 3 = 5$

Vậy $\int_{1}^{2} [2 + f (x)] d x = 5$ .

Câu 14. Nếu $\int_{1}^{2} f (x) d x = 5$ và $\int_{1}^{2} [2 f (x) + g (x)] d x = 13$ thì $\int_{1}^{2} g (x) d x$ bằng

A. -3.

B. -1.

C. 1.

D. 3.

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có $\int_{1}^{2} [2 f (x) + g (x)] d x = 13$

$\Leftrightarrow 2. \int_{1}^{2} f (x) d x + \int_{1}^{2} g (x) d x = 13$

$\Leftrightarrow \int_{1}^{2} g (x) d x = 13 - 2. \int_{1}^{2} f (x) d x$

$\Leftrightarrow \int_{1}^{2} g (x) d x = 13 - 2.5$

$\Leftrightarrow \int_{1}^{2} g (x) d x = 3$

Vậy $\int_{1}^{2} g (x) d x = 3$ .

Câu 15. Cho hàm số $y = f (x)$ có đạo hàm $f^{'} (x)$ liên tục trên $[0; 2]$ và $f (2) = 3$ , $\int_{0}^{2} f (x) d x = 3$ . Tích phân $\int_{0}^{2} x . f^{'} (x) d x$ bằng

A. 6

B. 3

C. -3

D. 0

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có: $I = \int_{0}^{2} x . f^{'} (x) d x$

$= \int_{0}^{2} x d (f (x))$

$= x . f (x) |\begin{array}{l} 2 \\ 0 \end{array} - \int_{0}^{2} f (x) d x$

$= 2 f (2) - 3$

$= 2.3 - 3 = 3$

Vậy $\int_{0}^{2} x . f^{'} (x) d x = 3$ .

Câu 16. Biết tích phân $\int_{1}^{2} (4 x - 1) \ln x d x = a \ln 2 + b$ với $a, b \in Z$ . Tổng $2 a + b$ bằng

A. 5.

B. 8.

C. 10.

D. 13.

Hiển thị đáp án

Đáp án: C

Giải thích:

Đặt $\{\begin{cases} u = \ln x \\ d v = (4 x - 1) d x \end{cases}$

$\Rightarrow \{\begin{cases} d u = \frac{1}{x} d x \\ v = 2 x^{2} - x = x (2 x - 1) \end{cases}$

Ta có:

$\int_{1}^{2} (4 x - 1) \ln x d x$

$= {x (2 x - 1) \ln x|}_{1}^{2} - \int_{1}^{2} (2 x - 1) d x$

$= 6 \ln 2 - {(x^{2} - x)|}_{1}^{2}$

$= 6 \ln 2 - 2$ .

Vậy $2 a + b = 10$ .

Câu 17. Cho hàm số $f (x)$ có đạo hàm $f^{'} (x)$ và thỏa mãn $\int_{0}^{1} (2 x + 1) f^{'} (x) d x = 10$ , $3 f (1) - f (0) = 12$ . Tính $I = \int_{0}^{1} f (x) d x$ .

A. 1

B. -2

C. 2

D. -1

Hiển thị đáp án

Đáp án: A

Giải thích:

Đặt: $u = 2 x + 1 \Leftrightarrow d u = 2 d x$ , $d v = f^{'} (x) d x$ chọn $v = f (x)$ .

Ta có: $\int_{0}^{1} (2 x + 1) f^{'} (x) d x = 10$

$\Leftrightarrow (2 x + 1) f (x) |\begin{array}{l} 1 \\ 0 \end{array} - 2 \int_{0}^{1} f (x) d x = 10$

$\Leftrightarrow 3 f (1) - f (0) - 2 \int_{0}^{1} f (x) d x = 10$

$\Leftrightarrow 12 - 2 \int_{0}^{1} f (x) d x = 10$

$\Leftrightarrow \int_{0}^{1} f (x) d x = 1$

Câu 18. Biết rằng $I = \int_{2}^{3} \frac{x^{2} - 2 x - 3}{(x - 1) (x^{2} - x + 4)} d x$ $= a \ln 2 + b \ln 3 + c \ln 5, (a, b, c \in ℤ)$ . Tính $S = 2 a - 3 b + 8 c$ .

A. $S = 9$ .

B. $S = - 9$ .

C. $S = 8$ .

D. $S = - 8$ .

Hiển thị đáp án

Đáp án: A

Giải thích:

$I = \int_{2}^{3} \frac{x^{2} - 2 x - 3}{(x - 1) (x^{2} - x + 4)} d x$

$= \int_{2}^{3} (\frac{2 x - 1}{x^{2} - x + 4} - \frac{1}{x - 1}) d x$

$= \int_{2}^{3} \frac{d (x^{2} - x + 4)}{x^{2} - x + 4} d x - \int_{2}^{3} \frac{d x}{x - 1} d x$

$= {\ln |x^{2} - x + 4||}_{2}^{3} - {\ln (x - 1)|}_{2}^{3}$

$= - \ln 2 - \ln 3 + \ln 5$

Như vậy, $a = - 1, b = - 1, c = 1$

Vậy $S = 2 a - 3 b + 8 c = 9$ .

Câu 19. Biết $\int_{0}^{\frac{π}{4}} \frac{1}{1 + \tan x} d x = a π + b \ln 2$ với $a, b$ là các số hữu tỉ. Tính tỷ số $\frac{a}{b}$ .

A. $\frac{1}{2}$ .

B. $\frac{1}{6}$ .

C. $\frac{1}{4}$ .

D. $\frac{1}{3}$ .

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có

$\int_{0}^{\frac{π}{4}} \frac{1}{1 + \tan x} d x$

$= \int_{0}^{\frac{π}{4}} \frac{\cos x}{\sin x + \cos x} d x$

$= \frac{1}{2} \int_{0}^{\frac{π}{4}} \frac{(\sin x + \cos x) + (\cos x - \sin x)}{\sin x + \cos x} d x$

$= \frac{1}{2} (\int_{0}^{\frac{π}{4}} d x + \int_{0}^{\frac{π}{4}} \frac{d (\sin x + \cos x)}{\sin x + \cos x})$

$= \frac{1}{2} (x + \ln |\sin x + \cos x|) |_{0}^{\frac{π}{4}}$

$= \frac{1}{8} π + \frac{1}{4} \ln 2$

$\Rightarrow \{\begin{cases} a = \frac{1}{8} \\ b = \frac{1}{4} \end{cases}$

$\Rightarrow \frac{a}{b} = \frac{1}{2}$

Câu 20. Cho hàm số $f (x)$ có $f (\frac{π}{2}) = 0$ và $f^{'} (x) = cos 2 x . \sin^{3} x$ . Khi đó $\int_{0}^{\frac{π}{6}} f (x) d x$ bằng

A. $\frac{253 π}{1200}$ .

B. $\frac{251}{1200}$ .

C. $\frac{251 π}{1200}$ .

D. $\frac{253}{1200}$ .

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có $f (x) = \int cos 2 x . \sin^{3} x d x$

$= \int (2 {cos}^{2} x - 1) (1 - {cos}^{2} x) \sin x d x$

Đặt $t = cos x$

$\Rightarrow d t = - \sin x d x$

Khi đó: $\int (2 {cos}^{2} x - 1) (1 - {cos}^{2} x) \sin x d x$

$= - \int (2 t^{2} - 1) (1 - t^{2}) d t$

$= \int (2 t^{4} - 3 t^{2} + 1) d t$

$= \frac{2}{5} t^{5} - t^{3} + t + C$

$= \frac{2}{5} {cos}^{5} x - {cos}^{3} x + cos x + C$

Suy ra:

$f (x) = \frac{2}{5} {cos}^{5} x - {cos}^{3} x + cos x + C$

Mà $f (\frac{π}{2}) = 0 \Leftrightarrow C = 0$

Do đó

$f (x) = \frac{2}{5} {cos}^{5} x - {cos}^{3} x + cos x$

$= cos x (\frac{2}{5} {cos}^{4} x - {cos}^{2} x + 1)$

$= cos x [\frac{2}{5} {(1 - {sin}^{2} x)}^{2} + {sin}^{2} x]$

$I = \int_{0}^{\frac{π}{6}} f (x) d x$

$= \int_{0}^{\frac{π}{6}} cos x [\frac{2}{5} {(1 - {sin}^{2} x)}^{2} + {sin}^{2} x] d x$

Đặt $t = \sin x \Rightarrow d t = cos x d x$

Đổi cận

$\{\begin{cases} x = 0 \Rightarrow t = 0 \\ x = \frac{π}{6} \Rightarrow t = \frac{1}{2} \end{cases}$

$I = \int_{0}^{\frac{1}{2}} [\frac{2}{5} {(1 - t^{2})}^{2} + t^{2}] d t$

$= \frac{1}{5} \int_{0}^{\frac{1}{2}} (2 t^{4} + t^{2} + 2) d t$

$= \frac{1}{5} {(\frac{2}{5} t^{5} + \frac{1}{3} t^{3} + 2 t)|}_{0}^{\frac{1}{2}}$

$= \frac{253}{1200}$

Câu 21. Tính tích phân $I = \int_{- 1}^{0} (2 x + 1) d x$ .

A. 0.

B. 1.

C. 2.

D. $- \frac{1}{2}$ .

Hiển thị đáp án

Đáp án: A

Giải thích:

$I = \int_{- 1}^{0} (2 x + 1) d x$

$= {(x^{2} + x)|}_{- 1}^{0} = 0$

Câu 22. Tích phân $\int_{1}^{2} e^{3 x - 1} d x$ bằng:

A. $\frac{1}{3} (e^{5} - e^{2})$ .

B. $\frac{1}{3} (e^{5} + e^{2})$ .

C. $\frac{1}{3} e^{5} - e^{2}$ .

D. $e^{5} - e^{2}$ .

Hiển thị đáp án

Đáp án: A

Giải thích:

$\int_{1}^{2} e^{3 x - 1} d x = \frac{1}{3} \int_{1}^{2} e^{3 x - 1} d (3 x - 1)$

$= {\frac{1}{3} e^{3 x - 1}|}_{1}^{2} = \frac{1}{3} (e^{5} - e^{2})$

Câu 23. Khẳng định nào dưới đây đúng?

A. $\int_{1}^{2} \frac{1}{e^{x}} d x = {\frac{1}{e^{x}}|}_{1}^{2}$ .

B. $\int_{1}^{2} \frac{1}{e^{x}} d x = {e^{x}|}_{2}^{1}$ .

C. $\int_{1}^{2} \frac{1}{e^{x}} d x = {e^{x}|}_{1}^{2}$ .

D. $\int_{1}^{2} \frac{1}{e^{x}} d x = {\frac{1}{e^{x}}|}_{2}^{1}$ .

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có $\int_{1}^{2} \frac{1}{e^{x}} d x = \int_{1}^{2} e^{- x} d x$

$= {- e^{- x}|}_{1}^{2} = {\frac{1}{e^{x}}|}_{2}^{1}$

Câu 24. Tích phân $\int_{0}^{2020} 5^{x} d x$ bằng

A. $\frac{5^{2020} - \ln 5}{5}$ .

B. $\frac{5^{2020} - 5}{\ln 5}$ .

C. $\frac{5^{2021} - \ln 5}{5}$ .

D. $\frac{5^{2020} - 1}{\ln 5}$ .

Hiển thị đáp án

Đáp án: D

Giải thích:

$\int_{0}^{2020} 5^{x} d x = {\frac{5^{x}}{\ln 5}|}_{0}^{2020}$

$= \frac{5^{2020} - 1}{\ln 5}$

Câu 25: Cho số thực a thỏa mãn $\int_{- a}^{1} e^{x + 1} d x = e^{2} - 1$ , khi đó a có giá trị bằng

A. 1

B. -1

C. 0

D. 2

Hiển thị đáp án

Đáp án: A

Giải thích:

Câu 26: Cho hai tích phân:

Trong các khẳng định sau , khẳng định nào đúng?

Hiển thị đáp án

Đáp án: B

Giải thích:

Đặt t = π/2 - x ⇒ dt = -dx Khi x = a thì t = π/2 - a , khi x = π/2 - a thì t = a

Ta có:

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Vậy chọn đáp án B.

Câu 27:

Hiển thị đáp án

Đáp án: B

Giải thích:

Đặt: t = 3 - x ⇒ dt = - dx .

Khi x = 0 thì t = 3, khi x = a thì t = 3-a.

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Vậy chọn đáp án B.

Câu 28: Tính tích phân

A. I = 0

B. I = a²

C. I = -a²

D. I = 2a² .

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có:

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Vậy chọn đáp án B.

Câu 29: Tính tích phân Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Hiển thị đáp án

Đáp án: D

Giải thích:

Đặt t = lnx ⇒ dt = (1/x)dx . Khi x = 1 thì t = 0, khi x = 2e thì t = 1+ln2. Ta có:

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Vậy chọn đáp án D.

Câu 30: Tính tích phân

Hiển thị đáp án

Đáp án: C

Giải thích:

Đặt u = x và dv = cos(a - x)dx ,suy ra du = dx và v = -sin(a-x). Do đó

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Vậy chọn đáp án C.

Câu 31:

Tìm n?

A.6

B.5

C.4

D.3

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có:

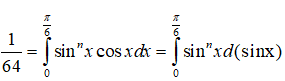
Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Vậy chọn đáp án D.

Câu 32: Kết quả của tích phân 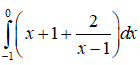được viết dưới dạng a+bln2. Tính giá trị của a+b.

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có:

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Vậy chọn đáp án D

Câu 33: Giả sử 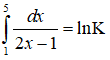.Giá trị của K là:

A.9

B.3

C.81

D.8

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có:

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Do đó, K = 3

Câu 34: Cho: 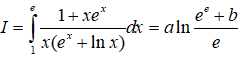Tính giá trị của a-b.

A.3

B.1

C.2

D.0.

Hiển thị đáp án

Đáp án: D

Giải thích:

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Khi x = 1 thì t = e, khi x = e thì t = e^e + 1 .

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Từ đó suy ra: a = 1; b = 1 nên a – b = 0.

Câu 35: Cho 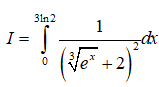Giả sử đặt t = ∛e^x + 2 thì ta được:

Hiển thị đáp án

Đáp án: D

Giải thích:

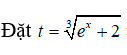
Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12 ⇒(t - 2)³ = e^x

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Đổi cận: x = 0 thì t = 3 ; x = 3ln2 thì t = 4

Khi đó

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Câu 36: Cho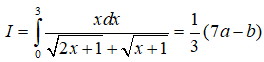. Khi đó a+b bằng

A.10+ √7

B.22

C. √7 + 15

D.Đáp án khác.

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

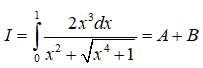
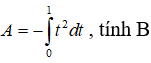
Câu 37: Cho . Đặt t = x² . Biết

Hiển thị đáp án

Đáp án: B

Giải thích:

Đặt t = x² ⇒ dt = 2xdx. Ta có:

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Câu 38: Nếu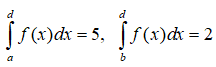với a < d < b thì

A.-2

B.3

C.8

D.0

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có:

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Câu 39: Cho tích phân 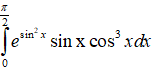. Nếu biến đổi số t = sin²x thì:

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Câu 40:

A. Không xác định được

B.1

C.3

D.-1

Hiển thị đáp án

Đáp án: D

Giải thích:

Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Các câu hỏi trắc nghiệm Toán lớp 12 có đáp án, chọn lọc khác:

Trắc nghiệm Ứng dụng tích phân có đáp án

Trắc nghiệm Ôn tập Chương 3 - Nguyên hàm - Tích phân và ứng dụng có đáp án

Trắc nghiệm Số phức có đáp án

Trắc nghiệm Cộng, trừ và nhân số phức có đáp án

Trắc nghiệm Phép chia số phức có đáp án

1 1,857 22/12/2023

Tải về

Trang trước

Trang sau

Xem thêm các chương trình khác:

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 3 lên lớp 4

Lớp 3 - Sách cũ

Tiếng Anh 3