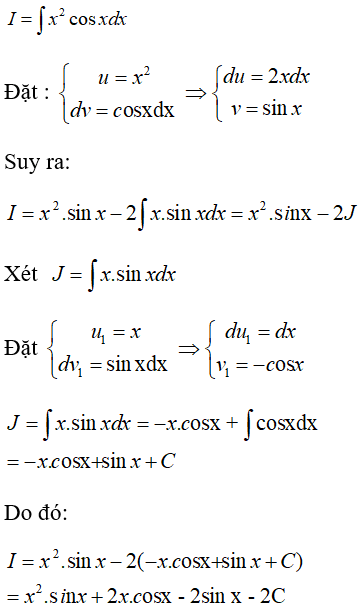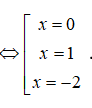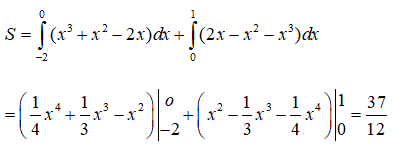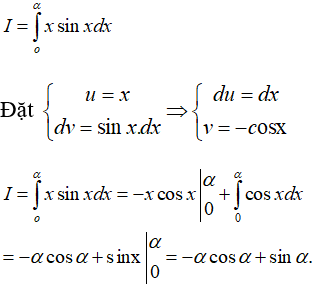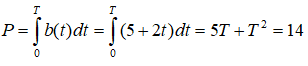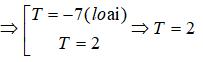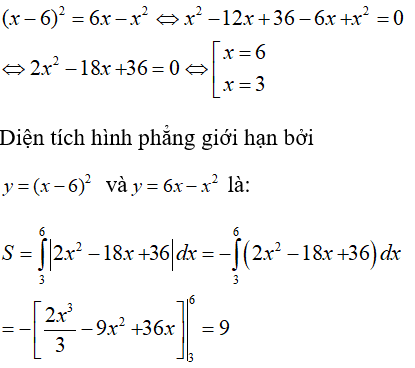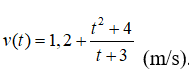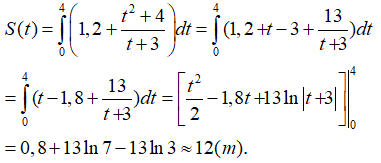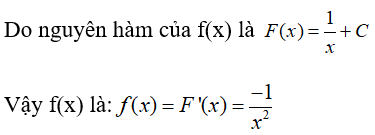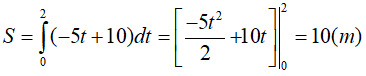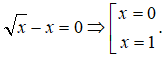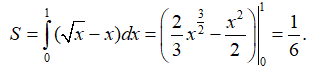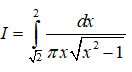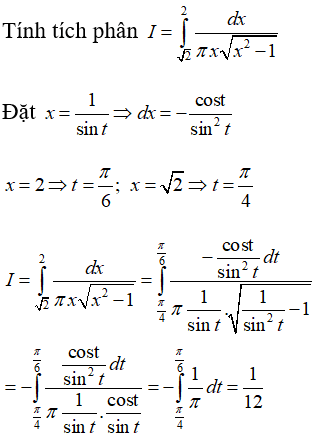TOP 40 câu Trắc nghiệm Ôn tập Chương 3 (có đáp án 2024) - Toán 12
Bộ 40 câu hỏi trắc nghiệm Toán lớp 12 Bài: Ôn tập Chương 3 - Nguyên hàm - Tích phân và ứng dụng có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 12 Bài Ôn tập chương 3.
Trắc nghiệm Toán 12 Bài: Ôn tập Chương 3 - Nguyên hàm - Tích phân và ứng dụng
Câu 1. Cho F(x) là một nguyên hàm của hàm số f(x)=sin2x1+cosx thỏa mãn F(π2)=0. Tính F(0).
A. F(0)=2ln2+2.
B. F(0)=2ln2.
C. F(0)=ln2.
D. F(0)=2ln2−2.
Đáp án: D
Giải thích:
f(x)=sin2x1+cosx
=2sinx.cosx1+cosx
Đặt u=1+cosx⇒du=−sinxdx và cosx=u − 1.
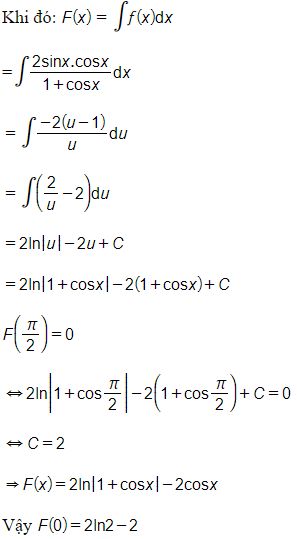
Câu 2. Tìm nguyên hàm của hàm số f(x)=(x+1).sin2x.
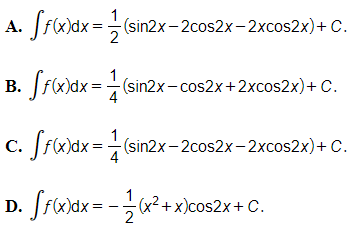
Đáp án: C
Giải thích:
Đặt {u=x+1dv=sin2xdx
⇒{du=dxv=−12cos2x
Khi đó:
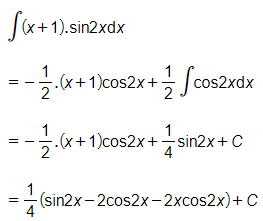
Câu 3. Cho hàm số f(x) có 9∫0f(x)dx=9. Tính 3∫0f(3x)dx.
A. 3∫0f(3x)dx=3.
B. 3∫0f(3x)dx=27.
C. 3∫0f(3x)dx=−3.
D. 3∫0f(3x)dx=1.
Đáp án: A
Giải thích:
Đặt t=3x ⇒dt=3dx
⇒dx=13dt.
Đổi cận x=0⇒t=0
x=3⇒t=9
⇒3∫0f(3x)dx=139∫0f(t)dt
=139∫0f(x)dx=3
Câu 4. Trong các khẳng định sau, khẳng định nào sai?
A. ∫dxx=lnx+C.
B. ∫xαdx=xα+1α+1+C , α≠−1.
C. ∫axdx=axlna+C.
D. ∫1cos2xdx=tanx+C.
Đáp án: A
Giải thích:
Ta có ∫dxx=ln|x|+C nên đáp án A sai.
Câu 5. Tính I=∫2x√x2+1dx bằng cách đặt u=√x2+1, mệnh đề nào dưới đây đúng?
A. I=2∫√udu.
B. I=∫udu.
C. I=∫u2du.
D. I=2∫u2du.
Đáp án: D
Giải thích:
Đặt u=√x2+1
⇒u2=x2+1
⇒2udu=2xdx.
⇒I=∫2u.u.du
=2∫u2du
Câu 6. Cho I=3∫0|x−2|dx. Khẳng định nào sau đây đúng?
A. I=|3∫0(x−2)dx|.
B. I=−2∫0(x−2)dx+3∫2(x−2)dx.
C. I=2∫0(x−2)dx+3∫2(x−2)dx.
D. I=2∫0(x−2)dx−3∫2(x−2)dx.
Đáp án: B
Giải thích:
Ta có: |x−2|={x−2, x≥2−(x−2), x<2
Suy ra: I=3∫0|x−2|dx
=−2∫0(x−2)dx+3∫2(x−2)dx.
Vậy I=−2∫0(x−2)dx+3∫2(x−2)dx
Câu 7. Hàm số F(x)=x33−cosx là một nguyên hàm của hàm số nào sau đây?
A. f(x)=3x2+cosx.
B. f(x)=x2+sinx.
C. f(x)=x2−sinx.
D. f(x)=x412+sinx.
Đáp án: B
Giải thích:
Hàm số F(x) là một nguyên hàm của hàm số f(x)
⇒F'
Ta có
Câu 8. Tìm ta được
A. .
B. .
C. .
D. .
Đáp án: A
Giải thích:
Ta có
Câu 9. Nguyên hàm của hàm số với là
A. .
B. .
C. .
D. .
Đáp án: A
Giải thích:
Ta có
Câu 10. Nguyên hàm của hàm số , là
A. .
B. .
C. .
D. .
Đáp án: D
Giải thích:
Ta có
Câu 11. Biết . Với là các số nguyên và tối giản. Trong các khẳng định sau khẳng định nào đúng?
A. .
B. .
C. .
D. .
Đáp án: C
Giải thích:
Đặt .
Đổi cận
Câu 12. Cho đồ thị hàm số như hình vẽ bên.
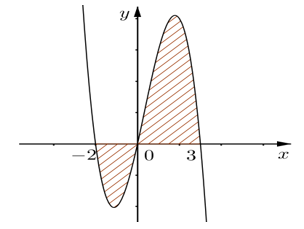
Diện tích S của hình phẳng phần tô đậm trong hình được tính theo công thức nào sau đây?
A. .
B. .
C. .
D. .
Đáp án: D
Giải thích:
Theo hình vẽ, ta có
.
Câu 13. Diện tích hình phẳng S giới hạn bởi các đồ thị hàm số và trục hoành Ox (như hình vẽ) được tính bởi công thức nào dưới đây?
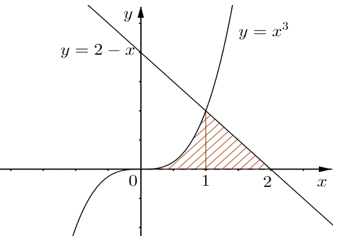
A. .
B. .
C. .
D. .
Đáp án: D
Giải thích:
Xét các phương trình hoành độ giao điểm
+)
+)
+)
Dựa vào hình vẽ, ta có
Câu 14. Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng và , biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x thì được thiết diện là một hình chữ nhật có hai cạnh là 3x và .
A. .
B. .
C. .
D. .
Đáp án: D
Giải thích:
Diện tích thiết diện (hình chữ nhật) là .
Suy ra thể tích cần tính
Câu 15. Tìm .
A.
B.
C.
D.
Đáp án: B
Giải thích:
Ta có:
Câu 16. Cho F(x) là một nguyên hàm của hàm số . Biết . Giá trị của là
A. .
B. 3.
C. .
D. .
Đáp án: D
Giải thích:
. Vậy
Do đó, .
Câu 17. Giả sử là hàm số liên tục trên khoảng K và a, b, c là ba số bất kỳ trên khoảng K. Khẳng định nào sau đây sai?
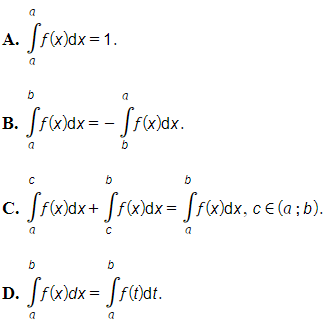
Đáp án: A
Giải thích:
Ta có:
Câu 18. Cho các số thực . Nếu hàm số là một nguyên hàm của hàm số thì
A. .
B. .
C. .
D. .
Đáp án: D
Giải thích:
Theo giả thiết là một nguyên hàm của hàm số nên ta có
Câu 19. Cho hàm số xác định và liên tục trên thỏa mãn . Giá trị bằng
A. .
B. .
C. .
D. .
Đáp án: B
Giải thích:
Theo đề
Xét . Đặt
Đổi cận:
| x |
0 |
1 |
| t |
0 |
1 |
Từ đó:
Câu 20. Cho hình phẳng D giới hạn bởi đường cong và trục hoành. Tính thể tích V của khối tròn xoay tạo thành khi quay D quanh trục hoành.
A. .
B. .
C. .
D. .
Đáp án: A
Giải thích:
Phương trình hoành độ giao điểm:
Thể tích cần tính là:
Câu 21. Để tính theo phương pháp nguyên hàm từng phần, ta đặt
A.
B.
C.
D.
Đáp án: A
Giải thích:
Đặt
Câu 22. Cho hàm số f(x) liên tục trên R, diện tích S của hình phẳng giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng được tính theo công thức
A. .
B. .
C. .
D. .
Đáp án: B
Giải thích:
Diện tích của hình phẳng giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng , , được tính theo công thức .
Câu 23. Cho hàm số liên tục trên . Gọi D là hình phẳng giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng , . Thể tích khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức
A. .
B. .
C. .
D. .
Đáp án: A
Giải thích:
Thể tích khối tròn xoay tạo thành khi quay D quanh trục hoành là:
Câu 24. Hàm số có một nguyên hàm là . Nếu thì bằng
A. .
B. .
C. .
D. .
Đáp án: A
Giải thích:
Đặt
.
Vì nên .
Vậy
.
Câu 25. Cho hàm số . Hàm số có đồ thị như hình vẽ bên.
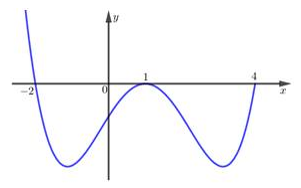
Biết rằng diện tích hình phẳng giới hạn bởi trục Ox và đồ thị hàm số trên đoạn và lần lượt bằng 9 và 12. Cho Giá trị của biểu thức bằng
A. 21
B. 9
C. 3
D. -3
Đáp án: C
Giải thích:
Từ đồ thị hàm số trên mỗi đoạn và
Diện tích hình phẳng giới hạn bởi trục Ox với đồ thị hàm số trên đoạn là:
Diện tích hình phẳng giới hạn bởi trục Ox với đồ thị hàm số trên đoạn [1;4] là
Vậy
Câu 26. Cho tích phân , giá trị của a + 2b bằng
A. 3.
B. .
C. .
D. 2.
Đáp án: D
Giải thích:
Đặt
Đổi cận
Ta có . Suy ra a = 1 và . Tính được a + 2b = 2.
Câu 27. Cho hàm số liên tục trên R và . Giá trị của biểu thức là
A. .
B. .
C. .
D. .
Đáp án: B
Giải thích:
Đặt .
Đổi cận
Ta có
Câu 28. Cho hàm số đa thức bậc ba có đồ thị như hình vẽ. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục hoành.
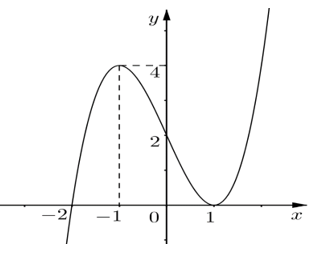
A. 6
B.
C.
D. 8
Đáp án: C
Giải thích:
Đồ thị hàm số cắt và tiếp xúc trục hoành lần lượt tại tại điểm (-2;0) và (1;0) nên hàm số có dạng
Mặt khác đồ thị hàm số lại đi qua điểm (-1;4) nên ta có .
Vậy .
Diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục hoành là:
Câu 29. Một công ty quảng cáo X muốn làm một bức tranh trang trí hình ở chính giữa của một bức tường hình chữ nhật ABCD có chiều cao , chiều dài (hình vẽ bên). Cho biết là hình chữ nhật có ; cung có hình dạng là một phần của cung parabol có đỉnh I là trung điểm của cạnh AB và đi qua hai điểm C, D. Kinh phí làm bức tranh là 900.000 đồng/. Hỏi công ty X cần bao nhiêu tiền để làm bức tranh đó?
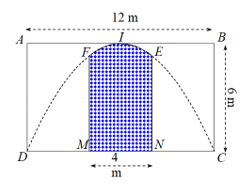
A. 20.400.000 đồng.
B. 20.600.000 đồng.
C. 20.800.000 đồng.
D. 21.200.000 đồng.
Đáp án: C
Giải thích:
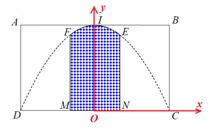
Gọi O là trung điểm MN. Chọn hệ trục tọa độ Oxy như hình vẽ.
Khi đó, ta có phương trình đường parabol đỉnh và đi qua hai điểm là
Diện tích bức tranh là diện tích hình phẳng giới hạn bởi đường parabol (P) trục Ox và hai đường thẳng . Khi đó
Vậy, số tiền công ty X cần dùng để làm bức tranh là
(đồng)
Câu 30. Một hoa văn trang trí được tạo ra từ một miếng bìa mỏng hình vuông cạnh bằng cm bằng cách khoét đi bốn phần bằng nhau có hình dạng parabol như hình bên. Biết cm, cm. Tính diện tích bề mặt hoa văn đó.
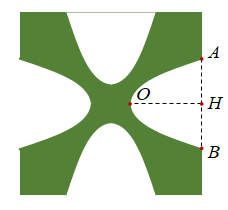
A.
B. .
C. .
D.
Đáp án: A
Giải thích:
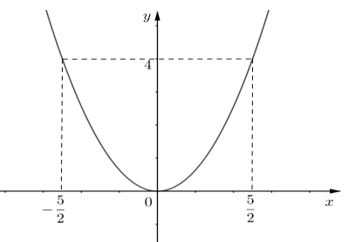
Chọn hệ trục tọa độ sao cho O là gốc tọa độ, OH thuộc Oy, Ox vuông góc với OH tại O chiều dương hướng từ A đến B. Khi đó ta có . Giả sử parabol (P) đi qua nhận O làm đỉnh có dạng:
Dễ dàng ta có hệ phương trình
Do đó: .
Gọi diện tích hình phẳng giới hạn các đường là
Khi đó ta có:
Do đó diện tích hình hoa văn là:
Câu 31.
A. I = x2.sinx + x.cosx - 2sinx + C
B. I = x2.sinx + 2x.cosx - 2sinx + C
C. I = x.sinx + 2x.cosx + C
D. I = 2x.cosx + sinx + C
Câu 32. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số và đồ thị hàm số
Câu 33. Tích phân 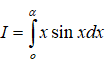
A. αcosα - sinα
B. αcosα + sinα
C. -αcosα + sinα
D. -αcosα - sinα
Đáp án: C
Giải thích:
Áp dụng công thức tích phân từng phần ta có:
Câu 34. Sau chiến tranh thế giới thứ hai, tốc độ sinh ở cả nước phương Tây tăng rất nhanh. Giả sử rằng tốc độ sinh được cho bởi: b(t) = 5 + 2t, 0 ≤ t ≤ 10 , ( ở đó t số năm tính từ khi chiến tranh kết thúc, b(t) tính theo đơn vị triệu người). Tìm khoảng thời gian T sao cho số lượng trẻ được sinh ra là 14 triệu kể từ khi kết thức chiến tranh.
Câu 35. Diện tích hình phẳng giới hạn bởi y = (x - 6)2 và y = 6x - x2 là:
A. 9
B. 9/2
C. 0
D. Kết quả khác.
Đáp án: A
Giải thích:
Phương trình hoành độ giao điểm:
Câu 36. Một vật chuyển động với vận tốc
Quãng đường vật đi được sau 4s xấp xỉ bằng:
A. 11m
B. 12m
C. 13m
D. 14m.
Câu 37. Biết nguyên hàm của f(x) là 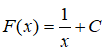
A. 1/x2
B. -1/x2
C. ln|x|
D. -ln|x|
Câu 38. Một ô tô đang chạy với vận tốc 10m/s thì người lái đạp phanh, từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc v(t) = -5t + 10(m/s), trong đó t là khoảng thời gian tính bằng giây , kể từ lúc bắt đầu đạp phanh .Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét?
A.0,2m
B.2m
C.10m
D.20m.
Câu 39. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục hoành.
Câu 40. Tính tích phân
A. π/12
B. π2/12
C. 1/12
D. Một đáp án khác
Đáp án: C
Giải thích:
Các câu hỏi trắc nghiệm Toán lớp 12 có đáp án, chọn lọc khác:
Trắc nghiệm Cộng, trừ và nhân số phức có đáp án
Trắc nghiệm Phép chia số phức có đáp án
Xem thêm các chương trình khác:
- Trắc nghiệm Sinh học lớp 7 có đáp án
- Trắc nghiệm Toán lớp 7 có đáp án
- Trắc nghiệm Ngữ văn lớp 7 có đáp án
- Trắc nghiệm Sinh học 8 có đáp án
- Trắc nghiệm Toán lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn 8 có đáp án
- Trắc nghiệm Hóa học lớp 8 có đáp án
- Trắc nghiệm Địa Lí lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Tiếng Anh lớp 8 có đáp án
- Trắc nghiệm GDCD lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Lịch sử lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Vật Lí lớp 8 có đáp án
- Trắc nghiệm Công nghệ lớp 8 có đáp án
- Trắc nghiệm Tin học lớp 8 có đáp án
- Trắc nghiệm Sinh học lớp 9 có đáp án
- Trắc nghiệm Toán lớp 9 có đáp án
- Trắc nghiệm Ngữ văn 9 có đáp án
- Trắc nghiệm Hóa học lớp 9 có đáp án
- Trắc nghiệm Địa lí lớp 9 có đáp án
- Trắc nghiệm Tiếng Anh lớp 9 có đáp án
- Trắc nghiệm GDCD lớp 9 có đáp án
- Trắc nghiệm Lịch sử lớp 9 có đáp án
- Trắc nghiệm Vật lí lớp 9 có đáp án
- Trắc nghiệm Công nghệ lớp 9 có đáp án
- Trắc nghiệm Sinh học lớp 10 có đáp án
- Trắc nghiệm Toán lớp 10 có đáp án
- Trắc nghiệm Hóa học lớp 10 có đáp án
- Trắc nghiệm Ngữ văn lớp 10 có đáp án
- Trắc nghiệm Vật Lí lớp 10 có đáp án
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án
- Trắc nghiệm Sinh học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Toán lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Hóa học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn lớp 11 có đáp án
- Trắc nghiệm Tiếng Anh lớp 11 có đáp án
- Trắc nghiệm Vật Lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Địa lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm GDCD lớp 11 có đáp án
- Trắc nghiệm Lịch sử lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Công nghệ lớp 11 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 11 có đáp án
- Trắc nghiệm Tin học lớp 11 có đáp án