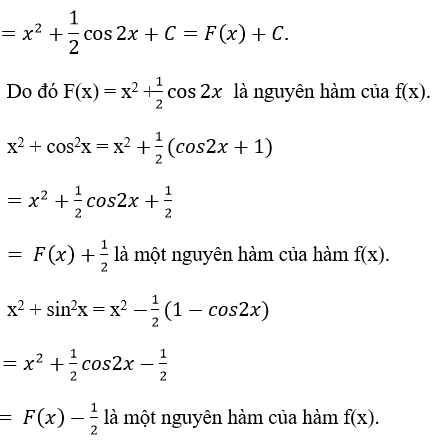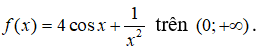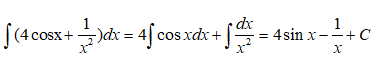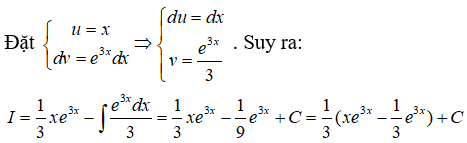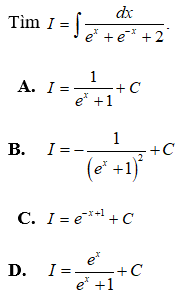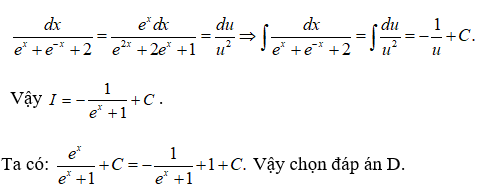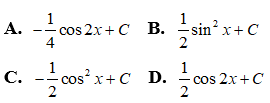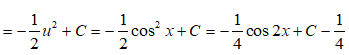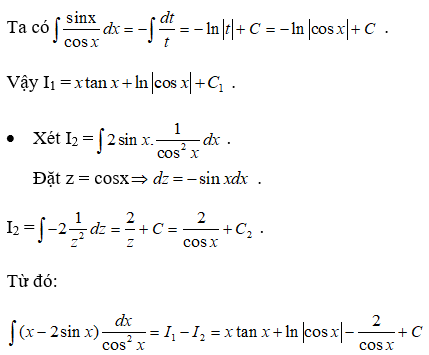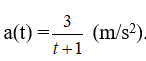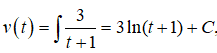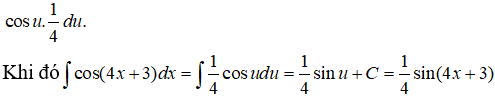Nội dung bài viết

    Xem thêm

    TOP 40 câu Trắc nghiệm Nguyên hàm (có đáp án 2024) - Toán 12

    Bộ 40 câu hỏi trắc nghiệm Toán lớp 12 Bài 1: Nguyên hàm có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 12 Bài 1.

    1 1,970 22/12/2023
    Tải về
    Trang trước
    Trang sau  

    Trắc nghiệm Toán 12 Bài 1: Nguyên hàm

    Bài giảng Trắc nghiệm Toán 12 Bài 1: Nguyên hàm

    Câu 1. Tính ∫dx√1−x thu được kết quả là:

    A. C√1−x

    B. −2√1−x+C

    C. 2√1−x+C

    D. √1−x+C

    Đáp án: B

    Giải thích:

    Ta có: ∫dx√1−x=−2√1−x+C

    Câu 2. Họ nguyên hàm của hàm số f(x)=x3√1−x2 là:

    A. 13(x2+2)√1−x2+C

    B. −13(x2+1)√1−x2+C

    C. 13(x2+1)√1−x2+C

    D. −13(x2+2)√1−x2+C

    Đáp án: D

    Giải thích:

    Ta có : I=∫x3√1−x2dx

    Đặt t=√1−x2

    ⇒t2=1−x2

    ⇒−tdt=xdx

    Khi đó: I=−∫(1−t2)ttdt

    =∫(t2−1)dt=t33−t+C

    Thay t=√1−x2 ta được I=(√1−x2)33−√1−x2+C

    =−13(x2+2)√1−x2+C

    Câu 3. Tính F(x)=∫dxx√2lnx+1

    A. F(x)=2√2lnx+1+C

    B. F(x)=√2lnx+1+C

    C. F(x)=14√2lnx+1+C

    D. F(x)=12√2lnx+1+C

    Đáp án: B

    Giải thích:

    Ta có: F(x)=∫d(√2lnx+1)=√2lnx+1+C

    Câu 4. Nguyên hàm của hàm số f(x) = x2– 3x + 1x   là

    A. x44−3x22−ln|x|+C

    B. x33−3x22+lnx+C

    C. x44−3x22+ln|x|+C

    D. x33+3x22+lnx+C

    Đáp án: C

    Giải thích:

    Ta có: ∫(x3−3x+1x)dx

    =x44−3x22+ln|x|+C

    Câu 5. Nguyên hàm của hàm số y=√3x−1 trên (13;+∞) là:

    A. √32x2−x+C

    B. 29√(3x−1)3+C

    C. √32x2−x+C

    D. 19√(3x−1)3+C

    Đáp án: B

    Giải thích:

    Ta có: ∫√3x−1.dx

    =13.21+2√(3x−1)3+C

    =29√(3x−1)3+C

    Câu 6. Tính F(x)=∫x3x4−1dx

    A. F(x)=ln|x4−1|+C

    B. F(x)=14ln|x4−1|+C

    C. F(x)=12ln|x4−1|+C

    D. F(x)=13ln|x4−1|+C

    Đáp án: B

    Giải thích:

    Ta có: ∫x3x4−1dx

    =14∫d(x4−1)x4−1

    =14ln|x4−1|+C

    Câu 7. Một nguyên hàm của hàm số y=sin3x 

    A. −13cos3x 

    B. −3cos3x 

    C. 3cos3x  

    D. 13cos3x 

    Đáp án: A

    Giải thích:

    Ta có:

    ∫sin3xdx=−13cos3x+C

    Câu 8. Cho hàm số f(x)=5+2x4x2 . Khi đó:

    A. ∫f(x)dx=2x33−5x+C

    B. ∫f(x)dx=2x3−5x+C

    C. ∫f(x)dx=2x33+5x+C

    D. ∫f(x)dx=2x33+5lnx2+C

    Đáp án: A

    Giải thích:

    Ta có: ∫5+2x4x2dx

    =∫(5x2+2x2)dx

    =2x33−5x+C

    Câu 9. Một nguyên hàm của hàm số: f(x)=x√1+x2 là:

    A. F(x)=13(√1+x2)3

    B. F(x)=13(√1+x2)2

    C. F(x)=x22(√1+x2)2

    D. F(x)=12(√1+x2)2

    Đáp án: A

    Giải thích:

    Ta có : I=∫x√1+x2dx

    Đặt t=√1+x2

    ⇒t2=1+x2

    ⇒tdt=xdx

    Khi đó: I=∫t.tdt=t33+C

    Thay t=√1+x2 ta được I=(√1+x2)33+C

    Câu 10. Họ các nguyên hàm của hàm số y=sin2x là:

    A. −cos2x+C

    B. −12cos2x+C

    C. cos2x+C

    D. 12cos2x+C

    Đáp án: B

    Giải thích:

    Ta có: ∫sin2xdx=−12cos2x+C

    Câu 11. Tìm nguyên hàm của hàm số f(x) thỏa mãn điều kiện: f(x)=2x−3cosx, F(π2)=3

    A. F(x)=x2−3sinx+6+π24

    B. F(x)=x2−3sinx−π24

    C. F(x)=x2−3sinx+π24

    D. F(x)=x2−3sinx+6−π24

    Đáp án: D

    Giải thích:

    Ta có: F(x)=∫(2x−3cosx)dx

    =x2−3sinx+C

    F(π2)=3

    ⇔(π2)2−3sinπ2+C=3

    ⇔C=6−π24

    Vậy F(x)=x2−3sinx+6−π24

    Câu 12. Một nguyên hàm F(x) của hàm số f(x)=2x+1sin2x thỏa mãn F(π4)=−1 là:

    A. F(x)=−cotx+x2−π216

    B. F(x)=cotx−x2+π216

    C. F(x)=−cotx+x2

    D. F(x)=−cotx+x2−π216

    Đáp án: A

    Giải thích:

    Ta có: F(x)=∫(2x+1sin2x)dx

    =x2−cotx+ C

    F(π4)=−1

    ⇔(π4)2−cotπ4+C=−1

    ⇔C=π216

    Vậy F(x)=−cotx+x2−π216

    Câu 13. Cho hàm số f(x)=cos3x.cosx. Một nguyên hàm của hàm số f(x) bằng 0 khi x=0 là:

    A. 3sin3x+sinx

    B. sin4x8+sin2x4

    C. sin4x2+sin2x4

    D. cos4x8+cos2x4

    Đáp án: D

    Giải thích:

    Ta có: F(x)=∫cos3x.cos.dx

    =12∫(cos2x+cos4x)dx

    =18sin4x+14sin2x+C

    Vậy F(x)=cos4x8+cos2x4

    Câu 14: Nguyên hàm ∫[sin2(3x+1)+cosx]dx là:

    A. 12x−3sin(6x+2)+sinx+C.

    B. x−3sin(6x+2)+sinx+C.

    C. 12x−3sin(3x+1)+sinx+C.

    D. 12x−3sin(6x+2)−sinx+C.

    Đáp án: A

    Giải thích:

    Ta có:

    ∫[sin2(3x+1)+cosx]dx

    =∫[1−cos(6x+2)2+cosx]dx

    =∫[12−12cos(6x+2)+cosx]dx

    =12x−3sin(6x+2)+sinx+C

    Câu 15: Gọi F(x) là nguyên hàm của hàm số f(x)=√x+1−1x2. Nguyên hàm của f(x) biết F(3)=6 là:

    A. F(x)=23√(x+1)3−1x+13.

    B. F(x)=23√(x+1)3+1x+13.

    C. F(x)=23√(x+1)3−1x−13.

    D. F(x)=23√(x+1)3+1x−13.

    Đáp án: B

    Giải thích:

    Ta có: ∫(√x+1−1x2)dx

    =23√(x+1)3+1x+C

    Theo đề bài, ta lại có: F(3)=6

    ⇔23√(3+1)3+13+C=6

    ⇔C=13

    F(x)=23√(x+1)3+1x+13

    Câu 16: Gọi F(x) là nguyên hàm của hàm số f(x)=4x3+2(m−1)x+m+5, với m là tham số thực. Một nguyên hàm của f(x) biết rằng F(1)=8 và F(0)=1 là:

    A. F(x)=x4+2x2+6x+1

    B. F(x)=x4+6x+1.

    C. F(x)=x4+2x2+1.

    D. Đáp án A và B.

    Đáp án: B

    Giải thích:

    Ta có:

    ∫[4x3+2(m−1)x+m+5]dx

    =x4+(m−1)x2+(m+5)x+C

    Lại có:

    {F(0)=1F(1)=8

    ⇔{C=11+m−1+m+5+C=8

    ⇔{C=1m=1

    Vậy F(x)=x4+6x+1.

    Câu 17: Nguyên hàm của ∫xx2+1dx là:

    A. ln|t|+C, với t=x2+1

    B. −ln|t|+C, với t=x2+1

    C. 12ln|t|+C, với t=x2+1.

    D. −12ln|t|+C, với t=x2+1

    Đáp án: C

    Giải thích:

    Đặt t=x2+1⇒dt=2xdx

    ⇒∫xx2+1dx=...

    =12∫1tdt=12ln|t|+C

    Câu 18: Kết quả nào dưới đây không phải là nguyên hàm của ∫(sin3x+cos3x)dx?

    A. 3cosx.sin2x−3sinx.cos2x+C.

    B. 32sin2x(sinx−cosx)+C.

    C. 3√2sin2xsin(x−π4)+C.

    D. 3√2sinx.cosx.sin(x−π4)+C.

    Đáp án: C

    Giải thích:

    Ta có:

    ∫(sin3x+cos3x)dx

    =3cosx.sin2x−3sinx.cos2x+C

    =32sin2x(sinx−cosx)+C

    =3√22sin2xsin(x−π4)+C

    Câu 19: Với phương pháp đổi biến số (x→t) , nguyên hàm ∫ln2xxdx bằng:

    A. 12t2+C.

    B. t2+C.

    C. 2t2+C.

    D. 4t2+C.

    Đáp án: A

    Giải thích:

    Đặt t=ln2x⇒dt=2.12xdx

    ⇒dt=1xdx

    ⇒∫ln2xxdx=...

    =∫tdt=12t2+C

    Câu 20: Với phương pháp đổi biến số (x→t), nguyên hàm ∫1x2+1dx bằng:

    A. 12t2+C.

    B. 12t+C.

    C. t2+C.

    D. t+C.

    Đáp án: D

    Giải thích:

    Ta đặt : x=tant,t∈(−π2;π2)

    ⇒dx=1cos2tdt

    ⇒∫1x2+1dx=...

    =∫dt=t+C

    Câu 21: Với phương pháp đổi biến số (x→t), nguyên hàm I=∫1√−x2+2x+3dx bằng:

    A. sint+C.

    B. −t+C.

    C. −cost+C.

    D. t+C.

    Đáp án: D

    Giải thích:

    Ta biến đổi: I=∫1√4−(x−1)2dx.

    Đặt x−1=2sint,t∈[−π2,π2]

    ⇒dx=2costdt

    ⇒I=∫dt=t+C

    Câu 22: Tìm I=∫ex(3x−2)+√x−1√x−1(ex.√x−1+1)dx?

    A. I=x+ln(ex.√x−1+1)+C.

    B. I=x−ln(ex.√x−1+1)+C.

    C. I=ln(ex.√x−1+1)+C.

    D. I=ln(ex.√x−1−1)+C.

    Đáp án: A

    Giải thích:

    I=∫ex(3x−2)+√x−1√x−1(ex.√x−1+1)dx

    =∫√x−1(ex.√x−1+1)+ex(2x−1)√x−1(ex.√x−1+1)dx

    Đặt : t=ex.√x−1+1

    ⇒dt=(ex2√x−1+ex√x−1)dx

    =ex(2x−1)2√x−1dx

    Vậy ⇒I=∫dx+∫ex(2x−1)√x−1(ex√x−1+1)dx

    =x+∫1tdt=x+ln|t|+C

    =x+ln(ex.√x−1+1)+C

    Câu 23: Tìm J=∫ex.sinxdx?

    A. J=ex2(cosx−sinx)+C.

    B. J=ex2(sinx+cosx)+C.

    C. J=ex2(sinx−cosx)+C.

    D. J=ex2(sinx+cosx+1)+C.

    Đáp án: C

    Giải thích:

    Đặt : {u1=exdv1=sinx.dx

    ⇒{du1=ex.dxv1=−cosx

    ⇒J=−excosx+∫excosxdx

    =−excosx+T         (T=∫ex.cosxdx)

    Tính T=∫ex.cosxdx :

    Đặt : {u2=exdv2=cosx.dx

    ⇒{du2=ex.dxv2=sinx

    Câu 24: Tìm nguyên hàm của hàm số f(x)=x3ln(4−x24+x2)?

    A. x4ln(4−x24+x2)−2x2.

    B. (x4−164)ln(4−x24+x2)−2x2.

    C. x4ln(4−x24+x2)+2x2

    D. (x4−164)ln(4−x24+x2)+2x2.

    Đáp án: B

    Giải thích:

    Đặt : {u=ln(4−x24+x2)dv=x3dx

    ⇒{du=16xx4−16v=x44−4=x4−164

    ⇒∫x4ln(4−x24+x2)dx

    =(x4−164)ln(4−x24+x2)−∫4xdx

    =(x4−164)ln(4−x24+x2)−2x2+C

    Câu 25: Tìm I=∫sinxsinx+cosxdx?

    A. I=12(x+ln|sinx+cosx|)+C.

    B. I=x+ln|sinx+cosx|+C

    C. I=x−ln|sinx+cosx|+C.

    D. I=12(x−ln|sinx+cosx|)+C.

    Đáp án: D

    Giải thích:

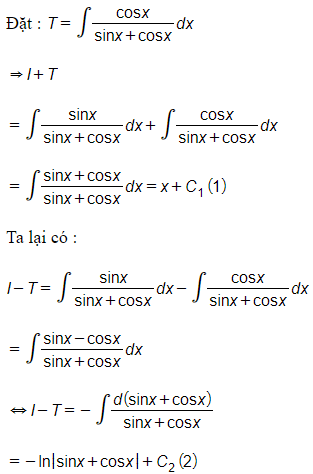
    Trắc nghiệm Nguyên hàm có đáp án - Toán lớp 12 (ảnh 1)

    Từ (1);(2) ta có hệ: {I+T=x+C1I−T=−ln|sinx+cosx|+C2

    ⇒{I=12(x−ln|sinx+cosx|)+CT=12(x+ln|sinx+cosx|)+C

    Câu 26: Tìm Q=∫√x−1x+1dx?

    A. Q=√x2−1+ln|x+√x2−1|+C.

    B. Q=√x2−1−ln|x+√x2−1|+C.

    C. Q=ln|x+√x2−1|−√x2−1+C.

    D. Cả đáp án B,C đều đúng.

    Đáp án: D

    Giải thích:

    Điều kiện :

    x−1x+1≥0⇔[x≥1x<−1

    Trường hợp 1 : Nếu x≥1 thì

    Q=∫√x−1x+1dx

    =∫x−1√x2−1dx

    =∫x√x2−1dx−∫1√x2−1dx

    =√x2−1−ln|x+√x2−1|+C

    Trường hợp 2: Nếu x<−1 thì

    Q=∫√x−1x+1dx

    =∫1−x√x2−1dx

    =∫1√x2−1dx−∫x√x2−1dx

    =ln|x+√x2−1|−√x2−1+C

    Câu 27: Tìm T=∫xn1+x+x22!+x33!+...+xnn!dx?

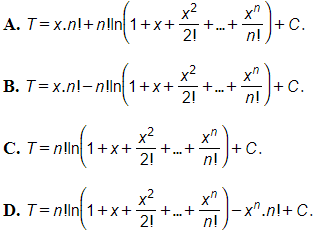
    Trắc nghiệm Nguyên hàm có đáp án - Toán lớp 12 (ảnh 1)

    Đáp án: D

    Giải thích:

    Điều kiện :

    x−1x+1≥0⇔[x≥1x<−1

    Trường hợp 1 : Nếu x≥1 thì

    Q=∫√x−1x+1dx

    =∫x−1√x2−1dx

    =∫x√x2−1dx−∫1√x2−1dx

    =√x2−1−ln|x+√x2−1|+C

    Trường hợp 2: Nếu x<−1 thì

    Q=∫√x−1x+1dx

    =∫1−x√x2−1dx

    =∫1√x2−1dx−∫x√x2−1dx

    =ln|x+√x2−1|−√x2−1+C

    Câu 28: Tìm T=∫dxn√(xn+1)n+1?

    A. T=(1xn+1)−1n+C

    B. T=(1xn+1)1n+C

    C. T=(xn+1)−1n+C

    D. T=(xn+1)1n+C.

    Đáp án: A

    Giải thích:

    Ta có :

    T=∫dxn√(xn+1)n+1

    =∫dxxn+1.n√(1xn+1)n+1

    =∫x−n−1(1xn+1)1+1ndx

    =∫x−n−1(1xn+1)−1−1ndx

    Đặt: t=1xn+1

    ⇒dt=−nxn+1=−nx−n−1

    ⇒T=−1n∫t−1−1ndt

    =t−1n+C

    =(1xn+1)−1n+C

    Câu 29: Tìm H=∫x2dx(xsinx+cosx)2?

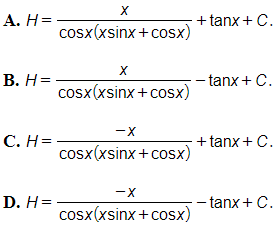
    Trắc nghiệm Nguyên hàm có đáp án - Toán lớp 12 (ảnh 1)

    Đáp án: C

    Giải thích:

    Ta có : H=∫x2(xsinx+cosx)2dx

    =∫xcosx(xsinx+cosx)2.xcosxdx

    Đặt

    {u=xcosxdv=xcosx(xsinx+cosx)2dx=d(xsinx+cosx)(xsinx+cosx)2

    ⇒{du=xsinx+cosxcos2xdxv=−1xsinx+cosx

    ⇒H=−xcosx.1xsinx+cosx+∫1cos2xdx

    =−xcosx(xsinx+cosx)+tanx+C

    Câu 30: Tìm R=∫1x2√2−x2+x dx?

    A. R=−tan2t2+14ln|1+sin2t1−sin2t|+C với t=12arctan(x2).

    B. R=−tan2t2−14ln|1+sin2t1−sin2t|+C với t=12arctan(x2).

    C. R=tan2t2+14ln|1+sin2t1−sin2t|+C với t=12arctan(x2).

    D. R=tan2t2−14ln|1+sin2t1−sin2t|+C với t=12arctan(x2).

    Đáp án: A

    Giải thích:

    Đặt x=2cos2t  với t∈(0;π2)

    Ta có : dx=−4sin2t.dt

    √2−x2+x=√2−2sin2t2+2cos2t

    =√4sin2t4cos2t=sintcost

    ⇒R=−∫14cos22t.sintcost.4sin2t.dt

    =−∫2sin2tcos22tdt

    =−∫1−cos2tcos22tdt

    ⇔R=−∫1cos22tdt+∫1cos2tdt

    =−tan2t2+14ln|1+sin2t1−sin2t|+C

    Câu 31: Trong các mệnh đề sau mệnh đề nào nhận giá trị đúng?

    A. Hàm số y = 1/x có nguyên hàm trên (-∞; +∞).

    B. 3x2 là một số nguyên hàm của x3 trên (-∞; +∞).

    C. Hàm số y = |x| có nguyên hàm trên (-∞;+∞).

    D. 1/x + C là họ nguyên hàm của ln⁡x trên (0;+∞).

    Đáp án: C

    Giải thích:

    Dựa vào định lí: Mọi hàm số liên tục trên K đều có nguyên

    hàm trên K. Vì y = |x| liên tục trên R nên có nguyên hàm trên R .

    Phương án A sai vì y=1/x không xác định tại x=0 ∈ (-∞;+∞).

    Phương án B sai vì 3x2 là đạo hàm của x3.

    Phương án D sai vì 1/x là đạo hàm của ln⁡x trên (0; +∞).

    Vậy chọn đáp án C.

    Câu 32: Hàm số nào dưới đây không phải là một nguyên hàm của f(x)=2x-sin⁡2x ?

    A. x2 + (1/2).cos⁡2x

    B. x2 + cos2 x

    C. x2 - sin2x

    D. x2 + cos⁡2x .

    Đáp án: D

    Giải thích:

    Ta có

    ∫(2x-sin⁡2x)dx=2∫xdx-∫sin⁡2xdx

    Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

    D không phải là nguyên hàm của f(x). Vậy chọn đáp án D.

    Câu 33: Tìm nguyên hàm của Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

    Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

    Đáp án: C

    Giải thích:

    Với x ∈ (0; +∞) ta cóBài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

    Vậy chọn đáp án C.

    Câu 34: Tìm I = ∫x.e3xdx

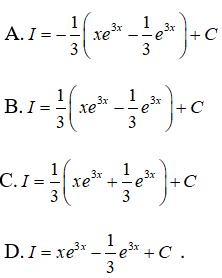
    Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

    Đáp án: B

    Giải thích:

    Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

    Câu 35:

    Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

    Đáp án: D

    Giải thích:

    Đặt u = ex + 1 ⇒ u' = ex. Ta có

    Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

    Câu 36: Trong các hàm số sau hàm số nào không phải là một nguyên hàm của f(x) = cosxsinx

    Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

    Đáp án: D

    Giải thích:

    Sử dụng phương pháp biến đổi số ta có:

    Đặt u = cosx thì u’ = -sinx và ∫sinxcosxdx = -∫u.u'dx = -∫udu

    Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

    Vậy chọn đáp án D.

    Câu 37: Tìm I=∫(3x2- x + 1)exdx

    A. I = (3x2 - 7x +8)ex + C

    B. I = (3x2 - 7x)ex + C

    C. I = (3x2 - 7x +8) + ex + C

    D. I = (3x2 - 7x + 3)ex + C

    Đáp án: A

    Giải thích:

    Sử dụng phương pháp tính nguyên hàm từng phần ta có:

    Đặt u = 3x2 - x + 1 và dv = exdx ta có du = (6x - 1)dx và v = ex . Do đó:

    ∫(3x2 - x + 1)exdx = (3x2 - x + 1)ex - ∫(6x - 1)exdx

    Đặt u1 = 6x - 1; dv1 = exdx Ta có: du1 = 6dx và v1 = ex .

    Do đó ∫(6x - 1)exdx = (6x - 1)ex - 6∫exdx = (6x - 1)ex - 6ex + C

    Từ đó suy ra

    ∫(3x2 - x + 1)exdx = (3x2 - x + 1)ex - (6x - 7)ex + C = (3x2 - 7x + 8)ex + C

    Vậy chọn đáp án A.

    Câu 38:

    Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

    Đáp án: C

    Giải thích:

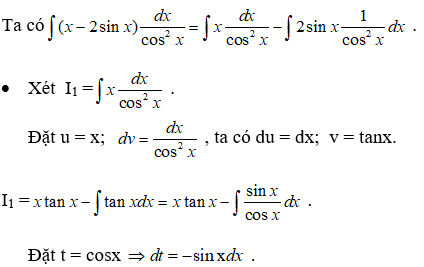
    Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12 Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

    Câu 39: Một vật chuyển động với vận tốc v(t) (m/s) có gia tốc

    Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

    Vận tốc ban đầu của vật là 6m/s. Vận tốc của vật sau 10 giây xấp xỉ bằng

    A. 10m/s

    B. 11m/s

    C. 12m/s

    D. 13m/s.

    Đáp án: D

    Giải thích:

    Vận tốc của vật bằng

    Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

    với t = 0 ta có v(0)= C = 6 nên phương trình vận tốc của chuyển động là :

    v(t) = 3ln(t + 1) + 6 (m/s)

    khi đó v(10) = 3ln11 + 6 ≈ 13 (m/s) .

    Câu 40: Tìm I = ∫cos(4x + 3)dx .

    A. I = sin(4x + 2) + C

    B. I = - sin(4x + 3) + C

    C. I = (1/4).sin(4x + 3) + C

    D. I = 4sin(4x + 3) + C

    Đáp án: C

    Giải thích:

    Đặt u = 4x + 3

    ⇒ du = 4dx ⇒ dx = 1/4 du và cos(4x+3)dx được viết thành

    Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

    Các câu hỏi trắc nghiệm Toán lớp 12 có đáp án, chọn lọc khác:

    Trắc nghiệm Tích phân có đáp án

    Trắc nghiệm Ứng dụng tích phân có đáp án

    Trắc nghiệm Ôn tập Chương 3 - Nguyên hàm - Tích phân và ứng dụng có đáp án

    Trắc nghiệm Số phức có đáp án

    Trắc nghiệm Cộng, trừ và nhân số phức có đáp án

    Tham khảo các loạt bài Trắc nghiệm lớp 12 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,970 22/12/2023
    Tải về
    Trang trước
    Trang sau  

    Xem thêm các chương trình khác: