TOP 40 câu Trắc nghiệm Mặt cầu (có đáp án 2024) - Toán 12
Bộ 40 câu hỏi nghiệm Toán lớp 12 Bài 2: Mặt cầu có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 12 Bài 2.
Trắc nghiệm Toán 12 Bài 2: Mặt cầu
Bài giảng Trắc nghiệm Toán 12 Bài 2: Mặt cầu
Câu 1: Cho hình chóp S.ABCD có đáy ABC là tam giác vuông tại B và SA⊥(ABC). Điểm nào sau đây là tâm của mặt cầu qua các điểm S,A,B,C?
A. Trung điểm của AC.
B. Trung điểm của AB.
C. Trung điểm của BC.
D. Trung điểm của SC.
Đáp án: D
Giải thích:
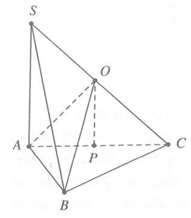
Gọi P là tâm đường tròn ngoại tiếp ΔABC. Trục đường tròn ngoại tiếp ΔABC cắt SC tại O.
Ta có {OA=OB=OCOC=OS
⇒OA=OB=OC=OS.
Vậy O là tâm mặt cầu qua các điểm S, A, B, C.
Câu 2: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và SA⊥(ABC). Gọi I và J lần lượt là hình chiếu vuông góc của A trên SB và SC. Điểm nào sau đây là tâm của mặt cầu qua năm điểm A, B, C, I, J?
A. Trung điểm của AC.
B. Trung điểm của BC.
C. Trung điểm của IJ.
D. Trọng tâm của ΔABC.
Đáp án: A
Giải thích:
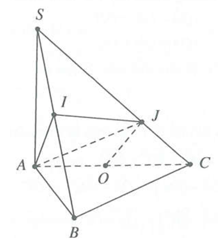
Gọi O là trung điểm của AC.
Ta có:
{AB⊥BC⇒OA=OC=OBAJ=JC⇒OA=OC=OJ
Từ {BC⊥ABBC⊥SA
⇒BC⊥(SAB)⇔BC⊥AI.
Mà AI⊥SB
⇒AI⊥(SBC)⇒AI⊥IC
⇒OA=OC=OI
⇒OA=OB=OC=OI=OJ.
Vậy O là tâm mặt cầu cần tìm.
Câu 3: Cho hình chóp có đáy ABCD là hình vuông và SA⊥(ABCD). Gọi I, J, K lần lượt là hình chiếu vuông góc của A trên SB, SC, SD. Điểm nào sau đây là tâm của mặt cầu qua bảy điểm A, B, C, D, I, J, K?
A. Tâm của ABCD.
B. Trung điểm của SB.
C. Trung điểm của SC.
D. Trung điểm của SD.
Đáp án: A
Giải thích:
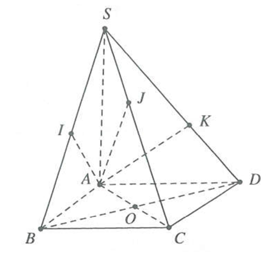
Gọi O là tâm của hình vuông ABCD.
Ta có {BC⊥ABBC⊥SA
⇒BC⊥(SAB)⇒BC⊥AI.
AI⊥SB⇒AI⊥(SBC)
⇒AI⊥IC⇒OA=OC=OI.
Tương tự OA=OC=OK.
Mà AJ⊥SC⇒OA=OC=OJ
⇒OA=OB=OC
=OD=OI=OJ=OK
⇒O là tâm mặt cầu cần tìm.
Câu 4: Cho tứ diện DABC, đáy ABC là tam giác vuông tại D, DA vuông góc với mặt đáy. Biết AB=3a,BC=4a,AD=5a. Bán kính mặt cầu ngoại tiếp hình chóp DABC có bán kính bằng
A. 5a√22.
B. 5a√23.
C. 5a√33.
D. 5a√32.
Đáp án: A
Giải thích:
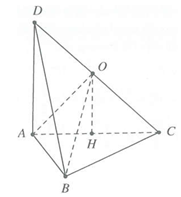
Gọi O là trung điểm của CD.
Ta có OA=OB=OC=OD
=R=12CD.
Cạnh CD=√AD2+AC2
=√AD2+AB2+BC2
=5a√2
R=5a√2.
Câu 5: Cho hình chóp tam giác có các cạnh vuông góc với nhau từng đôi một và SA=a,SB=b,SC=c. Mặt cầu ngoại tiếp hình chóp có bán kính là:
A. 12√a2+b2+c2.
B. 13√a2+b2+c2.
C. 32√a2+b2+c2.
D. 23√a2+b2+c2.
Đáp án: A
Giải thích:
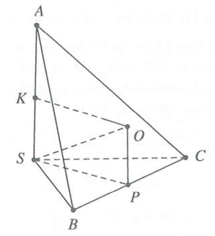
Ta có {SA⊥SBSA⊥SC⇒SA⊥(SBC).
Kí hiệu các điểm như hình vẽ với OP là trục đường tròn ngoại tiếp tam giác SBC và OK là trung trực của SA thì O là tâm mặt cầu.
Ta có R=OS=√OP2+SP2.
OP=SK=SA2=a2;
SP=12BC=12√b2+c2
R=12√a2+b2+c2.
Câu 6: Cho hình chóp tam giác S.ABC có các cạnh SA,SB,SC vuông góc với nhau từng đôi một và SA=SB=2a,SC=4a. Mặt cầu ngoại tiếp hình chóp có bán kính tính theo a là:
A. a√62.
B. a√3.
C. a√63.
D. a√6.
Đáp án: D
Giải thích:
Ta có {SA⊥SBSA⊥SC⇒SA⊥(SBC).
Kí hiệu các điểm như hình vẽ với OP là trục đường tròn ngoại tiếp tam giác SBC và OK là trung trực của SA thì O là tâm mặt cầu.
Ta có R=OS=√OP2+SP2.
OP=SK=SA2=a;
SP=12BC
=12√SB2+SC2
=a√5
R=a√6.
Câu 7: Cho hình chóp tam giác S.ABC, đáy là tam giác vuông tại A AB=3,AC=4, SA vuông góc với đáy, SA=2√14. Thể tích V của khối cầu ngoại tiếp hình chóp S.ABC là
A. V=169π6.
B. V=2197π8.
C. V=729π6.
D. V=13π8.
Đáp án: C
Giải thích:
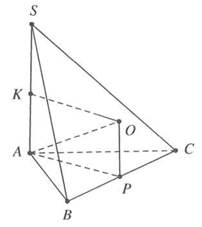
Kí hiệu các điểm như hình vẽ với OP là trục đường tròn ngoại tiếp tam giác ABC và OK là trung trực của SA thì O là tâm mặt cầu.
Ta có R=OA=√OP2+AP2
OP=AK=SA2=√14;
AP=12BC
=12√32+42=52
⇒R=92
⇒V=43πR3=2432π.
Câu 8: Cho hình chóp có đáy ABCD là hình vuông cạnh 2a. Mặt bên SAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính bán kính r của mặt cầu ngoại tiếp hình chóp .
A. r=a√22
B. r=3a2
C. r = a
D. r=a√2
Đáp án: D
Giải thích:
Đặt R1=RABCD;
R2=RSAB,
AB=(SAB)∩(ABC)
Tam giác ABDC là hình vuông cạnh bằng 2a nên
R1=AC2=2a√22=a√2.
Tam giác SAB vuông cân tại S nên
R2=AB2=a.
Do (SAB)⊥(ABC)
nên r=RS.ABC
=√R21+R22−AB24=a√2.
Câu 9: Cho hình chóp S.ABCD có SA⊥(ABCD), đáy ABCD là hình chữ nhật, AB=a,AD=2a, góc giữa đường thẳng SC và đáy bằng 450. Tính theo a thể tích của khối cầu ngoại tiếp hình chóp S.ABCD.
A. V=πa3√6.
B. V=10πa33.
C. V=5πa36.
D. V=5√10πa33.
Đáp án: D
Giải thích:
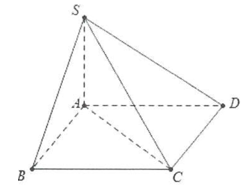
Do SA⊥(ABCD)
⇒(^SC;(ABCD))=^SCA=450.
Ta có:
AC=√AB2+AD2=a√5
⇒SA=ACtan450=a√5.
Lại có: Rd=RABCD=AC2=a√52.
Do SA⊥(ABCD)
⇒R=√SA24+R2d
=a√102.
Thể tích khối cầu ngoại tiếp hình chóp S.ABCD là:
V=43πR3=5√10πa33.
Câu 10: Cho tứ diện SABC có tam giác ABC vuông tại B, AB=a,BC=a√3,SA=a√2 và SB=a√2,SC=a√5. Tính bán kính mặt cầu ngoại tiếp tứ diện S.ABC.
A. R=a√2597.
B. R=a√2594.
C. R=a√2592.
D. R=a√3714.
Đáp án: B
Giải thích:
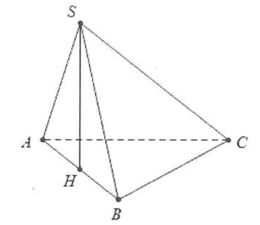
Gọi H là trung điểm của AB.
Do SA=SB⇒SH⊥AB.
Ta có: SB2+BC2=SC2=5a2
⇒SB⊥BC
Mặt khác: AB⊥BC
⇒BC⊥(SAB)⇒BC⊥SH
Suy ra SH⊥(ABC),
đặt R1=RABC=AC2=a.
Đặt R2=RSAB=SA.SB.AB4SSAB
=SA.SB.AB2.SH.AB=SA.SB2SH
=a2SH
Trong đó:
SH=√SB2−HB2
=a√72
⇒R2=2a√7
Suy ra:
RS.ABC=√R21+R22−AB24
=a√25914.
Câu 11: Cho ba điểm A, B, C cùng thuộc một mặt cầu và biết rằng ^ABC=900. Trong các khẳng định sau khẳng định nào đúng?
A. AB là một đường kính của mặt cầu đã cho
B. Luôn luôn có một đường tròn thuộc mặt cầu ngoại tiếp tam giác ABC
C. ABC là một tam giác vuông cân tại C
D. AB là đường kính của một đường tròn lớn trên mặt cầu đã cho
Đáp án: D
Câu 12: Trong các đa diện sau đây, đa diện nào không luôn luôn nội tiếp được trong mặt cầu:
A. Hình chóp tam giác (tứ diện)
B. Hình chóp ngũ giác đều
C. Hình chóp tứ giác
D. Hình hộp chữ nhật
Đáp án: C
Giải thích:
Chọn C vì cạnh bên đồng phẳng với trục và đáy là tứ giác nội tiếp thì thì hình chóp tứ giác mới có tâm mặt cầu ngoại tiếp.
Câu 13: Mặt cầu tâm O bán kính R = 17dm. Mặt phẳng (P) cắt mặt cầu sao cho giao tuyến đi qua ba điểm A, B, C mà AB=18dm,BC=24dm,CA=30dm. Tính khoảng cách từ O đến (P).
A. 7 dm
B. 8 dm
C. 14 dm
D. 16 dm
Đáp án: B
Giải thích:
Ta có giao tuyến của mặt phẳng (P) với mặt cầu là một đường tròn. Khi đó A, B, C nằm trên đường tròn này, nếu để ý kĩ ta thấy CA2=AB2+BC2, do vậy tam giác ABC vuông tại B, tức là AC chính là đường kính của đường tròn này, hay r=15 dm. Ta có hình vẽ minh họa sau:
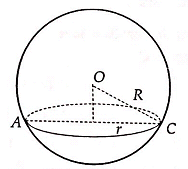
Nhìn vào hình vẽ ta thấy:
d(O;(P))=√R2−r2
=√172−152=8
Câu 14: Thể tích của khối cầu ngoại tiếp hình lập phương ABCD.A'B'C'D' có cạnh bằng 2√3
A. 32π√3
B. 36π
C. 64π√6
D. 4π√3
Đáp án: B
Giải thích:
Thể tích của khối cầu ngoại tiếp hình lập phương ABCD.A'B'C'D' có cạnh bằng 2√3
Mặt cầu ngoại tiếp hình lập phương ABCD.A'B'C'D' có bán kính r=AC'2
mà AC'=2√3.√3
⇒r=2√3.√32=3
Vậy V=43πr3=43π33=36π
Câu 15: Cho tứ diện đều ABCD có cạnh bằng a. Thể tích của khối cầu tiếp xúc với tất cả các cạnh của tứ diện ABCD bằng:
A. √3πa38
B. √2πa324
C. 2√2a39
D. √3a324
Đáp án: B
Giải thích:
Gọi I, J, K, H, M, N lần lượt là trung trung điểm AB, BC, CD, DA, AC, BD. Theo tính chất hình bình hành ta chứng minh được IK, JH, MN cắt nhau tại trung điểm của mỗi đường, gọi giao điểm là O.
Vì ABCD là tứ diện đều
⇒OI=OJ=OK
=OH=OM=ON
và OI⊥AB,OK⊥CD,
OM⊥AC,ON⊥BC
⇒ O là tâm mặt cầu tiếp xúc với các cạnh tứ diện ABCD
Xét hình vuông IJKH cạnh IH=a2
⇒OI=√22IH=a√24=R
⇒V=43πR3=a3π√224 .
Câu 16: Một hình nón có thiết diện qua trục là tam giác đều. Tỉ số thể tích của khối cầu ngoại tiếp và khối cầu nội tiếp khối nón là:
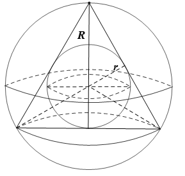
A. 8
B. 6
C. 4
D. 2
Đáp án: A
Giải thích:
Giả sử đường sinh hình nón có độ dài là a. Gọi G là trọng tâm của tam giác thiết diện, do đó G cách đều 3 đỉnh và 3 cạnh của tam giác thiết diện, nên G là tâm của khối cầu ngoại tiếp và khối cầu nội tiếp khối nón, suy ra bán kính R, r của khối cầu ngoại tiếp và khối cầu nội tiếp khối nón, suy ra bán kính R, r của khối cầu ngoại tiếp và khối cầu nội tiếp khối nón lần lượt là a√33,a√36. Gọi V1, V2 lần lượt là thể tích của khối cầu ngoại tiếp và khối cầu nội tiếp khối nón. Vậy V1V2=R3r3=8.
Câu 17: Có một hộp nhựa hình lập phương người ta bỏ vào hộp đó 1 quả bóng đá. Tính tỉ số V1V2, trong đó V1 là tổng thế tích của quả bóng đá, V2 là thể tích của chiếc hộp đựng bóng. Biết rằng đường tròn lớn trên quả bóng có thể nội tiếp 1 mặt hình vuông của chiếc hộp.

A. V1V2=π2
B. V1V2=π4
C. V1V2=π6
D. V1V2=π8
Đáp án: B
Giải thích:
Gọi R là bán kính của mặt cầu, khi đó cạnh của hình lập phương là 2R
Ta được: Thể tích hình lập phương là V2=8R3, thể tích quả bóng là:
V1=4πR33⇒V1V2=π6
Câu 18: Một khối cầu nội tiếp trong hình lập phương có đường chéo bằng 4√3cm. Thể tích của khối cầu là:
A. V=256π3
B. V=64√3π
C. V=32π3
D. V=16√3π
Đáp án: C
Giải thích:
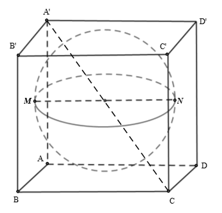
Cho các đỉnh A, B, C, D, A’, B’, C’, D’ như hình vẽ và gọi M, N là tâm các hình vuông ABB’A’ và ADD’C’
Gọi a là độ dài cạnh của hình lập phương.
Ta có:
A'C2=AA'2+AC2
=AA'2+AB2+AD2
=3a2=3.42
⇒a2=16⇒a=4
MN=BC=a=4
⇒ bán kính khối cầu R=2
Thể tích khối cầu là:
V=43π.23=32π3
Câu 19. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AB=2a,AC=a. Mặt bên (SAB), (SCA) lần lượt là các tam giác vuông tại B và C. Biết rằng thể tích khối chóp S.ABC bằng 23a3. Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là:
A. R=√3a2
B. R=a√2
C. R=a
D. R=3a2
Đáp án: D
Giải thích:
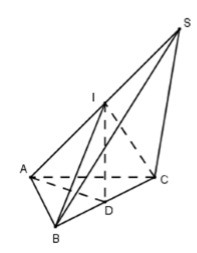
Gọi I là trung điểm của SA
Vì tam giác SAB vuông tại B nên IA=IB=IS
Vì tam giác SAC vuông tại C nên IA=IS=IC
Do đó IA=IB=IC=IS nên I là tâm mặt cầu ngoại tiếp khối chóp S.ABC.
Gọi D là trung điểm của BC ta có D là tâm đường tròn ngoại tiếp tam giác ABC
⇒ID⊥(ABC)
⇒VS.ABC=2VI.ABC=23ID.SABC
⇒ID=3VS.ABC2SABC=2a32a2=a
AD=12BC=a√52
⇒AI=√AD2+ID2
=3a2=R
Câu 20. Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông cân đỉnh A, AB=AC=a,AA'=a√2. Diện tích mặt cầu ngoại tiếp tứ diện CA’B’C’ là:
A. 4πa23
B. 4πa2
C. 12πa2
D. 4√3πa2
Đáp án: B
Giải thích:
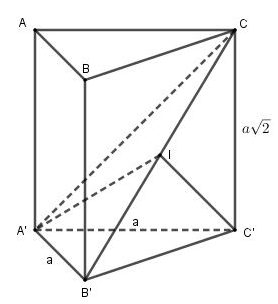
Ta có:
A'B'=AB=a
B'C'=√A'B'2+A'C'2
=√a2+a2=a√2
B'C=√B'C'2+C'C2
=√2a2+2a2=2a
A'C=√A'C'2+C'C2
=√a2+2a2=a√3
⇒A'B'2+A'C2=a2+3a2
=4a2=B'C2
⇒ΔA'B'C vuông tại A’.
Gọi I là trung điểm của B’C thì IB'=IC=IA'
Mà ΔCC'B' vuông tại C’ nên IB'=IC=IC'
Vậy I là tâm mặt cầu ngoại tiếp tứ diện CA’B’C’ và bán kính R=12B'C=a
⇒S=4πR2=4πa2
Câu 21. Cho mặt cầu S(I;R) và mặt phẳng (P) cách l một khoảng bằng R2. Khi đó giao của (P) và (S) là đường tròn có chu vi bằng:
A. 2πR
B. 2πR√3
C. πR√3
D. πR
Đáp án: C
Giải thích:
Ta thấy: d(I;(P))=R2
⇒r=√R2−d2(I;(P))=R√32
Khi đó chu vi đường tròn bằng S=2πr=R√3π
Câu 22. Một hình hộp chữ nhật có độ dài ba cạnh lần lượt là 2; 2; 1. Tính bán kính R của mặt cầu ngoại tiếp hình hộp chữ nhật trên.
A. R = 3
B. R=32
C. R=92
D. R=9
Đáp án: B
Giải thích:
Áp dụng công thức ta có:
R=√a2+b2+c22
=√22+22+122=32
Câu 23. Cho hai khối cầu có bán kính lần lượt bằng a và 2a. Tỉ số thể tích của khối cầu nhỏ với thể tích của khối cầu lớn bằng:
A. 14
B. 4
C. 18
D. 8
Đáp án: C
Giải thích:
Thể tích khối cầu có bán kính r=a là:
V1=43πr3=43πa3
Thể tích khối cầu có bán kính R = 2a là:
V2=43πR3
=43π(2a)3=323πa3
⇒V1V2=43πa3323πa3
=432=18
Câu 24. Cho mặt cầu (S). Biết rằng khi cắt mặt cầu (S) bởi một mặt phẳng cách tâm một khoảng có độ dài là 3 thì được giao tuyến là đường tròn (T) có chu vi là 12π. Diện tích của mặt cầu (S) bằng:
A. 180π
B. 180√3π
C. 90π
D. 45π
Đáp án: A
Giải thích:
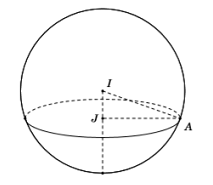
Gọi I, J theo thứ tự là tâm mặt cầu (S) và đường tròn (T), A là điểm bất kì thuộc đường tròn (T). Khi đó ta có:
IJ=3,2π.AJ=12π
⇔AJ=6
Áp dụng định lí Pitago trong tam giác vuông AIJ ta có:
AI=√AJ2+IJ2
=√62+32=3√5
⇒ Bán kính của mặt cầu là R=3√5
Vậy diện tích mặt cầu (S) là:
S=4πR2
=4π.(3√5)2=180π
Câu 25. Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại A, AB=a√3,BC=2a, đường thẳng AC’ tạo với mặt phẳng (BCC’B’) một góc 30°. Diện tích của mặt cầu ngoại tiếp hình lăng trụ đã cho bằng:
A.
B.
C.
D.
Đáp án: A
Giải thích:
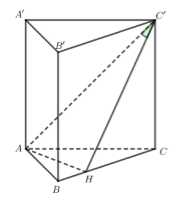
Trong mặt phẳng (ABC) kẻ
Lại có
(do
Ta có:
Gọi R là bán kính mặt cầu ngoại tiếp lăng trụ, khi đó với là bán kính đường tròn ngoại tiếp tam giác vuông ABC và
Do đó
Câu 26. Cho hình hộp chữ nhật ABCD.A’B’C’D’ có . Thể tích khối cầu ngoại tiếp hình hộp chữ nhật ABCD.A’B’C’D’ là:
A.
B.
C.
D.
Đáp án: C
Giải thích:
Bán kính khối cầu ngoại tiếp hình hộp:
Thể tích khối cầu:
Câu 27. Cho một mặt cầu bán kính bằng 2. Xét các hình chóp tam giác đều ngoại tiếp mặt cầu trên. Hỏi thể tích nhỏ nhất của chúng bằng bao nhiêu?
A.
B.
C.
D.
Đáp án: B
Giải thích:
Áp dụng các công thức trong tứ diện đều cạnh a
Bán kính mặt cầu nội tiếp
Thể tích tứ diện đều đó là:
Câu 28. Cho ba hình cầu có bán kính lần lượt là đôi một tiếp xúc nhau và cùng tiếp xúc với mặt phẳng (P). Các tiếp điểm của ba hình cầu với mặt phẳng (P) lập thành một tam giác có độ dài cạnh lần lượt là 2, 3, 4. Tính tổng
A.
B.
C.
D.
Đáp án: D
Giải thích:
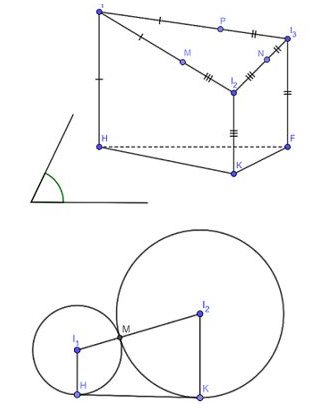
Gọi là tâm của các hình cầu M, N, P là các tiếp điểm của các hình cầu (như hình vẽ), H, K, F là tiếp ba hình cầu với mặt phẳng (P)
Xét mặt phẳng có:
Tương tự:
Vậy
Câu 29. Cho hình chóp tứ giác đều S.ABCD có góc giữa SA và đáy là 60o , SA = 2a. Bán kính mặt cầu ngoại tiếp hình chóp là :
A.
B.
C. 2a
D.
Đáp án: A
Giải thích:
Gọi O là tâm của hình vuông ABCD. Khi đó SO ⊥ (ABCD) và SO là trục của đường tròn ngoại tiếp hình vuông ABCD. Từ giả thiết ta có :
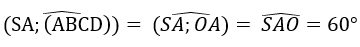
=> SO = SA.sin60o = a√3
Trong mặt phẳng (SAO), đường trung trực của SA cắt SO tại I. Khi đó I cách đều các đỉnh của hình chóp nên I là tâm mặt cầu ngoại tiếp hình chóp. Gọi M là trung điểm của SA, khi đó ta có :
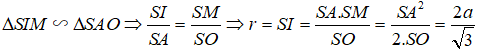
Câu 30. Cho hình chóp S.ABC có đáy là tam giác vuôg cân đỉnh B và BC = a, SA ⊥ (ABC), SA = 2a. Khẳng định nào sau đây là đúng?
A. Điểm S nằm trong mặt cầu tâm A bán kính a
B. Điểm S nằm ngoài mặt cầu tâm A bán kính 2a
C. Điểm C nằm trong mặt cầu tâm A bán kính 2a
D. Cả ba điểm S, B, C cùng nằm trong mặt cầu tâm A bán kính 2a.
Đáp án: C
Giải thích:
Từ giả thiết ta có: SA = 2a; AB = a và AC = a√2 .
Câu 31. Cho mặt cầu (S) tâm O bán kính R và một mặt phẳng (P). Kí hiệu h là khoảng cách từ O đến mặt phẳng (P). Mặt phẳng (P) có nhiều hơn một điểm chung với mặt cầu (S) nếu :
A. h ≤ R
B. h ≥ R
C. h > R
D. h < R
Đáp án: D
Giải thích:
Từ vị trí tương đối của một mặt phẳng với mặt cầu
Chọn đáp án D
Câu 32. Cho mặt cầu (S) tâm O bán kính R và một đường thẳng d. Kí hiệu h là khoảng cách từ O đến đường thẳng d. Đường thẳng d có điểm chung với mặt cầu (S) nếu và chỉ nếu:
A. h ≤ R
B. h = R
C. h > R
D. h < R
Đáp án: A
Giải thích:
Từ vị trí tương đối của một đường thẳng và mặt cầu ta có đường thẳng d có điểm chung với mặt cầu (S) khi và chỉ khi đường thẳng d tiếp xúc hoặc cắt mặt cầu (S).
Câu 33. Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh bằng 2a, SA vuông góc với đáy và SA = a. Bán kính mặt cầu tâm A tiếp xúc với mặt phẳng (SBC) theo a là:
A. 2a
B. a
C. a√2/2
D. 2a√5/5
Đáp án: D
Giải thích:
Ta có mặt cầu S(A;r) tiếp xúc với mặt phẳng (SBC) khi và chỉ khi r = d(A; (SBC)) .
Hạ AH ⊥ SB tại H. Do BC ⊥ AB và BC ⊥ SA nên BC ⊥ (SAB) , suy ra BC ⊥ AH .
Mặt khác AH ⊥ SB nên AH ⊥ (SBC) hay d(A; (SBC)) = AH Xét tam giác vuông SAB ta có:
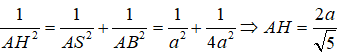
Câu 33. Cho hai quả cầu cùng bán kính là 5cm. Để đựng hai quả cầu Nam phải làm một hình hộp chữ nhật từ bìa carton. Hỏi trong các đáp án dưới đây, Nam cần ít nhất bao nhiêu xen-ti-mét vuông bìa carton để làm được chiếc hộp đó?
A. 300(cm2)
B. 1000(cm2)
C. 250(cm2)
D. 1250(cm2)
Đáp án: B
Giải thích:
Hình hộp chữ nhật đựng được hai quả cầu bán kính 5cm thì độ dài các cạnh ít nhất là 10cm, 10cm, 20cm. Khi đó ta có: Stp = 2 x 102 + 4 x 10 x 20 = 1000(cm2) .
Câu 34. Trong các mệnh đề sau, mệnh đề nào sai?
A. Hình chóp có mặt cầu ngoại tiếp khi và chỉ khi hình chóp có đáy là một tứ giác nội tiếp được đường tròn.
B. Hình chóp có mặt cầu ngoại tiếp nếu nó là hình chóp tam giác
C. Hình chóp có mặt cầu ngoại tiếp nếu nó có các cạnh bên bằng nhau.
D. Hình chóp có mặt cầu ngoại tiếp nếu có cạnh bên vuông góc với đáy.
Đáp án: C
Giải thích:
Hình chóp có mặt cầu ngoại tiếp khi và chỉ khi hình chóp đó có đáy là một đa giác nội tiếp được đường tròn nên mệnh đề A và B đúng. Hình chps có các cạnh bên bằng nhau có hình chiếu vuông góc của đỉnh lên mặt đáy là tâm đường tròn ngoại tiếp đáy nên hình chóp đó có đáy nội tiếp được đường tròn và do đó đáp án C đúng.
Câu 35. Cho khối chóp tam giác S.ABC có SA = 3, SB = 4, SC = 5 và SA, SB, SC đôi một vuông góc. Khối cầu ngoại tiếp tứ diện S.ABC có thể tích là:
A.
B.
C.
D.
Đáp án: B
Giải thích:
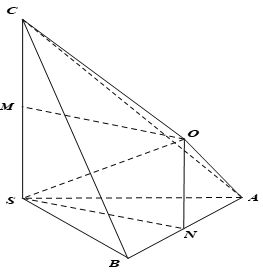
Gọi M,N lần lượt là trung điểm SC, AB
Vì ΔSAB vuông góc tại S nên N là tâm đường tròn ngoại tiếp ΔSAB .
Trong mặt phẳng (MSN) dựng hình chữ nhật MSNO thì ON là trục đường tròn ngoại tiếp ΔSAB và OM là đường trung trực của đoạn SC trong mặt phẳng (OSC)
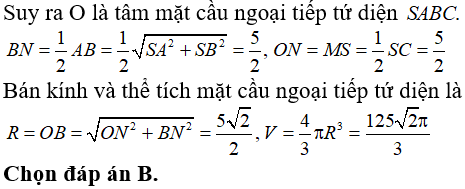
Câu 36. Cho đường thẳng a và điểm A cách đường thẳng a một khoảng bằng 4cm. Trong các mặt cầu đi qua A và tiếp xúc với đường thẳng a, mặt cầu (S) có diện tích nhỏ nhất thì diện tích đó bằng :
A. 4π(cm2)
B. 16π/3(cm2)
C. 16π(cm2)
D. 64π(cm2)
Đáp án: C
Giải thích:
Gọi S(I ;r) là mặt cầu đi qua A và tiếp xúc với a.
Ta có diện tích của mặt cầu là : S = 4πr3 nên S đạt giá trị nhỏ nhất khi và chỉ khi r đạt giá trị nhỏ nhất.
Gọi tiếp điểm của đường thẳng a và mặt cầu là H và hình chiếu vuông góc hạ từ A lên đường thẳng A là A’. Khi đó ta có :
2r = IA + IH ≥ AH ≥ AA' => r ≥ AA'/2 = 2(cm)
Vậy r đạt giá trị nhỏ nhất bằng 2cm khi I là trung điểm của AA’.
Khi đó mặt cầu (S) có diện tích nhỏ nhất là S = 4π22 = 16π(cm2).
Câu 37. Cho mặt cầu (S) tâm O bán kính R và một mặt phẳng (P). Kí hiệu h là khoảng cách từ O đến mặt phẳng (P). Mặt phẳng (P) và mặt cầu (S) có điểm chung nếu và chỉ nếu :
A. h < R
B. h = R
C. h ≤ R
D. h ≥ R
Đáp án: D
Giải thích:
Từ vị trí tương đối của một mặt phẳng và mặt cầu ta có mặt phẳng (P) có điểm chung với mặt cầu (S) khi và chỉ khi mặt phẳng (P) tiếp xúc hoặc cắt mặt cầu (S)
Câu 38. Trong không gian cho đường thẳng Δ và điểm O cách Δ một khoảng bằng 20cm. Mặt cầu (S) tâm O cắt đường thẳng Δ theo một dây có độ dài 30cm có bán kính r bằng :
A. r = 45cm
B. r = 30cm
C. r = 25cm
D. r = 20cm
Đáp án: C
Giải thích:
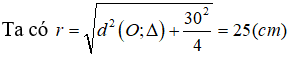
Câu 39. Cho hình chóp tam giác đều S.ABC có SA tạo với đáy một góc bằng 30o và SA=2a. Trong các điểm S, B, C điểm nào nằm trong mặt cầu tâm A bán kính 3a.
A. Không điểm nào
B. Chỉ điểm S
C. Chỉ hai điểm B và C
D. Cả ba điểm
Đáp án: C
Giải thích:
Gọi O là tâm của tam giác đều ABC. Ta có:
góc SAO = 30o => AO = a√3 => AB = AC = 3a
Câu 40. Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh bằng 2a, SAB là tam giác đều. Bán kính mặt cầu tâm A cắt SB theo một dây có độ dài a là:
A. a√13/2
B. 2a
C. 2a√2
D. a√3
Đáp án: C
Giải thích:
Gọi S(A;r) là mặt cầu tâm A cắt đường thẳng SB theo một dây có độ dài a, khi đó ta có:
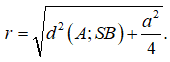
Gọi H là trung điểm của SB. Do tam giác SAB đều nên AH ⊥ SB hay AH là khoảng cách từ A đến SB. Xét tam giác đều SAB ta có :
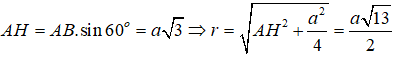
Các câu hỏi trắc nghiệm Toán lớp 12 có đáp án, chọn lọc khác:
Trắc nghiệm Ôn tập Chương 2 - Mặt nón. Mặt trụ. Mặt cầu có đáp án
Trắc nghiệm Hệ tọa độ trong không gian có đáp án
Trắc nghiệm Phương trình mặt phẳng có đáp án
Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án
Trắc nghiệm Ôn tập Chương 3 - Phương pháp tọa độ trong không gian có đáp án
Xem thêm các chương trình khác:
- Trắc nghiệm Sinh học lớp 7 có đáp án
- Trắc nghiệm Toán lớp 7 có đáp án
- Trắc nghiệm Ngữ văn lớp 7 có đáp án
- Trắc nghiệm Sinh học 8 có đáp án
- Trắc nghiệm Toán lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn 8 có đáp án
- Trắc nghiệm Hóa học lớp 8 có đáp án
- Trắc nghiệm Địa Lí lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Tiếng Anh lớp 8 có đáp án
- Trắc nghiệm GDCD lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Lịch sử lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Vật Lí lớp 8 có đáp án
- Trắc nghiệm Công nghệ lớp 8 có đáp án
- Trắc nghiệm Tin học lớp 8 có đáp án
- Trắc nghiệm Sinh học lớp 9 có đáp án
- Trắc nghiệm Toán lớp 9 có đáp án
- Trắc nghiệm Ngữ văn 9 có đáp án
- Trắc nghiệm Hóa học lớp 9 có đáp án
- Trắc nghiệm Địa lí lớp 9 có đáp án
- Trắc nghiệm Tiếng Anh lớp 9 có đáp án
- Trắc nghiệm GDCD lớp 9 có đáp án
- Trắc nghiệm Lịch sử lớp 9 có đáp án
- Trắc nghiệm Vật lí lớp 9 có đáp án
- Trắc nghiệm Công nghệ lớp 9 có đáp án
- Trắc nghiệm Sinh học lớp 10 có đáp án
- Trắc nghiệm Toán lớp 10 có đáp án
- Trắc nghiệm Hóa học lớp 10 có đáp án
- Trắc nghiệm Ngữ văn lớp 10 có đáp án
- Trắc nghiệm Vật Lí lớp 10 có đáp án
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án
- Trắc nghiệm Sinh học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Toán lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Hóa học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn lớp 11 có đáp án
- Trắc nghiệm Tiếng Anh lớp 11 có đáp án
- Trắc nghiệm Vật Lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Địa lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm GDCD lớp 11 có đáp án
- Trắc nghiệm Lịch sử lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Công nghệ lớp 11 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 11 có đáp án
- Trắc nghiệm Tin học lớp 11 có đáp án
