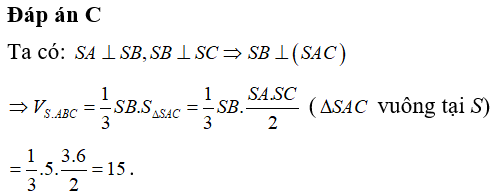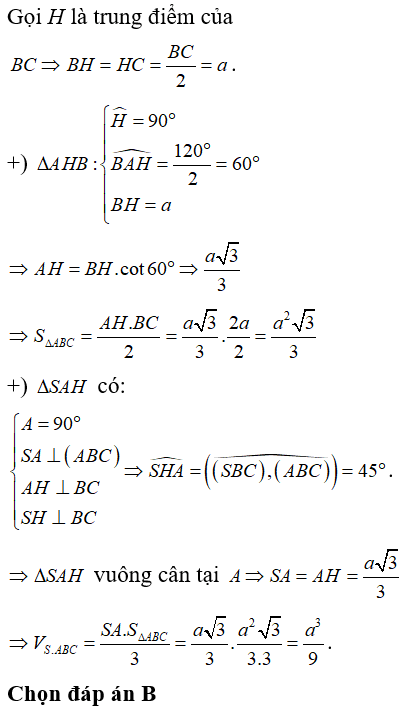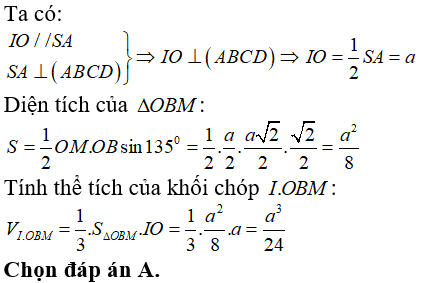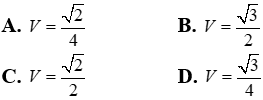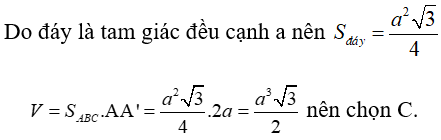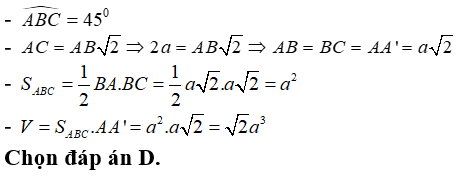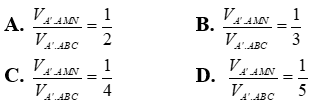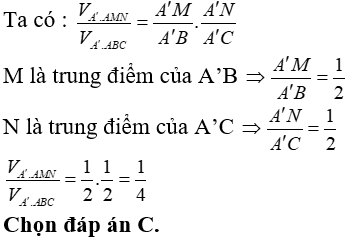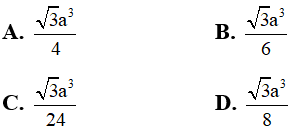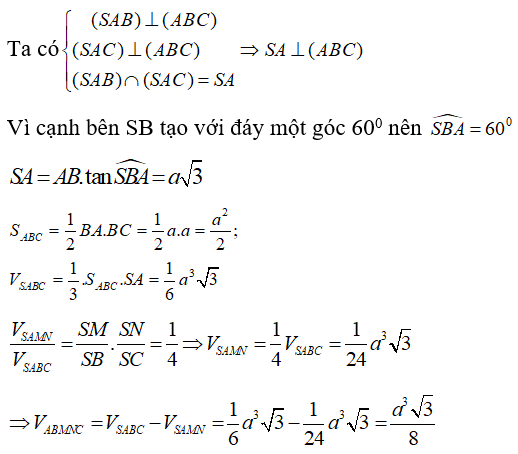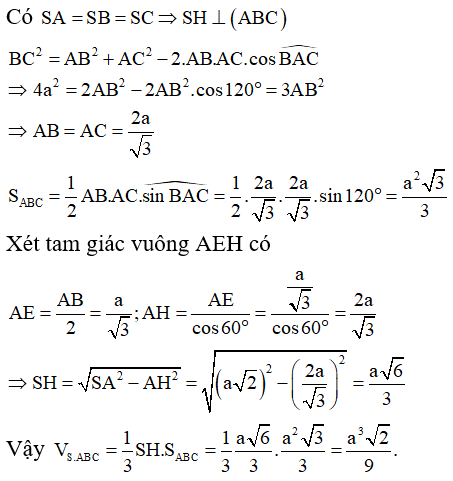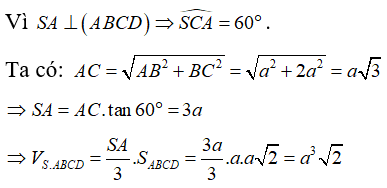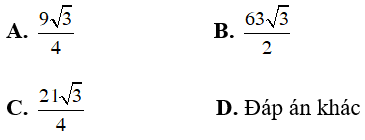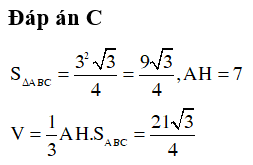TOP 40 câu Trắc nghiệm Khái niệm về thể tích của khối đa diện (có đáp án 2024) - Toán 12

Bộ 40 câu hỏi trắc nghiệm Toán lớp 12 Bài 3: Khái niệm về thể tích của khối đa diện có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 12 Bài 3.

1 1,172 22/12/2023

Tải về

Trang trước

Trang sau

Trắc nghiệm Toán 12 Bài 3: Khái niệm về thể tích của khối đa diện

Bài giảng Trắc nghiệm Toán 12 Bài 3: Khái niệm về thể tích của khối đa diện

Câu 1. Đáy của hình chóp S.ABCD là một hình vuông cạnh a. Cạnh bên SA vuông góc với mặt đáy và có dộ dài là a. Thể tích khối tứ diện S.BCD bằng:

A. $\frac{a^{3}}{6}$

B. $\frac{a^{3}}{3}$

C. $\frac{a^{3}}{4}$

D. $\frac{a^{3}}{8}$

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có:

$S_{Δ B C D} = \frac{1}{2} S_{A B C D} = \frac{1}{2} a^{2}$

$V_{S . B C D} = \frac{1}{3} S A . S_{B C D}$

$= \frac{1}{3} a . \frac{1}{2} a^{2} = \frac{a^{3}}{6}$

Câu 2. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB = a, cạnh bên SC = 3a và SC vuông góc với mặt phẳng đáy. Thể tích khối chóp S.ABC bằng:

A. $\frac{3 a^{3}}{2}$

B. $a^{3}$

C. $\frac{a^{3}}{2}$

D. $3 a^{3}$

Hiển thị đáp án

Đáp án: C

Giải thích:

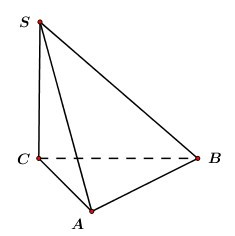
Ta có:

$S_{A B C} = \frac{1}{2} A B^{2} = \frac{1}{2} a^{2}$

$\Rightarrow V_{S . A B C} = \frac{1}{3} S C . S_{A B C}$

$= \frac{1}{3} .3 a . \frac{1}{2} a^{2} = \frac{1}{2} a^{3}$

Câu 3. Cho khối chóp có thể tích V, diện tích đáy là S và chiều cao h. Chọn công thức đúng:

A. $V = S h$

B. $V = \frac{1}{2} S h$

C. $V = \frac{1}{3} S h$

D. $V = \frac{1}{6} S h$

Hiển thị đáp án

Đáp án: C

Giải thích:

Công thức tính thể tích khối chóp $V = \frac{1}{3} S h$

Câu 4. Cho hình hộp ABCD.A’B’C’D’ có thể tích bằng V. Gọi M, N, P, Q, E, F lần lượt là tâm các hình bình hành ABCD, A’B’C’D’, ABB’A’, BCC’B’, CDD’C’, DAA’D’. Thể tích khối đa diện có các đỉnh M, P, Q, E, F, N bằng:

A. $\frac{V}{4}$

B. $\frac{V}{2}$

C. $\frac{V}{6}$

D. $\frac{V}{3}$

Hiển thị đáp án

Đáp án: C

Giải thích:

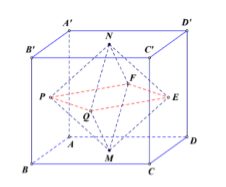
Đặc biệt hóa, coi ABCD.A’B’C’D’ là khối lập phương cạnh bằng 1

$\Rightarrow V_{A B C D . A' B' C' D'} = 1 = V$

Dễ thấy PQEFNM là khối bát diện đều cạnh

$Q E = \frac{1}{2} B D = \frac{\sqrt{2}}{2}$

Vậy

$V_{P Q E F N M} = \frac{{(\frac{\sqrt{2}}{2})}^{3} \sqrt{2}}{3} = \frac{1}{6} = \frac{V}{6}$

Câu 5. Cho khối chóp tam giác S.ABC, trên các cạnh SA, SB, SC lần lượt lấy các điểm A’, B’, C’. Khi đó:

A. $\frac{V_{S . A' B' C'}}{V_{S . A B C}} = \frac{S A'}{S A} + \frac{S B'}{S B} + \frac{S C'}{S C}$

B. $\frac{V_{S . A B C}}{V_{S . A' B' C'}} = \frac{S A'}{S A} . \frac{S B'}{S B} . \frac{S C'}{S C}$

C. $\frac{V_{S . A' B' C'}}{V_{S . A B C}} = \frac{S A'}{S A} = \frac{S B'}{S B} = \frac{S C'}{S C}$

D. $\frac{V_{S . A' B' C'}}{V_{S . A B C}} = \frac{S A'}{S A} . \frac{S B'}{S B} . \frac{S C'}{S C}$

Hiển thị đáp án

Đáp án: D

Giải thích:

Nếu A’, B’, C’ là ba điểm lần lượt nằm trên các cạnh SA, SB, SC của hình chóp tam giác S.ABC thì:

$\frac{V_{S . A' B' C'}}{V_{S . A B C}} = \frac{S A'}{S A} . \frac{S B'}{S B} . \frac{S C'}{S C}$

Câu 6. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên và SA vuông góc với mặt phẳng đáy. Thể tích khối chóp S.ABCD bằng:

A. $a^{3}$

B. $3 a^{3}$

C. $\frac{a^{3}}{3}$

D. $2 a^{3}$

Hiển thị đáp án

Đáp án: A

Giải thích:

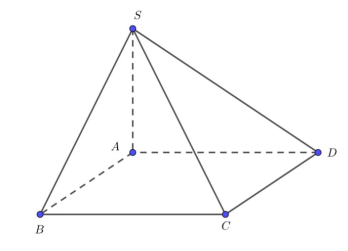
Thể tích khối chóp đã cho là:

$V_{S A B C D} = \frac{1}{3} S A . S_{A B C D}$

$= \frac{1}{3} .3 a . a^{2} = a^{3}$

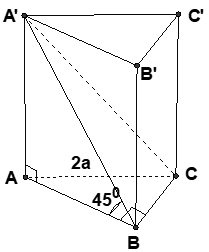
Câu 7. Cho khối lăng trụ đứng ABC.A’B’C’ có đáy là tam giác cân tại C, $A' C = a \sqrt{5}, B C = a, \hat{A C B} = 45 °$ . Thể tích khối lăng trụ ABC.A’B’C’ bằng:

A. $a^{3} \sqrt{3}$

B. $\frac{a^{3} \sqrt{2}}{2}$

C. $\frac{a^{3} \sqrt{2}}{6}$

D. $\frac{a^{3} \sqrt{2}}{12}$

Hiển thị đáp án

Đáp án: B

Giải thích:

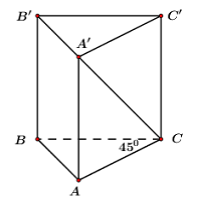
Ta có: $Δ A B C$ cân tại C

$\Rightarrow A C = B C = a$

$\Rightarrow S_{A B C} = \frac{1}{2} A C . B C . \sin C$

$= \frac{1}{2} . a . a . s i n 45 °$

$= \frac{1}{2} a^{2} . \frac{\sqrt{2}}{2} = \frac{a^{2} \sqrt{2}}{4}$

Áp dụng định lí Pitago cho $Δ A A' C$ vuông tại A ta có:

$A A' = \sqrt{A' C^{2} - A C^{2}}$

$= \sqrt{5 a^{2} - a^{2}} = 2 a$

$\Rightarrow V_{A B C . A' B' C'} = A A' . S_{A B C}$

$= 2 a . \frac{a^{2} \sqrt{2}}{4} = \frac{a^{3} \sqrt{2}}{2}$

Câu 8. Nếu khối chóp OABC thỏa mãn $O A = a, O B = b, O C = c$ và $O A ⊥ O B, O B ⊥ O C, O C ⊥ O A$ thì có thể tích là:

A. abc

B. $\frac{a b c}{3}$

C. $\frac{a b c}{2}$

D. $\frac{a b c}{6}$

Hiển thị đáp án

Đáp án: D

Giải thích:

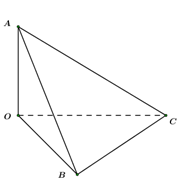
Thể tích khối đa diện OABC là:

$V_{O A B C} = \frac{1}{6} a b c$

Câu 9. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A, SA vuông góc với đáy. Biết $S A = B C = a$ , thể tích khối chóp S.ABC bằng:

A. $\frac{a^{3}}{6}$

B. $\frac{a^{3}}{12}$

C. $\frac{a^{3}}{24}$

D. $\frac{a^{3}}{3}$

Hiển thị đáp án

Đáp án: B

Giải thích:

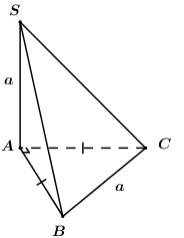
Ta có tam giác ABC vuông cân tại A và

$B C = a \Rightarrow A B = A C = \frac{a}{\sqrt{2}}$

Khi đó:

$S_{A B C} = \frac{1}{2} A B . A C$

$= \frac{1}{2} . \frac{a}{\sqrt{2}} . \frac{a}{\sqrt{2}} = \frac{a^{2}}{4}$

Vậy thể tích khối chóp S.ABC là:

$V_{S . A B C} = \frac{1}{3} S A . S_{Δ A B C}$

$= \frac{1}{3} . a . \frac{a^{2}}{4} = \frac{a^{3}}{12}$

Câu 10. Mệnh đề nào dưới đây sai?

A. Hai khối hộp chữ nhật có diện tích bằng nhau thì có thể tích bằng nhau.

B. Hai khối lăng trụ có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau.

C. Hai khối lập phương có diện tích toàn phần bằng nhau thì có thể tích bằng nhau.

D. Hai khối chóp có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau.

Hiển thị đáp án

Đáp án: A

Giải thích:

Diện tích toàn phần của hình hộp chữ nhật:

$S_{t p} = S_{x q} + 2 a b = 2 h (a + b) + 2 a b$

Thể tích hình hộp chữ nhật:

V = abh

Thể tích của lăng trụ là:

$V = S_{d} . h$

Diện tích toàn phần của khối lập phương:

$S_{t p} = 6 a^{2}$

Thể tích của khối lập phương:

$V = a^{3}$

Thể tích khối chóp là:

$V = \frac{1}{3} S_{d} . h$

Do đó các đáp án B, C, D đúng, chỉ có A sai.

Câu 11. Một khối chóp tam giác có cạnh đáy bằng 6, 8, 10. Một cạnh bên có độ dài bằng 4 và tạo với đáy một góc $60 °$ . Thể tích của khối chóp đó là:

A. 16

B. $8 \sqrt{3}$

C. $48 \sqrt{3}$

D. $16 \sqrt{3}$

Hiển thị đáp án

Đáp án: D

Giải thích:

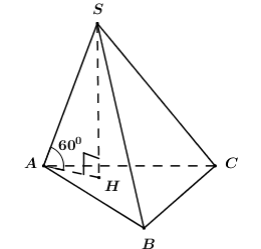
Xét tam giác ABC, giả sử

$A B = 6, B C = 8, A C = 10$

ta có: $A B^{2} + B C^{2} = A C^{2} (= 100)$

nên tam giác ABC vuông tại B (định lí Pitago)

$\Rightarrow S_{Δ A B C} = \frac{1}{2} A B . B C = \frac{1}{2} .6.8 = 24$

Gọi H là hình chiếu vuông góc của S lên (ABC) và giả sử SA hợp với đáy góc $60 °$

HA là hình chiếu của SA lên (ABC)

$\Rightarrow (\hat{S A; (A B C)}) = (\hat{S A; H A})$

$= \hat{S A H} = 60 °$

$\Rightarrow S H = S A . \sin 60 ° = 4. \frac{\sqrt{3}}{2} = 2 \sqrt{3}$

Vậy $V_{S . A B C} = \frac{1}{3} S H . S_{Δ A B C}$

$= \frac{1}{3} .2 \sqrt{3} .24 = 16 \sqrt{3}$

Câu 12. Cho hình chóp S.ABCD đáy là hình chữ nhật, SA vuông góc với đáy, $A B = a, A D = 2 a$ . Góc giữa SB và đáy bằng $45 °$ . Thể tích khối chóp S.ABC bằng:

A. $\frac{a^{3} \sqrt{2}}{3}$

B. $\frac{2 a^{3}}{3}$

C. $\frac{a^{3}}{3}$

D. $\frac{a^{3} \sqrt{2}}{6}$

Hiển thị đáp án

Đáp án: C

Giải thích:

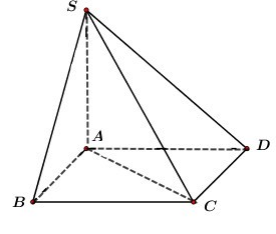
Ta có: $S A ⊥ (A B C D)$

$\Rightarrow A B$ là hình chiếu của SB trên (ABCD)

$\Rightarrow (\hat{S B, (A B C D)}) = (\hat{S B, A B})$

$= \hat{S B A} = 45 °$

$\Rightarrow Δ S A B$ vuông cân tại A

$\Rightarrow S A = A B = a$

$\Rightarrow V_{S . A B C} = \frac{1}{3} S A . S_{A B C}$

$= \frac{1}{3} S A . \frac{1}{2} S_{A B C D}$

$= \frac{1}{3} . a . \frac{1}{2} . a .2 a = \frac{a^{3}}{3}$

Câu 13. Cho khối chóp S.ABCD có thể tích bằng $4 a^{3}$ , đáy ABCD là hình bình hành. Gọi M là trung điểm cạnh SD. Biết diện tích tam giác SAB bằng $a^{2}$ . Tính khoảng cách từ M tới mặt phẳng (SAB)

A. 12a

B. 6a

C. 3a

D. 4a

Hiển thị đáp án

Đáp án: C

Giải thích:

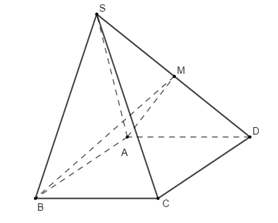
Vì M là trung điểm của SD nên

$\frac{V_{S . A B M}}{V_{S . A B D}} = \frac{S M}{S D} = \frac{1}{2}$

Mà $\frac{V_{S . A B D}}{V_{S . A B C D}} = \frac{1}{2}$

$\Rightarrow V_{S . A B D} = \frac{1}{2} .4 a^{3} = 2 a^{3}$

$\Rightarrow V_{S . A B M} = a^{3} = \frac{1}{3} . d (M; (S A B)) . S_{S A B}$

$\Leftrightarrow d (M; (S A B)) = \frac{3 a^{3}}{a^{2}} = 3 a$

Câu 14. Cho hình chóp S.ABCD có $S A ⊥ (A B C D)$ . Biết $A C = a \sqrt{2}$ , cạnh SC tạo với đáy một góc $60 °$ và diện tích tứ giác ABCD là $\frac{3 a^{2}}{2}$ . Gọi H là hình chiếu của A trên cạnh SC. Tính thể tích khối chóp H.ABCD.

A. $\frac{a^{3} \sqrt{6}}{2}$

B. $\frac{a^{3} \sqrt{6}}{4}$

C. $\frac{a^{3} \sqrt{6}}{8}$

D. $\frac{3 a^{3} \sqrt{6}}{8}$

Hiển thị đáp án

Đáp án: C

Giải thích:

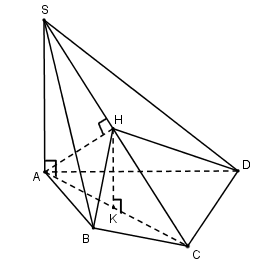
Ta có: $S A ⊥ (A B C D)$

$\Rightarrow$ AC là hình chiếu của SC trên (ABCD)

$\Rightarrow (\hat{S C; (A B C D)}) = (\hat{S C; A C}) = 60 °$

$S A ⊥ (A B C D)$

$\Rightarrow$ $S A ⊥ A C$

$\Rightarrow Δ S A C$ vuông tại A và $\hat{S C A} = 60 °$

Xét tam giác vuông SAC có:

$S A = A C . \tan 60 = a \sqrt{2} . \sqrt{3} = a \sqrt{6}$ ;

$S C = \frac{A C}{\cos 60} = \frac{a \sqrt{2}}{\frac{1}{2}} = 2 a \sqrt{2}$

Áp dụng hệ thức lượng trong tam giác vuông SAC có:

$A C^{2} = H C . S C$

$\Rightarrow \frac{H C}{S C} = \frac{A C^{2}}{S C^{2}} = \frac{2 a^{2}}{8 a^{2}} = \frac{1}{4}$

Trong (SAC) kẻ

$H K / / S A \Rightarrow H K ⊥ (A B C D)$

Ta có:

$\frac{H K}{S A} = \frac{H C}{S C} = \frac{1}{4}$

$\Rightarrow H K = \frac{1}{4} S A = \frac{a \sqrt{6}}{4}$

Vậy $V_{H . A B C D} = \frac{1}{3} H K . S_{A B C D}$

$= \frac{1}{3} . \frac{a \sqrt{6}}{4} . \frac{3 a^{2}}{2} = \frac{a^{3} \sqrt{6}}{8}$

Câu 15. Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc và AB = 2a,

AC = 3a, AD = 4a. Thể tích của khối tứ diện đó là:

A. $12 a^{3}$

B. $6 a^{3}$

C. $8 a^{3}$

D. $4 a^{3}$

Hiển thị đáp án

Đáp án: D

Giải thích:

Thể tích khối tứ diện ABCD đã cho là:

$V = \frac{1}{6} A B . A C . A D = \frac{1}{6} .2 a .3 a .4 a = 4 a^{3}$

Câu 16. Cho khối chóp có chiều cao bằng 6, diện tích đáy bằng 4. Thể tích khối chóp đã cho bằng:

A. 24

B. 10

C. 12

D. 8

Hiển thị đáp án

Đáp án: D

Giải thích:

Thể tích khối chóp đã cho là:

$V = \frac{1}{3} B h = \frac{1}{3} .6.4 = 8$

Câu 17. Công thức tính thể tích lăng trụ có diện tích đáy S và chiều cao h là:

A. $V = \frac{1}{3} S h$

B. $V = \frac{1}{2} S h$

C. $V = \frac{1}{6} S h$

D. V = Sh

Hiển thị đáp án

Đáp án: D

Giải thích:

Công thức tính thể tích lăng trụ có diện tích đáy S và chiều cao h là: V = Sh.

Câu 18. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy (ABCD) và SA = a. Điểm M thuộc cạnh SA sao cho $\frac{S M}{S A} = k$ . Xác định k sao cho mặt phẳng (BMC) chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau.

A. $k = \frac{- 1 + \sqrt{3}}{2}$

B. $k = \frac{- 1 + \sqrt{5}}{2}$

C. $k = \frac{- 1 + \sqrt{2}}{2}$

D. $k = \frac{1 + \sqrt{5}}{4}$

Hiển thị đáp án

Đáp án: B

Giải thích:

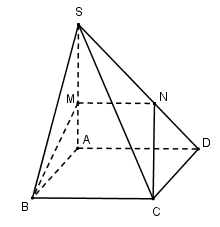
Vì BC // AD nên mặt phẳng (BMC) cắt (SAD) theo đoạn thẳng $M N / / A D (N \in S D)$

Vì $M N / / A D \Rightarrow \frac{S M}{S A} = \frac{S N}{S D} = k$

$\frac{V_{S . M B C}}{V_{S . A B C}} = \frac{S M}{S A} = k$

$\Rightarrow V_{S . M B C} = k . V_{S . A B C} = \frac{k}{2} V_{S . A B C D}$

$\frac{V_{S . M N C}}{V_{S . A D C}} = \frac{S M}{S A} . \frac{S N}{S D} = k^{2}$

$\Rightarrow V_{S . M N C} = k^{2} . V_{S . A D C} = \frac{k^{2}}{2} V_{S . A B C D}$

$\Rightarrow V_{S . M B C N} = V_{S . M B C} + V_{S . M N C}$

$= (\frac{k}{2} + \frac{k^{2}}{2}) V_{S . A B C D}$

Để mặt phẳng (BMNC) chia hình chóp thành 2 phần có thể tích bằng nhau thì:

$\frac{k}{2} + \frac{k^{2}}{2} = \frac{1}{2} \Leftrightarrow k^{2} + k - 1 = 0$

$\Leftrightarrow k = \frac{- 1 + \sqrt{5}}{2}$ do k > 0

Câu 19. Cho hình chóp S.ABC có SA vuông góc với đáy. Tam giác ABC vuông

cân tại B, biết $S A = A C = 2 a$ . Thể tích khối chóp S.ABC là:

A. $V_{S . A B C} = \frac{2}{3} a^{3}$

B. $V_{S . A B C} = \frac{1}{3} a^{3}$

C. $V_{S . A B C} = 2 a^{3}$

D. $V_{S . A B C} = \frac{4}{3} a^{3}$

Hiển thị đáp án

Đáp án: A

Giải thích:

Do $Δ A B C$ vuông cân tại B có

$A C = 2 a \Rightarrow A B = B C = \frac{A C}{\sqrt{2}} = a \sqrt{2}$

$\Rightarrow V_{S . A B C} = \frac{1}{3} S A . \frac{1}{2} B A . B C$

$= \frac{1}{6} .2 a . a \sqrt{2} . a \sqrt{2} = \frac{2 a^{3}}{3}$

Câu 20. Cho hình chóp đều S.ABCD có cạnh AB = a, góc giữa đường thẳng SA và mặt phẳng (ABC) bằng $45 °$ . Thể tích khối chóp S.ABCD là:

A. $\frac{a^{3}}{3}$

B. $\frac{a^{3} \sqrt{2}}{6}$

C. $\frac{a^{3}}{6}$

D. $\frac{a^{3} \sqrt{2}}{3}$

Hiển thị đáp án

Đáp án: B

Giải thích:

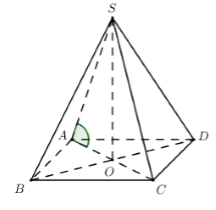
Trắc nghiệm Khái niệm về thể tích của khối đa diện có đáp án - Toán lớp 12 (ảnh 15)

Gọi $O = A C \cap B D$ ta có $S O ⊥ (A B C D)$

$\Rightarrow (\hat{S A; (A B C)}) = (\hat{S A; (A B C D)})$

$= \hat{S A O} = 45 °$

$\Rightarrow S O = O A = \frac{a \sqrt{2}}{2}$

$\Rightarrow V_{S . A B C D} = \frac{1}{3} S O . S_{A B C D}$

$= \frac{1}{3} . \frac{a \sqrt{2}}{2} . a^{2} = \frac{a^{3} \sqrt{2}}{6}$

Câu 21. Cho hình chóp S.ABC đáy ABC là tam giác vuông tại A, AB = 3, AC = $a \sqrt{3}$ . Tam giác SBC đều nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC

A. $V = \frac{a^{3}}{2}$

B. $V = \frac{a^{3}}{6}$

C. $V = \frac{a^{3} \sqrt{3}}{6}$

D. $V = \frac{a^{3} \sqrt{3}}{2}$

Hiển thị đáp án

Đáp án: A

Giải thích:

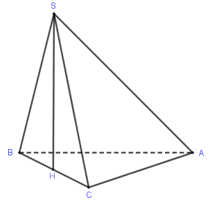
Trong mp (SBC) kẻ

$S H ⊥ B C (H \in B C)$

$\Rightarrow S H ⊥ (A B C)$ , H là trung điểm BC.

Xét tam giác vuông ABC có

$B C = \sqrt{a^{2} + 3 a^{2}} = 2 a$

$\Rightarrow Δ S B C$ đều cạnh 2a

$\Rightarrow S H = \frac{2 a \sqrt{3}}{2} = a {\sqrt{3}}^{3}$

$\Rightarrow V_{S . A B C} = \frac{1}{3} S H . S_{Δ A B C}$

$= \frac{1}{6} S H . A B . A C = \frac{1}{2} a$

Câu 22. Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy là tứ giác đều cạnh a, biết rằng $B D' = a \sqrt{6}$ . Thể tích của khối lăng trụ?

A. $a^{3} \sqrt{2}$

B. $a^{3} \sqrt{3}$

C. $3 a^{3}$

D. $2 a^{3}$

Hiển thị đáp án

Đáp án: D

Giải thích:

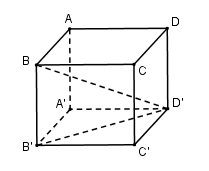
Vì A’B’C’D’ là hình vuông cạnh a nên $B' D' = a \sqrt{2}$

$B B' ⊥ (A' B' C' D')$

$\Rightarrow B B' ⊥ B' D'$

$\Rightarrow Δ B B' D'$ vuông tại B'

$\Rightarrow B B' = \sqrt{B D'^{2} - B' D'^{2}}$

$= \sqrt{6 a^{2} - 2 a^{2}} = 2 a$

Vậy $V_{A B C D . A' B' C' D'} = B B' . S_{A B C D}$

$= 2 a . a^{2} = 2 a^{3}$

Câu 23. Lăng trụ đứng tứ giác có đáy là hình thoi mà các đường chéo là 6cm và 8cm, biết rằng chu vi đáy bằng 2 lần chiều cao lăng trụ. Tính thể tích khối lăng trụ

A. $480 c m^{3}$

B. $360 c m^{3}$

C. $240 c m^{3}$

D. $120 c m^{3}$

Hiển thị đáp án

Đáp án: C

Giải thích:

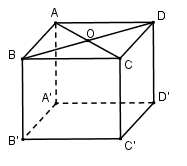
Gọi $O = A C \cap B D$ ta có: OA = 3cm; OB = 4cm.

Xét tam giác vuông OAB có:

$A B = \sqrt{O A^{2} + O B^{2}}$

$= \sqrt{3^{2} + 4^{2}} = 5 c m$

Khi đó chu vi đáy bằng

$P = 4.5 = 20 = 2. A A' \Rightarrow A A' = 10 (c m)$

$S_{A B C D} = \frac{1}{2} A C . B D = \frac{1}{2} .6.8 = 24 (c m^{2})$

Vậy $V_{A B C D . A' B' C' D'} = A A' . S_{A B C D}$

$= 10.24 = 240 (c m^{3})$

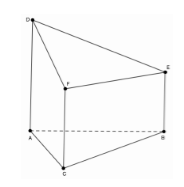
Câu 24. Cho đa diện ABCDEF có AD, BE, CF đôi một song song. $A D ⊥ (A B C), A D + B E + C F = 5$ , diện tích ta giác ABC bằng 10. Thể tích đa diện ABCDEF bằng:

Trắc nghiệm Khái niệm về thể tích của khối đa diện có đáp án - Toán lớp 12 (ảnh 19)

A. 50

B. $\frac{15}{2}$

C. $\frac{50}{3}$

D. $\frac{15}{4}$

Hiển thị đáp án

Đáp án: C

Giải thích:

Chọn $A D = B E = C F = \frac{5}{3}$ thì đa diện hình lăng trụ đứng ABC.DEF có diện tích đáy $S_{A B C} = 10$ , chiều cao $A D = \frac{5}{3}$

Thể tích $V = S_{A B C} . A D = 10. \frac{5}{3} = \frac{50}{3}$

Câu 25. Cho tứ diện ABCD có G là điểm thỏa mãn $\vec{G A} + \vec{G B} + \vec{G C} + \vec{G D} = \vec{0}$ . Mặt phẳng thay đổi chứ BG và cắt AC, AD lần lượt tại M và N. Giá trị nhỏ nhất của tỉ số $\frac{V_{A B M N}}{V_{A B C D}}$ là:

A. $\frac{3}{8}$

B. $\frac{4}{9}$

C. $\frac{1}{2}$

D. $\frac{5}{9}$

Hiển thị đáp án

Đáp án: B

Giải thích:

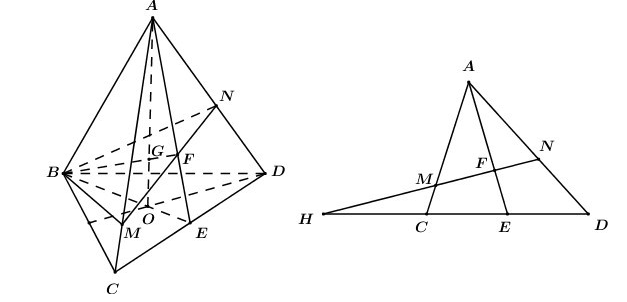
Gọi O là trọng tâm tam giác BCD

$\Rightarrow \vec{G B} + \vec{G C} + \vec{G D} = 3 \vec{G O}$

$\Rightarrow \vec{G A} + 3 \vec{G O} = \vec{0}$

$\Rightarrow \vec{G A} = - 3 \vec{G O}$

$\Rightarrow \frac{A G}{A O} = \frac{3}{4}$

Trong (ABC) gọi $F = B G \cap A E (F \in A E)$

Lấy $M \in A C$ ,

trong (ACD) gọi $N = M F \cap A D (N \in A D)$ ,

khi đó ta có mặt phẳng chứ BG cắt AC, AD lần lượt tại M, N chính là (BMN).

Áp dụng định lí Menelaus trong tam giác AOE, cát tuyến BGF:

$\frac{G A}{G O} . \frac{B O}{B E} . \frac{F E}{F A} = 1$

$\Rightarrow 3. \frac{2}{3} . \frac{F E}{F A} = 1$

$\Rightarrow \frac{F E}{F A} = \frac{1}{2} \Rightarrow \frac{A F}{A E} = \frac{2}{3}$

$\Rightarrow F$ là trọng tâm tam giác ACD

Trong (ACD) kéo dài MN cắt CD tại H.

Đặt $\frac{A M}{A C} = x (0 < x < 1)$

Áp dụng định lí Menelaus trong tam giác ACE, cát tuyến MHF:

$\frac{M A}{M C} . \frac{H C}{H E} . \frac{F E}{F A} = 1$

$\Rightarrow \frac{x}{1 - x} . \frac{H C}{H E} . \frac{1}{2} = 1$

$\Rightarrow \frac{H C}{H E} = \frac{2 (1 - x)}{x}$

$\Rightarrow H E = \frac{x}{2 (1 - x)} H C$

$\Rightarrow H C + C E = \frac{x}{2 (1 - x)} H C$

$\Rightarrow C E = \frac{3 x - 2}{2 (1 - x)} H C$

Ta có:

$H D = H C + 2 C E$

$= H C + \frac{3 x - 2}{1 - x} H C$

$= \frac{2 x - 1}{1 - x} H C$

$\Rightarrow \frac{H E}{H D} = \frac{x}{2 (1 - x)} : \frac{2 x - 1}{1 - x}$

$= \frac{x}{2 (2 x - 1)}$

Áp dụng định lí Menelaus trong tam giác AED, cát tuyến MFN:

$\frac{F A}{F E} . \frac{H E}{H D} . \frac{N D}{N A} = 1$

$\Rightarrow 2. \frac{x}{2 (2 x - 1)} . \frac{N D}{N A} = 1$

$\Rightarrow \frac{N D}{N A} = \frac{2 x - 1}{x} \Rightarrow \frac{N A}{N D} = \frac{x}{2 x - 1}$

$\Rightarrow \frac{N A}{N A + N D} = \frac{x}{x + 2 x - 1} = \frac{x}{3 x - 1}$

$\Rightarrow \frac{A N}{A D} = \frac{x}{3 x - 1}$

Khi đó ta có:

$\frac{V_{A B M N}}{V_{A B C D}} = \frac{A M}{A C} . \frac{A N}{A D}$

$= x . \frac{x}{3 x - 1} = \frac{x^{2}}{3 x - 1} (x > \frac{1}{3})$

Xét hàm số $f (x) = \frac{x^{2}}{3 x - 1} (x > \frac{1}{3})$

ta có:

$f' (x) = \frac{2 x (3 x - 1) - 3 x^{2}}{{(3 x - 1)}^{2}} = \frac{3 x^{2} - 2 x}{{(3 x - 1)}^{2}}$

$f' (x) = 0 \Leftrightarrow [\begin{matrix} x = 0 (k t m) \\ x = \frac{2}{3} \end{matrix}$

BBT:

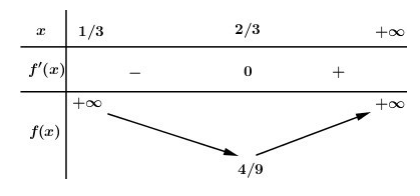
Trắc nghiệm Khái niệm về thể tích của khối đa diện có đáp án - Toán lớp 12 (ảnh 21)

Dựa vào BBT ta thấy

$\min_{(\frac{1}{3}; + \infty)} f (x) = f (\frac{2}{3}) = \frac{4}{9}$

Vậy giá trị nhỏ nhất của tỉ số $\frac{V_{A B M N}}{V_{A B C D}} = \frac{4}{9}$

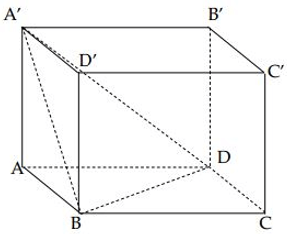
Câu 26. Gọi V là thể tích của hình lập phương ABCD.A'B'C'D' . V₁ là thể tích của tứ diện A'ABD . Hệ thức nào sau đây là đúng ?

A. V = 6V₁

B. V = 4V₁

C. V = 3V₁

D. V = 2V₁

Hiển thị đáp án

Đáp án: A

Giải thích:

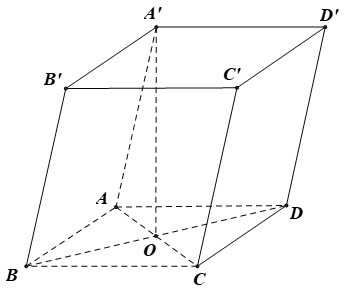
Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Câu 27. Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a, 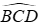Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12 = 120° và AA' = 7a/2 . Hình chiếu vuông góc của A’ lên mặt phẳng (ABCD) trùng với giao điểm của AC và BD. Tính theo a thể tích khối hộp ABCD.A’B’C’D’.

A. V = 12a³

B. V = 3a³

C. V = 9a³

D. V = 6a³

Hiển thị đáp án

Đáp án: B

Giải thích:

Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Câu 28. Cho khối chóp S.ABC với SA ⊥ SB , SB ⊥ SC , SC ⊥SA . Biết độ dài SA, SB, SC lần lượt là 3, 5, 6. Thể tích của khối chóp đó bằng:

A. 20

B. 10

C. 15

D. 30

Hiển thị đáp án

Đáp án: C

Giải thích:

Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Câu 29. Cho hình chóp S.ABC có đáy là tam giác đều. Nếu tăng độ dài cạnh đáy lên 2 lần và độ dài đường cao không đổi thì thể tích S.ABC tăng lên bao nhiêu lần?

A.4 .

B.2 .

C.3 .

D.1/2 .

Hiển thị đáp án

Đáp án: A

Giải thích:

Khi độ dài cạnh đáy tăng lên 2 lần thì diện tích đáy tăng lên 4 lần.

⇒ Thể tích khối chóp tăng lên 4 lần.

Câu 30. Cho khối chóp S.ABC có đáy ABC là tam giác cân tại A với BC = 2a , 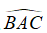Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12 = 120° biết SA ⊥ (ABC) và mặt (SBC) hợp với đáy một góc 45°. Tính thể tích khối chóp S.ABC .

Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Hiển thị đáp án

Đáp án: B

Giải thích:

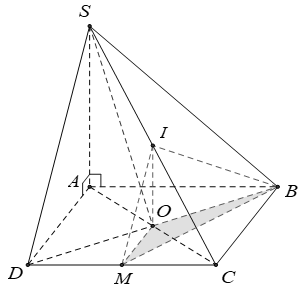
Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Câu 31.Cho hình chóp S.ABCD có cạnh đáy ABCD là hình vuông tâm O cạnh bằng a, SA vuông góc với (ABCD) và SA = 2a . Gọi I là trung điểm của SC và M là trung điểm của DC . Tính thể tích của khối chóp I.OBM .

Hiển thị đáp án

Đáp án: A

Giải thích:

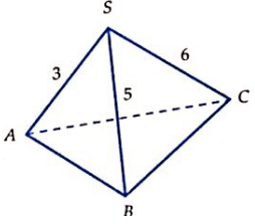
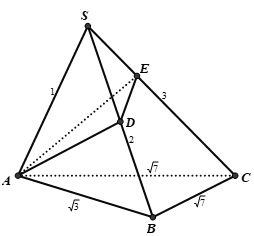
Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Câu 32. Cho hình chóp S.ABC có các cạnh SA = A, SB = 2, SC = 3, AB = √3, BC = CA = √7 . Tính thể tích V khối chóp S.ABC.

Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Hiển thị đáp án

Đáp án: C

Giải thích:

Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Câu 33. Thể tích khối lăng trụ tam giác đều có cạnh đáy bằng a và cạnh bên bằng 2a là:

Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Hiển thị đáp án

Đáp án: C

Giải thích:

Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Câu 34. Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại B và AC = 2a biết rằng (A'BC) hợp với đáy (ABC) một góc 45°. Thể tích lăng trụ là:

Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Hiển thị đáp án

Đáp án: D

Giải thích:

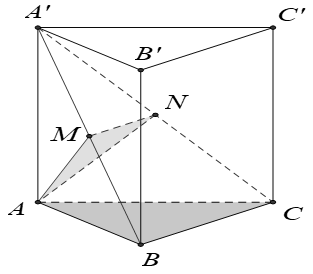
Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Câu 35. Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác đều cạnh bằng a. Mặt bên ABB’A’ có diện tích bằng a²√3 . Gọi M; N lần lượt là trung điểm của A’B; A’C . Tính tỉ số thể tích của hai khối chóp A’. AMN và A’.ABC .

Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Hiển thị đáp án

Đáp án: C

Giải thích:

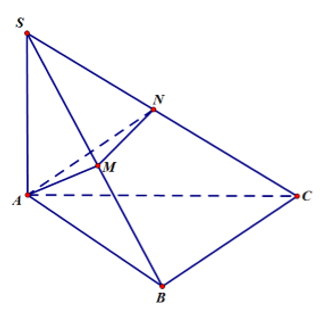
Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Câu 36. Cho hình chóp S.ABC có (SAB),(SAC) cùng vuông góc với mặt phẳng đáy, cạnh bên SB tạo với đáy một góc 60° đáy ABC là tam giác vuông cân tại B với BA = BC = a. Gọi M, N lần lượt là trung điểm của SB, SC. Tính thể tích của khối đa diện A.BMNC

Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Hiển thị đáp án

Đáp án: D

Giải thích:

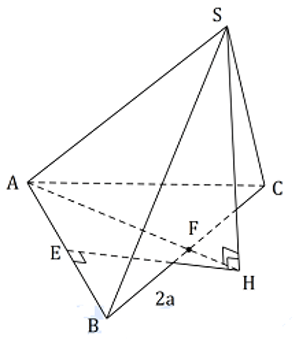
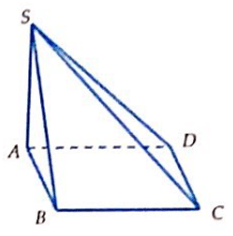
Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Câu 37. Cho hình chóp S.ABC có SA = SB = SC = A√2 và đáy là tam giác ABC cân tại A. Biết 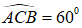Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12 và BC = 2a. Thể tích khối chóp S.ABC là

Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Hiển thị đáp án

Đáp án: C

Giải thích:

Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Đáp án C

Gọi H là tâm đường tròn ngoại tiếp tam giác ABC bằng cách dựng như hình vẽ.

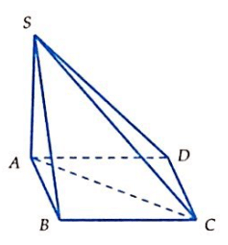
Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Câu 38. Hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB = a, AD = a√2; SA ⊥ (ABCD) , góc giữa SC và đáy bằng 60°. Thể tích hình chóp S.ABCD bằng:

Hiển thị đáp án

Đáp án: A

Giải thích:

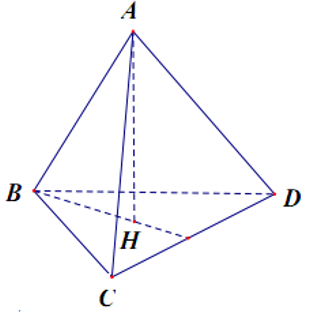
Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Câu 39. Cho hình chóp tam giác đều cạnh bằng 3. Tính thể tích hình chóp đó biết chiều cao h = 7

Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Hiển thị đáp án

Đáp án: C

Giải thích:

Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

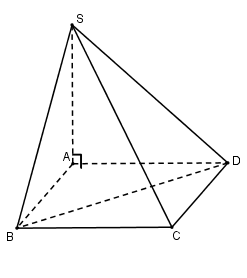
Câu 40. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Cạnh bên SA vuông góc với mặt phẳng đáy, cạnh bên SC tạo với mặt phẳng (SAB) một góc 30°. Thể tích của khối chóp đó bằng:

Hiển thị đáp án

Đáp án: D

Giải thích:

Bài tập trắc nghiệm Hình học 12 | Câu hỏi trắc nghiệm Hình học 12

Các câu hỏi trắc nghiệm Toán lớp 12 có đáp án, chọn lọc khác:

Trắc nghiệm Ôn tập Chương 1 - Khối đa diện có đáp án

Trắc nghiệm Khái niệm về mặt tròn xoay có đáp án

Trắc nghiệm Mặt cầu có đáp án

Trắc nghiệm Ôn tập Chương 2 - Mặt nón. Mặt trụ. Mặt cầu có đáp án

Trắc nghiệm Hệ tọa độ trong không gian có đáp án

1 1,172 22/12/2023

Tải về

Trang trước

Trang sau

Xem thêm các chương trình khác:

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3