Lý thuyết Cực trị của hàm số (mới 2024 + Bài Tập) – Toán 12

Lý thuyết Toán 12 Bài 2: Cực trị của hàm số

Bài giảng Toán 12 Bài 2: Cực trị của hàm số

A. Lý thuyết

I. Khái niệm cực đại, cực tiểu.

- Định nghĩa.

Cho hàm số y = f(x) xác định và liên tục trên khoảng (a; b) (có thể a là $-\infty$; b là $+\infty$) và điểm x₀$\in$(a; b).

a) Nếu tồn tại số h > 0 sao cho f(x) < f(x₀) với mọi x(x₀ – h; x₀ + h) và $x\ne x_0$ thì ta nói hàm số f(x) đạt cực đại tại x₀.

b) Nếu tồn tại số h > 0 sao cho f(x) > f(x₀) với mọi x$\in$(x₀ – h; x₀ + h) và $x\ne x_0$ thì ta nói hàm số f(x) đạt cực tiểu tại x₀.

- Chú ý:

1. Nếu hàm số f(x) đạt cực đại (cực tiểu) tại x₀ thì x₀ được gọi là điểm cực đại (điểm cực tiểu) của hàm số; f(x₀) được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số.

Kí hiệu là f_CĐ (f_CT) còn điểm M(x₀; f(x₀)) được gọi là điểm cực đại (điểm cực tiểu) của đồ thị hàm số.

2. Các điểm cực đại, cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại (giá trị cực tiểu) còn gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số.

3. Dễ dàng chứng minh được rằng, nếu hàm số y = f(x) có đạo hàm trên khoảng (a; b) và đạt cực đại hoặc cực tiểu tại x₀ thì f’(x₀) = 0.

II. Điều kiện đủ để hàm số có cực trị

- Định lí 1

Giả sử hàm số y = f(x) liên tục trên khoảng K = (x₀ – h; x₀ + h) và có đạo hàm trên K hoặc trên K \ {x₀}; với h > 0.

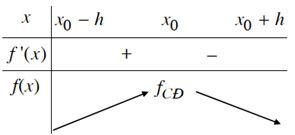
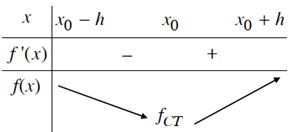
a) Nếu f’(x) > 0 trên khoảng (x₀ – h; x₀) và f’(x) < 0 trên khoảng (x₀; x₀ + h) thì x₀ là một điểm cực đại của hàm số f(x).

b) Nếu f’(x) < 0 trên khoảng (x₀ – h; x₀) và f’(x) > 0 trên khoảng (x₀; x₀ + h) thì x₀ là một điểm cực tiểu của hàm số f(x).

Ví dụ 1. Tìm các điểm cực trị của hàm số y = – 2x³ + 3x².

Lời giải:

Hàm số xác định với mọi x.

Ta có: y’ = – 6x² + 6x

Và y’ = 0$\iff \left[\begin{array}{c}x=0\\ x=1\end{array}\right.$

Bảng biến thiên:

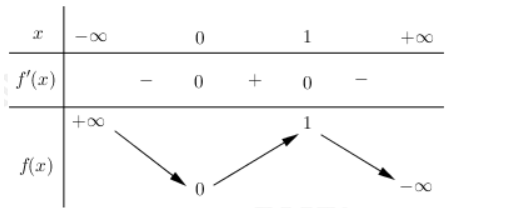
Từ bảng biến thiên, suy ra x = 0 là điểm cực tiểu của hàm số và x = 1 là điểm cực đại của hàm số.

Ví dụ 2. Tìm các điểm cực trị của hàm số $y=\frac{2-x}{2x+\text{\hspace{0.17em}}2}$

Lời giải:

Hàm số đã cho xác định với $\forall x\ne -1$

Ta có: $y\text{'}=\frac{-6}{(2x+\text{}2){}_2}<0$$\forall x\ne -1$

Vậy hàm số đã cho không có cực trị (vì theo khẳng định 3 của chú ý trên, nếu hàm số đạt cực trị tại x₀ thì y’(x₀) = 0).

III. Quy tắc tìm cực trị.

- Quy tắc 1.

1. Tìm tập xác định.

2. Tính f’(x). Tìm các điểm tại đó f’(x) bằng 0 hoặc f’(x) không xác định.

3. Lập bảng biến thiên.

4. Từ bảng biến thiên suy ra các điểm cực trị.

- Định lí 2.

Giả sử hàm số y = f(x) có đạo hàm cấp hai trong khoảng (x₀ – h; x₀ + h) với h > 0. Khi đó:

a) Nếu f’(x₀) = 0; f”(x₀) > 0 thì x₀ là điểm cực tiểu;

b) Nếu f’(x₀) = 0; f”(x₀) < 0 thì x₀ là điểm cực đại.

- Quy tắc II.

1. Tìm tập xác định

2. Tính f’(x). Giải phương trình f’(x) = 0 và kí hiệu x_i ( i = 1; 2; ….; n) là các nghiệm của nó.

3. Tính f”(x) và f”(x_i).

4. Dựa vào dấu của f”(x_i) suy ra tính chất cực trị của điểm x_i.

- Ví dụ 4. Tìm cực trị của hàm số $f\left(x\right)=x^4-2x^2+\text{\hspace{0.17em}\hspace{0.17em}}10$.

Lời giải:

Hàm số đã cho xác định với mọi x

Ta có: f’(x) = 4x³ – 4x

$f\text{'}\left(x\right)=0$$\hspace{0.17em}\iff \left[\begin{array}{c}x=0\\ x=\pm 1\end{array}\right.$

Ta có: f”(x) = 12x² – 4

Suy ra: f”(0) = – 4 < 0 nên x = 0 là điểm cực đại.

f”(1) = f”(– 1) = 8 > 0 nên x = 1 và x = –1 là điểm cực tiểu.

Kết luận:

Hàm số f(x) đạt cực tiểu tại x = 1 và x = – 1; f_CT = f(1) = f(–1) = 9.

Hàm số f(x) đạt cực đại tại x = 0 và f_CD = f(0) = 10.

B. Bài tập tự luyện

Bài 1. Áp dụng quy tắc I, hãy tìm các điểm cực trị của các hàm số sau:

a) y = x⁴ – 2x³ + x² – 8;

b) $y=\frac{x-3}{x+4}$

Lời giải:

a) TXĐ: D = .

Ta có: y’ = 4x³ – 6x² + 2x

$y\text{'}=0$$\iff \left[\begin{array}{c}x=1\\ x=\frac{1}{2}\\ x=0\end{array}\right.$

Bảng biến thiên:

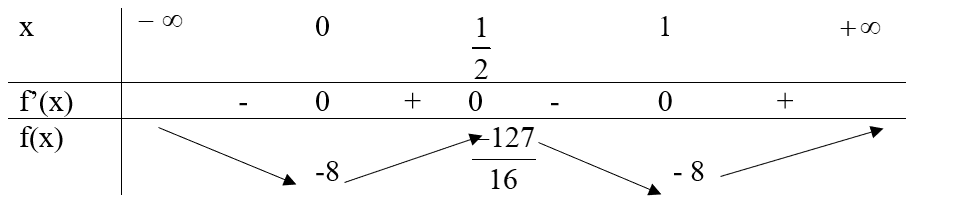
Hàm số đạt cực tiểu tại x = 0 và x = 1; f_CT = f(0) = f(1) = – 8

Hàm số đạt cực đại tại $x=\frac{1}{2};$$\hspace{0.17em}{f}_{CD}=\frac{-127}{16}$

b) $y=\frac{x-3}{x+4}$

TXĐ: D = R\{– 4}.

$y\text{'}=\frac{7}{{(x\text{\hspace{0.17em}}+4)}^2}>0$$\forall x\ne -4$

Phương trình y’ = 0 vô nghiệm nên hàm số không có cực trị.

Bài 2. Áp dụng quy tắc II, hãy tìm các điểm cực trị của các hàm số sau:

a) y = 2x⁴ – 4x² + 2;

b) y = x⁵ – 2x³ + x + 1;

c) $y=x^2+\frac{2}{x}$

Lời giải:

a) y = 2x⁴ – 4x² + 2

TXĐ: D = R.

Ta có: y’ = 8x³ – 8x.

$y\text{'}=0$$\hspace{0.17em}\iff \left[\begin{array}{c}x=0\\ x=\pm 1\end{array}\right.$

Đạo hàm cấp hai: y” (x) = 24x² – 8

Vì y”(– 1) = 16 > 0; y”(1) = 16 > 0 nên hàm số đạt cực tiểu tại x = – 1; x = 1 và y_CT = y(1) = y(– 1) = 0.

và y” (0) = –8 < 0 nên hàm số đạt cực đại tại x = 0 và y_CD = y(0) = 2.

b) y = x⁵ – 2x³ + x + 1

TXĐ: D = R.

Ta có: y’ = 5x⁴ – 6x² + 1

$y\text{'}=0$$\hspace{0.17em}\iff \left[\begin{array}{c}x=\pm 1\\ x=\pm \frac{1}{\sqrt{5}}\end{array}\right.$

Đạo hàm cấp hai: y” = 20x³ – 12x

Và y”(1) = 8 > 0 nên hàm số đạt cực tiểu tại x = 1.

y”(– 1) = – 8 < 0 nên hàm số đạt cực đại tại x = – 1.

$y"\left(\frac{1}{\sqrt{5}}\right)\text{}$$\hspace{0.17em}\hspace{0.17em}=\text{\hspace{0.17em}\hspace{0.17em}}\frac{-8\sqrt{5}}{5}\text{\hspace{0.17em}\hspace{0.17em}}<0$ nên hàm số đạt cực đại tại $x=\frac{1}{\sqrt{5}}$

$y"\left(\frac{-1}{\sqrt{5}}\right)\text{}$$\hspace{0.17em}\hspace{0.17em}=\text{\hspace{0.17em}\hspace{0.17em}}\frac{8\sqrt{5}}{5}\text{\hspace{0.17em}\hspace{0.17em}}>0$ nên hàm số đạt cực tiểu tại $x=-\frac{1}{\sqrt{5}}$

Vậy hàm số đã cho có 2 điểm cực đại, 2 điểm cực tiểu.

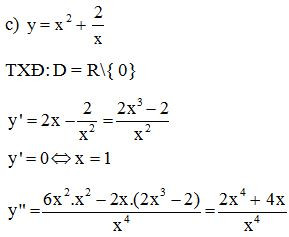
y”(1) = 6 > 0 nên hàm số đạt cực tiểu tại x = 1 và y_CT = y(1) = 3.

Bài 3. Tìm tất cả các giá trị của tham số m để hàm số y = x³ – mx² + (2m – 3).x – 3 đạt cực đại tại x = 1.

Lời giải:

TXĐ: D = R.

Và y’ = 3x² – 2mx + 2m – 3;

y” (x) = 6x – 2m

Để hàm số đã cho đạt cực đại tại x = 1 thì:

$$\begin{gathered} \left\{\begin{array}{c}y\text{'}\left(1\right)=0\\ y"\left(1\right)<0\end{array}\right. \\ \iff \left\{\begin{array}{c}3-2m+2m-3=0\\ 6-2m<0\end{array}\right. \\ \hspace{0.17em}\iff \left\{\begin{array}{c}0=0\left(ld\right)\\ m>3\end{array}\right.\iff m>\text{\hspace{0.17em}}3 \end{gathered}$$

Vậy để hàm số đã cho đạt cực đại tại x = 1 thì m > 3.

Trắc nghiệm Toán 12 Bài 2: Cực trị hàm số

Câu 1. Tìm giá trị cực đại y_CĐ của hàm số y = x³ - 3x +2

A. y_CĐ = 4

B. y_CĐ = 1

C. y_CĐ = 0

D. y_CĐ = -1

Câu 2. Cho hàm số $\frac{x^2+3}{x+1}$ . Mệnh đề nào dưới đây đúng?

A. Cực tiểu của hàm số bằng -3

B. Cực tiểu của hàm số bằng -6

C. Cực tiểu của hàm số bằng 1

D. Cực tiểu của hàm số bằng 2

Câu 3. Đồ thị của hàm số y = x³ - 3x² - 9x +1 có hai điểm cực trị A và B. Điểm nào dưới đây thuộc đường thẳng AB?

A. P(1;0)

B. M(0;1)

C. N (1;-10)

D. Q(-1;10)

Câu 4. Đồ thị của hàm số y = -x³ + 3x +5 có hai điểm cực trị A và B. Tính diện tích S của tam giác OAB với O là gốc tọa độ.

A. S = 9

B. S = $\frac{10}{3}$

C. S = 5

D. S = 10

Câu 5. Cực đại (giá trị cực đại) của hàm số $y=-x^4+2x^2-2$ bằng

A. 1

B. -1

C. -2

D. 0

Câu 6. Cực tiểu (giá trị cực tiểu) của hàm số $y=-\frac{1}{4}{x}^4+8x^2-3$ bằng:

A. -4

B. 4

C. -3

D. 0

Câu 7. Số điểm cực trị của hàm số y = x³+x²+3x-1 là

A. 1

B. 0

C. 2

D. 3

Câu 8. Tìm điểm cực tiểu của đồ thị hàm số y = x³ -3x² -1?

A. (0;-2)

B. (0;1)

C. (5;-2)

D. (2;-5)

Câu 9. Số điểm cực trị của hàm số $y=\frac{x^2-x-2}{x+1}$ là

A. 0

B. 1

C. 2

D. 3

Câu 10. Hàm số nào sau đây không có điểm cực trị

A. y = x²

B. y = x³

C. y = x⁴

D. y = -x²

Xem thêm các bài tổng hợp lý thuyết Toán lớp 12 đầy đủ, chi tiết khác:

Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Lý thuyết Đường tiệm cận

Lý thuyết Khảo sát sự biến thiên và vẽ đồ thị hàm số

Lý thuyết Ôn tập chương 1

Lý thuyết Lũy thừa