Lý thuyết Ứng dụng của tích phân trong hình học (mới 2024 + Bài Tập) – Toán 12

Lý thuyết Toán 12 Bài 3: Ứng dụng của tích phân trong hình học

Bài giảng Toán 12 Bài 3: Ứng dụng của tích phân trong hình học

A. Lý thuyết

I. Tính diện tích hình phẳng

1. Hình phẳng giới hạn bởi một đường cong và trục hoành

Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) liên tục trên đoạn [a; b], trục hoành và hai đường thẳng x = a; x = b được xác định: $S=\underset{a}{\overset{b}{\int }}\left|f\left(x\right)\right|dx$

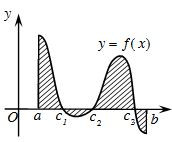
Ví dụ 1. Tính diện tích hình phẳng được giới hạn bởi y = 5x⁴ + 3x², trục hoành và hai đường thẳng x = 0; x = 1.

Lời giải:

Diện tích hình phẳng cần tính là:

$\begin{array}{l}S=\underset{0}{\overset{1}{\int }}\left|5x^4+3x^2\right|dx\\ =\underset{0}{\overset{1}{\int }}\left(5x^4+3x^2\right)dx\\ ={\left.\left(x^5+\text{\hspace{0.17em}}{x}^3\right)\right|}_0^1=2\end{array}$

2. Hình phẳng được giới hạn bởi 2 đường cong

Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x); y = g(x) liên tục trên đoạn [a; b] và hai đường thẳng x = a; x = b được xác định:

$S=\underset{a}{\overset{b}{\int }}\left|f\left(x\right)-g\left(x\right)\right|dx$(*).

- Chú ý.

Khi áp dụng công thức (*), cần khử dấu giá trị tuyệt đối của hàm số dưới dấu tích phân. Muốn vậy ta giải phương trình: f(x) – g(x) = 0 trên đoạn [a; b].

Giả sử phương trình có hai nghiệm c; d (c < d). Khi đó, f(x) – g(x) không đổi dấu trên các đoạn [a; c]; [c; d]; [d; b]. Trên mỗi đoạn đó, chẳng hạn trên [a; c] ta có:

$\underset{a}{\overset{c}{\int }}\left|f\left(x\right)-g\left(x\right)\right|dx$$\hspace{0.17em}=\left|\underset{a}{\overset{c}{\int }}\left[f\left(x\right)-g\left(x\right)\right]dx\right|$

Ví dụ 2. Tính diện tích hình phẳng được giới hạn bởi các đường thẳng x = 0; x = 2 và các đồ thị của hai hàm số y = x – 1 và y = x² – 1.

Lời giải:

Phương trình hoành độ giao điểm của hai đường cong:

II. Tính thể tích

1. Thể tích của vật thể

Cắt một vật thể (H) bởi hai mặt phẳng (P) và (Q) vuông góc với trục Ox lần lượt tại x = a; x = b (a < b). Một mặt phẳng tùy ý vuông góc với Ox tại điểm x $(a\le x\le b)$ cắt (H) theo thiết diện có diện tích là S(x). Giả sử S(x) liên tục trên đoạn [a; b].

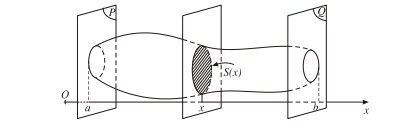
Khi đó, thể tích V của phần vật thể giới hạn bởi hai mặt phẳng (P) và (Q) được xác định bởi công thức: $V=\underset{a}{\overset{b}{\int }}S\left(x\right)dx$

2. Thể tích khối chóp và khối chóp cụt.

a) Cho khối chóp có diện tích đáy là B, chiều cao h.

Khi đó, thể tích của khối chóp là $V=\frac{1}{3}B.h$

b) Cho khối chóp cụt tạo bởi khối chóp đỉnh S có diện tích hai đáy lần lượt là B; B’ và chiều cao là h.

Thể tích của khối chóp cụt là:

$V=\frac{h}{3}$$\left(B+\sqrt{B.B\text{'}}+\text{\hspace{0.17em}}B\text{'}\right)$

III. Thể tích khối tròn xoay

- Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường cong y = f(x), trục hoành và hai đường thẳng x = a; x = b quanh trục Ox:

$V=\pi \underset{a}{\overset{b}{\int }}{f}^2\left(x\right)dx$

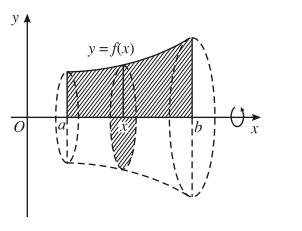
Ví dụ 3. Cho hình phẳng giới hạn bởi đường cong , trục hoành và hai đường thẳng x = 0; x = 2. Tính thể tích khối tròn xoay thu được khi quay hình này quanh trục Ox.

Lời giải:

Thể tích khối tròn xoay cần tính là:

$V=\pi \underset{0}{\overset{2}{\int }}{x}^{4}dx$$=\pi {\left.\frac{x^5}{5}\right|}_0^2=\frac{32\pi }{5}$

B. Bài tập tự luyện

Bài 1. Tính diện tích hình phẳng giới hạn bởi các đường sau:

a) y = x³ ; y = 4x;

b) y = x³, trục hoành và hai đường thẳng x = 1 ; x = 3;

c) y = x³ – 3x² , trục hoành và hai đường thẳng x = 1; x = 4;

d) y = 2 – x²; y = –x.

Lời giải:

a) Phương trình hoành độ giao điểm của hai đồ thị:

b) Ta có trên đoạn [1; 3] nên diện tích hình phẳng cần tính là:

$$\begin{gathered} S=\underset{1}{\overset{3}{\int }}\left|x^3\right|dx \\ =\underset{1}{\overset{3}{\int }}{x}^{3}dx={\left.\frac{{\displaystyle x^4}}{{\displaystyle 4}}\right|}_1^3=20 \end{gathered}$$

d) Phương trình hoành độ giao điểm của hai đồ thị :

Bài 2. Tính diện tích hình phẳng giới hạn bởi parabol (P): y = x² + 3, tiếp tuyến của (P) tại điểm có hoành độ x = 2 và trục tung?

Lời giải:

Ta có: y’ = 2x .

Suy ra: y’(2) = 4 và y(2) = 7.

Phương trình tiếp tuyến của (P) tại điểm có hoành độ x = 2 là

y = 4(x – 2) + 7 = 4x – 1 .

Xét phương trình hoành độ giao điểm của (P) và tiếp tuyến:

x² + 3 = 4x – 1x² – 4x + 4 = 0

$\iff$x = 2

Diện tích hình phẳng cần tính là:

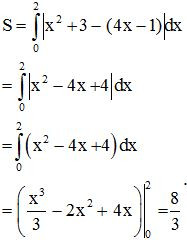
Bài 3. Tính thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường sau quay quanh Ox.

a) y = x³ + 1; y = 0; x = 0; x = 1

b) y = –x² + 2x; y = 0

c) y = $\sqrt{\ln x}$; y = 0; x = 2.

Lời giải:

a) Theo công thức ta có thể tích của khối tròn xoay cần tính là:

$\begin{array}{l}V=\pi \underset{0}{\overset{1}{\int }}{(x^3+1)}^{2}dx\\ \hspace{0.17em}=\pi \underset{0}{\overset{1}{\int }}\left(x^6+2x^3+1\right)dx\\ ={\left.\pi \left(\frac{x^7}{7}+\frac{x^4}{2}+\text{}x\right)\right|}_0^1=\frac{23\pi }{14}.\end{array}$

b) Phương trình hoành độ giao điểm của hai đồ thị là:

– x² + 2x = 0$\iff \left[\begin{array}{c}x=0\\ x=2\end{array}\right.$

Theo công thức ta có thể tích của khối tròn xoay cần tính là:

$\begin{array}{l}V=\pi \underset{0}{\overset{2}{\int }}{(-x^2+2x)}^{2}dx.\\ =\pi \underset{0}{\overset{2}{\int }}(x^4+4x^2-4x^3)dx\\ =\pi {\left.\left(\frac{x^5}{5}\text{\hspace{0.17em}\hspace{0.17em}}+\frac{4x^3}{3}-x^4\right)\right|}_0^2=\frac{16\pi }{15}\end{array}$

c) Phương trình hoành độ giao điểm của hai đồ thị là:

$\sqrt{\ln x}$ = 0$\iff$x = 1

Vậy thể tích của khối tròn xoay cần tính là:

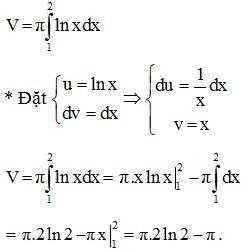
Trắc nghiệm Toán 12 Bài 3: Ứng dụng tích phân

Câu 1. Tính diện tích các hình phẳng giới hạn bởi: Đồ thị các hàm số $y=x^2-4,y=-x^2-2x$ và hai đường thẳng $x=-3,x=-2$;

A. $\frac{11}{6}$

B. $\frac{11}{3}$

C. $\frac{22}{3}$

D. $\frac{19}{3}$

Hiển thị đáp án

Đáp án: B

Giải thích:

Dựa vào hình vẽ ta thấy diện tích hình phẳng cần tìm là:

$S={\int }_{-3}^{-2}\left|\left(x^2-4\right)-\left(-x^2-2x\right)\right|dx$

$={\int }_{-3}^{-2}\left[\left(x^2-4\right)-\left(-x^2-2x\right)\right]dx$

$={\int }_{-3}^{-2}\left(2x^2+2x-4\right)dx$

$=\left(2\frac{x^3}{3}+2\frac{x^2}{2}-4x\right)\left|\begin{array}{c}-2\\ -3\end{array}\right.=\frac{11}{3}$

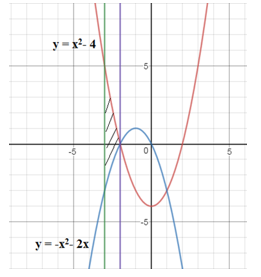
Câu 2: Đồ thị hai hàm số $y=x^2-4$ và $y=-x^2-2x$

A. 8

B. 10

C. 20

D. 9

Hiển thị đáp án

Đáp án: D

Giải thích:

Phương trình hoành độ giao điểm đồ thị hai số đã cho là:

$x^2-4=-x^2-2x$

$\iff x^2+x-2=0$

$\iff \left[\begin{array}{c}x=1\\ x=-2\end{array}\right.$

Dựa vào hình vẽ ở câu A. ta có:

$S={\int }_{-2}^1\left|\left(x^2-4\right)-\left(-x-2x\right)\right|dx$

$={\int }_{-2}^1\left[-\left(2x^2+2x-4\right)\right]dx$

$=\left(-2\frac{x^3}{3}-2\frac{x^2}{2}+4x\right)\left|\begin{array}{c}1\\ -2\end{array}=9\right.$

Câu 3: Đồ thị hàm số $y=x^3-4x$ , trục hoành, đường thẳng $x=-2$ và đưởng thẳng $x=4$.

A. 44

B. 24

C. 48

D. 28

Hiển thị đáp án

Đáp án: A

Giải thích:

Diện tích cần tìm $S={\int }_{-2}^1\left|x^3-4x\right|dx$

Ta có: $x^3-4x=x\left(x^2-4\right)=0$

$\iff \left[\begin{array}{c}x=0\\ x=\pm 2\end{array}\right.$

Ta có bảng xét dấu sau:

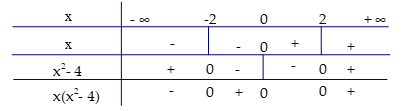
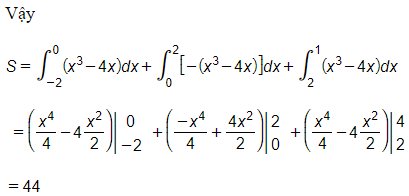
Câu 4: Hàm số $y=x^4-4x^2+4,y=x^2$, trục tung và đường thẳng

A. $\frac{38}{25}$

B. $\frac{38}{35}$

C. $\frac{38}{15}$

D. $\frac{38}{5}$

Hiển thị đáp án

Đáp án: C

Giải thích:

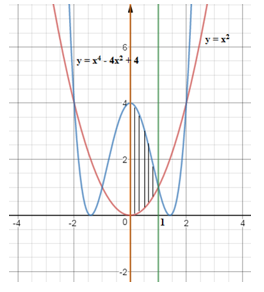
Diện tích hình phẳng cần tìm là:

$S={\int }_0^1\left|x^4-4x^2+4-x^2\right|dx$

$={\int }_0^1\left|x^4-5x^2+4\right|dx$

Vì $x^4-5x^2+4=\left(x^2-1\right)\left(x^2-4\right)\ge 0$

$\forall x\in \left[0;1\right]$

Nên

$S={\int }_0^1\left(x^4-5x^2+4\right)dx$

$=\left(\frac{x^5}{5}-\frac{5x^3}{3}+4x\right)\left|\begin{array}{c}1\\ 0\end{array}\right.$

$=\frac{1}{5}-\frac{5}{3}+4=\frac{38}{15}$

Câu 5: Tính diện tích hình phẳng giới hạn bởi đồ thị hai hàm số $y=x^2+1$ và $y=3-x$

A. $\frac{6}{2}$

B. $\frac{5}{2}$

C. $\frac{11}{2}$

D. $\frac{9}{2}$

Hiển thị đáp án

Đáp án: D

Giải thích:

Hoành độ giao điểm đồ thị hai hàm số $y=x^2+1$ và $y=3-x$ là nghiệm của phương trình $x^2+1=3-x$

$\iff x^2+x-2=0$

$\iff \left[\begin{array}{c}x=1\\ x=-2\end{array}\right.$

Vậy diện tích cần tìm là:

$S={\int }_{-2}^1\left|\left(x^2+1\right)-\left(3-x\right)\right|dx$

$={\int }_{-2}^1\left|x^2+x-2\right|dx$

$=-{\int }_{-2}^1\left(x^2+x-2\right)dx$

$=-\left(\frac{x^3}{3}+\frac{x^2}{2}-2x\right)\left|\begin{array}{c}1\\ -2\end{array}\right.$

$=\frac{9}{2}$

Câu 6: Tính diện tích hình phẳng giới hạn bởi các đường có phương trình $x=y^3,y=1$ và $x=8$

A. $\frac{17}{4}$

B. $\frac{17}{2}$

C. $\frac{17}{8}$

D. $\frac{27}{4}$

Hiển thị đáp án

Đáp án: A

Giải thích:

Tung độ giao điểm của đường cong $x=y^3$ và đường thẳng $x=8$ là nghiệm của phương trình $y^3=8\iff y=2$. Vậy diện tích cần tìm là:

$S={\int }_1^2\left|y^3-8\right|dy$

$={\int }_1^2\left(y^3-8\right)dy$

$=-\left(\frac{y^4}{4}-8y\right)\left|\begin{array}{c}2\\ 1\end{array}\right.$

$=-\left[\left(\frac{16}{4}-16\right)-\left(\frac{1}{4}-8\right)\right]$

$=\frac{17}{4}$

Câu 7: Đồ thị hai hàm số $y=\sqrt{x},y=6-x$ và trục hoành.

A. $\frac{23}{3}$

B. $\frac{22}{3}$

C. $\frac{25}{3}$

D. $\frac{29}{3}$

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có: $y=\sqrt{x}\iff x=y^2\left(y\ge 0\right);$

$y=6-x\iff x=6-y$

Tung độ giao điểm của hai đường thẳng $x=y^2,x=6-y$ là nghiệm của phương trình $y^2=6-y$ $\iff y^2+y-6=0$ $\iff \left[\begin{array}{c}y=-3\left(L\text{ vi y}\ge \text{0}\right)\\ y=2\end{array}\right.$

Vậy diện tích cần tìm là $S={\int }_0^2\left|y^2-\left(6-y\right)\right|dy$

$={\int }_0^2\left|y^2+y-6\right|dy$

$=-{\int }_0^2\left(y^2+y-6\right)dy$

$=-\left(\frac{y^3}{3}+\frac{y^2}{2}-6y\right)\left|\begin{array}{c}2\\ 0\end{array}\right.$

$=-\left(\frac{8}{3}+\frac{4}{2}-12\right)=\frac{22}{3}$

Câu 8. Tính diện tích các hình phẳng giới hạn bởi: Đồ thị các hàm số $y=4-x^2,$ $y=-x+2$

A. $\frac{9}{2}$

B. $\frac{22}{5}$

C. $\frac{11}{3}$

D. $\frac{25}{3}$

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có $4-x^2=-x+2$

$\iff x^2-x-2=0$

$\iff \left[\begin{array}{c}x=-1\\ x=2\end{array}\right.$

Vậy diện tích hình phẳng cần tìm là:

$S={\int }_{-1}^2\left|\left(-x+2\right)-\left(4-x^2\right)\right|dx$

$={\int }_{-1}^2\left|x^2-x-2\right|dx$

$=-{\int }_{-1}^2\left(x^2-x-2\right)dx$

$=-\left(\frac{x^3}{3}-\frac{x^2}{2}-2x\right)\left|\begin{array}{c}2\\ -1\end{array}\right.$

$=-\left[\left(\frac{8}{3}-\frac{4}{2}-4\right)-\left(-\frac{1}{3}-\frac{1}{2}+2\right)\right]$

$=\frac{9}{2}$

Câu 9. Cho hình phẳng (H) được giới hạn bởi đồ thị hàm số $y=\sqrt{e^x}$ và các đường thẳng $y=0$, $x=0$ và $x=2$. Thể tích V của khối tròn xoay được tạo thành khi quay hình phẳng (H) quanh trục Ox được tính bởi công thức nào sau đây?

A. $V=\pi \underset{0}{\overset{2}{\int }}{e}^x\text{d}x$.

B. $V=\pi \underset{0}{\overset{2}{\int }}{e}^{2x}\text{d}x$.

C. $V=\pi \underset{0}{\overset{2}{\int }}{e}^{x^2}\text{d}x$.

D. $V=\underset{0}{\overset{2}{\int }}{e}^{x^2}\text{d}x$.

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có: $V=\pi \underset{0}{\overset{2}{\int }}{\left(\sqrt{e^x}\right)}^2\text{d}x$

$=\pi \underset{0}{\overset{2}{\int }}{e}^x\text{d}x$.

Câu 10. Gọi (H) là hình phẳng giới hạn bởi đồ thị $y=e^x$, trục Ox và hai đường thẳng $x=0$, $x=1$. Thể tích của khối tròn xoay khi quay (H) xung quanh trục Ox là

A. $\frac{\pi }{2}\left(e^2-1\right)$.

B. $\pi \left(e^2+1\right)$.

C. $\frac{\pi }{2}\left(e^2+1\right)$.

D. $\pi \left(e^2-1\right)$.

Hiển thị đáp án

Đáp án: A

Giải thích:

$V=\pi \underset{0}{\overset{1}{\int }}{\left(e^x\right)}^2\text{dx}$

$=\pi \underset{0}{\overset{1}{\int }}{e}^{2x}\text{dx}$

$={\left.\frac{\pi }{2}{e}^{2x}\right|}_0^1$

$=\frac{\pi }{2}\left(e^2-e^0\right)$

$=\frac{\pi }{2}\left(e^2-1\right)$

Xem thêm các bài tổng hợp lý thuyết Toán lớp 12 đầy đủ, chi tiết khác:

Lý thuyết Ôn tập chương 3

Lý thuyết Số phức

Lý thuyết Cộng, trừ và nhân số phức

Lý thuyết Phép chia số phức

Lý thuyết Phương trình bậc hai với hệ số thực