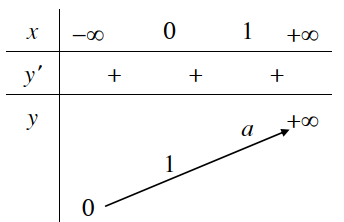Lý thuyết Hàm số mũ. Hàm số logarit (năm 2024 + Bài Tập)– Toán 12

Lý thuyết Toán 12 Bài 4: Hàm số mũ. Hàm số logarit

Bài giảng Toán 12 Bài 4: Hàm số mũ. Hàm số logarit

A. Lý thuyết

I. Hàm số mũ

1. Định nghĩa.

Cho số thực dương a khác 1.

Hàm số y = a^x được gọi là hàm số mũ cơ số a.

Ví dụ 1. Các hàm số y = 2^x; $y={\left(\frac{1}{2}\right)}^x;y={\left(\sqrt{3}\right)}^x$ là các hàm số mũ.

2. Đạo hàm của hàm số mũ

Ta thừa nhận công thức: $\underset{t\to 0}{\lim }\frac{e^t-1}{t}=1$

– Định lí 1: Hàm số y = e^x có đạo hàm tại mọi x và (e^x)’ = e^x.

– Chú ý: Công thức đạo hàm của hàm hợp đối với hàm số e^u ( với u = u(x))

là (e^u)’ = u’. e^u.

– Định lí 2: Hàm số y = a^x ( a > 0; a ≠ 1) có đạo hàm tại mọi x và: (a^x)’ = a^x. ln a

– Chú ý: Đối với hàm hợp y = a^u(x) ta có: (a^u)’ = a^u. lnu . u’

Ví dụ 2. Hàm số $y=2^{-x^2+\text{\hspace{0.17em}}2x-10}$ có đạo hàm là:

$$\begin{gathered} y\text{'}=2^{-x^2+\text{\hspace{0.17em}}2x-10}.(-x^2+\text{\hspace{0.17em}}2x-10)\text{'}.\ln 2 \\ =2^{-x^2+\text{\hspace{0.17em}}2x-10}.(-2x+\text{}2)\ln 2 \end{gathered}$$

3. Khảo sát hàm số mũ y = a^x ( a > 0 và a ≠ 1).

y = ax ; a > 1	y = ax ; 0 < a < 1
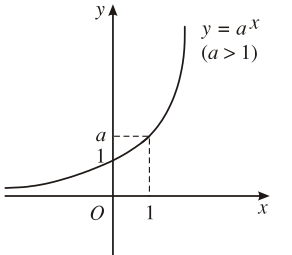
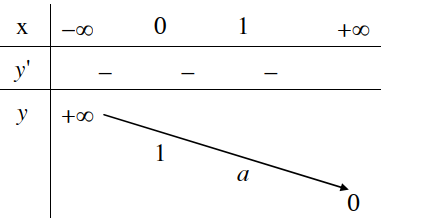
1. Tập xác định: R 2. Sự biến thiên y’ = ax.ln a > 0 với mọi x Giới hạn đặc biệt: $$\begin{gathered} \underset{x\to -\infty }{\lim }{a}^x=0; \\ \underset{x\to +\infty }{\lim }{a}^x=+\infty \end{gathered}$$ Tiệm cận: Trục Ox là tiệm cận ngang. 3. Bảng biến thiên: 4. Đồ thị	1. Tập xác định: R 2. Sự biến thiên y’ = ax.ln a < 0 với mọi x Giới hạn đặc biệt: $$\begin{gathered} \underset{x\to -\infty }{\lim }{a}^x=+\infty ; \\ \underset{x\to +\infty }{\lim }{a}^x=0 \end{gathered}$$ Tiệm cận: Trục Ox là tiệm cận ngang. 3. 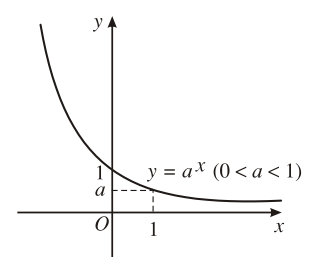Bảng biến thiên: 4. Đồ thị

Bảng tóm tắt các tính chất của hàm số mũ y = a^x ( a > 0; a ≠ 1).

Tập xác định	$\left(-\infty ;+\infty \right)$
Đạo hàm	y’ = ax. lna
Chiều biến thiên	a > 1: Hàm số luôn đồng biến. 0 < a < 1: Hàm số luôn nghịch biến
Tiệm cận	Trục Ox là tiệm cận ngang
Đồ thị	Đi qua các điểm (0; 1) và (1; a), nằm phía trên trục hoành (y = ax > 0 $\forall x\in ℝ$).

II. Hàm số logarit

1. Định nghĩa.

Cho số thực dương a khác 1.

Hàm số y = log_ax được gọi là hàm số logarit cơ số a.

Ví dụ 3. Các hàm số y = log₅ x; $y={\log }_{\frac{2}{3}}x;y={\log }_{\sqrt{3}}x$; y = ln x là các hàm số logarit với cơ số lần lượt là $5;\frac{2}{3};\sqrt{3}$ và e.

2. Đạo hàm của hàm số logarit

– Định lí 3. Hàm số y = log_a x (a > 0; a ≠ 1) có đạo hàm tại mọi x > 0 và $\left({\log }_{a}x\right)\text{'}=\frac{1}{x\ln a}$

– Đặc biệt: $\left(\ln x\right)\text{'}=\frac{1}{x}$

– Chú ý:

Đối với hàm hợp y = log_au(x); ta có: $\left({\log }_{a}u\right)\text{'}=\frac{u\text{'}}{u\ln a}$

– Ví dụ 4. Hàm số y = log₄ (x² + 2x – 7) có đạo hàm là:

$$\begin{gathered} \left({\log }_4\right(x^2+\text{\hspace{0.17em}\hspace{0.17em}}2x-7\left)\right)\text{'} \\ =\frac{(x^2+2x-7)\text{'}}{(x^2+2x-7)\ln 4} \\ =\frac{2x+2}{(x^2+2x-7)\ln 4} \end{gathered}$$

3. Khảo sát hàm số logarit y = log_a x ( a > 0; a ≠ 1).

y = loga x ; a > 1

y = logax ; 0 < a < 1

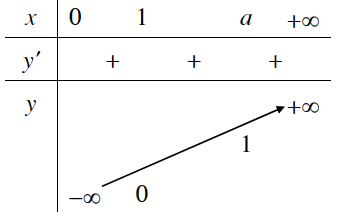
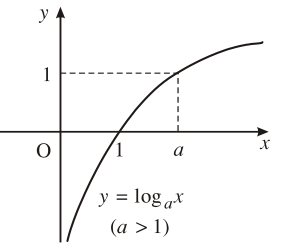
1. Tập xác định: $(0;+\text{\hspace{0.17em}}\infty )$ 2. Sự biến thiên $y\text{'}=\frac{1}{x\ln a}>\text{\hspace{0.17em}\hspace{0.17em}}0;$$\hspace{0.17em}\forall x>0$ Giới hạn đặc biệt: $\begin{array}{l}\underset{x\to 0^{+}}{\lim }{\log }_{a}x=-\infty ;\\ \underset{x\to +\infty }{\lim }{\log }_{a}x=+\infty .\end{array}$ Tiệm cận: Trục Oy là tiệm cận đứng. 3. Bảng biến thiên 4. Đồ thị

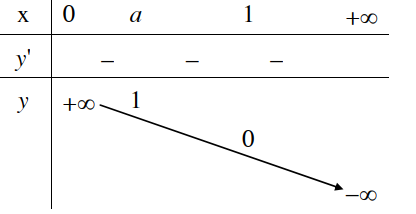
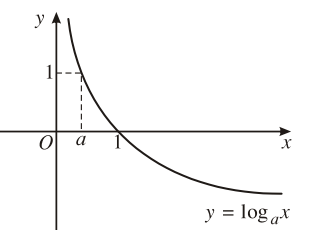
1. Tập xác định: $(0;+\text{\hspace{0.17em}}\infty )$ 2. Sự biến thiên $y\text{'}=\frac{1}{x\ln a}<\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}0;$$\hspace{0.17em}\forall x>0$ Giới hạn đặc biệt: $\begin{array}{l}\underset{x\to 0^{+}}{\lim }{\log }_{a}x=+\infty ;\\ \underset{x\to +\infty }{\lim }{\log }_{a}x=-\infty .\end{array}$ Tiệm cận: Trục Oy là tiệm cận đứng. 3. Bảng biến thiên 4. Đồ thị

Bảng tóm tắt các tính chất của hàm số y = log_ax (a > 0; a ≠ 1 ).

Tập xác định	$\left(0;+\infty \right)$
Đạo hàm	$y\text{'}=\frac{1}{x\ln a}$
Chiều biến thiên	a > 1: hàm số luôn đồng biến 0 < a< 1: hàm số luôn nghịch biến
Tiệm cận	Trục Oy là tiệm cận đứng
Đồ thị	Đi qua các điểm (1; 0) và (a; 1); nằm phía bên phải trục tung

Nhận xét:

Đồ thị của các hàm số y = a^x và y = log_a x ( a > 0; a ≠ 1) đối xứng với nhau qua đường thẳng y = x.

Bảng đạo hàm của các hàm số lũy thừa, mũ, logarit.

B. Bài tập tự luyện

Bài 1. Tính đạo hàm của các hàm số

a) y = x.e^x + 2^x

b) y = 2^x. sinx + 4^{x + 2}

c) $y=5^{(x^2+2x-3)}.x^2$

Lời giải:

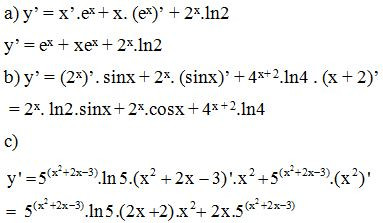
Bài 2. Tìm điều kiện xác định của các hàm số sau:

a) y = log₄ (x² – 4);

b) y = log₃ (2x – x²);

c) $y={\log }_{\sqrt{3}}\sqrt{x^2-x}$.

Lời giải:

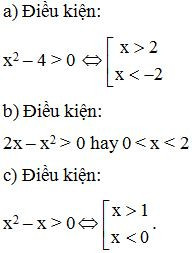
Bài 3. Tính đạo hàm của các hàm số sau:

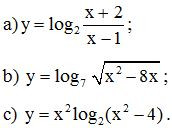
Lời giải:

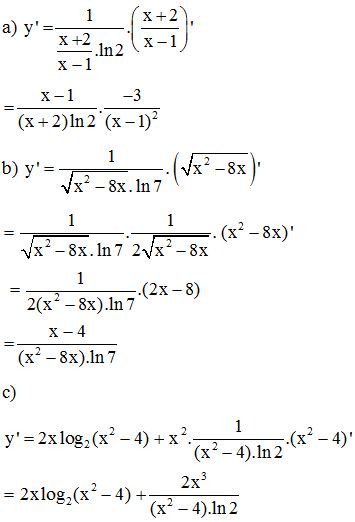
Trắc nghiệm Toán 12 Bài 4: Hàm số mũ. Hàm số Logarit

Câu 1. Tìm mệnh đề đúng trong các mệnh đề sau:

A. Đồ thị hàm số $y=a^x$ và đồ thị hàm số $y={\log }_{a}x$ đối xứng nhau qua đường thẳng y = x.

B. Hàm số $y=a^x$ với $0<a<1$ đồng biến trên khoảng $(-\infty ;+\infty )$.

C. Hàm số $y=a^x$ với $a>1$ nghịch biến trên khoảng $(-\infty ;+\infty )$.

D. Đồ thị hàm số $y=a^x$ với $a>0$ và $a\ne 1$ luôn đi qua điểm $M(a;1)$.

Hiển thị đáp án

Đáp án: A

Giải thích:

Câu B sai vì hàm số $y=a^x$ với $0<a<1$ nghịch biến trên khoảng $(-\infty ;+\infty )$.

Câu C sai vì hàm số $y=a^x$ với $a>1$ đồng biến trên khoảng $(-\infty ;+\infty )$.

Câu D sai vì đồ thị hàm số $y=a^x$ với $a>0$ và $a\ne 1$ luôn đi qua điểm $M(a;a^a)$ hoặc $M(0;1)$ chứ không phải $M(a;1)$.

Câu 2. Tập giá trị của hàm số $y=a^x(a>0;a\ne 1)$ là:

A. $(0;+\infty )$

B. $\text{[}0;+\infty )$

C. $ℝ\backslash \text{{}0\}$

D. $ℝ$

Hiển thị đáp án

Đáp án: A

Giải thích:

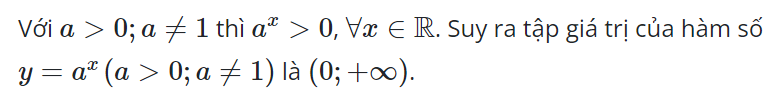
Câu 3. Với $a>0$ và $a\ne 1$. Phát biểu nào sau đây không đúng?

A. Hai hàm số $y=a^x$ và $y={\log }_{a}x$ có cùng tập giá trị.

B. Hai hàm số $y=a^x$ và $y={\log }_{a}x$ có cùng tính đơn điệu.

C. Đồ thị hai hàm số $y=a^x$ và $y={\log }_{a}x$ đối xứng nhau qua đường thẳng $y=x$.

D. Đồ thị hai hàm số $y=a^x$ và $y={\log }_{a}x$ đều có đường tiệm cận.

Hiển thị đáp án

Đáp án: A

Giải thích:

Tập giá trị của hàm số y = a^x là $\left(0;+\infty \right)$, tập giá trị của hàm số y = log_ax là $\mathrm{ℝ}$.

Câu 4. Tìm x để hàm số $y=\log \sqrt{x^2+x-12}$ có nghĩa.

A. $x\in (-\infty ;-4)\cup (3;+\infty )$

B. $x\in (-4;3)$

C. $\left\{\begin{array}{l}x\ne -4\\ x\ne 3\end{array}\right.$

D. $x\in R$.

Hiển thị đáp án

Đáp án: A

Giải thích:

Hàm số $\log \sqrt{x^2+x-12}$ có nghĩa khi $x^2+x-12>0$

$\iff [\begin{array}{c}x>3\\ x<-4\end{array}$

Câu 5. Tập xác định của hàm số $y={\log }_2\frac{x+3}{2-x}$ là:

A. $D=(-3;2)$

B. $D=ℝ\backslash \text{{}-\text{3};2\}$

C. $D=(-\infty ;-3)\cup (2;+\infty )$

D. $D=\text{[}-\text{3};2]$

Hiển thị đáp án

Đáp án: A

Giải thích:

Hàm số ${\log }_2\frac{x+3}{2-x}$ có nghĩa khi $\frac{x+3}{2-x}>0$

$\iff -3<x<2$

Câu 6. Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

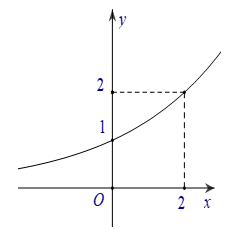
A. $y={\left(\sqrt{2}\right)}^x$

B. $y=x$

C. $y=2^x$

D. $y={\left(\sqrt{2}\right)}^{-x}$

Hiển thị đáp án

Đáp án: A

Giải thích:

Nhận thấy đây là đồ thị hàm số dạng $y=a^x$. Ta có $A(0;1)$ và $B(2;2)$ thuộc đồ thị hàm số.

Suy ra, $\left\{\begin{array}{l}{a}^0=1\\ a^2=2\\ a>0\end{array}\right.\Rightarrow a=\sqrt{2}$ . Hàm số là $y={\left(\sqrt{2}\right)}^x$.

Câu 7. Đạo hàm của hàm số $y=\sin x+{\log }_3{x}^3(x>0)$ là:

A. $y\text{'}=\cos x+\frac{3}{x\ln 3}$

B. $y\text{'}=-\cos x+\frac{3}{x\ln 3}$

C. $y\text{'}=\cos x+\frac{1}{x^3\ln 3}$

D. $y\text{'}=-\cos x+\frac{1}{x^3\ln 3}$

Hiển thị đáp án

Đáp án: A

Giải thích:

$y=\sin x+{\log }_3{x}^3$

$\Rightarrow y\text{'}=\cos \text{x}+\frac{3{\text{x}}^2}{x^3\ln 3}$

$=\cos \text{x}+\frac{3}{x\ln 3}$

Câu 8. Cho hàm số $f\left(x\right)=\ln \left(x^4+1\right)$. Đạo hàm $f^{/}\left(0\right)$ bằng:

A. 1

B. 2

C. 3

D. 4

Hiển thị đáp án

Đáp án: A

Giải thích:

$f\left(x\right)=\ln (x^4+1)$

$\Rightarrow f\text{'}\left(x\right)=\frac{(x^4+1)\text{'}}{x^4+1}$

$=\frac{4{\text{x}}^3}{x^4+1}$

$\Rightarrow f\text{'}\left(0\right)=0$

Câu 9. Cho hàm số $f\left(x\right)=x{e}^x$. Gọi ${f^{/}}^{/}\left(x\right)$ là đạo hàm cấp hai của $f\left(x\right)$. Ta có ${f^{/}}^{/}\left(1\right)$ bằng:

A. $3e$

B. $-3e^2$

C. $e^3$

D. $-5e^2$

Hiển thị đáp án

Đáp án: A

Giải thích:

$f\left(x\right)=x.e^x$

$\Rightarrow f\text{'}\left(x\right)=e^x+x.e^x$

$\Rightarrow f\text{'}\text{'}\left(x\right)=e^x+e^x+x.e^x$

$\Rightarrow f\text{'}\text{'}\left(1\right)=3\text{e}$

Câu 10. Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

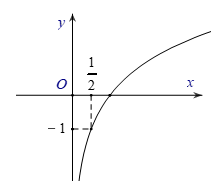
A. $y={\log }_{2}x$

B. $y={\log }_{\frac{1}{2}}x$

C. $y={\log }_{\sqrt{2}}x$

D. $y={\log }_2\left(2x\right)$

Hiển thị đáp án

Đáp án: A

Giải thích:

Nhận thấy đây là đồ thị hàm số $y={\log }_{a}x$. Điểm $\left(\frac{1}{2};-1\right)$ thuộc đồ thị hàm số nên $-1={\log }_a\frac{1}{2}$ $\Rightarrow a^{-1}=\frac{1}{2}$ $\Rightarrow \frac{1}{a}=\frac{1}{2}\Rightarrow a=2$ .

Hàm số là $y={\log }_{2}x$.

Xem thêm các bài tổng hợp lý thuyết Toán lớp 12 đầy đủ, chi tiết khác:

Lý thuyết Phương trình mũ và phương trình logarit

Lý thuyết Bất phương trình mũ và bất phương trình logarit

Lý thuyết Ôn tập chương 2

Lý thuyết Nguyên hàm

Lý thuyết Tích phân