Lý thuyết Ôn tập chương 3 (mới 2024 + Bài Tập) – Toán 12

Lý thuyết Toán 12 Ôn tập chương 3

A. Lý thuyết

1. Nguyên hàm và tính chất

1.1 Nguyên hàm.

- Định nghĩa

Cho hàm số f(x) xác định trên K (K là khoảng, đoạn hay nửa khoảng của R).

Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F’(x) = f(x) với mọi $x\in K$.

Ví dụ.

- Hàm số F(x) = sinx + 6 là một nguyên hàm của hàm số f(x) = cosx trên khoảng $\left(-\infty ;+\infty \right)$ vì F’(x) = (sinx + 6)’ = cosx với $\forall x\in \left(-\infty ;+\infty \right)$.

- Hàm số $F\left(x\right)=\frac{x+\text{\hspace{0.17em}}2}{x-3}$ là một nguyên hàm của hàm số $f\left(x\right)=\frac{-5}{{(x-3)}^2}$ trên khoảng $(-\infty ;3)\cup (3;+\text{\hspace{0.17em}}\infty )$

Vì $F\text{'}\left(x\right)={\left(\frac{x+\text{\hspace{0.17em}}2}{x-3}\right)}^{\text{'}}$$=\frac{-5}{{(x-3)}^2}=f\left(x\right)$ với $\forall x\in (-\infty ;3)\cup (3;+\infty )$

- Định lí 1.

Nếu F(x) là một nguyên hàm của f(x) trên K thì với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x) trên K.

- Định lí 2.

Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C, với C là một hằng số.

Do đó $F\left(x\right)+C;C\in ℝ$ là họ tất cả các nguyên hàm của f(x) trên K.

Kí hiệu: $\underset{}{\overset{}{\int }}f\left(x\right)\text{}dx=F\left(x\right)+C$

- Chú ý: Biểu thức f(x)dx chính là vi phân của nguyên hàm F(x) của f(x), vì dF(x) = F’(x)dx = f(x)dx.

Ví dụ.

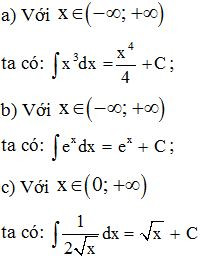
1.2 Tính chất của nguyên hàm

Ví dụ. Tìm nguyên hàm của hàm số $f\left(x\right)=3x^2+\text{\hspace{0.17em}\hspace{0.17em}}2\sin x$ trên khoảng $\left(-\infty ;+\infty \right)$.

Lời giải:

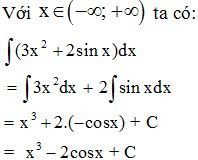
1.3 Sự tồn tại nguyên hàm

Định lí:

Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K.

Ví dụ.

a) Hàm số $y=\sqrt{x}$ có nguyên hàm trên khoảng $\left(0;+\infty \right)$.

$\int \sqrt{x}dx=\int x^{\frac{1}{2}}dx$$=\frac{2}{3}{x}^{\frac{3}{2}}+C=\frac{2}{3}x\sqrt{x}+C$

b) Hàm số y = $\frac{1}{x}$ có nguyên hàm trên khoảng $\left(-\infty ;0\right)\cup \left(0;+\infty \right)$

$\int \frac{1}{x}dx=\ln \left|x\right|+\text{\hspace{0.17em}\hspace{0.17em}}C$

1.4 Bảng nguyên hàm của một số hàm số thường gặp

Ví dụ. Tính:

a) $\int \left(3x^4+\text{\hspace{0.17em}\hspace{0.17em}}\sqrt[3]{x}\right)dx$

b) $\int (5e^x-4^{x+\text{\hspace{0.17em}}2})dx$

Lời giải:

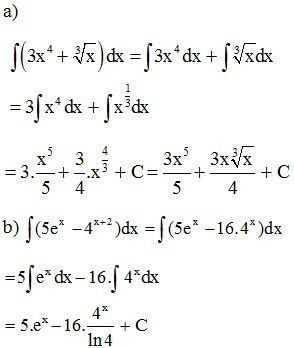
- Chú ý: Từ đây, yêu cầu tìm nguyên hàm của một hàm số được hiểu là tìm nguyên hàm trên từng khoảng xác định của nó.

2. Phương pháp tính nguyên hàm.

2.1 Phương pháp đổi biến số

- Định lí 1.

Nếu $\int f\left(u\right)du=F\left(u\right)+\text{\hspace{0.17em}\hspace{0.17em}}C$ và u = u(x) là hàm số có đạo hàm liên tục thì:

$\int f\left(u\right(x\left)\right).u\text{'}\left(x\right)dx$$=F\left(u\right(x\left)\right)+C$

Hệ quả: Nếu u = ax + b (a ≠ 0), ta có:

$\int f(ax+\text{\hspace{0.17em}}b)dx$$\hspace{0.17em}=\frac{1}{a}F(ax+\text{\hspace{0.17em}}b)+\text{\hspace{0.17em}}C$

Ví dụ. Tính $\int {(3x+\text{\hspace{0.17em}}2)}^{3}dx$.

Lời giải:

Ta có: $\int u^{3}du=\frac{u^4}{4}+\text{\hspace{0.17em}}C$ nên theo hệ quả ta có:

$\int {(3x+\text{\hspace{0.17em}}2)}^{3}dx$$\hspace{0.17em}=\frac{{(3x+2)}^4}{4}+\text{\hspace{0.17em}\hspace{0.17em}}C$

Chú ý:

Nếu tính nguyên hàm theo biến mới u (u = u(x)) thì sau khi tính nguyên hàm, ta phải trở lại biến x ban đầu bằng cách thay u bởi u(x).

Ví dụ. Tính $\int \sin x.c{\text{os}}^{2}xdx$.

Lời giải:

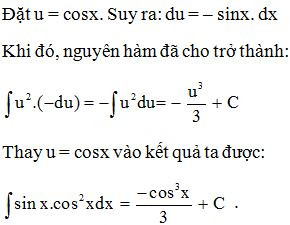
2.2 Phương pháp tính nguyên hàm từng phần.

- Định lí 2.

Nếu hai hàm số u = u(x) và v = v(x) có đạo hàm liên tục trên K thì:

$\int u\left(x\right).v\text{'}\left(x\right).dx$$=u\left(x\right).v\left(x\right)-\int u\text{'}\left(x\right).v\left(x\right)dx$

- Chú ý.

Vì u’(x) dx = du; v’(x) dx = dv. Nên đẳng thức trên còn được viết ở dạng:

$\int udv=uv-\int vdu$

Đó là công thức nguyên hàm từng phần.

Ví dụ. Tính

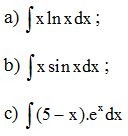
Lời giải:

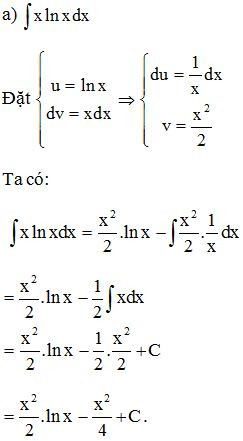
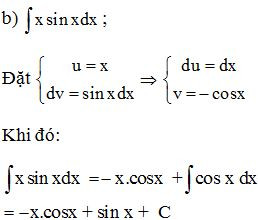
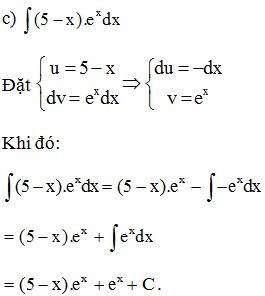
3. Khái niệm tích phân

3.1 Diện tích hình thang cong

- Cho hàm số y = f(x) liên tục, không đổi dấu trên đoạn [a; b]. Hình phẳng giới hạn bởi đồ thị của hàm số y = f(x), trục hoành và hai đường thẳng x = a; x = b được gọi là hình thang cong.

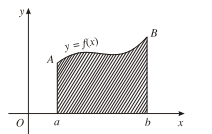
- Ta xét bài toán tìm diện tích hình thang cong bất kì:

Cho hình thang cong giới hạn bởi các đường thẳng x = a; x = b (a < b); trục hoành và đường cong y = f(x), trong đó f(x) là hàm số liên tục, không âm trên đoạn [a; b].

Với mỗi $x\in \left[a;b\right]$, kí hiệu S(x) là diện tích của phần hình thang cong đó nằm giữa hai đường thẳng vuông góc với Ox lần lượt tại a và b.

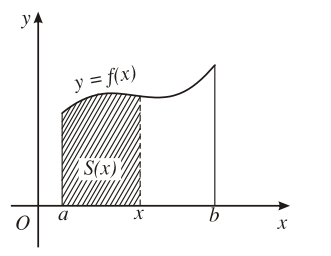
Ta chứng minh được S(x) là một nguyên hàm của f(x) trên đoạn [a; b].

Giả sử F(x) cũng là một nguyên hàm của f(x) thì có một hằng số C sao cho S(x) = F(x) + C.

Vì S(a) = 0 nên F(a) + C = 0 hay C = – F(a).

Vậy S(x) = F(x) – F(a).

Thay x = b vào đẳng thức trên, ta có diện tích của hình thang cần tìm là:

S(b) = F(b) – F(a).

3.2 Định nghĩa tích phân

Cho f(x) là hàm số liên tục trên đoạn [a; b]. Giả sử F(x) là một nguyên hàm của f(x) trên đoạn [a; b].

Hiệu số F(b) – F(a) được gọi là tích phân từ a đến b (hay tích phân xác định trên đoạn [a; b]) của hàm số f(x), kí hiệu $\underset{a}{\overset{b}{\int }}f\left(x\right)dx$.

Ta còn dùng kí hiệu để chỉ hiệu số F(b) – F(a).

Vậy $\underset{a}{\overset{b}{\int }}f\left(x\right)dx$$=F{\left(x\right)}_a^b=F\left(b\right)-F\left(a\right)$

Ta gọi $\underset{a}{\overset{b}{\int }}$ là dấu tích phân, a là cận dưới, b là cận trên, f(x)dx là biểu thức dưới dấu tích phân và f(x) là hàm số dưới dấu tích phân.

- Chú ý.

Trong trường hợp a = b hoặc a > b, ta quy ước:

$\underset{a}{\overset{a}{\int }}f\left(x\right)dx=0;$$\underset{a}{\overset{b}{\int }}f\left(x\right)\text{}dx=-\underset{b}{\overset{a}{\int }}f\left(x\right)\text{}dx$

Ví dụ.

a) $\underset{0}{\overset{2}{\int }}(x+\text{}2)dx$

$$\begin{gathered} ={\left.\left(\frac{x^2}{2}+2x\right)\right|}_0^2 \\ =6-0=6 \end{gathered}$$

b) $\underset{0}{\overset{\frac{\pi }{2}}{\int }}(2+\text{\hspace{0.17em}}\cos x)dx$

$$\begin{gathered} ={\left.\left(2x+\text{\hspace{0.17em}\hspace{0.17em}}\sin x\right)\right|}_0^{\frac{\pi }{2}} \\ =(\pi +1)-0 \\ =\mathrm{\pi }+1 \end{gathered}$$

- Nhận xét.

a) Tích phân của hàm số f từ a đến b có thể kí hiệu là $\underset{a}{\overset{b}{\int }}f\left(x\right)dx$ hay $\underset{a}{\overset{b}{\int }}f\left(t\right)dt$. Tích phân đó chỉ phụ thuộc vào f và các cận a, b mà không phụ thuộc vào biến x hay t.

b) Ý nghĩa hình học của tích phân.

Nếu hàm số f(x) liên tục và không âm trên đoạn [a; b] thì tích phân $\underset{a}{\overset{b}{\int }}f\left(x\right)dx$ là diện tích S của hình thang cong giới hạn bởi đồ thị của f(x), trục Ox và hai đường thẳng x = a; x = b. Vậy $S\text{\hspace{0.17em}}=\underset{a}{\overset{b}{\int }}f\left(x\right)dx$.

4. Tính chất của tích phân.

Ví dụ. Tính: $\underset{0}{\overset{\pi }{\int }}(3x-4\sin x)dx$.

Lời giải:

Ta có:

$\begin{array}{l}\underset{0}{\overset{\pi }{\int }}(3x-4\sin x)dx\\ =3\underset{0}{\overset{\pi }{\int }}xdx-4\underset{0}{\overset{\pi }{\int }}\sin xdx\\ =3{\left..\frac{x^2}{2}\right|}_0^{\pi }+\text{}{\left.4c\text{os x}\right|}_0^{\pi }\\ =\frac{3{\pi }^2}{2}+\text{\hspace{0.17em}}(-4-4)=\frac{3{\pi }^2}{2}-8\end{array}$

- Tính chất 3.

$\underset{a}{\overset{b}{\int }}f\left(x\right)dx$$=\underset{a}{\overset{c}{\int }}f\left(x\right)dx+\underset{c}{\overset{b}{\int }}f\left(x\right)dx$ (a < c < b).

Ví dụ. Tính $\underset{-2}{\overset{2}{\int }}\left|x\right|dx$.

Lời giải:

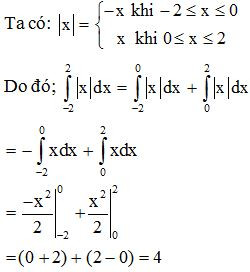
5. Phương pháp tính tích phân

5.1 Phương pháp đổi biến số

- Định lí:

Cho hàm số f(x) liên tục trên đoạn [a; b]. Giả sử hàm số $x=\phi \left(t\right)$ có đạo hàm liên tục trên đoạn $\left[\alpha ;\beta \right]$ sao cho $\phi \left(\alpha \right)=a;\phi \left(\beta \right)=b$ và $a\le \phi \left(t\right)\le b\forall t\in \left[\alpha ;\beta \right]$.

Khi đó: $\underset{a}{\overset{b}{\int }}f\left(x\right)\text{}dx$$\hspace{0.17em}=\underset{\alpha }{\overset{\beta }{\int }}f\left(\phi \left(t\right)\right).\phi \text{'}\left(t\right)dt$

Ví dụ. Tính $\underset{0}{\overset{1}{\int }}\sqrt{1-x^2}dx$.

Lời giải:

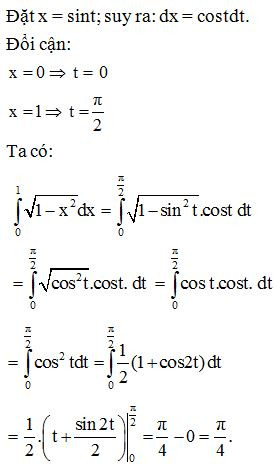
- Chú ý:

Trong nhiều trường hợp ta còn sử dụng phép đổi biến số ở dạng sau:

Cho hàm số f(x) liên tục trên đoạn [a; b]. Để tính $\underset{a}{\overset{b}{\int }}f\left(x\right)dx$, đôi khi ta chọn hàm số u = u(x) làm biến số mới, trong đó trên đoạn [a; b], u(x) có đạo hàm liên tục và $u\left(x\right)\in \left[\alpha ;\beta \right]$.

Giả sử có thể viết: f(x) = g(u(x)). u’(x) với $x\in \left[a;b\right]$ với g(u) liên tục trên đoạn $\left[\alpha ;\beta \right]$

Khi đó, ta có: $\underset{a}{\overset{b}{\int }}f\left(x\right)dx$$=\underset{u\left(a\right)}{\overset{u\left(b\right)}{\int }}g\left(u\right)du$

Ví dụ. Tính $\underset{0}{\overset{\sqrt{\pi }}{\int }}x.\sin x^{2}dx$.

Lời giải:

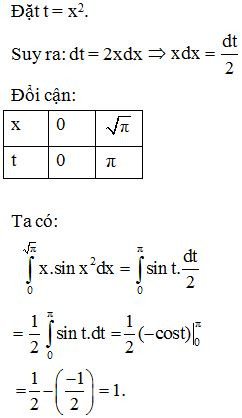
5.2 Phương pháp tính tích phân từng phần

- Định lí.

Nếu u = u(x) và v = v(x) là hai hàm số có đạo hàm liên tục trên đoạn [a; b] thì:

$\underset{a}{\overset{b}{\int }}u\left(x\right).v\text{'}\left(x\right)dx$$\hspace{0.17em}={\left[u\left(x\right).v\left(x\right)\right]}_a^b$$-\underset{a}{\overset{b}{\int }}v\left(x\right).u\text{'}\left(x\right)dx$

Hay $\underset{a}{\overset{b}{\int }}udv={\left.uv\right|}_a^b-\underset{a}{\overset{b}{\int }}vdu$

Ví dụ. Tính $I=\underset{0}{\overset{\frac{\pi }{2}}{\int }}x\sin xdx.$

Lời giải:

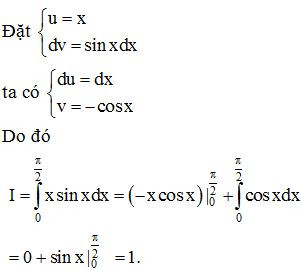
Ví dụ. Tính $I=\underset{0}{\overset{e-1}{\int }}x\ln (x+1)dx$.

Lời giải:

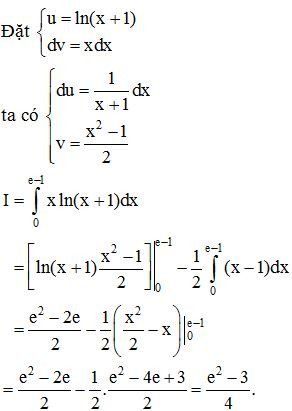
6. Tính diện tích hình phẳng

6.1 Hình phẳng giới hạn bởi một đường cong và trục hoành

Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) liên tục trên đoạn [a; b], trục hoành và hai đường thẳng x = a; x = b được xác định: $S\text{\hspace{0.17em}\hspace{0.17em}}=\underset{a}{\overset{b}{\int }}\left|f\left(x\right)\right|dx$.

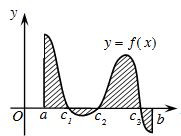
Ví dụ. Tính diện tích hình phẳng được giới hạn bởi y = 5x⁴ + 3x², trục hoành và hai đường thẳng x = 0; x = 1.

Lời giải:

Diện tích hình phẳng cần tính là:

$\begin{array}{l}S=\underset{0}{\overset{1}{\int }}\left|5x^4+3x^2\right|dx\\ =\underset{0}{\overset{1}{\int }}\left(5x^4+3x^2\right)dx\\ ={\left.\left(x^5+\text{\hspace{0.17em}}{x}^3\right)\right|}_0^1=2\end{array}$

6.2 Hình phẳng được giới hạn bởi 2 đường cong

Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x); y = g(x) liên tục trên đoạn [a; b] và hai đường thẳng x = a; x = b được xác định:

$S\text{\hspace{0.17em}\hspace{0.17em}}=\underset{a}{\overset{b}{\int }}\left|f\left(x\right)-g\left(x\right)\right|dx$(*).

- Chú ý.

Khi áp dụng công thức (*), cần khử dấu giá trị tuyệt đối của hàm số dưới dấu tích phân. Muốn vậy ta giải phương trình: f(x) – g(x) = 0 trên đoạn [a; b].

Giả sử phương trình có hai nghiệm c; d (c < d). Khi đó, f(x) – g(x) không đổi dấu trên các đoạn [a; c]; [c; d]; [d; b]. Trên mỗi đoạn đó, chẳng hạn trên [a; c] ta có:

$\underset{a}{\overset{c}{\int }}\left|f\left(x\right)-g\left(x\right)\right|dx$$\hspace{0.17em}=\left|\underset{a}{\overset{c}{\int }}\left[f\left(x\right)-g\left(x\right)\right]dx\right|$

Ví dụ. Tính diện tích hình phẳng được giới hạn bởi các đường thẳng x = 0; x = 2 và các đồ thị của hai hàm số y = x – 1 và y = x² – 1.

Lời giải:

Phương trình hoành độ giao điểm của hai đường cong:

7. Tính thể tích

7.1 Thể tích của vật thể

Cắt một vật thể (H) bởi hai mặt phẳng (P) và (Q) vuông góc với trục Ox lần lượt tại x = a; x = b (a < b) . Một mặt phẳng tùy ý vuông góc với Ox tại điểm x $(a\le x\le b)$ cắt (H) theo thiết diện có diện tích là S(x). Giả sử S(x) liên tục trên đoạn [a; b].

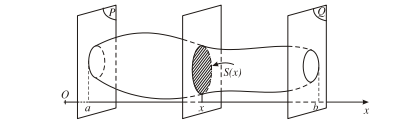
Khi đó, thể tích V của phần vật thể giới hạn bởi hai mặt phẳng (P) và (Q) được xác định bởi công thức: $V=\underset{a}{\overset{b}{\int }}S\left(x\right)dx$.

7.2 Thể tích khối chóp và khối chóp cụt.

a) Cho khối chóp có diện tích đáy là B, chiều cao h.

Khi đó, thể tích của khối chóp là $V=\frac{1}{3}B.h$.

b) Cho khối chóp cụt tạo bởi khối chóp đỉnh S có diện tích hai đáy lần lượt là B; B’ và chiều cao là h.

Thể tích của khối chóp cụt là:

$V=\frac{h}{3}\left(B+\sqrt{B.B\text{'}}+B\text{'}\right)$

8. Thể tích khối tròn xoay

- Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường cong y = f(x), trục hoành và hai đường thẳng x = a; x = b quanh trục Ox:

$V=\pi \underset{a}{\overset{b}{\int }}{f}^2\left(x\right)dx$

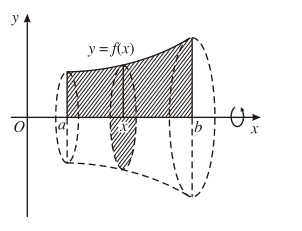
Ví dụ. Cho hình phẳng giới hạn bởi đường cong , trục hoành và hai đường thẳng x = 0; x = 2. Tính thể tích khối tròn xoay thu được khi quay hình này quanh trục Ox.

Lời giải:

Thể tích khối tròn xoay cần tính là:

$V=\pi \underset{0}{\overset{2}{\int }}{x}^{4}dx$$=\pi {\left.\frac{x^5}{5}\right|}_0^2=\frac{32\pi }{5}$

B. Bài tập tự luyện

Bài 1. Trong các cặp hàm số sau, hàm số nào là một nguyên hàm của hàm số còn lại.

a) x³ và $\frac{x^4}{4}+\text{\hspace{0.17em}\hspace{0.17em}}10$;

b) e^–2x + 2 và – 2e^–2x.

Lời giải:

a) Ta có:

$$\begin{gathered} {\left(\frac{x^4}{4}+\text{\hspace{0.17em}\hspace{0.17em}}10\right)}^{\text{'}} \\ ={\left(\frac{x^4}{4}\right)}^{\text{'}}+\text{\hspace{0.17em}}{10}^{\text{'}}=x^3 \end{gathered}$$

Do đó, F(x) = $\frac{x^4}{4}+\text{\hspace{0.17em}\hspace{0.17em}}10$ là một nguyên hàm của hàm số f(x) = x³.

b) Ta có: (e^–2x + 2)’ = – 2e^–2x nên F(x) = e^–2x + 2 là một nguyên hàm của hàm số

f(x) = – 2e^–2x.

Bài 2. Tìm nguyên hàm của các hàm số sau:

a) $f\left(x\right)=2x+\text{\hspace{0.17em}}{e}^{x+\text{\hspace{0.17em}}2}$;

b) f(x) = sinx + cosx.

Lời giải:

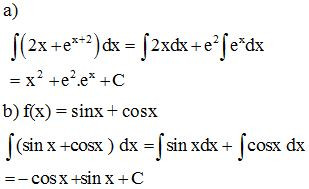
Bài 3. Sử dụng phương pháp đổi biến, tính:

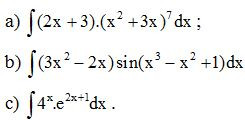
Lời giải:

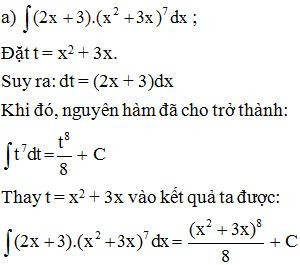
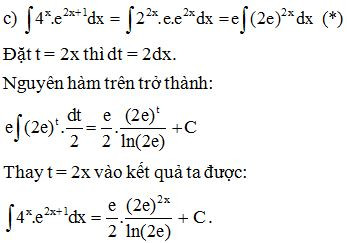
Bài 4. Sử dụng phương pháp tính nguyên hàm từng phần, tính:

a) $\int (x+\text{\hspace{0.17em}}2).\sin xdx$;

b) $\int (x+\text{\hspace{0.17em}}1).\ln xdx$.

Lời giải:

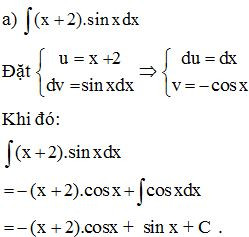
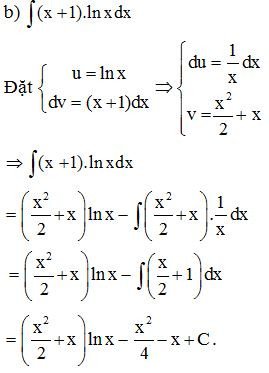
Bài 5. Tính các tích phân sau:

a) $\underset{1}{\overset{2}{\int }}\frac{x^2+4x}{x}dx$;

b) $\underset{-\frac{\pi }{2}}{\overset{\frac{\pi }{3}}{\int }}\left|\sin x\right|dx$.

Lời giải:

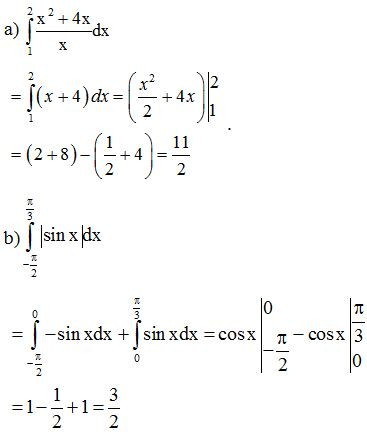
Bài 6. Sử dụng phương pháp đổi biến, hãy tính:

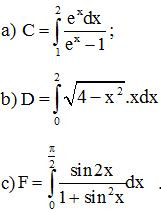
Lời giải:

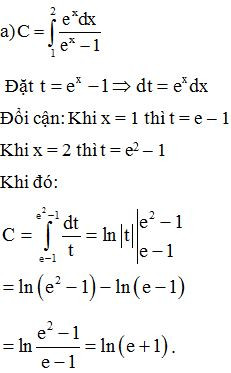
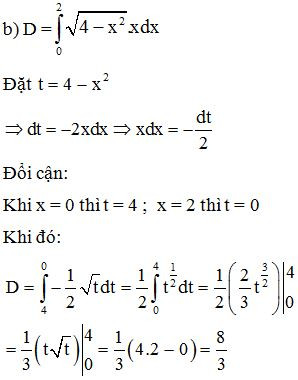
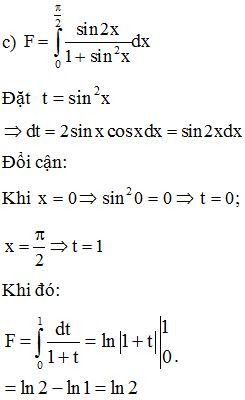
Bài 7. Sử dụng phương pháp tính tích phân từng phần, hãy tính:

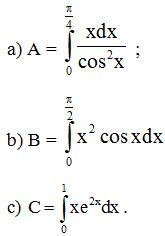
Lời giải:

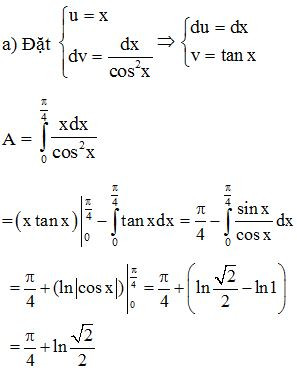
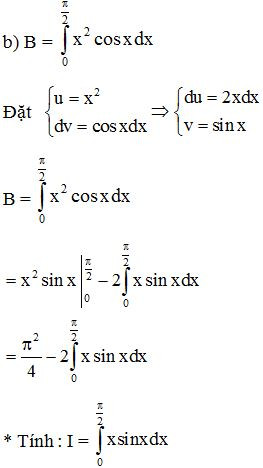
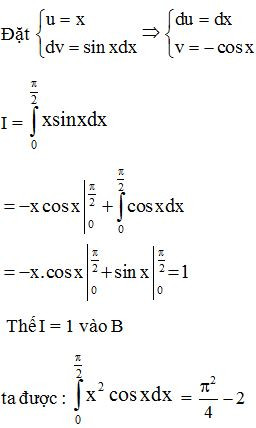
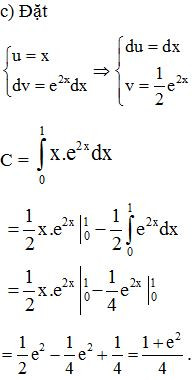
Bài 8. Tính diện tích hình phẳng giới hạn bởi các đường sau:

a) y = x³ – 3x² , trục hoành và hai đường thẳng x = 1; x = 4;

b) y = 2 – x²; y = –x.

Lời giải:

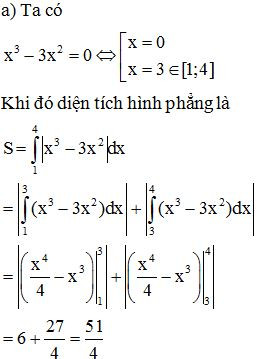
b) Phương trình hoành độ giao điểm của hai đồ thị :

Bài 9. Tính diện tích hình phẳng giới hạn bởi parabol (P): y = x² + 3, tiếp tuyến của (P) tại điểm có hoành độ x = 2 và trục tung?

Lời giải:

Ta có: y’ = 2x .

Suy ra: y’(2) = 4 và y(2) = 7.

Phương trình tiếp tuyến của (P) tại điểm có hoành độ x = 2 là

y = 4(x – 2) + 7 = 4x – 1 .

Xét phương trình hoành độ giao điểm của (P) và tiếp tuyến:

x² + 3 = 4x – 1x² – 4x + 4 = 0

$\iff$x = 2

Diện tích hình phẳng cần tính là:

$\begin{array}{l}S=\underset{0}{\overset{2}{\int }}\left|x^2+\text{\hspace{0.17em}}3-(4x-1)\right|dx\\ =\underset{0}{\overset{2}{\int }}\left|x^2-4x+\text{}4\right|dx\\ =\underset{0}{\overset{2}{\int }}\left(x^2-4x+\text{}4\right)dx\\ ={\left.\left(\frac{x^3}{3}-2x^2+\text{\hspace{0.17em}\hspace{0.17em}}4x\right)\right|}_0^2=\frac{8}{3}\end{array}$

Bài 10. Tính thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường sau quay quanh Ox.

a) y = x³ + 1; y = 0; x = 0; x = 1;

b) y = –x² + 2x ; y = 0.

Lời giải:

a) Theo công thức ta có thể tích của khối tròn xoay cần tính là:

$\begin{array}{l}V=\pi \underset{0}{\overset{1}{\int }}{(x^3+1)}^{2}dx\\ =\pi \underset{0}{\overset{1}{\int }}\left(x^6+2x^3+1\right)dx\\ =\pi {\left(\frac{x^7}{7}+\frac{x^4}{2}+\text{}x\right)}_0^1=\frac{23\pi }{14}.\end{array}$

b) Phương trình hoành độ giao điểm của hai đồ thị là:

– x² + 2x = 0$\iff \left[\begin{array}{c}x=0\\ x=2\end{array}\right.$

Theo công thức ta có thể tích của khối tròn xoay cần tính là:

$\begin{array}{l}V=\pi \underset{0}{\overset{2}{\int }}{(-x^2+2x)}^{2}dx.\\ =\pi \underset{0}{\overset{2}{\int }}(x^4+4x^2-4x^3)dx\\ =\pi {\left.\left(\frac{x^5}{5}\text{\hspace{0.17em}\hspace{0.17em}}+\frac{4x^3}{3}-x^4\right)\right|}_0^2=\frac{16\pi }{15}\end{array}$

Trắc nghiệm Toán 12 Bài: Ôn tập Chương 3 - Nguyên hàm - Tích phân và ứng dụng

Câu 1. Cho $F\left(x\right)$ là một nguyên hàm của hàm số $f\left(x\right)=\frac{\sin 2x}{1+\cos x}$ thỏa mãn $F\left(\frac{\pi }{2}\right)=0$. Tính $F\left(0\right)$.

A. $F\left(0\right)=2\ln 2+2$.

B. $F\left(0\right)=2\ln 2$.

C. $F\left(0\right)=\ln 2$.

D. $F\left(0\right)=2\ln 2-2$.

Hiển thị đáp án

Đáp án: D

Giải thích:

$f\left(x\right)=\frac{\sin 2x}{1+\cos x}$

$=\frac{2\sin x.\cos x}{1+\cos x}$

Đặt $u=1+\cos x$$\Rightarrow \text{d}u=-\sin x\text{d}x$ và $\cos x=u-1$.

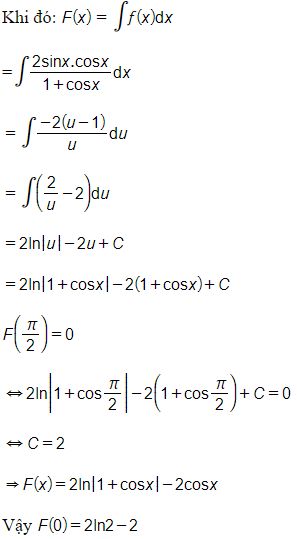
Câu 2. Tìm nguyên hàm của hàm số $f\left(x\right)=(x+1).\sin 2x$.

Hiển thị đáp án

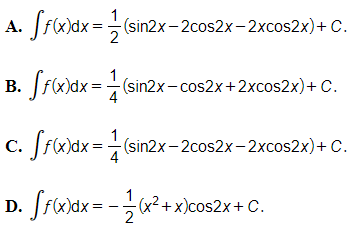
Đáp án: C

Giải thích:

Đặt $\left\{\begin{array}{l}u=x+1\\ \text{d}v=\sin 2x\text{d}x\end{array}\right.$

$\Rightarrow \left\{\begin{array}{l}\text{d}u=\text{d}x\\ v=-\frac{1}{2}\text{cos2}x\end{array}\right.$

Khi đó:

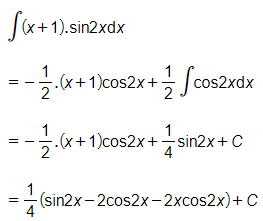
Câu 3. Cho hàm số $f\left(x\right)$ có $\underset{0}{\overset{9}{\int }}f\left(x\right)dx=9$. Tính $\underset{0}{\overset{3}{\int }}f\left(3x\right)dx$.

A. $\underset{0}{\overset{3}{\int }}f\left(3x\right)dx=3$.

B. $\underset{0}{\overset{3}{\int }}f\left(3x\right)dx=27$.

C. $\underset{0}{\overset{3}{\int }}f\left(3x\right)dx=-3$.

D. $\underset{0}{\overset{3}{\int }}f\left(3x\right)dx=1$.

Hiển thị đáp án

Đáp án: A

Giải thích:

Đặt $t=3x$ $\Rightarrow dt=3dx$

$\Rightarrow dx=\frac{1}{3}dt$.

Đổi cận $x=0\Rightarrow t=0$

$x=3\Rightarrow t=9$

$\Rightarrow \underset{0}{\overset{3}{\int }}f\left(3x\right)dx=\frac{1}{3}\underset{0}{\overset{9}{\int }}f\left(t\right)dt$

$=\frac{1}{3}\underset{0}{\overset{9}{\int }}f\left(x\right)dx=3$

Câu 4. Trong các khẳng định sau, khẳng định nào sai?

A. $\int \frac{\text{d}x}{x}=\ln x+C$.

B. $\int x^{\alpha }\text{d}x=\frac{x^{\alpha +1}}{\alpha +1}+C,\alpha \ne -1$.

C. $\int a^x\text{d}x=\frac{a^x}{\ln a}+C$.

D. $\int \frac{1}{{\cos }^{2}x}\text{d}x=\tan x+C$.

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có $\int \frac{dx}{x}=\ln \left|x\right|+C$ nên đáp án A sai.

Câu 5. Tính $I=\int 2x\sqrt{x^2+1}\text{d}x$ bằng cách đặt $u=\sqrt{x^2+1}$, mệnh đề nào dưới đây đúng?

A. $I=2\int \sqrt{u}\text{d}u$.

B. $I=\int u\text{d}u$.

C. $I=\int u^2\text{d}u$.

D. $I=2\int u^2\text{d}u$.

Hiển thị đáp án

Đáp án: D

Giải thích:

Đặt $u=\sqrt{x^2+1}$

$\Rightarrow u^2=x^2+1$

$\Rightarrow 2u\text{d}u=2x\text{d}x$.

$\Rightarrow I=\int 2u.u.\text{d}u$

$=2\int u^2\text{d}u$

Câu 6. Cho $I=\underset{0}{\overset{3}{\int }}|x-2|\text{d}x$. Khẳng định nào sau đây đúng?

A. $I=\left|\underset{0}{\overset{3}{\int }}\left(x-2\right)\text{d}x\right|$.

B. $I=-\underset{0}{\overset{2}{\int }}\left(x-2\right)\text{d}x+\underset{2}{\overset{3}{\int }}\left(x-2\right)\text{d}x$.

C. $I=\underset{0}{\overset{2}{\int }}\left(x-2\right)\text{d}x+\underset{2}{\overset{3}{\int }}\left(x-2\right)\text{d}x$.

D. $I=\underset{0}{\overset{2}{\int }}\left(x-2\right)\text{d}x-\underset{2}{\overset{3}{\int }}\left(x-2\right)\text{d}x$.

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có: $\left|x-2\right|=\left\{\begin{array}{l}x-2,x\ge 2\\ -\left(x-2\right),x<2\end{array}\right.$

Suy ra: $I=\underset{0}{\overset{3}{\int }}|x-2|\text{d}x$

$=-\underset{0}{\overset{2}{\int }}\left(x-2\right)\text{d}x+\underset{2}{\overset{3}{\int }}\left(x-2\right)\text{d}x$.

Vậy $I=-\underset{0}{\overset{2}{\int }}\left(x-2\right)\text{d}x+\underset{2}{\overset{3}{\int }}\left(x-2\right)\text{d}x$

Câu 7. Hàm số $F\left(x\right)=\frac{x^3}{3}-\cos x$ là một nguyên hàm của hàm số nào sau đây?

A. $f\left(x\right)=3x^2+\cos x$.

B. $f\left(x\right)=x^2+\sin x$.

C. $f\left(x\right)=x^2-\sin x$.

D. $f\left(x\right)=\frac{x^4}{12}+\sin x$.

Hiển thị đáp án

Đáp án: B

Giải thích:

Hàm số F(x) là một nguyên hàm của hàm số f(x)

$\Rightarrow F^{\text{'}}\left(x\right)=f\left(x\right)$

Ta có $F^{\text{'}}\left(x\right)={\left(\frac{x^3}{3}-\cos x\right)}^{\text{'}}$

$=x^2+\sin x$

Câu 8. Tìm $\int {\left(2x+1\right)}^5\text{d}x$ ta được

A. $\frac{1}{12}{\left(2x+1\right)}^6+C$.

B. $\frac{1}{6}{\left(2x+1\right)}^5+C$.

C. ${\left(2x+1\right)}^4+C$.

D. $5{\left(2x+1\right)}^4+C$.

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có $\int {\left(2x+1\right)}^5\text{d}x=\frac{1}{2}\int {\left(2x+1\right)}^5\text{d}\left(2x+1\right)$

$=\frac{{\left(2x+1\right)}^6}{12}+C$

Câu 9. Nguyên hàm của hàm số $f\left(x\right)=x^2-3x+\frac{1}{x}$ với $x\ne 0$ là

A. $\frac{x^3}{3}-\frac{3x^2}{2}+\ln \left|x\right|+C$.

B. $\frac{x^3}{3}-\frac{3x^2}{2}+\frac{1}{x^2}+C$.

C. $x^3-3x^2+\ln x+C$.

D. $\frac{x^3}{3}-\frac{3x^2}{2}-\ln \left|x\right|+C$.

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có $\int f\left(x\right)\text{d}x=\int \left(x^2-3x+\frac{1}{x}\right)\text{d}x$

$=\frac{x^3}{3}-\frac{3x^2}{2}+\ln \left|x\right|+C$

Câu 10. Nguyên hàm $F\left(x\right)$ của hàm số $f\left(x\right)=\frac{2x^4+3}{x^2}$, $x\ne 0$ là

A. $F\left(x\right)=\frac{2x^3}{3}+\frac{3}{x}+C$.

B. $F\left(x\right)=-3x^3-\frac{3}{x}+C$.

C. $F\left(x\right)=\frac{x^3}{3}-\frac{3}{x}+C$.

D. $F\left(x\right)=\frac{2x^3}{3}-\frac{3}{x}+C$.

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có $\int \left(\frac{2x^4+3}{x^2}\right)\text{d}x=\int \left(2x^2+\frac{3}{x^2}\right)\text{d}x$

$=\frac{2x^3}{3}-\frac{3}{x}+C$

Xem thêm các bài tổng hợp lý thuyết Toán lớp 12 đầy đủ, chi tiết khác:

Lý thuyết Số phức

Lý thuyết Cộng, trừ và nhân số phức

Lý thuyết Phép chia số phức

Lý thuyết Phương trình bậc hai với hệ số thực

Lý thuyết Ôn tập chương 4