Lý thuyết Phương trình đường thẳng trong không gian (mới 2024 + Bài Tập) – Toán 12

Lý thuyết Toán 12 Bài 3: Phương trình đường thẳng trong không gian

Bài giảng Toán 12 Bài 3: Phương trình đường thẳng trong không gian

A. Lý thuyết

I. Phương trình tham số của đường thẳng

- Định lí:

Trong không gian Oxyz, cho đường thẳng ∆ đi qua điểm M₀ (x₀ ; y₀; z₀) và nhận vectơ $\overrightarrow{a}=\left(a_1;a_2;a_3\right)$ làm vectơ chỉ phương. Điều kiện cần và đủ để điểm M(x; y; z) nằm trên đường thẳng ∆ là có số thực t thỏa mãn: $\left\{\begin{array}{l}x=x_0+a_{1}t\\ y=y_0+a_{2}t\\ z=z_0+a_{2}t\end{array}\right.$

- Định nghĩa:

Phương trình tham số của đường thẳng ∆ đi qua điểm M₀ (x₀ ; y₀; z₀) và nhận vectơ $\overrightarrow{a}=\left(a_1;a_2;a_3\right)$ làm vectơ chỉ phương là $\left\{\begin{array}{l}x=x_0+a_{1}t\\ y=y_0+a_{2}t\\ z=z_0+a_{2}t\end{array}\right.$

Trong đó, t là tham số.

- Chú ý:

Nếu a₁ ; a₂; a₃ đều khác 0 thì ta có thể viết phương trình ∆ dưới dạng chính tắc như sau:

$\frac{x-x_0}{a_1}=\frac{y-y_0}{a_2}$$=\frac{z-z_0}{a_3}$

Ví dụ 1. Viết phương trình tham số của đường thẳng ∆ đi qua A(1; 2;2) và có vecto chỉ phương là $\overrightarrow{u}(1;2;-1)$

Lời giải:

Phương trình tham số của ∆ là: $\left\{\begin{array}{c}x=1+\text{}t\\ y=2+\text{}2t\\ z=2-t\end{array}\right.$

Ví dụ 2. Viết phương trình tham số của đường thẳng AB với A(0;1; 2); B(2; 2; 1).

Lời giải:

Đường thẳng AB nhận $\overrightarrow{AB}(2;1;-1)$ làm vecto chỉ phương.

Phương trình tham số của AB là: $\left\{\begin{array}{c}x=2\text{}t\\ y=1+\text{}t\\ z=2-t\end{array}\right.$.

II. Điều kiện để hai đường thẳng song song, cắt nhau và chéo nhau.

1. Điều kiện để hai đường thẳng song song.

Gọi $\overrightarrow{a}=(a_1;a_2;a_3);$$\overrightarrow{a\text{'}}=(a{\text{'}}_1;a{\text{'}}_2;a{\text{'}}_3)$ lần lượt là vecto chỉ phương của d và d’.

Lấy điểm M(x₀; y₀; z₀) trên d.

Ta có: d song song với d’ khi và chỉ khi $\left\{\begin{array}{c}\overrightarrow{a}=k.\overrightarrow{a\text{'}}\\ M\notin d\text{'}\end{array}\right.$

Đặc biệt: d trùng với d’ khi và chỉ khi: $\left\{\begin{array}{c}\overrightarrow{a}=k.\overrightarrow{a\text{'}}\\ M\in d\text{'}\end{array}\right.$

Ví dụ 3. Chứng minh hai đường thẳng sau đây song song với nhau:

$d:\left\{\begin{array}{c}x=3+\text{}2t\\ y=2-3t\\ z=2+t\end{array}\right.$;$\hspace{0.17em}\hspace{0.17em}d\text{'}:\left\{\begin{array}{c}x=1-\text{}4t\\ y=2+\text{}6t\\ z=-2t\end{array}\right.$

Lời giải:

Đường thẳng d có vecto chỉ phương $\overrightarrow{u}(2;-3;1)$ đi qua M(3; 2; 2).

Đường thẳng d’ có vecto chỉ phương là $\overrightarrow{v}(-4;6;-2)$

Ta thấy: $\overrightarrow{v}=-2\overrightarrow{u};M\notin d\text{'}$

Do đó, hai đường thẳng trên song song với nhau.

2. Điều kiện để hai đường thẳng cắt nhau.

- Hai đường thẳng d và d’ cắt nhau khi và chỉ khi hệ phương trình ẩn t và t’ sau:

$\left\{\begin{array}{c}{x}_0+\text{\hspace{0.17em}}t{a}_1=x{\text{'}}_0+\text{\hspace{0.17em}}t\text{'}.a{\text{'}}_1\\ y_0+\text{\hspace{0.17em}}t{a}_2=y{\text{'}}_0+\text{\hspace{0.17em}}t\text{'}.a{\text{'}}_2\\ z_0+\text{\hspace{0.17em}}t{a}_3=z{\text{'}}_0+\text{\hspace{0.17em}}t\text{'}.a{\text{'}}_3\end{array}\right.$ (I)

Có đúng một nghiệm.

- Chú ý: Giả sử hệ (I) có nghiệm (t₀ ; t’₀), để tìm giao điểm M₀ của d và d’ ta có thể thay t₀ vào phương trình tham số của d hoặc thay t’₀ vào phương trình tham số của d’.

Ví dụ 4. Tìm giao điểm của hai đường thẳng:

$d:\left\{\begin{array}{c}x=3+\text{}t\\ y=2-t\\ z=2+t\end{array}\right.$;$d\text{'}:\left\{\begin{array}{c}x=3-\text{}t\text{'}\\ y=2+t\text{'}\\ z=3\end{array}\right.$

Lời giải:

Xét hệ phương trình:

$$\begin{gathered} \left\{\begin{array}{c}3+t=3-t\text{'}\\ 2-t=2+\text{\hspace{0.17em}}t\text{'}\\ 2+\text{}t=3\end{array}\right. \\ \iff \left\{\begin{array}{c}t=-t\text{'}\\ t=-t\text{'}\\ t=1\end{array}\right. \\ \iff t=1;t\text{'}=-1 \end{gathered}$$

Suy ra, d cắt d’ tại điểm A(4; 1; 3).

3. Điều kiện để hai đường thẳng chéo nhau.

Hai đường thẳng d và d’ chéo nhau khi và chỉ khi $\overrightarrow{a};\overrightarrow{a\text{'}}$ không cùng phương và hệ phương trình $\left\{\begin{array}{c}{x}_0+\text{\hspace{0.17em}}t{a}_1=x{\text{'}}_0+\text{\hspace{0.17em}}t\text{'}.a{\text{'}}_1\\ y_0+\text{\hspace{0.17em}}t{a}_2=y{\text{'}}_0+\text{\hspace{0.17em}}t\text{'}.a{\text{'}}_2\\ z_0+\text{\hspace{0.17em}}t{a}_3=z{\text{'}}_0+\text{\hspace{0.17em}}t\text{'}.a{\text{'}}_3\end{array}\right.$ vô nghiệm.

Ví dụ 5. Xét vị trí tương đối của hai đường thẳng:

$d:\left\{\begin{array}{c}x=3+\text{}t\\ y=2-3t\\ z=2+t\end{array};\right.$$\hspace{0.17em}d\text{'}:\left\{\begin{array}{c}x=1-\text{}4t\text{'}\\ y=2+\text{}6t\text{'}\\ z=-2t\text{'}\end{array}\right.$

Lời giải:

Đường thẳng d có vecto chỉ phương $\overrightarrow{a}(1;-3;1)$

Đường thẳng d’ có vecto chỉ phương là $\overrightarrow{a\text{'}}(-4;6;-2)$

Ta thấy, không tồn tại số thực k để $\overrightarrow{a}=k\overrightarrow{a\text{'}}$ nên hai đường thẳng d và d’ cắt nhau hoặc chéo nhau.

Xét hệ phương trình:

$\left\{\begin{array}{c}3+\text{\hspace{0.17em}}t=1-4t\text{'}\left(1\right)\\ 2-3t=2+6t\text{'}\left(2\right)\\ 2+t=-2t\text{'}\left(3\right)\end{array}\right.$ (I)

Giải hệ phương trình (1) và (2) ta được: t =2; t’ = -1.

Thay vào (3) ta thấy không thỏa mãn nên hệ phương trình (I) vô nghiệm.

Vậy hai đường thẳng d và d’ chéo nhau.

- Nhận xét:

Trong không gian Oxyz, cho mặt phẳng (P): Ax + By + Cz + D = 0 và đường thẳng d: $\left\{\begin{array}{l}x=x_0+a_{1}t\\ y=y_0+a_{2}t\\ z=z_0+a_{2}t\end{array}\right.$

Xét phương trình A(x₀ + ta₁ ) + B(y₀ + ta₂ ) + C (z₀ + ta₃ ) + D = 0 ( t là ẩn ) (1)

- Nếu phương trình (1) vô nghiệm thì d và (P) không có điểm chung. Vậy d// (P).

- Nếu phương trình (1) có đúng một nghiệm t = t₀ thì d cắt (P) tại điểm M(x₀ + t₀ a₁;y₀ + t₀ a₂; z₀ + t₀ a₃).

- Nếu phương trình (1) có vô số nghiệm thì d thuộc (P).

Ví dụ 6. Xét vị trí tương đối của đường thẳng $d:\left\{\begin{array}{c}x=1+\text{}2t\\ \begin{array}{l}y=-t\\ z=-2+t\end{array}\end{array}\right.$và mặt phẳng (P): 2x – y – z = 0.

Lời giải:
Lấy điểm M(1+ 2t; -t; -2 + t) thuộc đường thẳng d.

Thay tọa độ điểm M vào phương trình (P) ta được:

2(1+ 2t) – (- t) – (-2+ t) = 0

$\iff$2 + 4t + t + 2 – t = 0

$\iff$4t + 4 = 0$\iff$t = - 1.

Suy ra đường thẳng d cắt mặt phẳng (P) tại M( -1; 1; - 3).

B. Bài tập tự luyện

Bài 1. Viết phương trình tham số của đường thẳng d trong mỗi trường hợp:

a) Đi qua hai điểm A( -2; 0; 1) và B(1; 1; 1).

b) Đi qua A( -2; 1; 1) và song song với đường thẳng $\left\{\begin{array}{c}x=1+\text{}2t\\ \begin{array}{l}y=-t\\ z=-2+t\end{array}\end{array}\right.$

c) Đi qua M(0; -2; 1) và vuông góc với mặt phẳng (P): x + 2y – z + 3 = 0.

Lời giải:

a) Đường thẳng AB đi qua điểm A(-2; 0; 1) và nhận vecto $\overrightarrow{AB}(3;1;0)$ làm vecto chỉ phương nên có phương trình: $\left\{\begin{array}{c}x=-2+\text{}3t\\ \begin{array}{l}y=t\\ z=1\text{\hspace{0.17em}}\end{array}\end{array}\right.$

b) Đường thẳng đã cho có vecto chỉ phương là $\overrightarrow{a}(2;-1;1)$

Vì đường thẳng d cần tìm song song với đường thẳng đã cho nên vecto chỉ phương của d là $\overrightarrow{a}(2;-1;1)$

Phương trình tham số của d là $\left\{\begin{array}{l}x=-2+\text{}2t\\ \begin{array}{l}y=1-\text{}t\\ z=1\text{\hspace{0.17em}\hspace{0.17em}}+\text{\hspace{0.17em}\hspace{0.17em}}t\end{array}\end{array}\right.$

c) Mặt phẳng (P) có vecto pháp tuyến là: $\overrightarrow{n}\text{}(1;2;-1)$

Vì d vuông góc với (P) nên vecto chỉ phương của d là $\overrightarrow{n}\text{}(1;2;-1)$

Phương trình tham số của d là $\left\{\begin{array}{c}x=\text{\hspace{0.17em}}t\\ \begin{array}{l}y=-2+2\text{}t\\ z=1\text{\hspace{0.17em}\hspace{0.17em}}-t\end{array}\end{array}\right.$

Bài 2. Xét vị trí tương đối của hai đường thẳng sau:

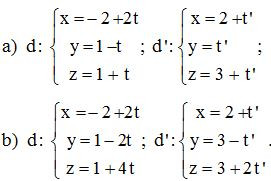
Lời giải:

a) Đường thẳng d và d’ có vecto chỉ phương lần lượt là: $\overrightarrow{a}(2;-1;1);$$\hspace{0.17em}\overrightarrow{a\text{'}}(1;1;1)$

Không tồn tại số thực k để $\overrightarrow{a}=k.\overrightarrow{a\text{'}}$ nên hai đường thẳng trên sẽ cắt nhau hoặc chéo nhau.

Xét hệ phương trình: $\left\{\begin{array}{c}-2+\text{}2t=2+\text{}t\text{'}\left(1\right)\\ \begin{array}{l}1-\text{}t=t\text{'}\left(2\right)\\ 1\text{\hspace{0.17em}\hspace{0.17em}}+\text{\hspace{0.17em}\hspace{0.17em}}t=3+t\text{'}\left(3\right)\end{array}\end{array}\right.$ (I)

Giải hệ phương trình (1) và (2) ta được: $t=\frac{5}{3};t\text{'}=\frac{-2}{3}$

Thay vào (3) ta thấy không thỏa mãn nên hệ phương trình (I) vô nghiệm nên hai đường thẳng đã cho chéo nhau.

b). Đường thẳng d và d’ có vecto chỉ phương lần lượt là: $\overrightarrow{a}(2;-2;4);$$\overrightarrow{a\text{'}}(1;-1;2)$

Đường thẳng d đi qua điểm M(-2; 1;1)

Ta thấy: $\overrightarrow{a}=2.\overrightarrow{a\text{'}}$ và điểm M không thuộc đường thẳng d’ nên hai đường thẳng trên song song với nhau.

Bài 3. Tìm số điểm chung của đường thẳng d và mặt phẳng (P) biết:

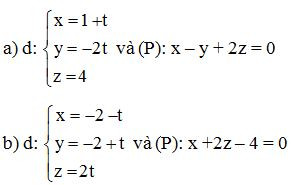
Lời giải:

Trắc nghiệm Toán 12 Bài 3: Phương trình đường thẳng trong không gian

Câu 1: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng $d:\frac{x-1}{4}=\frac{y}{-1}=\frac{z+1}{3}$ và điểm $M\left(1;3;-3\right)$. Phương trình mặt phẳng đi qua M và vuông góc với d là

A. $x-z-4=0.$

B. $2x-y+3z+10=0.$

C. $2x-y+3z+5=0.$

D. $x+3y-3z+10=0.$

Hiển thị đáp án

Đáp án: B

Giải thích:

$\overrightarrow{n_P}=\overrightarrow{u_d}=(2;-1;3)$

$\to \left(P\right):2x-y+3z+10=0$

Câu 2: Trong không gian với hệ tọa độ Oxyz, cho hai điểm $A\left(0;-2;1\right)$ và $B\left(4;-8;-1\right)$. Phương trình chính tắc của đường thẳng đi qua hai điểm A và B là

A. $\frac{x}{2}=\frac{y+2}{-3}=\frac{z-1}{-1}.$

B. $\frac{x-4}{4}=\frac{y+8}{-6}=\frac{z-1}{-2}.$

C. $\frac{x}{2}=\frac{y-2}{-3}=\frac{z+1}{1}.$

D. $\frac{x+1}{4}=\frac{y-2}{-6}=\frac{z-1}{2}.$

Hiển thị đáp án

Đáp án: A

Giải thích:

$\overrightarrow{AB}=(4;-6;-2)$

$\Rightarrow AB:\frac{x}{2}=\frac{y+2}{-3}=\frac{z-1}{-1}$

Câu 3: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng $\Delta :\left\{\begin{array}{l}x=1+t\\ y=2-2t\\ z=3+t\end{array}\right.$. Điểm M nào thuộc $\Delta$?

A. M(2;1;3)

B. M(2;0;4)

C. M(1;-2;3)

D. M(1;2;-3)

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta thấy tọa độ điểm M(2; 0; 4) thỏa mãn $∆$ nên M(2; 0; 4) $\in ∆$

Câu 4: Trong không gian với hệ tọa độ Oxyz, cho điểm $A\left(1;3;1\right),B\left(3;2;-2\right)$. Gọi d là đường thẳng đi qua A, B. Phương trình nào sau đây không phải là phương trình của đường thẳng d ?

A. $\left\{\begin{array}{l}x=1+2t\\ y=3-t\\ z=1-3t\end{array}\right.$

B. $\left\{\begin{array}{l}x=3+2t\\ y=3-t\\ z=1-3t\end{array}\right.$

C. $\left\{\begin{array}{l}x=5+2t\\ y=1-t\\ z=-5-3t\end{array}\right.$

D. $\left\{\begin{array}{l}x=3-2t\\ y=2+t\\ z=-2+3t\end{array}\right.$

Hiển thị đáp án

Đáp án: B

Giải thích:

Câu 5: Trong không gian với hệ tọa độ Oxyz, cho hai điểm $A\left(1;1;0\right)$ và $B\left(0;1;2\right)$. Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng AB?

A. $\overrightarrow{b}=\left(-1;0;2\right).$

B. $\overrightarrow{c}=\left(1;2;2\right).$

C. $\overrightarrow{d}=\left(-1;2;2\right).$

D. $\overrightarrow{a}=\left(-1;0;-2\right).$

Hiển thị đáp án

Đáp án: A

Giải thích:

$\overrightarrow{AB }=(-1; 0; 2)$

Câu 6: Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;2;3). Gọi $M_1,M_2$ lần lượt là hình chiếu vuông góc của M trên các trục Ox, Oy. Vectơ nào dưới đây là vectơ chỉ phương của đường thẳng $M_1{M}_2$?

A. $\overrightarrow{u_2}=\left(1;2;0\right).$

B. $\overrightarrow{u_3}=\left(1;0;0\right).$

C. $\overrightarrow{u_4}=\left(-1;2;0\right).$

D. $\overrightarrow{u_4}=\left(-1;2;0\right).$

Hiển thị đáp án

Đáp án: C

Giải thích:

$M_1(1;0;0),M_2(0;2;0)$

$\Rightarrow \overrightarrow{M_1{M}_2}=(-1;2;0)$

Câu 7: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng $d:\left\{\begin{array}{l}x=1-t\\ y=2+3t\\ z=2+t\end{array}\right.\left(t\in ℝ\right)$. Vectơ nào dưới đây là vectơ chỉ phương của đường thẳng d ?

A. $\overrightarrow{u}=\left(-1;3;-1\right).$

B. $\overrightarrow{u}=\left(1;2;2\right).$

C. $\overrightarrow{u}=\left(-1;3;2\right).$

D. $\overrightarrow{u}=\left(-1;3;1\right).$

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có: $\overrightarrow{u}=(-1; 3; 1)$

Câu 8: Trong không gian với hệ tọa độ Oxyz, cho hai điểm $A\left(2;-1;3\right),B\left(3;2;-1\right)$. Phương trình nào sau đây là phương trình đường thẳng AB ?

A. $\left\{\begin{array}{l}x=1+2t\\ y=3-t\\ z=-4+3t\end{array}\right.$

B. $\left\{\begin{array}{l}x=2+t\\ y=-1+3t\\ z=3-4t\end{array}\right.$

C. $\left\{\begin{array}{l}x=2+t\\ y=-1+t\\ z=3-4t\end{array}\right.$

D. $\left\{\begin{array}{l}x=1+2t\\ y=1-t\\ z=-4+3t\end{array}\right.$

Hiển thị đáp án

Đáp án: B

Giải thích:

$\overrightarrow{AB}=(1;3;-4)$

$\Rightarrow d:\{\begin{array}{l}x=2+t\\ y=-1+3t\\ z=3-4t\end{array}$

Câu 9: Trong không gian với hệ tọa độ Oxyz, cho $d:\left\{\begin{array}{l}x=1+t\\ y=2-2t\\ z=3+t\end{array}\right.$. Điểm nào sau đây không thuộc đường thẳng d ?

A. $M\left(0;4;2\right).$

B. $N\left(1;2;3\right).$

C. $P\left(1;-2;3\right).$

D. $Q\left(2;0;4\right).$

Hiển thị đáp án

Đáp án: C

Giải thích: Ta thấy: $P\left(1; -2; 3\right)\notin d$

Câu 10: Trong không gian với hệ tọa độ Oxyz, phương trình tham số của đường thẳng d đi qua hai điểm $A\left(1;2;-3\right)$ và $B\left(3;-1;1\right)$ là

A. $\left\{\begin{array}{l}x=1+t\\ y=-2+2t\\ z=-1-3t\end{array}\right.$

B. $\left\{\begin{array}{l}x=1+3t\\ y=-2-t\\ z=-3-t\end{array}\right.$

C. $\left\{\begin{array}{l}x=-1+2t\\ y=-2-3t\\ z=3+4t\end{array}\right.$

D. $\left\{\begin{array}{l}x=-1+2t\\ y=5-3t\\ z=-7+4t\end{array}\right.$

Hiển thị đáp án

Đáp án: D

Giải thích:

$\overrightarrow{AB}=(2;-3;4)$

$\Rightarrow d:\{\begin{array}{l}x=-1+2t\\ y=5-3t\\ z=-7+4t\end{array}$

Xem thêm các bài tổng hợp lý thuyết Toán lớp 12 đầy đủ, chi tiết khác:

Lý thuyết Mặt cầu

Lý thuyết Ôn tập chương 2

Lý thuyết Hệ tọa độ trong không gian

Lý thuyết Phương trình mặt phẳng

Lý thuyết Ôn tập chương 3