Nội dung bài viết

    Xem thêm

    Lý thuyết Phương trình bậc hai với hệ số thực (mới 2024 + Bài Tập) – Toán 12

    Lý thuyết Phương trình bậc hai với hệ số thực lớp 12 gồm lý thuyết chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm Toán 12 Bài 4: Phương trình bậc hai với hệ số thực.

    1 2,663 21/12/2023
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Lý thuyết Toán 12 Bài 4: Phương trình bậc hai với hệ số thực

    Bài giảng Toán 12 Bài 4: Phương trình bậc hai với hệ số thực

    A. Lý thuyết

    1. Căn bậc hai của số thực âm

    Tương tự căn bậc hai của một số thực dương, từ i2 = –1, ta nói i là một căn bậc hai của – 1; – i cũng là một căn bậc hai của –1 vì (–i)2 = –1.

    Từ đó, ta xác định được căn bậc hai của các số thực âm, chẳng hạn.

    Căn bậc hai của –16 là ±4i vì ±4i2=−16

    Căn bậc hai của –5 là ±  5i vì ±  5i2=−5

    Tổng quát, các căn bậc hai của số thực a âm là ±ia.

    2. Phương trình bậc hai với hệ số thực

    Cho phương trình bậc hai ax2 + bx + c = 0 với a; b ; c∈ℝ; a  ≠  0.

    Xét biệt số ∆ = b2 – 4ac của phương trình. Ta thấy:

    Khi ∆ = 0, phương trình có một nghiệm thực x  =  −b2a.

    Khi ∆ > 0, có hai căn bậc hai thực của ∆ là ±Δ và phương trình có hai nghiệm thực phân biệt, được xác định bởi công thức x1;2  =  −b±Δ2a.

    Khi ∆ < 0, ta có hai căn bậc hai thuần ảo của ∆ là ±i Δ. Khi đó, phương trình có hai nghiệm phức được xác định bởi công thức x1;2  =  −b±iΔ2a.

    – Nhận xét:

    Trên tập hợp số phức, mọi phương trình bậc hai đều có hai nghiệm (không nhất thiết phân biệt).

    Tổng quát: Mọi phương trình bậc n (n≥1):

    a0.xn + a1.xn – 1 + ….+ an–1.x + an = 0

    Trong đó; a0 ; a1;…..; an∈ℂ;  a0  ≠0đều có n nghiệm phức (các nghiệm không nhất thiết phân biệt).

    B. Bài tập tự luyện

    Bài 1. Tìm các căn bậc hai phức của các số sau: – 10; – 15; – 73; –144.

    Lời giải:

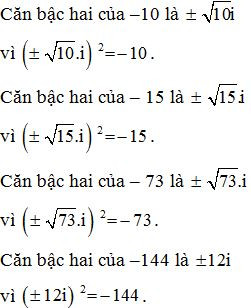
    Lý thuyết Phương trình bậc hai với hệ số thực chi tiết – Toán lớp 12 (ảnh 1)

    Bài 2. Giải các phương trình sau trên tập hợp số phức:

    a) 2z2 + 4z + 3 = 0;

    b) 5z2 – 3z + 1 = 0;

    c) –z2 – 4z – 8 = 0.

    Lời giải:

    a) 2z2 + 4z + 3 = 0 có a = 2; b = 4; c = 3

    ∆ = 42 – 4. 2.3 = – 8 < 0

    Suy ra, phương trình đã cho có 2 nghiệm phức phân biệt là:

    z1;2  =  −4±i82.2 = −1  ±22.i

    b) 5z2 – 3z + 1 = 0 có a = 5; b = –3; c = 1

    ∆ = (–3)2 – 4. 5.1 = –11 < 0

    Suy ra, phương trình đã cho có 2 nghiệm phức phân biệt là:

    z1;2  =  3±i112.5=310±1110i

    c) – z2 – 4z – 8 = 0 có a = –1; b = – 4; c = –8

    ∆ = (– 4)2 – 4.(–1).(–8) = 16 – 32 = –16 < 0

    Suy ra, phương trình đã cho có 2 nghiệm phức phân biệt là:

    z1;2  =  4±4i2.(−1) =−2±2i

    Bài 3. Giải các phương trình sau trên tập hợp số phức:

    a) z4 + 3z2 + 2 = 0;

    b) z4 – 3z2 – 18 = 0.

    Lời giải:

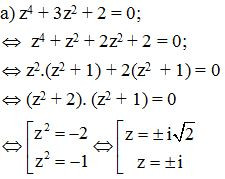
    Lý thuyết Phương trình bậc hai với hệ số thực chi tiết – Toán lớp 12 (ảnh 1)

    Vậy tập nghiệm của phương trình đã cho là S​  =  i;  −i; i2;  −i2.

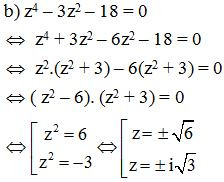
    Lý thuyết Phương trình bậc hai với hệ số thực chi tiết – Toán lớp 12 (ảnh 1)

    Vậy tập nghiệm của phương trình đã cho là là S =  ±i3;  ±6

    Trắc nghiệm Toán 12 Bài 4: Phương trình bậc hai với hệ số thực

    Câu 1: (Đề tham khảo – Bộ GD & ĐT 2018) Gọi z1 và z2 là hai nghiệm phức của phương trình 4z2−4z+3=0. Giá trị của biểu thức z1+z2 bằng

    A. 32

    B. 23

    C. 3

    D. 3

    Đáp án: D

    Giải thích:

    Ta có 4z2−4z+3=0

    ⇔z=12±22i

    ⇒|z1|+|z2|=3

    Câu 2: (Đề thi THPT Quốc gia năm 2017 – Mã đề 101) Phương trình nào dưới đây nhận hai số phức 1+2i và 1-2i là nghiệm?

    A. z2+2z+3=0

    B. z2−2z−3=0

    C. z2−2z+3=0

    D. z2+2z−3=0

    Đáp án: C

    Giải thích:

    Ta có 1+2i+1−2i=21+2i1−2i=3

    ⇒z2−2z+3=0.

    Câu 3: (Đề thi THPT Quốc gia năm 2017 – Mã đề 102) Kí hiệu z1,z2 là hai nghiệm phức của phương trình 3z2−z+1=0 . Tính P=z1+z2 .

    A. P=33

    B. P=233

    C. P=23

    D. P=143

    Đáp án: B

    Giải thích:

    3z2−z+1=0

    ⇔z=16±116i

    ⇒P=|z1|+|z2|=233.

    Câu 4: (Đề thi THPT Quốc gia năm 2017 – Mã đề 103) Kí hiệu z1,z2 là hai nghiệm phức của phương trình z2−z+6=0 . Tính P=1z1+1z2 .

    A. P=16

    B. P=112

    C. P=−16

    D. P=6

    Đáp án: A

    Giải thích:

    Ta có z1+z2=1z1z2=6

    ⇒P=1z1+1z2

    =z2+z2z1z2=16.

    Câu 5: (Đề thi THPT Quốc gia năm 2017 – Mã đề 103) Kí hiệu z1,z2 là hai nghiệm của phương trình z2+4=0 . Gọi M,N lần lượt là điểm biểu diễn của z1,z2 trên mặt phẳng tọa độ. Tính T=OM+ON với O là gốc tọa độ.

    A. 2

    B. 2

    C. 8

    D. 4

    Đáp án: D

    Giải thích:

    Ta có: z2+4=0

    ⇔z=±2i

    ⇒M(0;2),N(0;−2)

    ⇒T=OM+ON=4.

    Câu 6: (Đề minh họa lần 1 – Bộ GD & ĐT năm 2017) Kí hiệu z1,z2,z3 và z4 là bốn nghiệm phức của phương trình z4−z2−12=0 . Tính T=z1+z2+z3+z4.

    A. T=4

    B. T=23

    C. T=4+23

    D. T=2+23

    Đáp án: C

    Giải thích:

    Ta có:

    z4−z2−12=0

    ⇔[z2=4z2=−3⇔[z=±2z=±3i

    ⇒T=|z1|+|z2|+|z3|+|z4|

    =4+23.

    Câu 7: (Đề minh họa lần 2 – Bộ GD & ĐT năm 2017) Kí hiệu z0 là nghiệm phức có phần ảo dương của phương trình 4z2−16z+17=0 . Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức w=iz0 ?

    A. M112;2

    B. M2−12;2

    C. M3−14;1

    D. M414;1

    Đáp án: B

    Giải thích:

    Ta có: 4z2−16z+17=0

    ⇔z=2±12i

    ⇒z0=2+12i

    ⇒w=iz0=−12+2i

    ⇒M(−12;2).

    Câu 8: (Đề minh họa lần 3 – Bộ GD & ĐT năm 2017) Kí hiệu z1,z2 là hai nghiệm của phương trình z2+z+1=0 . Tính P=z12+z22+z1z2 .

    A. 1

    B. 2

    C. -1

    D. 0

    Đáp án: D

    Giải thích:

    Ta có: z1+z2=−1z1z2=1

    ⇒P=z12+z22+z1z2

    =(z1+z2)2−z1z2=0.

    Câu 9: (Sở GD & ĐT Tp. Hồ Chí Minh cụm 2 năm 2017) Gọi z1,z2 nghiệm của phương trình z2+4z+5=0 .Tìm w=1+z1100+1+z2100 .

    A. w=250i

    B. w=−251

    C. w=251

    D. w=−250i

    Đáp án: B

    Giải thích:

    Ta có: z2+4z+5=0⇔z=−2±i

    Do đó w=1+z1100+1+z2100

    =(1+i)100+(1−i)100

    =(2i)50+(−2i)50

    =−2.250=−251.

    Câu 10: (Sở GD & ĐT Tp. Hồ Chí Minh cụm 6 năm 2017) Tìm các căn bậc hai của -12 trong tập số phức ℂ .

    A. ±43i

    B. ±23i

    C. ±22i

    D. ±32i

    Đáp án: B

    Giải thích:

    Ta có: -12=12i2=±23i

    Xem thêm các bài tổng hợp lý thuyết Toán lớp 12 đầy đủ, chi tiết khác:

    Lý thuyết Ôn tập chương 4

    Lý thuyết Khái niệm về khối đa diện

    Lý thuyết Khối đa diện lồi và khối đa diện đều

    Lý thuyết Khái niệm về thể tích của khối đa diện

    Lý thuyết Ôn tập chương 1

    Tham khảo các loạt bài Toán 12 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 2,663 21/12/2023
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: