Lý thuyết Lôgarit (2024) và bài tập có đáp án

Lý thuyết Lôgarit lớp 12 gồm lý thuyết chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm Toán 12 Bài 3: Lôgarit.

1 3,316 26/09/2024

Tải về

Trang trước

Trang sau

Lý thuyết Toán 12 Bài 3: Lôgarit

Bài giảng Toán 12 Bài 3: Lôgarit

I. Lý thuyết về lôgarit

1. Định nghĩa logarit

Cho hai số dương a; b với a ≠ 1. Số α thỏa mãn đẳng thức a^α = b được gọi là logarit cơ số a của b và kí hiệu là log_ab.

$α = \log_{a} b \Leftrightarrow a^{α} = b$

Ví dụ 1.

a) log₃ 27 = 3 vì 3³ = 27.

b) $\log_{4} (\frac{1}{16}) = - 2$ vì $4^{- 2} = \frac{1}{16}$ .

– Chú ý: Không có logarit của số âm và số 0.

2. Tính chất của logarit

Cho hai số dương a và b; a ≠ 1. Ta có các tính chất sau đây:

log_a1 = 0; log_aa = 1

$a^{\log_{a} b} = b; \log_{a} (a^{α}) = α$

Ví dụ 2.

$4^{- 2 \log_{4} 3} = {(4^{\log_{4} 3})}^{- 2}$ $= 3^{- 2} = \frac{1}{9}$

$\log_{3} (\frac{1}{27})$ $= \log_{3} (3^{- 3}) = - 3$

II. Quy tắc tính logarit

1. Logarit của một tích

– Định lí 1. Cho ba số dương a; b₁ ;b₂ với a ≠ 1. Ta có:

$\log_{a} (b_{1} . b {}_{2}) = \log_{a} b_{1} + \log_{a} b {}_{2}$

Logarit của một tích bằng tổng các logarit.

Ví dụ 3.

$\log_{2} 12 + \log_{2} \frac{1}{3} = \log_{2} (12. \frac{1}{3}) = \log_{2} 4 = 2$

– Chú ý:

Định lí 1 có thể mở rộng cho tích n số dương:

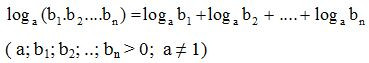
Lý thuyết Lôgarit chi tiết – Toán lớp 12 (ảnh 1)

2. Logarit của một thương

– Định lí 2. Cho ba số dương a; b₁ ;b₂ với a ≠ 1. Ta có:

$\log_{a} \frac{b_{1}}{b_{2}} = \log_{a} b_{1} - \log_{a} b {}_{2}$

Logarit của một thương bằng hiệu các logarit.

Đặc biệt: $\log_{a} \frac{1}{b} = - \log_{a} b$ ( a > 0; b > 0; a ≠ 1)

– Ví dụ 4.

$\log {}_{5} 75 - \log_{5} 3 = \log_{5} \frac{75}{3} = \log_{5} 25 = 2$

3. Logarit của một lũy thừa

– Định lí 3. Cho hai số dương a; b và a ≠ 1 . Với mọi số α, ta có:

$\log_{a} b^{α} = α \log_{a} b$

Logarit của một lũy thừa bằng tích của số mũ với logarit của cơ số.

– Đặc biệt: $\log_{a} \sqrt[n]{b} = \frac{1}{n} \log_{a} b$

– Ví dụ 5.

$\begin{array}{l} \log_{7} 3^{6} = 6 \log_{7} 3 \\ \log_{3} \sqrt[5]{4} = \frac{1}{5} \log_{3} 4 \end{array}$

III. Đổi cơ số logarit

– Định lí 4. Cho ba số dương a; b; c với a ≠ 1; c ≠ 1, ta có:

$\log_{a} b = \frac{\log_{c} b}{\log_{c} a}$

– Đặc biệt:

$\begin{array}{l} \log_{a} b = \frac{1}{\log_{b} a} ( b \neq 1) \\ \log_{a^{α}} b = \frac{1}{α} \log_{a} b (α \neq 0) \end{array}$

Ví dụ 6. Tính giá trị các biểu thức sau:

a) $5^{\log_{\frac{1}{125}} 8}$

b) $\log_{2} 3. \log_{3} 4. .... \log_{7} 8$

Lời giải:

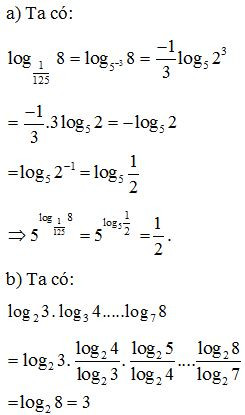
Lý thuyết Lôgarit chi tiết – Toán lớp 12 (ảnh 1)

IV. Logarit thập phân. Logarit tự nhiên

1. Logarit thập phân

Logarit thập phân là logarit cơ số 10.

log₁₀b thường được viết là logb hoặc lgb.

2. Logarit tự nhiên

– Logarit tự nhiên là logarit cơ số e.

log_eb được viết là lnb.

V. Bài tập vận dụng

Bài 1. Tính:

a) $a^{\log_{\sqrt[]{a}} 8}$ với a > 0.

b) $4^{3 \log_{8} 3 + 2 \log_{16} 5}$

c) $a^{4 l o g_{a^{2}} 10}$

Lời giải:

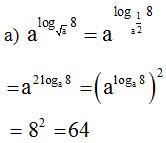
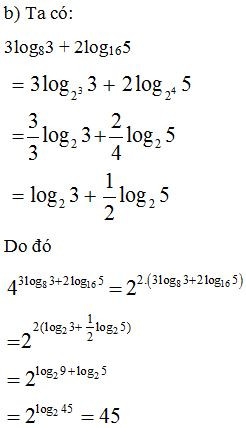
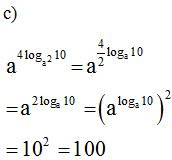
Lý thuyết Lôgarit chi tiết – Toán lớp 12 (ảnh 1)

Bài 2. Tính

a) $\frac{1}{2} \log_{7} 36 - \log_{7} 14 - 3 \log_{7} \sqrt[3]{21}$ ;

b) $3 \log_{3} 2 + \log_{9} 25 - \log_{\sqrt{3}} 3$ ;

c) $\log_{\sqrt{a}} b^{3} . \log_{b} a^{4}$ (a > 0; b > 0 và a; b đều khác 1).

Lời giải:

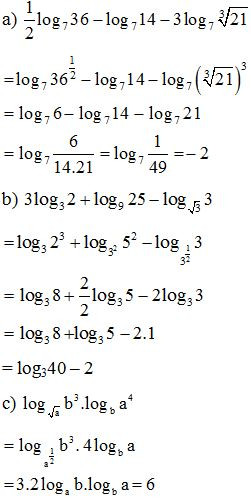
Lý thuyết Lôgarit chi tiết – Toán lớp 12 (ảnh 1)

Bài 3. Biết log₇2 = m. Tính giá trị của biểu thức log₄₉ 28 theo m?

Lời giải:

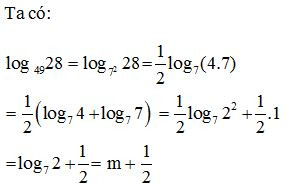
Lý thuyết Lôgarit chi tiết – Toán lớp 12 (ảnh 1)

Trắc nghiệm Logarit

Câu 1. Cho các mệnh đề sau:

(I). Cơ số của logarit phải là số nguyên dương.

(II). Chỉ số thực dương mới có logarit.

(III). $\ln (A + B) = \ln A + \ln B$ với mọi $A > 0, B > 0$ .

(IV) $\log_{a} b . \log_{b} c . \log_{c} a = 1$ , với mọi $a, b, c \in ℝ$ .

Số mệnh đề đúng là:

A. 1.

B. 2.

C. 3.

D. 4.

Hiển thị đáp án

Đáp án: A

Giải thích:

Cơ số của lôgarit phải là số dương khác 1. Do đó (I) sai.

Rõ ràng (II) đúng theo lý thuyết SGK.

Ta có $\ln A + \ln B = \ln (A . B)$ với mọi $A > 0, B > 0$ . Do đó (III) sai.

Ta có $\log_{a} b . \log_{b} c . \log_{c} a = 1$ với mọi $0 < a, b, c \neq 1$ . Do đó (IV) sai.

Vậy chỉ có mệnh đề (II) đúng.

Câu 2. Cho $a, A, B, M, N$ là các số thực với $a, M, N$ dương và khác 1. Có bao nhiêu phát biểu đúng trong các phát biểu dưới đây?

(I). Nếu $C = \sqrt{A B}$ với $A B > 0$ thì $2 \ln C = \ln A + \ln B$

(II). $(a - 1) \log_{a} x \geq 0 \Leftrightarrow x \geq 1$

(III). $M^{\log_{a} N} = N^{\log_{a} M}$

(IV). $\lim_{x \to + \infty} (\log_{\frac{1}{2}} x) = - \infty$

A. 1.

B. 2.

C. 3.

D. 4.

Hiển thị đáp án

Đáp án: C

Giải thích:

Nếu $C = \sqrt{A B}$ với $A B > 0$ thì $2 \ln C = \ln |A| + \ln |B|$ . Do đó (I) sai.

● Với $a > 1$ thì $(a - 1) \log_{a} x \geq 0$

$\Leftrightarrow \log_{a} x \geq 0 \Leftrightarrow x \geq 1$

● Với $0 < a < 1$ thì $(a - 1) \log_{a} x \geq 0$

$\Leftrightarrow \log_{a} x \leq 0 \Leftrightarrow x \geq 1$

Do đó (II) đúng.

Lấy lôgarit cơ số a hai vế của $M^{\log_{a} N} = N^{\log_{a} M}$ , ta có

$\log_{a} (M^{\log_{a} N}) = \log_{a} (N^{\log_{a} M})$

$\Leftrightarrow \log_{a} N . \log_{a} M = \log_{a} M . \log_{a} N$ .

Do đó (III) đúng.

Ta có $\lim_{x \to + \infty} (\log_{\frac{1}{2}} x) = \lim_{x \to + \infty} [- \log_{2} x]$

$= - \lim_{x \to + \infty} (\log_{2} x) = - \infty$

Do đó (IV) đúng.

Vậy ta có các mệnh đề (II), (III) và (IV) đúng.

Câu 3. Điều kiện để $\log_{a} b$ có nghĩa là:

A. $a < 0, b > 0$

B. $0 < a \neq 1, b < 0$

C. $0 < a \neq 1, b > 0$

D. $0 < a \neq 1, 0 < b \neq 1$

Hiển thị đáp án

Đáp án: C

Giải thích:

Điều kiện để $\log_{a} b$ có nghĩa là: $0 < a \neq 1, b > 0$

Câu 4. Điều kiện để biểu thức $\log_{2} (3 - x)$ xác định là:

A. $x \leq 3$

B. $x > 3$

C. $x \geq 3$

D. $x < 3$

Hiển thị đáp án

Đáp án: D

Giải thích:

Để biểu thức $\log_{2} (3 - x)$ xác định thì 3-x>0 => x < 3

Câu 5. Cho hàm số $f (x) = {(x^{1 + \frac{1}{2 \log_{4} x}} + 8^{\frac{1}{3 \log_{x^{2}} 2}} + 1)}^{\frac{1}{2}} - 1$ với $0 < x \neq 1$ . Tính giá trị biểu thức $P = f (f (2017)) .$

A. $P = 2016.$

B. $P = 1009.$

C. $P = 2017.$

D. $P = 1008.$

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có

$\begin{array}{l} x^{1 + \frac{1}{2 \log_{4} x}} = x^{1 + \frac{1}{\log_{2} x}} \end{array}$

$= x^{1 + \log_{x} 2} = x^{\log_{x} (2 x)} = 2 x$

$8^{\frac{1}{3 \log_{x^{2}} 2}} = 2^{3. \frac{1}{3. \log_{x^{2}} 2}}$

$= 2^{\frac{1}{\log_{x^{2}} 2}} = 2^{\log_{2} x^{2}} = x^{2}$

Khi đó $f (x) = {(x^{2} + 2 x + 1)}^{\frac{1}{2}} - 1$

$= {[{(x + 1)}^{2}]}^{\frac{1}{2}} - 1 = x .$

Suy ra $f (2017) = 2017$

$\overset{}{\to} f (f (2017)) = f (2017) = 2017.$

Câu 6. Với điều kiện các logarit đều có nghĩa, chọn mệnh đề đúng?

A. $\log_{a} (b c) = \log_{a} b + \log_{b} c$

B. $\log_{a} \frac{b}{c} = \log_{a} b + \log_{a} c$

C. $\log_{a} \frac{b}{c} = \frac{\log_{a} b}{\log_{a} c}$

D. $\log_{a} (b c) = \log_{a} b + \log_{a} c$

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có: $\log_{a} (b c) = \log_{a} b + \log_{a} c$ $(0 < a \neq 1; b, c > 0)$

$\log_{a} (\frac{b}{c}) = \log_{a} b - \log_{a} c$ $(0 < a \neq 1; b, c > 0)$

Câu 7. Nếu a > 1 và b > c > 0 thì:

A. $\log_{a} b > \log_{a} c$

B. $\log_{a} b < \log_{a} c$

C. $\log_{a} b < \log_{b} c$

D. $\log_{a} b > \log_{c} b$

Hiển thị đáp án

Đáp án: A

Giải thích:

Nếu a > 1 và b > c > 0 thì log_ab > log_ac

Câu 8. Cho $a, b$ là các số thực dương khác 1 và thỏa mãn $a b \neq 1.$ Rút gọn biểu thức $P = (\log_{a} b + \log_{b} a + 2) (\log_{a} b - \log_{a b} b) \log_{b} a - 1$ .

A. $P = \log_{b} a .$

B. $P = 1.$

C. $P = 0 .$

D. $P = \log_{a} b .$

Hiển thị đáp án

Đáp án: D

Giải thích:

Từ giả thiết, ta có

$P = (\log_{a} b + \log_{b} a + 2)$

$\times (\log_{a} b - \frac{1}{1 + \log_{b} a}) . \log_{b} a - 1$

$\overset{t = \log_{b} a}{\to} (t + \frac{1}{t} + 2) (\frac{1}{t} - \frac{1}{t + 1}) t - 1$

$= \frac{{(t + 1)}^{2}}{t} . \frac{1}{t (t + 1)} t - 1$

$= \frac{t + 1}{t} - 1 = \frac{1}{t} = \log_{a} b .$

Câu 9. Cho ba điểm $A (b; \log_{a} b), B (c; 2 \log_{a} c)$ , $C (b; 3 \log_{a} b)$ với $0 < a \neq 1,$ $b > 0$ . Biết B là trọng tâm của tam giác OAC với O là gốc tọa độ. Tính $S = 2 b + c .$

A. 9

B. 7

C. 11

D. 5

Hiển thị đáp án

Đáp án: A

Giải thích:

Vì B là trọng tâm của tam giác OAC nên

$\{\begin{cases} \frac{0 + b + b}{3} = c \\ \frac{0 + \log_{a} b + 3 \log_{a} b}{3} = 2 \log_{a} c \end{cases}$

$\Leftrightarrow \{\begin{cases} b + b = 3 c \\ 4 \log_{a} b = 6 \log_{a} c \end{cases}$

$\Leftrightarrow {\begin{cases} 2 b = 3 c \\ 2 \log_{a} b = 3 \log_{a} c \end{cases}$

$\Leftrightarrow {\begin{cases} 2 b = 3 c \\ \log_{a} b^{2} = \log_{a} c^{3} \end{cases}$

$\Leftrightarrow \{\begin{cases} 2 b = 3 c \\ b^{2} = c^{3} \end{cases}$

$\overset{c > 0}{\to} {\begin{cases} b = \frac{27}{8} \\ c = \frac{9}{4} \end{cases}$

$\overset{}{\to} S = 2 b + c = 9.$

Câu 10. Cho a là số thực dương khác 4. Tính $I = \log_{\frac{a}{4}} (\frac{a^{3}}{64})$

A. $I = 3$

B. $I = \frac{1}{3}$

C. $I = - \frac{1}{3}$

D. $I = - 3$

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có: $I = \log_{\frac{a}{4}} (\frac{a^{3}}{64})$

$= \log_{\frac{a}{4}} {(\frac{a}{4})}^{3}$

$= 3 \log_{\frac{a}{4}} \frac{a}{4} = 3$

Xem thêm các bài tổng hợp lý thuyết Toán lớp 12 đầy đủ, chi tiết khác:

Lý thuyết Hàm số mũ. Hàm số logarit

Lý thuyết Phương trình mũ và phương trình logarit

Lý thuyết Bất phương trình mũ và bất phương trình logarit

Lý thuyết Ôn tập chương 2

Lý thuyết Nguyên hàm

1 3,316 26/09/2024

Tải về

Trang trước

Trang sau

Xem thêm các chương trình khác:

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3