Lý thuyết Số phức (mới 2024 + Bài Tập) – Toán 12

Lý thuyết Toán 12 Bài 1: Số phức

Bài giảng Toán 12 Bài 1: Số phức

A. Lý thuyết

1. Số i.

Số i là số thỏa mãn: i² = –1.

2. Định nghĩa số phức

Mỗi biểu thức dạng a + bi , trong đó $a;b\in R$; i² = –1 được gọi là một số phức.

Đối với số phức z = a + bi, ta nói: a là phần thực, b là phần ảo của z.

Tập hợp các số phức kí hiệu là C.

Ví dụ 1. Các số sau là những số phức: 2 – 3i; –8 + 4i; $5-i\sqrt{2};$$\sqrt{3}+\text{}2i$

Ví dụ 2. Số phức 6 – i có phần thực là 6, phần ảo là – 1.

3. Số phức bằng nhau

– Định nghĩa : Hai số phức bằng nhau nếu phần thực và phần ảo của chúng tương ứng bằng nhau :

a + bi = c + di a = c và b = d.

Ví dụ 3. Tìm các số thực x và y biết :

(2x – 1) + (y – 2)i = 3 + (4 – y)i

Lời giải:

Ta có : (2x – 1) + (y – 2)i = 3 + (4 – y)i

$$\begin{gathered} \iff \left\{\begin{array}{c}2x-1=3\\ y-2=4-y\end{array}\right. \\ \iff \left\{\begin{array}{c}x=2\\ y=3\end{array}\right. \end{gathered}$$

Vậy x = 2 và y = 3.

– Chú ý :

a) Mỗi số thực a được coi là một số phức với phần ảo bằng 0: a = a + 0i.

Như vậy, mỗi số thực cũng là một số phức. Ta có : $R\subset C$.

b) Số phức 0 + bi được gọi là số thuần ảo và viết đơn giản là bi : bi = 0 + bi

Đặc biệt : i = 0 + 1.i

Số i được gọi là đơn vị ảo.

Ví dụ 4. Số phức z có phần thực là $-\frac{1}{2}$ và phần ảo là $\frac{1}{2}$ là $z=\frac{-1}{2}+\frac{1}{2}i$.

4. Biểu diễn hình học số phức

Điểm M(a ; b) trong một hệ tọa độ vuông góc của mặt phẳng được gọi là điểm biểu diễn số phức z = a + bi.

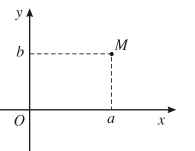
Ví dụ 5.

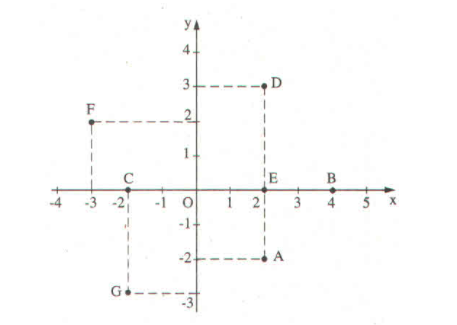
Điểm A biểu diễn số phức 2 – 2i

Điểm B biểu diễn số phức 4.

Điểm C biểu diễn số phức – 2.

Điểm D biểu diễn số phức 2 + 3i.

Điểm E biểu diễn số phức 2.

Điểm F biểu diễn số phức – 3 + 2i.

Điểm G biểu diễn số phức –2 – 3i.

5. Mô đun của số phức.

Giả sử số phức z = a + bi được biểu diễn bởi điểm M(a ; b) trên mặt phẳng tọa độ.

Độ dài của vecto $\overrightarrow{OM}$ được gọi là môđun của số phức z và kí hiệu là |z|.

Vậy $\left|z\right|=\left|\overrightarrow{OM}\right|$hay $\left|a+bi\right|=\left|\overrightarrow{OM}\right|$.

Ta thấy: $\left|a+bi\right|=\sqrt{a^2+b^2}$

Ví dụ 6.

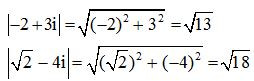
6. Số phức liên hợp

– Định nghĩa : Cho số phức z = a + bi. Ta gọi a – bi là số phức liên hợp của z và kí hiệu là $\overline{z}=a-bi$.

Ví dụ 7.

Nếu z = – 3 + 5i thì $\overline{z}=-3-5i$.

Nếu z = – 4 + 4i thì $\overline{z}=-4-4i$.

– Nhận xét :

+ Trên mặt phẳng tọa độ các điểm biểu diễn z và $\overline{z}$ đối xứng nhau qua trục Ox.

+ Từ định nghĩa ta có: $\overline{\overline{z}}=z;\left|\overline{z}\right|=\left|z\right|$.

B. Bài tập tự luyện

Bài 1. Tìm phần thực và phần ảo của số phức z, biết :

a) – 2 + 2i ;

b) $8-i\sqrt{3}$;

c) – 8 ;

d) – 10i.

Lời giải :

a) Phần thực là – 2; phần ảo là 2.

b) Phần thực là 8; phần ảo là $-\sqrt{3}$.

c) Ta có : – 8 = –8 + 0.i nên có phần thực là – 8; phần ảo là 0.

d) Ta có : –10i = 0 – 10i nên có phần thực là 0; phần ảo là –10.

Bài 2. Tìm các số thực x, y biết :

a) (6 – 3x) + (x – y)i = 3 + 2i;

b) (7 – y) + (x – 4)i = (y – 2).i

Lời giải :

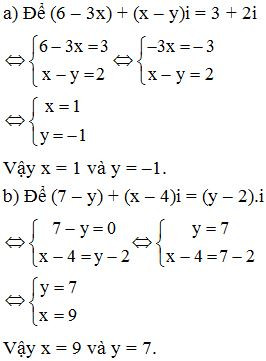
Bài 3. Tính $\left|z\right|$, với :

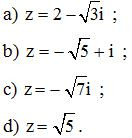
Lời giải :

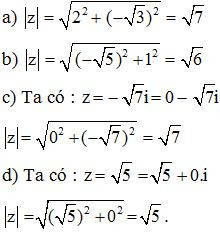
Bài 4. Tìm $\overline{z}$, biết :

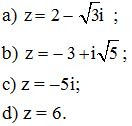
Lời giải:

a) Số phức liên hợp của z là $\overline{z}=2+\sqrt{3}i$;

b) Số phức liên hợp của z là $\overline{z}=-3-\text{\hspace{0.17em}}i\sqrt{5}$

c) Số phức liên hợp của z là $\overline{z}=5i$;

d) Số phức liên hợp của z là $\overline{z}=6$.

Trắc nghiệm Toán 12 Bài 1: Số phức

Câu 1: (Đề thi THPT Quốc gia năm 2017 – Mã đề 102) Cho số phức $z=1-i+i^3$. Tìm phần thực a và phần ảo b của z.

A. $a=0,b=1$.

B. $a=-2,b=1$.

C. $a=1,b=0$.

D. $a=1,b=-2$.

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có: $z=1-i+i^3=1-i-i$

$=1-2i$

$\Rightarrow a=1,b=-2$

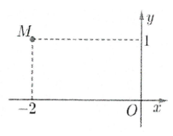
Câu 2: Điểm M trong hình vẽ bên là điểm biểu diễn số phức

A. $z=-2+i$

B. $z=1-2i$

C. $z=2+i$

D. $z=1+2i$

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có: M(-2; 1) $\Rightarrow z=-1+2i$

Câu 3: Trên tập số phức, $2x+y+\left(2y-x\right)i$$=x-2y+3+(y+2x+1)i$ với $x,y\in ℝ$. Tính giá trị của biểu thức $P=2x+3y$.

A. 7.

B. 3.

C. 1.

D. 4.

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có $\left\{\begin{array}{l}2x+y=x-2y+3\\ 2y-x=y+2x+1\end{array}\right.$

$\iff \{\begin{array}{l}x=0\\ y=1\end{array}$.

Câu 4: Tìm tất cả các số thực x, y thỏa mãn đẳng thức $x\left(3+5i\right)+y{\left(1-2i\right)}^3=-35+23i$

A. $\left(x;y\right)=\left(-3;4\right)$.

B. $\left(x;y\right)=\left(3;4\right)$.

C. $\left(x;y\right)=\left(3;-4\right)$.

D. $\left(x;y\right)=\left(-3;-4\right)$.

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có $3x+5xi+y\left(-11+2i\right)$

$=-35+23i$

$\iff \{\begin{array}{l}3x-11y=-35\\ 5x+2y=23\end{array}$

$\iff x=3;y=4$

Câu 5: Cho số phức $z={\left(2i\right)}^4-\frac{{\left(1+i\right)}^6}{5i}$. Số phức $\overline{5z+3i}$ là số phức nào sau đây?

A. $440+3i$.

B. $88+3i$.

C. $440-3i$.

D. $88-3i$.

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có: $z={\left(2i\right)}^4-\frac{{\left(1+i\right)}^6}{5i}$

$=16i^4-\frac{{\left(2i\right)}^3}{5i}=16-\frac{8}{5}{i}^2$

$=16+\frac{8}{5}=\frac{88}{5}$

Do đó $\overline{5z+3i}=\overline{88+3i}=88-3i$

Câu 6: Cho số phức $z=a+bi\left(a,b\in ℝ\right)$ thỏa $z=\left(1+2i\right)\left(3-i\right)$. Tính tổng $P=a+b$.

A. 6.

B. 10.

C. 5.

D. 0.

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có: $z=\left(1+2i\right)\left(3-i\right)=5+5i$

$\Rightarrow a=5,b=5\Rightarrow P=a+b=10$

Câu 7: Cho số thực x, y thỏa $2x+1+\left(1-2y\right)i=2\left(2-i\right)+yi-x$. Tính $T=x^2-3xy-y$.

A. -1.

B. 1.

C. -2.

D. -3.

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có $\left\{\begin{array}{l}2x+1=4-x\\ 1-2y=-2+y\end{array}\right.$

$\iff x=y=1$

Khi đó T = 1 – 3.1.1 – 1 = - 3.

Câu 8: (Đề minh họa lần 2 – Bộ GDĐT năm 2017) Điểm M trong hình vẽ bên là điểm biểu diễn số phức z. Tìm phần thực và phần ảo của z.

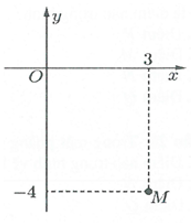
A. Phần thực là -4 và phần ảo là 3.

B. Phần thực là 3 và phần ảo là -4i.

C. Phần thực là 3 và phần ảo là -4.

D. Phần thực là -4 và phần ảo là 3i.

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có: $M\left(3;-4\right)\Rightarrow z=3-4i$

$\Rightarrow$ phần thực là 3 và phần ảo là -4

Câu 9: Tìm phần thực và phần ảo của số phức liên hợp $\overline{z}$ của số phức $z=-i\left(4i+3\right)$.

A. Phần thực là 4 và phần ảo bằng -3

B. Phần thực là 4 và phần ảo bằng 3

C. Phần thực là 4 và phần ảo bằng 3i

D. Phần thực là -4 và phần ảo bằng 3i

Hiển thị đáp án

Đáp án: B

Giải thích:

Số phức $z=4-3i$

$\Rightarrow \overline{z}=4+3i$ có phần thực là 4 và phần ảo bằng 3.

Câu 10: Cho số phức $z=3-2i$. Tìm phần ảo b của số phức liên hợp của z.

A. $b=2i$.

B. $b=-2i$.

C. $b=2$.

D. $b=-2$.

Hiển thị đáp án

Đáp án: C

Giải thích:

Số phức liên hợp của z là $\overline{z}=3+2i$

$\Rightarrow$ phần ảo $b=2$.

Xem thêm các bài tổng hợp lý thuyết Toán lớp 12 đầy đủ, chi tiết khác:

Lý thuyết Cộng, trừ và nhân số phức

Lý thuyết Phép chia số phức

Lý thuyết Phương trình bậc hai với hệ số thực

Lý thuyết Ôn tập chương 4

Lý thuyết Khái niệm về khối đa diện