Lý thuyết Ôn tập chương 1 (mới 2024 + Bài Tập) – Toán 12
Lý thuyết Ôn tập chương 1 lớp 12 gồm lý thuyết chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm Toán 12 Ôn tập chương 1.
Lý thuyết Toán 12 Ôn tập chương 1
A. Lý thuyết
1. Khối lăng trụ và khối chóp.
- Khối chóp là phần không gian được giới hạn bởi một hình chóp kể cả hình chóp ấy.
Khối chóp cụt là phần không gian được giới hạn bởi một hình chóp cụt kể cả hình chóp cụt ấy.
- Khối lăng trụ là phần không gian được giới hạn bởi một hình lăng trụ kể cả hình lăng trụ ấy.
- Tên của khối lăng trụ hay khối chóp được đặt theo tên của hình lăng trụ hay hình chóp giới hạn nó.
Ví dụ. Ứng với hình lăng trụ tứ giác ABCD.EFGH ta có khối lăng trụ tứ giác ABCD.EFGH; ứng với hình chóp tứ giác S.ABCD ta có khối chóp tứ giác S.ABCD.
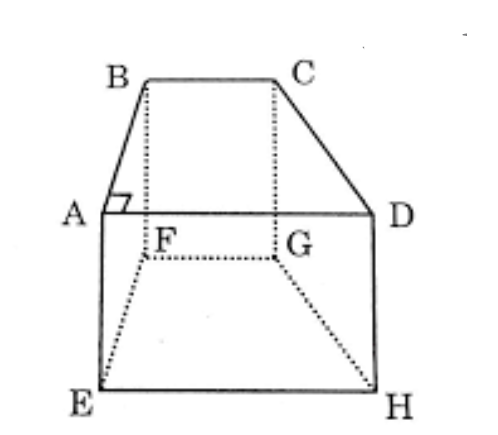
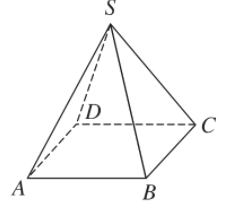
- Ta gọi đỉnh, cạnh, mặt, mặt bên, mặt đáy, cạnh đáy, cạnh bên… của một hình lăng trụ (hình chóp hay hình chóp cụt) theo thứ tự là đỉnh; cạnh, mặt, mặt bên, mặt đáy, cạnh đáy, cạnh bên… của khối lăng trụ (khối chóp hay khối chóp cụt) tương ứng.
- Điểm không thuộc khối lăng trụ được gọi là điểm ngoài của khối lăng trụ, điểm thuộc khối lăng trụ nhưng không thuộc hình lăng trụ ứng với khối lăng trụ đó được gọi là điểm trong của khối lăng trụ. Điểm trong hay điểm ngoài của khối chóp, khối chóp cụt cũng được định nghĩa tương tự.
2. Khái niệm về hình đa diện và khối đa diện
2.1 Khái niệm về hình đa diện
Hình đa diện (gọi tắt là đa diện) là hình được tạo bởi một số hữu hạn các đa giác thỏa mãn hai tính chất sau:
a) Hai đa giác phân biệt chỉ có thể hoặc không có điểm chung, hoặc chỉ có một đỉnh chung, hoặc chỉ có một cạnh chung.
b) Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.
- Các đỉnh, cạnh của các đa giác ấy theo thứ tự gọi là đỉnh, cạnh của hình đa diện.
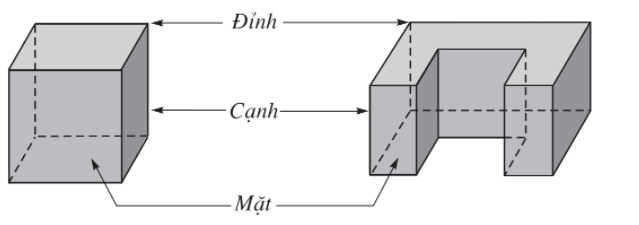
2.2 Khái niệm về khối đa diện
- Khối đa diện là phần không gian được giới hạn bởi một hình đa diện, kể cả hình đa diện đó.
- Những điểm không thuộc khối đa diện được gọi là điểm ngoài của khối đa diện. Những điểm thuộc khối đa diện nhưng không thuộc hình đa diện giới hạn khối đa diện ấy được gọi là điểm trong của khối đa diện.
Tập hợp các điểm trong được gọi là miền trong, tập hợp các điểm ngoài được gọi là miền ngoài của khối đa diện.
- Mỗi hình đa diện chia các điểm còn lại của không gian thành hai miền không giao nhau là miền trong và miền ngoài của hình đa diện, trong đó chỉ có miền ngoài là chứa hoàn toàn một đường thẳng nào đấy.
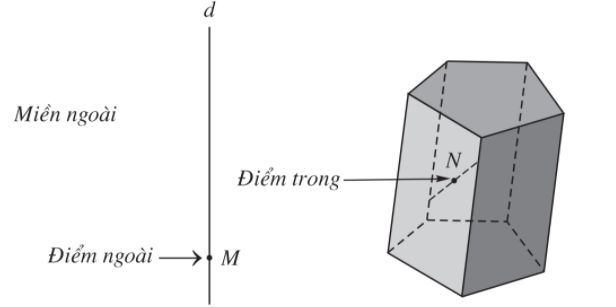
Ví dụ.
- Các hình dưới đây là những khối đa diện
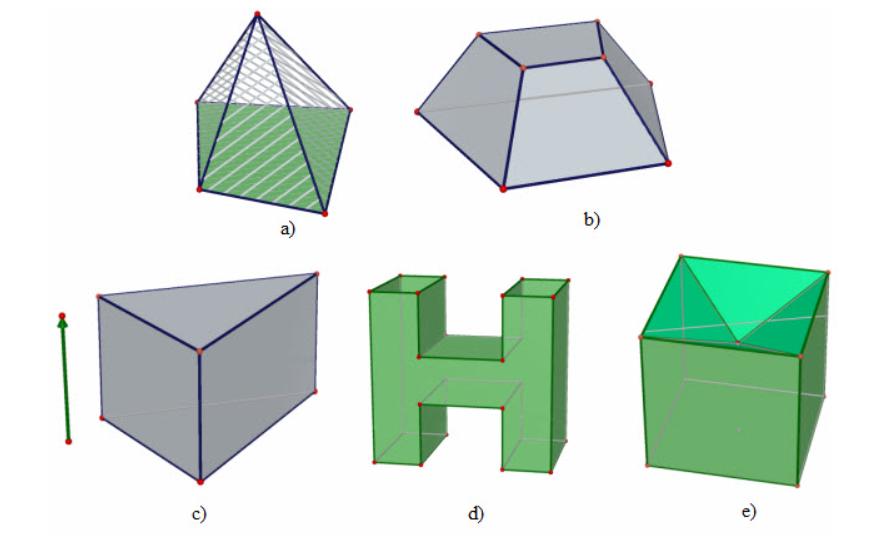
- Các hình dưới đây không phải là những khối đa diện.
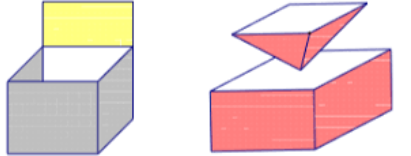
3. Hai đa diện bằng nhau.
3.1 Phép dời hình trong không gian.
- Trong không gian, quy tắc đặt tương ứng mỗi điểm M với điểm M’ xác định duy nhất được gọi là một phép biến hình trong không gian.
- Phép biến hình trong không gian được gọi là phép dời hình nếu nó bảo toàn khoảng cách giữa hai điểm tùy ý.
- Ví dụ. Trong không gian, các phép biến hình sau đây gọi là phép dời hình :
a) Phép tịnh tiến theo vectơ , là phép biến hình, biến mỗi điểm M thành điểm M’ sao cho .
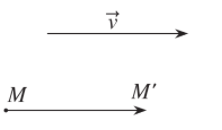
b) Phép đối xứng qua mặt phẳng (P), là phép biến hình biến mỗi điểm thuộc (P) thành chính nó, biến mỗi điểm M không thuộc (P) thành điểm M’ sao cho (P) là mặt phẳng trung trực của MM’.
Nếu phép đối xứng qua mặt phẳng (P) biến hình (H) thành chính nó thì (P) được gọi là mặt phẳng đối xứng của (H).
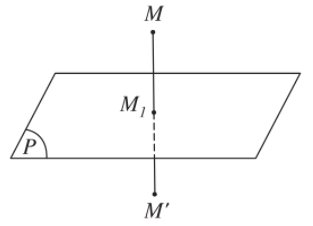
c) Phép đối xứng tâm O, là phép biến hình biến điểm O thành chính nó, biến mỗi điểm M khác O thành điểm M’ sao cho O là trung điểm của MM’.
Nếu phép đối xứng tâm O biến hình (H) thành chính nó thì O được gọi là tâm đối xứng của (H).
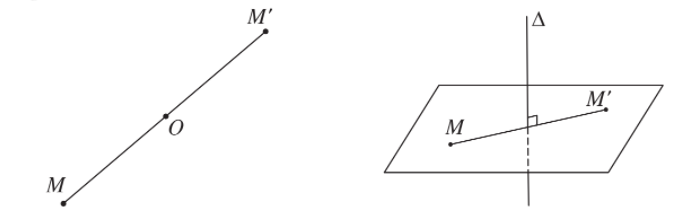
d) Phép đối xứng qua đường thẳng ∆ (hay phép đối xứng qua trục ∆) là phép biến hình biến mọi điểm thuộc đường thẳng ∆ thành chính nó, biến mỗi điểm M không thuộc ∆ thành điểm M’ sao cho ∆ là đường trung trực của MM’.
Nếu phép đối xứng qua đường thẳng ∆ biến hình (H) thành chính nó thì ∆ gọi là trục đối xứng của (H) .
Nhận xét:
+ Thực hiện liên tiếp các phép dời hình sẽ được một phép dời hình.
+ Phép dời hình biến đa diện (H) thành đa diện (H’), biến đỉnh, cạnh, mặt của (H) thành đỉnh, cạnh, mặt tương ứng của (H’).
3.2 Hai hình bằng nhau
- Hai hình được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.
Đặc biệt, hai đa diện được gọi là bằng nhau nếu có một phép dời hình biến đa diện này thành đa diện kia.
- Ví dụ. Phép đối xứng tâm O biến đa diện (H) thành đa diện (H’). Phép đối xứng trục ∆, biến đa diện (H’) thành đa diện (H”). Do đó, phép dời hình có được bằng cách thực hiện liên tiếp hai phép dời hình trên biến hình (H) thành hình (H”) .
Từ đó, suy ra các hình (H); (H’) và (H”) là bằng nhau.
4. Phân chia và lắp ghép các khối đa diện
Nếu khối đa diện (H) là hợp của hai khối đa diện (H1) và (H2) sao cho (H1) và (H2) không có chung điểm trong nào thì ta nói có thể chia được khối đa diện (H) thành hai khối đa diện (H1) và (H2), hay có thể lắp ghép hai khối đa diện (H1) và (H2) với nhau để được khối đa diện (H).
- Ví dụ. Với khối chóp tứ giác S.ABCD, ta hãy xét hai khối chóp tam giác S.ABC và S.ACD.
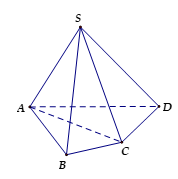
Ta thấy rằng:
+ Hai khối chóp S.ABC và S.ACD không có điểm trong chung.
+ Hợp của hai khối chóp S.ABC và S.ACD chính là khối chóp S.ABCD.
Vậy khối chóp S.ABCD được phân chia thành hai khối chóp tam giác là S.ABC và S.ACD .
- Nhận xét. Một khối đa diện bất kì luôn có thể phân chia thành những khối tứ diện.
5. Khối đa diện lồi.
Khối đa diện lồi (H) được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kì của (H) luôn thuộc (H). Khi đó đa diện xác định (H) được gọi là đa diện lồi.
Ví dụ. Các khối chóp tam giác, tứ giác, các khối lăng trụ tam giác, khối lăng trụ tứ giác… đều là những khối đa diện đều.
- Người ta chứng minh được rằng, một khối đa diện là khối đa diện lồi khi và chỉ khi miềm trong của nó luôn nằm về một phía đối với mỗi mặt phẳng chứa một mặt của nó.
6. Khối đa diện đều.
- Định nghĩa: Khối đa diện đều là khối đa diện lồi có tính chất sau đây:
a) Mỗi mặt của nó là một đa giác đều p cạnh.
b) Mỗi đỉnh của nó là đỉnh chung của đúng q mặt.
Khối đa diện đều như vậy được gọi là khối đa diện đều loại {p; q}.
Từ định nghĩa trên ta thấy các mặt của khối đa diện đều là những đa giác đều bằng nhau.
- Định lí: Chỉ có năm loại khối đa diện đều. Đó là các loại {3; 3}; loại {4; 3}; loại {3; 4}; loại {5; 3} và loại {3; 5}.
Tùy theo số mặt của chúng, năm loại khối đa diện đều kể trên theo thứ tự gọi là các khối tứ diện đều, khối lập phương, khối bát diện đều (hay khối tám mặt đều), khối mười hai mặt đều và khối hai mươi mặt đều.
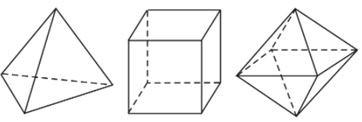
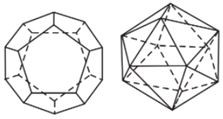
Bảng tóm tắt của năm loại khối đa diện đều.
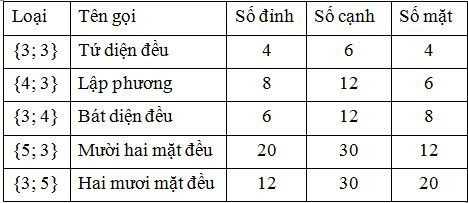
Ví dụ. Chứng minh rằng nếu khối đa diện có các mặt là những tam giác thì tổng các mặt của nó phải là một số chẵn.
Lời giải:
Gọi số cạnh và số mặt của đa diện lần lượt là c và m .
Vì mỗi mặt có ba cạnh và mỗi cạnh là cạnh chung của đúng hai mặt nên ta có số cạnh của đa diện là
Do đó, 3m chia hết cho 2 mà 3 không chia hết cho 2 nên m phải chia hết cho 2, nghĩa là m là số chẵn.
Vậy nếu khối đa diện có các mặt là những tam giác thì tổng các mặt của nó phải là một số chẵn.
7. Khái niệm về thể tích của khối đa diện
Người ta chứng minh được rằng: có thể đặt tương ứng cho mỗi khối đa diện (H) một số dương duy nhất V(H) thỏa mãn các tính chất sau:
a) Nếu (H) là khối lập phương có cạnh bằng 1 thì V(H) = 1.
b) Nếu hai khối đa diện (H1) và (H2) bằng nhau thì V(H1) = V(H2).
c) Nếu khối đa diện (H) được phân chia thành hai khối đa diện (H1) và (H2) thì:
V(H) = V(H1) + V(H2).
Số dương V(H) nói trên được gọi là thể tích của khối đa diện (H). Số đó cũng được gọi là thể tích của hình đa diện giới hạn khối đa diện (H).
Khối lập phương có cạnh bằng 1 được gọi là khối lập phương đơn vị.
- Định lí : Thể tích của khối hình chữ nhật bằng tích ba kích thước của nó.
8. Thể tích của khối lăng trụ.
Định lí: Thể tích khối lăng trụ có diện tích đáy B và chiều cao h là: V = B.h
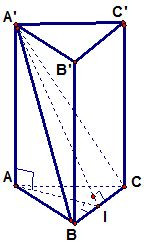
Ví dụ. Đáy của lăng trụ đứng tam giác ABC.A’B’C’ là tam giác đều cạnh a = 4 và biết diện tích tam giác A’BC bằng 8. Tính thể tích khối lăng trụ.
Lời giải:

9. Thể tích khối chóp.
Định lí. Thể tích khối chóp có diện tích đáy B và chiều cao h là: .
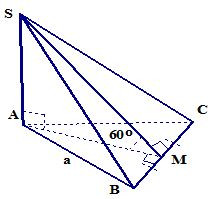
Ví dụ. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a biết SA vuông góc với đáy ABC và (SBC) hợp với đáy (ABC) một góc 60o. Tính thể tích hình chóp.
Lời giải:

B. Bài tập tự luyện
Bài 1. Cho các hình sau:
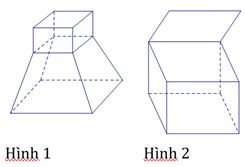
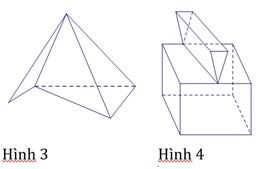
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình nào là đa diện?
Lời giải:
Trong các hình trên chỉ có hình 1 là hình đa diện.
Vì hình 1 là hình được tạo bởi một số hữu hạn các đa giác thỏa mãn hai tính chất sau:
a) Hai đa giác phân biệt chỉ có thể hoặc không có điểm chung, hoặc chỉ có một đỉnh chung, hoặc chỉ có một cạnh chung.
b) Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.
Bài 2. Hãy phân chia khối lập phương ABCD.A’B’C’D’ thành 5 khối tứ diện?
Lời giải:
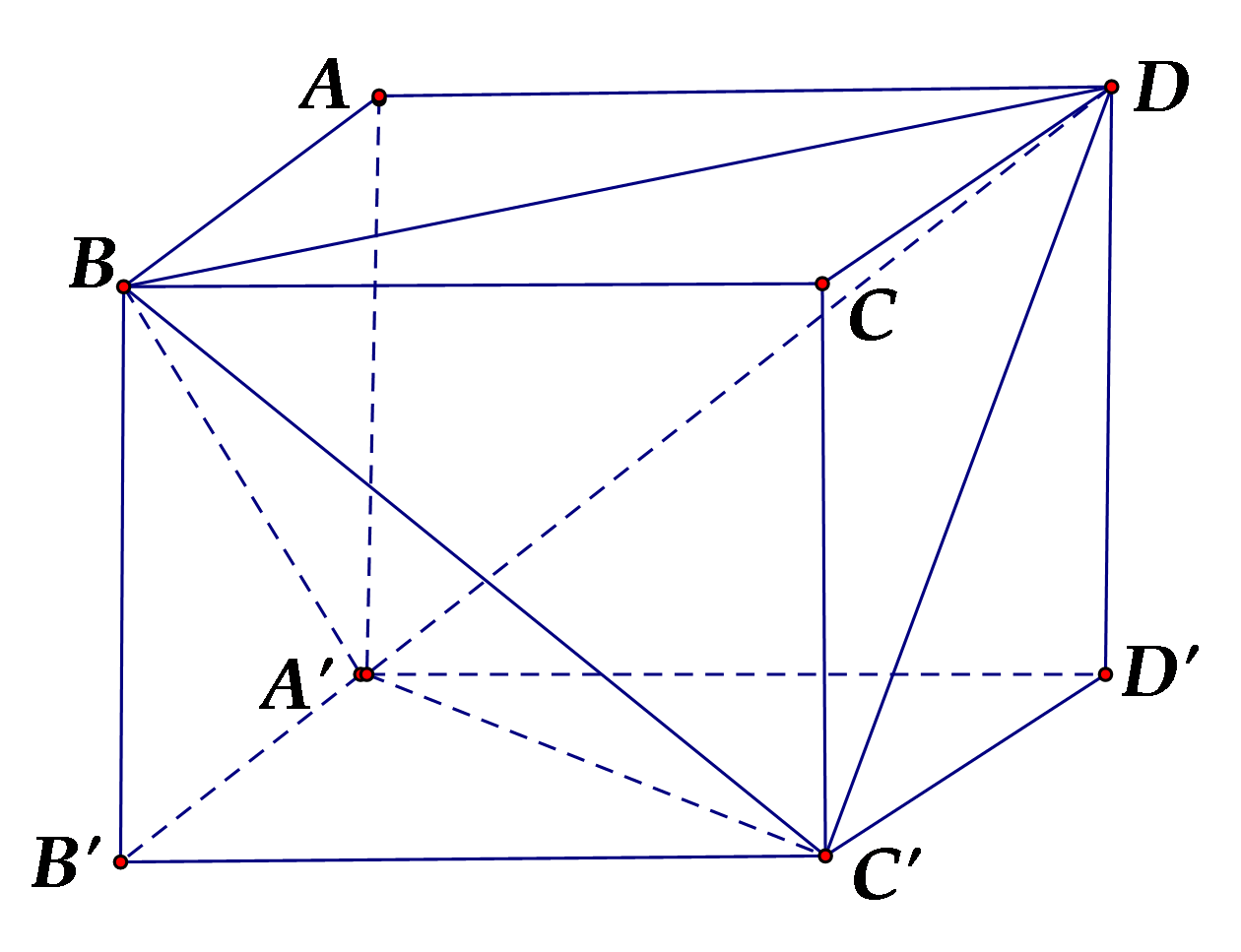
Với hình lập phương ABCD.A’B’C’D’ ta có thể phân chia thành 5 khối tứ diện sau:
DA’D’C’; A’ABD; C’BCD; BA’B’C’ và BDCA’
Bài 3. Cho hình lập phương ABCD.A’B’C’D’.
a) Chứng minh rằng các hình chóp A.A’B’C’D’ và C’.ABCD là bằng nhau.
b) Chứng minh rằng các hình lăng trụ ABC.A’B’C’ và AA’D’.BB’C’ bằng nhau.
Lời giải:
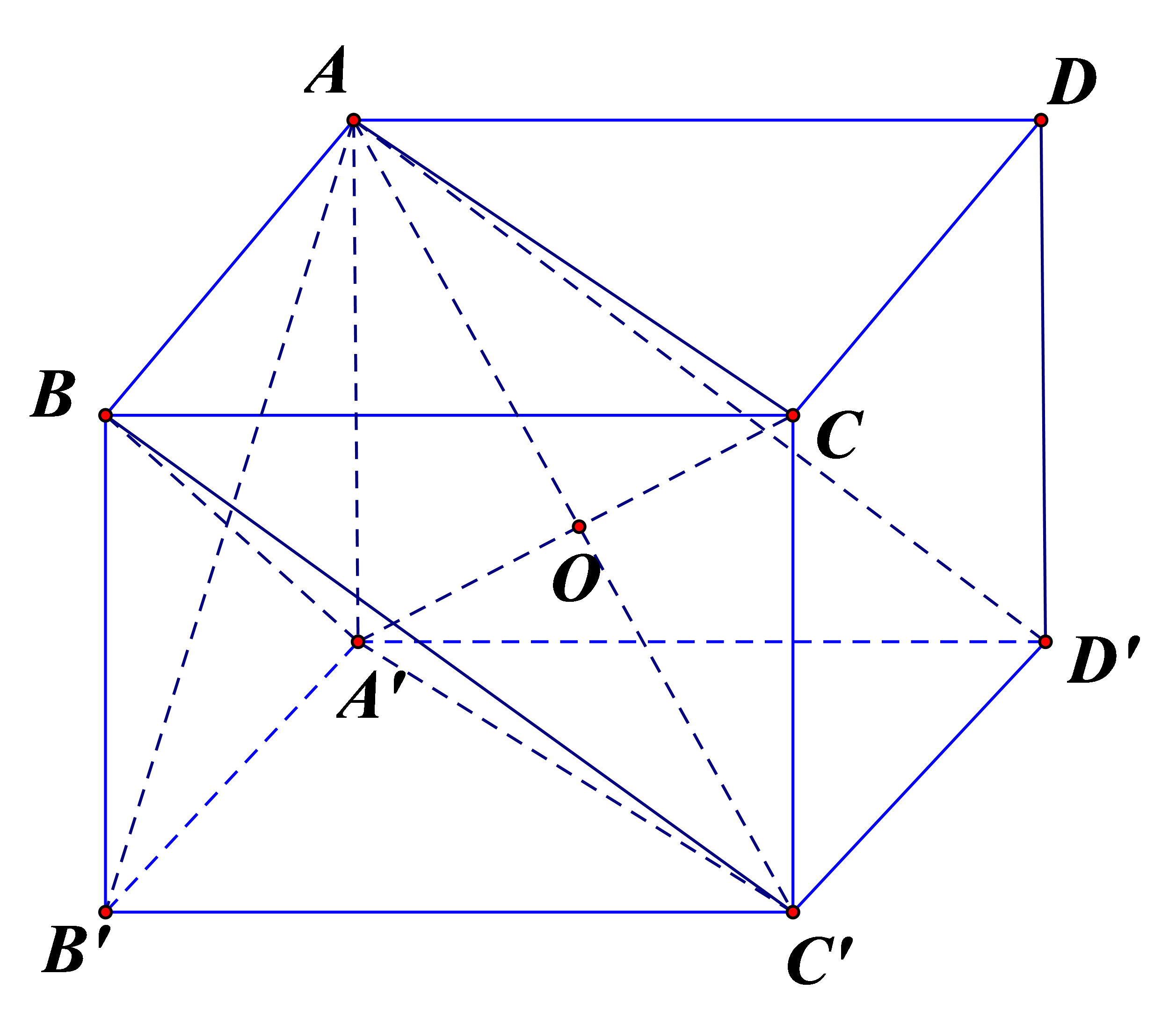
Gọi O là tâm của hình lập phương.
a) Các hình chóp A.A’B’C’D’ và C’.ABCD bằng nhau vì qua phép đối xứng tâm O, hình chóp A.A’B’C’D’ biến thành hình chóp C’.CDAB (hay chính là hình chóp C’.ABCD).
b) Các hình lăng trụ ABC.A’B’C’ và AA’D’.BB’C’ bằng nhau vì qua phép đối xứng qua mặt phẳng (AB’C’D) thì hình lăng trụ ABC.A’B’C’ biến thành hình lăng trụ AA’D’.BB’C’.
Bài 4. Cho bốn hình sau, hỏi có bao nhiêu hình đa diện lồi?


Lời giải:
Trong bốn hình đã cho thì chỉ có hình 3 là hình đa diện lồi.
Bài 5. Cho khối tứ diện đều ABCD. Chứng ming rằng:
a) Trọng tâm các mặt của khối chóp đó là 4 đỉnh của 1 tứ diện đều.
b) Các trung điểm các cạnh của khối đó là các đỉnh của một khối tám mặt đều.
Lời giải:
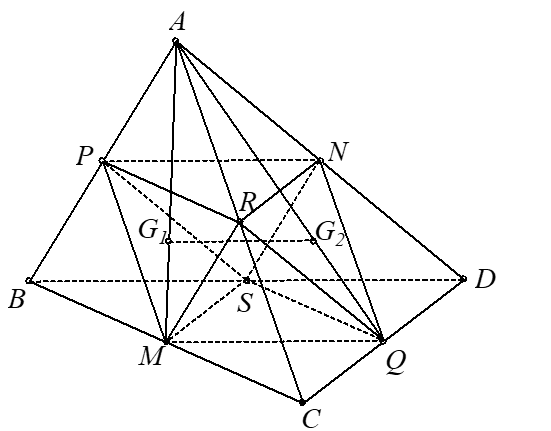
a) Gọi Q và M lần lượt là trung điểm của CD; CB.
Gọi G1; G2; G3; G4 lần lượt là trọng tâm các tam giác ABC; ACD; ABD và BCD
Gọi a là độ dài cạnh của tứ diện, ta có
Tương tự; G1G4 = G1G3 = G2G3 = G2G4 = G3G4 = nên G1G2G3G4 là một tứ diện đều cạnh .
b) Gọi N; P; R; S lần lượt là trung điểm các cạnh AD; AB; AC; BD
Theo tính chất đường trung bình, ta có:
QM = QN = QS = QR = PM = PN = PS = PR =
Do đó các trung điểm các cạnh của khối đó là các đỉnh của một khối tám mặt đều.
Bài 6. Chứng minh rằng tâm các mặt của hình lập phương là các đỉnh của một bát diện đều.
Lời giải:
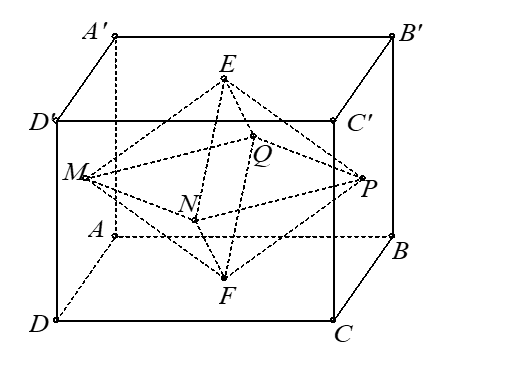
Cho hình lập phương ABCD.A’B’C’D’.
Giả sử độ dài cạnh của hình lập phương ABCD.A’B’C’D’ là a.
Gọi M; N; P; Q; E; F lần lượt là tâm các mặt của hình lập phương.
Ta có:
Tương tự ta tính được:
MP = MQ = ME = MF = NP = NQ = NE
= NF = PQ = PE = PF= QE = QF = EF =
Do đó, MNPQEF là một bát diện đều.
Bài 7. Cho lăng trụ tứ giác đều ABCD.A’B’C’D' có cạnh bên bằng 4a và đường chéo 5a. Tính thể tích khối lăng trụ này.
Lời giải:
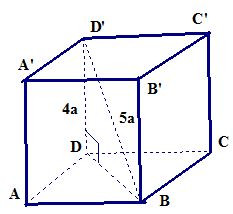
Vì ABCD.A'B'C'D' là lăng trụ đứng nên tam giác BDD’ vuông tại D, ta có:
BD2 = BD'2 - DD'2 = 9a2
Suy ra : BD = 3a
Vì ABCD là hình vuông
Suy ra diện tích đáy ABCD : SABCD
Vậy thể tích khối lăng trụ ABCD.A’B’C’D’ là:
V = B.h = SABCD.AA' = 9a3.
Bài 8. Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh a. Mặt bên SAB là tam giác đều nằm trong mặt phẳng vuông góc với đáy ABCD. Tính thể tích khối chóp S.ABCD.
Lời giải:
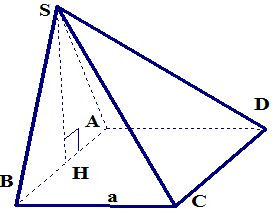

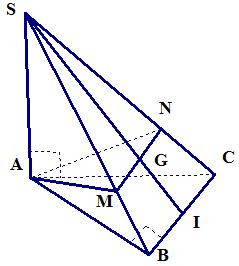
Bài 9. Cho hình chóp S.ABC có tam giác ABC vuông cân ở B, , SA vuông góc với đáy ABC, SA = a.
a) Tính thể tích của khối chóp S.ABC.
b) Gọi G là trọng tâm tam giác ABC, mặt phẳng (α) qua AG và song song với BC cắt SC, SB lần lượt tại M, N. Tính thể tích của khối chóp S.AMN.
Lời giải:

Trắc nghiệm Toán 12 Bài Ôn tập Chương 1 - Khối đa diện
Câu 1. Khối lăng trụ đáy là hình chữ nhật có hai kích thước lần lượt là 2a, 3a, chiều cao khối lăng trụ là 5a. Tính thể tích khối lăng trụ:
A.
B.
C.
D.
Đáp án: A
Giải thích:
Diện tích đáy của khối lăng trụ đã cho là:
Thể tích khối lăng trụ đã cho là:
Câu 2. Cho khối lăng trụ ABC.A’B’C’, khoảng cách từ C đến đường thẳng BB’ bằng , khoảng cách từ A đến các đường thẳng BB’ và CC’ lần lượt bằng 1 và 2, hình chiếu vuông góc của A lên mặt phẳng là trung điểm M của B’C’ và . Thể tích của khối lăng trụ đã cho bằng:
A.
B.
C.
D.
Đáp án: B
Giải thích:
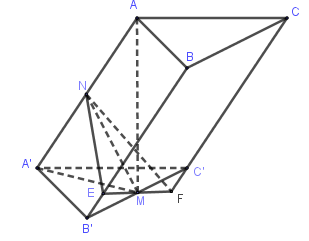
Qua M dựng mặt phẳng (P) vuông góc với AA’ cắt các cạnh AA’, BB’, CC’ lần lượt tại N, E, F.
Ta có:
Có:
vuông tại N (định lí Pitago)
Xét tam giác AA’M vuông tại M, ta có:
Ta có:
Ta thấy là hình chiếu vuông góc của lên mặt phẳng (P)
Câu 3. Cho tứ diện đều ABCD có cạnh bằng 3. Gọi M, N là hai điểm thay đổi lần lượt thuộc cạnh BC, BD sao cho mặt phẳng (AMN) luôn vuông góc với mặt phẳng (BCD). Gọi lần lượt là giá trị lớn nhất và nhỏ nhất của thể tích khối tứ diện ABMN. Tính ?
A.
B.
C.
D.
Đáp án: A
Giải thích:
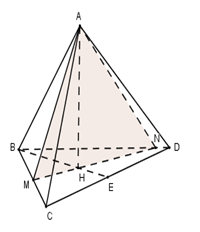
Tứ diện ABCD đều, gọi H là tâm tam giác đều
Có
với AH không đổi.
Dễ thấy diện tích tam giác BMN nhỏ nhất khi và chỉ khi tam giác BMN đều, khi đó
Diện tích BMN lớn nhất khi và chỉ khi , khi đó:
Câu 4. Thể tích của khối hộp chữ nhật có ba kích thước lần lượt là 1, 2, 3 bằng:
A. 2
B. 3
C. 1
D. 6
Đáp án: D
Giải thích: Hình hộp chữ nhật có 3 kích thước lần lượt 1, 2, 3 là: V = 1.2.3 = 6
Câu 5. Khối chóp tam giác có độ dài 3 cạnh xuất phát từ một đỉnh là a, 2a, 3a có thể tích lớn nhất bằng:
A.
B.
C.
D.
Đáp án: C
Giải thích:
Xét khối chóp tam giác S.ABC,
có
và h là khoảng cách từ C đến (SAB)
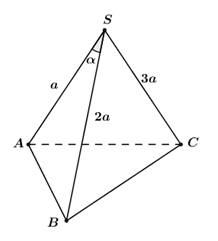
Khi đó, thể tích khối chóp S.ABC là
(1)
Diện tích tam giác SAB là
(2)
Từ (1) và (2) suy ra:
mà
Dầu “=” xảy ra khi
hay hình chóp S.ABC là tứ diện vuông đỉnh S.
Câu 6. Khối hộp chữ nhật có các kích thước lần lượt là a, 2a, 3a có thể tích bằng:
A.
B.
C.
D.
Đáp án: B
Giải thích:
Thể tích khối hộp chữ nhật là
Câu 7. Cho khối lăng trụ tam giác có thể tích V. Trên đáy A’B’C’ lấy điểm M bất kì. Thể tích khối chóp M.ABC tính theo V bằng:
A.
B.
C.
D.
Đáp án: C
Giải thích:
Vì
Câu 8. Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a và , AB’ hợp với đáy (ABCD) một góc . Thể tích của khối hộp là:
A.
B.
C.
D.
Đáp án: A
Giải thích:
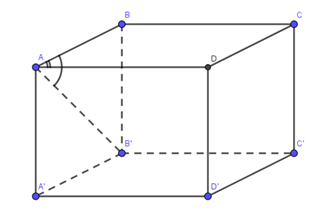
ABCD.’B’C’D’ là hình hộp đứng
Tam giác ABB’ vuông tại B
Tam giác ABD có:
tam giác ABD đều, có cạnh đều bằng a.
Thể tích khối hộp ABCD.A’B’C’D’:
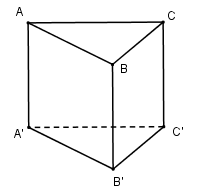
Câu 9. Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại A. . Thể tích khối lăng trụ ABC.A’B’C’ là:
A.
B.
C.
D.
Đáp án: A
Giải thích:
Câu 10. Cho khối lập phương có thể tích bằng 27, diện tích toàn phần của khối lập phương đã cho bằng:
A. 75
B. 36
C. 18
D. 54
Đáp án: D
Giải thích:
Cạnh của khối lập phương đã cho là: diện tích toàn phần của khối lập phương đã cho là: 6.32 = 54
Xem thêm các bài tổng hợp lý thuyết Toán lớp 12 đầy đủ, chi tiết khác:
Lý thuyết Khái niệm về mặt tròn xoay
Xem thêm các chương trình khác:
- Giải sgk Hóa học 12 (sách mới) | Giải bài tập Hóa 12
- Lý thuyết Hóa học 12
- Giải sbt Hóa học 12
- Các dạng bài tập Hoá học lớp 12
- Giáo án Hóa học lớp 12 mới nhất
- Tóm tắt tác phẩm Ngữ văn 12
- Soạn văn 12 (hay nhất) | Để học tốt Ngữ văn 12 (sách mới)
- Soạn văn 12 (ngắn nhất)
- Tác giả tác phẩm Ngữ văn lớp 12
- Văn mẫu lớp 12
- Giải sgk Sinh học 12 (sách mới) | Giải bài tập Sinh học 12
- Lý thuyết Sinh học 12 | Kiến thức trọng tâm Sinh 12
- Giải sgk Địa Lí 12 (sách mới) | Giải bài tập Địa lí 12
- Lý thuyết Địa Lí 12
- Giải Tập bản đồ Địa Lí 12
- Giải sgk Vật Lí 12 (sách mới) | Giải bài tập Vật lí 12
- Giải sbt Vật Lí 12
- Lý thuyết Vật Lí 12
- Các dạng bài tập Vật lí lớp 12
- Giáo án Vật lí lớp 12 mới nhất
- Giải sgk Lịch sử 12 (sách mới) | Giải bài tập Lịch sử 12
- Giải Tập bản đồ Lịch sử 12
- Lý thuyết Lịch sử 12
- Giải sgk Giáo dục công dân 12
- Lý thuyết Giáo dục công dân 12
- Giải sgk Giáo dục quốc phòng - an ninh 12 (sách mới) | Giải bài tập GDQP 12
- Lý thuyết Giáo dục quốc phòng 12 | Kiến thức trọng tâm GDQP 12
- Lý thuyết Tin học 12
- Lý thuyết Công nghệ 12
