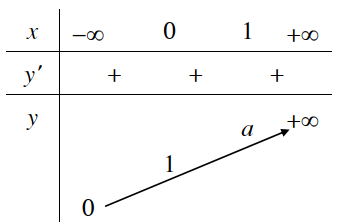Lý thuyết Ôn tập chương 2 (năm 2024 + Bài Tập) – Toán 12

Lý thuyết Toán 12 Ôn tập chương 2

A. Lý thuyết

1. Khái niệm lũy thừa

1.1 Lũy thừa với số mũ nguyên

Cho n là một số nguyên dương.

Với a là số thực tùy ý, lũy thừa bậc n của a là tích của n thừa số a.

aⁿ = a.a.a… a (n thừa số a)

Với a ≠ 0, ta có: a⁰ = 1 và $a^{-n}=\frac{1}{a^n}$

Trong biểu thức a^m ; ta gọi a là cơ số, số nguyên m là số mũ.

– Chú ý:

0⁰ và 0^–n không có nghĩa.

Lũy thừa với số mũ nguyên có các tính chất tương tự của lũy thừa với số mũ nguyên dương.

Ví dụ. Tính giá trị biểu thức:

$A={\left(\frac{1}{2}\right)}^{-3}.8+4^{-2}.2^4+{\left(\frac{1}{3}\right)}^{-3}.\frac{1}{27}$

Lời giải:

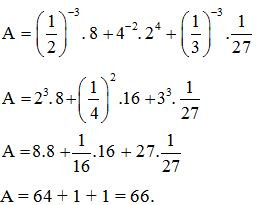
1.2 Phương trình xⁿ = b.

Đồ thị của hàm số y = x^{2k + 1} có dạng tương tự đồ thị hàm số y = x³ và đồ thị hàm số y = x^2k có dạng tương tự đồ thị hàm số y = x⁴.

Từ đó, ta có kết quả biện luận số nghiệm của phương trình xⁿ = b như sau:

a) Trường hợp n lẻ:

Với mọi số thực b, phương trình có nghiệm duy nhất.

b) Trường hợp n chẵn:

Với b < 0, phương trình vô nghiệm.

Với b = 0 , phương trình có một nghiệm x = 0.

Với b > 0, phương trình có hai nghiệm đối nhau.

1.3 Căn bậc n

a) Khái niệm: Cho số thực b và số nguyên dương n $(n\ge 2)$. Số a được gọi là căn bậc n của số b nếu aⁿ = b.

Ví dụ. Căn bậc ba của 27 là 3.

Căn bậc bốn của 256 là 4 và – 4.

– Từ định nghĩa và kết quả biện luận về số nghiệm của phương trình xⁿ = b; ta có:

Với n lẻ và $b\in ℝ$: Có duy nhất một căn bậc n của b, kí hiệu là $\sqrt[n]{b}$.

Với n chẵn và :

+ b < 0 : không tồn tại căn bậc n của b.

+ b = 0: có một căn bậc n của b là số 0.

+ b > 0: có hai căn trái dấu; kí hiệu giá trị dương là $\sqrt[n]{b}$; còn giá trị âm là $-\sqrt[n]{b}$.

b) Tính chất của căn bậc n

Từ định nghĩa ta có các tính chất sau:

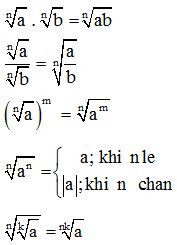
Ví dụ. Rút gọn các biểu thức:

a) $\sqrt[3]{9}.\sqrt[3]{-3}$;

b) $\sqrt[4]{{(-5)}^4}$.

Lời giải:

a) $\sqrt[3]{9}.\sqrt[3]{-3}$

$$\begin{gathered} =\sqrt[3]{9.(-3)} \\ =\sqrt[3]{-27} \\ =-3 \end{gathered}$$

b) $\sqrt[4]{{(-5)}^4}=\left|-5\right|=5$

1.4 Lũy thừa với số mũ hữu tỉ.

– Cho số thực a dương và số hữu tỉ $r=\frac{m}{n}$; trong đó $m\in \mathbb{Z};n\in \mathbb{N};$ $\hspace{0.17em}n\ge 2$. Lũy thừa của a với số mũ r là số a^r xác định bởi: $a^r=a^{\frac{m}{n}}=\sqrt[n]{a^m}$

Ví dụ.

$\begin{array}{l}{27}^{\frac{1}{3}}=\sqrt[3]{27}=3.\\ 9^{\frac{3}{2}}=\sqrt{9^3}=27\end{array}$

1.5 Lũy thừa với số mũ vô tỉ.

Cho a là một số dương, α là một số vô tỉ. Ta thừa nhận rằng, luôn có một dãy số hữu tỉ (r_n) có giới hạn là α và dãy số tương ứng $\left(a^{r_n}\right)$ có giới hạn không phụ thuộc vào việc chọn dãy số (r_n).

– Ta gọi giới hạn của dãy số $\left(a^{r_n}\right)$ là thừa số của a với số mũ α, kí hiệu là a^α.

$a^{\alpha }=\underset{n\to +\infty }{\lim }{a}^{r_n}$ với $\alpha =\underset{n\to +\infty }{\lim }{r}_n$.

– Chú ý: Từ định nghĩa, ta có: $1^{\alpha }=1 (\alpha \in ℝ)$.

2. Tính chất lũy thừa với số mũ thực.

Cho a; b là những số thực dương, α, β là những số thực tùy ý. Khi đó, ta có:

$\begin{array}{l}{a}^{\alpha }.a^{\beta }=a^{\alpha +\beta }\\ \frac{a^{\alpha }}{a^{\beta }}=a^{\alpha -\beta }\end{array}$

$\begin{array}{l}{\left(a^{\alpha }\right)}^{\beta }=a^{\alpha .\beta }\\ {\left(ab\right)}^{\alpha }=a^{\alpha }.b^{\alpha }\\ {\left(\frac{a}{b}\right)}^{\alpha }=\frac{a^{\alpha }}{b^{\alpha }}\end{array}$

Nếu a > 1 thì $a^{\alpha }>a^{\beta }$ khi và chỉ khi α > β.

Nếu a < 1 thì $a^{\alpha }>a^{\beta }$ khi và chỉ khi α < β.

Ví dụ. Rút gọn biểu thức:

$A=\frac{a^{\sqrt{5}+\text{\hspace{0.17em}}2}.a^{4-\sqrt{5}}}{{\left(a^{\sqrt{3}-1}\right)}^{\sqrt{3}+1}}$ với a > 0.

Lời giải:

Với a > 0 ta có:

$A=\frac{a^{\sqrt{5}+\text{\hspace{0.17em}}2}.a^{4-\sqrt{5}}}{{\left(a^{\sqrt{3}-1}\right)}^{\sqrt{3}+1}}$$\hspace{0.17em}=\frac{a^{\sqrt{5}+\text{\hspace{0.17em}}2+\text{\hspace{0.17em}\hspace{0.17em}}4-\sqrt{5}}\text{}}{a^{(\sqrt{3}-1).(\sqrt{3}+1)}}$$=\frac{a^6}{a^2}=a^4$

Ví dụ. So sánh các số ${\left(\frac{2}{3}\right)}^{\sqrt{3}+\text{\hspace{0.17em}}1}$ và ${\left(\frac{2}{3}\right)}^2$.

Lời giải:

Ta có: $\sqrt{3}+1>2$ và $0<\frac{2}{3}<1$

Suy ra: ${\left(\frac{2}{3}\right)}^{\sqrt{3}+\text{\hspace{0.17em}}1}$<${\left(\frac{2}{3}\right)}^2$.

3. Khái niệm hàm số lũy thừa

– Hàm số $y=x^{\alpha }$, với $\alpha \in ℝ$, được gọi là hàm số lũy thừa.

Ví dụ. Các hàm số $y=x^{\sqrt{3}+\text{}1};$ $y=\frac{1}{x^2};y=x^5;$ $\hspace{0.17em}y=x^{\pi -3}$ là những hàm số lũy thừa.

– Chú ý:

Tập xác định của hàm số lũy thừa $y=x^{\alpha }$ tùy thuộc vào giá trị của α. Cụ thể:

+ Với α nguyên dương, tập xác định là R.

+ Với α nguyên âm hoặc bằng 0; tập xác định là R\{0}.

+ Với α không nguyên, tập xác định là $(0;+\infty )$.

4. Đạo hàm của hàm số lũy thừa

– Hàm số lũy thừa $y=x^{\alpha }(\alpha \in ℝ)$ có đạo hàm với mọi x > 0 và $\left(x^{\alpha }\right)\text{'}=\alpha .x^{\alpha -1}$.

– Ví dụ.

a) ${\left(x^{\frac{2}{5}}\right)}^{\text{'}}=\frac{2}{5}.x^{\frac{-3}{5}}$

b) ${\left(x^{\sqrt{7}}\right)}^{\text{'}}=\sqrt{7}.x^{\sqrt{7}-1}$.

– Chú ý: Công thức tính đạo hàm của hàm hợp đối với hàm số lũy thừa có dạng:

$\left(u^{\alpha }\right)\text{'}=\alpha .u^{\alpha -1}.u\text{'}$

– Ví dụ. Tính đạo hàm của hàm số $y={(2x{}_2+3x-2)}^{\frac{1}{3}}$.

Lời giải:

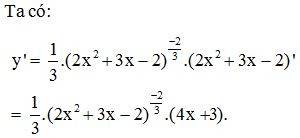
5. Khảo sát hàm số lũy thừa y = x^α

Tập xác định của hàm số lũy thừa $y=x^{\alpha }$ luôn chứa khoảng $(0;+\infty )$ với $\alpha \in R$. Trong trường hợp tổng quát, ta khảo sát hàm số $y=x^{\alpha }$ trên khoảng này (gọi là tập khảo sát).

$y=x^{\alpha };\alpha >\text{\hspace{0.17em}\hspace{0.17em}}0$	$y=x^{\alpha };\alpha <\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}0$
1. Tập khảo sát: $(0;+\text{\hspace{0.17em}}\infty )$ 2. Sự biến thiên $y\text{'}=\alpha .x^{\alpha -1}>0;$$\hspace{0.17em}\forall x>0$ Giới hạn đặc biệt: $$\begin{gathered} \underset{x\to 0^{+}}{\lim }{x}^{\alpha }=0; \\ \underset{x\to +\infty }{\lim }{x}^{\alpha }=+\infty \end{gathered}$$ Tiệm cận: Không có 3. Bảng biến thiên 4. Đồ thị (với α > 0)	1. Tập khảo sát: $(0;+\text{\hspace{0.17em}}\infty )$ 2. Sự biến thiên $y\text{'}=\alpha .x^{\alpha -1}<0;$$\forall x>0$ Giới hạn đặc biệt: $$\begin{gathered} \underset{x\to 0^{+}}{\lim }{x}^{\alpha }=+\infty ; \\ \underset{x\to +\infty }{\lim }{x}^{\alpha }=0 \end{gathered}$$ Tiệm cận: Trục Ox là tiệm cận ngang. Trục Oy là tiệm cận đứng của đồ thị. 3. Bảng biến thiên. 4. Đồ thị (với α < 0)

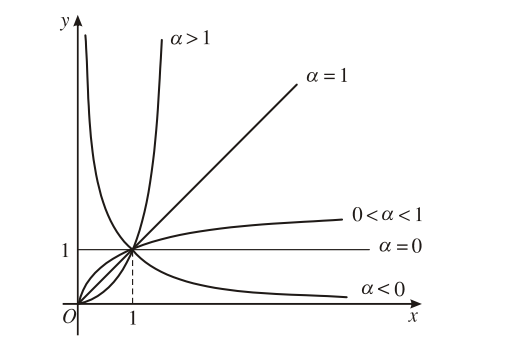
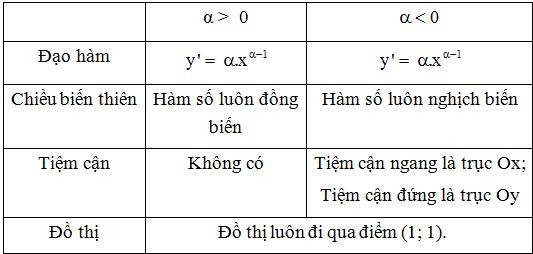
Đồ thị của hàm số lũy thừa y = x^α luôn đi qua điểm (1; 1).

– Chú ý: Khi khảo sát hàm số lũy thừa với số mũ cụ thể, ta phải xét hàm số đó trên toàn bộ tập xác định của nó.

Ví dụ. Khảo sát sự biến thiên và vẽ đồ thị của hàm số $y=x^{\frac{-2}{5}}$.

Lời giải:
1. Tập xác định: $D=\left(0;+\text{}\infty \right)$

2. Sự biến thiên.

Chiều biến thiên $y\text{'}=\frac{-2}{5}{x}^{\frac{-7}{5}}$

Ta có: y’ < 0 trên khoảng $D=\left(0;+\infty \right)$ nên hàm số đã cho nghịch biến.

Tiệm cận: $\underset{x\to 0^{+}}{\lim }y=+\infty ;$$\underset{x\to +\text{\hspace{0.17em}\hspace{0.17em}}\infty }{\lim }y=0$

Đồ thị có tiệm cận ngang là trục hoành và có tiệm cận đứng là trục tung.

Bảng biến thiên

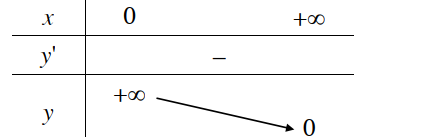
3. Đồ thị

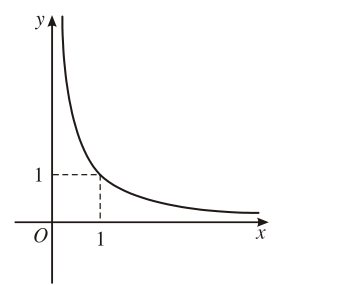
Bảng tóm tắt các tính chất của hàm số lũy thừa $y=x^{\alpha }$ trên khoảng $(0;+\text{\hspace{0.17em}}\infty )$.

6. Khái niệm về lôgarit

6.1 Định nghĩa

Cho hai số dương a; b với a ≠ 1 . Số α thỏa mãn đẳng thức a^α = b được gọi là logarit cơ số a của b và kí hiệu là log_ab.

$\alpha ={\log }_{a}b$$\hspace{0.17em}\iff a^{\alpha }=b$

Ví dụ.

a) log₃ 27 = 3 vì 3³ = 27.

b) ${\log }_4\left(\frac{1}{16}\right)=-2$ vì $4^{-2}=\frac{1}{16}$.

– Chú ý: Không có logarit của số âm và số 0.

6.2 Tính chất

Cho hai số dương a và b; a ≠ 1. Ta có các tính chất sau đây:

log_a1 = 0; log_aa = 1

$a^{{\log }_{a}b}=b;\log {}_a\left(a^{\alpha }\right)=\alpha$

Ví dụ.

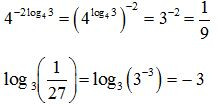
7. Quy tắc tính logarit

7.1 Logarit của một tích

– Định lí 1. Cho ba số dương a; b₁ ;b₂ với a ≠ 1. Ta có:

${\log }_a(b_1.b{}_2)={\log }_a{b}_1+{\log }_{a}b{}_2$

Logarit của một tích bằng tổng các logarit.

Ví dụ.

$$\begin{gathered} {\log }_{2}12+\text{\hspace{0.17em}}{\log }_2\frac{1}{3} \\ ={\log }_2\left(12.\frac{1}{3}\right) \\ ={\log }_{2}4=2 \end{gathered}$$

– Chú ý:

Định lí 1 có thể mở rộng cho tích n số dương:

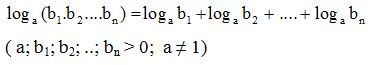
7.2 Logarit của một thương

– Định lí 2. Cho ba số dương a; b₁ ;b₂ với a ≠ 1. Ta có:

${\log }_a\frac{b_1}{b_2}={\log }_a{b}_1-{\log }_{a}b{}_2$

Logarit của một thương bằng hiệu các logarit.

Đặc biệt: ${\log }_a\frac{1}{b}=-{\log }_{a}b$ ( a > 0; b > 0; a ≠ 1)

– Ví dụ 4.

$$\begin{gathered} \log {}_{5}75-{\log }_{5}3 \\ ={\log }_5\frac{75}{3} \\ ={\log }_{5}25=2 \end{gathered}$$

7.3 Logarit của một lũy thừa.

– Định lí 3. Cho hai số dương a; b và a ≠ 1 . Với mọi số α, ta có:

${\log }_a{b}^{\alpha }=\alpha {\log }_{a}b$

Logarit của một lũy thừa bằng tích của số mũ với logarit của cơ số.

– Đặc biệt: ${\log }_a\sqrt[n]{b}=\frac{1}{n}{\log }_{a}b$

– Ví dụ 5.

$\begin{array}{l}\log {}_7{3}^6=6{\log }_{7}3\\ {\log }_3\sqrt[5]{4}=\frac{1}{5}{\log }_{3}4\end{array}$

8. Công thức đổi cơ số của logarit.

– Định lí 4. Cho ba số dương a; b; c với a ≠ 1; c ≠ 1, ta có:

${\log }_{a}b=\frac{{\log }_{c}b}{{\log }_{c}a}$

– Đặc biệt:

$\begin{array}{l}{\log }_{a}b=\frac{1}{{\log }_{b}a}(b\ne 1)\\ {\log }_{a^{\alpha }}b=\frac{1}{\alpha }{\log }_{a}b(\alpha \ne 0)\end{array}$

Ví dụ. Tính giá trị các biểu thức sau:

a) $5^{{\log }_{\frac{1}{125}}8}$

b) ${\log }_{2}3.{\log }_{3}4.\mathrm{....}{\log }_{7}8$

Lời giải:

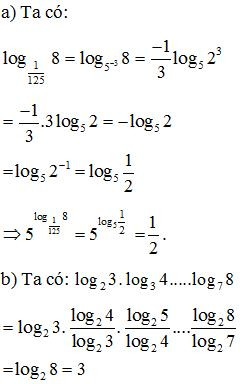
9. Logarit thập phân. Logarit tự nhiên.

9.1 Logarit thập phân

Logarit thập phân là logarit cơ số 10.

log₁₀b thường được viết là logb hoặc lgb.

9.2 Logarit tự nhiên

– Logarit tự nhiên là logarit cơ số e.

log_eb được viết là lnb.

10. Hàm số mũ

10.1 Định nghĩa.

Cho số thực dương a khác 1.

Hàm số y = a^x được gọi là hàm số mũ cơ số a.

Ví dụ. Các hàm số y = 2^x; $y={\left(\frac{1}{2}\right)}^x;$$\hspace{0.17em}y={\left(\sqrt{3}\right)}^x$ là các hàm số mũ.

10.2 Đạo hàm của hàm số mũ

Ta thừa nhận công thức: $\underset{t\to 0}{\lim }\frac{e^t-1}{t}=1$

– Định lí 1: Hàm số y = e^x có đạo hàm tại mọi x và (e^x)’ = e^x.

– Chú ý: Công thức đạo hàm của hàm hợp đối với hàm số e^u ( với u = u(x))

là (e^u)’ = u’. e^u.

– Định lí 2: Hàm số y = a^x ( a > 0; a ≠ 1) có đạo hàm tại mọi x và: (a^x)’ = a^x. ln a

– Chú ý: Đối với hàm hợp y = a^u(x) ta có: (a^u)’ = a^u. lnu . u’

Ví dụ. Hàm số $y=2^{-x^2+\text{\hspace{0.17em}}2x-10}$ có đạo hàm là:

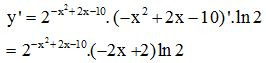
10.3 Khảo sát hàm số mũ y = a^x (a > 0 và a ≠ 1).

y = ax ; a > 1	y = ax ; 0 < a < 1
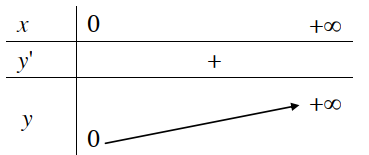
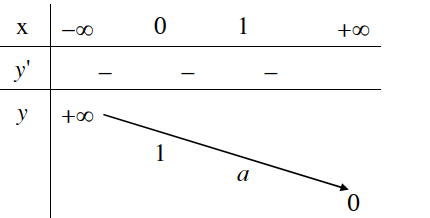
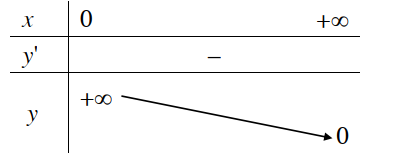
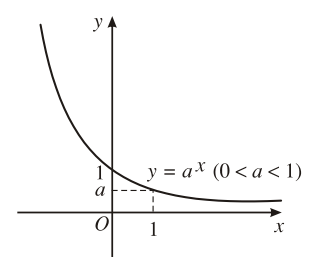
1. Tập xác định: R 2. Sự biến thiên y’ = ax.ln a > 0 với mọi x Giới hạn đặc biệt: $$\begin{gathered} \underset{x\to -\infty }{\lim }{a}^x=0; \\ \underset{x\to +\infty }{\lim }{a}^x=+\infty \end{gathered}$$ Tiệm cận: Trục Ox là tiệm cận ngang. 3. Bảng biến thiên: 4. Đồ thị	1. Tập xác định: R 2. Sự biến thiên y’ = ax.ln a < 0 với mọi x Giới hạn đặc biệt: $$\begin{gathered} \underset{x\to -\infty }{\lim }{a}^x=+\infty ; \\ \underset{x\to +\infty }{\lim }{a}^x=0 \end{gathered}$$ Tiệm cận: Trục Ox là tiệm cận ngang. 3. Bảng biến thiên: 4. Đồ thị

Bảng tóm tắt các tính chất của hàm số mũ y = a^x ( a > 0; a ≠ 1).

Tập xác định	$\left(-\infty ;+\infty \right)$
Đạo hàm	y’ = ax. lna
Chiều biến thiên	a > 1: Hàm số luôn đồng biến. 0 < a < 1: Hàm số luôn nghịch biến
Tiệm cận	Trục Ox là tiệm cận ngang
Đồ thị	Đi qua các điểm (0; 1) và (1; a), nằm phía trên trục hoành (y = ax > 0 $\forall x\in ℝ$).

11. Hàm số logarit

11.1 Định nghĩa.

Cho số thực dương a khác 1.

Hàm số y = log_ax được gọi là hàm số logarit cơ số a.

Ví dụ. Các hàm số y = log₅ x; $y={\log }_{\frac{2}{3}}x;$$y={\log }_{\sqrt{3}}x$; y = ln x là các hàm số logarit với cơ số lần lượt là $5;\frac{2}{3};\sqrt{3}$ và e.

11.2 Đạo hàm của hàm số logarit

– Định lí 3. Hàm số y = log_a x (a > 0; a ≠ 1) có đạo hàm tại mọi x > 0 và $\left({\log }_{a}x\right)\text{'}=\frac{1}{x\ln a}$

– Đặc biệt: $\left(\ln x\right)\text{'}=\frac{1}{x}$

– Chú ý:

Đối với hàm hợp y = log_au(x); ta có: $\left({\log }_{a}u\right)\text{'}=\frac{u\text{'}}{u\ln a}$

– Ví dụ. Hàm số y = log₄ (x² + 2x – 7) có đạo hàm là:

$$\begin{gathered} \left({\log }_4\right(x^2+\text{\hspace{0.17em}\hspace{0.17em}}2x-7\left)\right)\text{'} \\ =\frac{(x^2+2x-7)\text{'}}{(x^2+2x-7)\ln 4} \\ =\frac{2x+2}{(x^2+2x-7)\ln 4} \end{gathered}$$

11.3 Khảo sát hàm số logarit y = log_a x ( a > 0; a ≠ 1).

y = loga x ; a > 1

y = logax ; 0 < a < 1

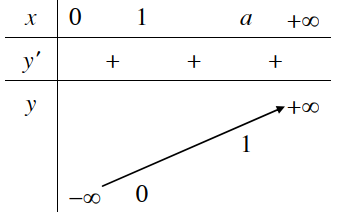
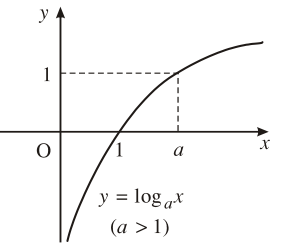
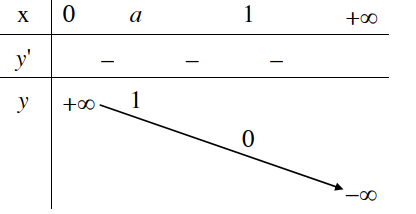
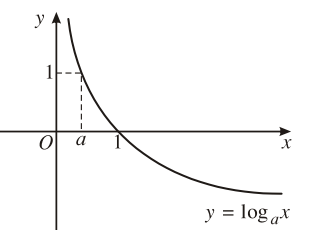
1. Tập xác định: $(0;+\text{\hspace{0.17em}}\infty )$ 2. Sự biến thiên $y\text{'}=\frac{1}{x\ln a}>\text{\hspace{0.17em}\hspace{0.17em}}0;$$\hspace{0.17em}\forall x>0$ Giới hạn đặc biệt: $\begin{array}{l}\underset{x\to 0^{+}}{\lim }{\log }_{a}x=-\infty ;\\ \underset{x\to +\infty }{\lim }{\log }_{a}x=+\infty .\end{array}$ Tiệm cận: Trục Oy là tiệm cận đứng. 3. Bảng biến thiên 4. Đồ thị

1. Tập xác định: $(0;+\text{\hspace{0.17em}}\infty )$ 2. Sự biến thiên $y\text{'}=\frac{1}{x\ln a}<\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}0;$$\hspace{0.17em}\forall x>0$ Giới hạn đặc biệt: $\begin{array}{l}\underset{x\to 0^{+}}{\lim }{\log }_{a}x=+\infty ;\\ \underset{x\to +\infty }{\lim }{\log }_{a}x=-\infty .\end{array}$ Tiệm cận: Trục Oy là tiệm cận đứng. 3. Bảng biến thiên 4. Đồ thị

Bảng tóm tắt các tính chất của hàm số y = log_ax (a > 0; a ≠ 1 ).

Tập xác định	$\left(0;+\infty \right)$
Đạo hàm	$y\text{'}=\frac{1}{x\ln a}$
Chiều biến thiên	a > 1: hàm số luôn đồng biến 0 < a < 1: hàm số luôn nghịch biến
Tiệm cận	Trục Oy là tiệm cận đứng
Đồ thị	Đi qua các điểm (1; 0) và (a; 1); nằm phía bên phải trục tung

Nhận xét:

Đồ thị của các hàm số y = a^x và y = log_a x ( a > 0; a ≠ 1) đối xứng với nhau qua đường thẳng y = x.

Bảng đạo hàm của các hàm số lũy thừa, mũ, logarit.

12. Phương trình mũ

12.1 Phương trình mũ cơ bản

– Phương trình mũ cơ bản có dạng: a^x = b (a > 0; a ≠ 1).

Để giải phương trình trên, ta sử dụng định nghĩa logarit.

Với b > 0 ta có: a^x = b$\iff$x = log_ab.

Với b ≤ 0, phương trình vô nghiệm.

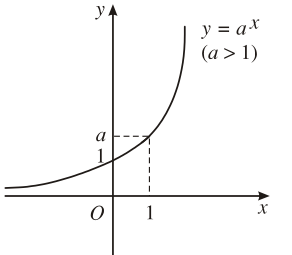
– Minh họa bằng đồ thị

Hoành độ giao điểm của đồ thị hai hàm số y = a^x và y = b là nghiệm của phương trình a^x = b.

Số nghiệm của phương trình là số giao điểm của hai đồ thị.

Rõ ràng, nếu b ≤ 0 thì hai đồ thị không cắt nhau nên phương trình vô nghiệm.

Nếu b > 0 ta có hai đồ thị như hình dưới đây. Trên mỗi hình, hai đồ thị luôn cắt nhau tại một điểm nên phương trình có nghiệm duy nhất.

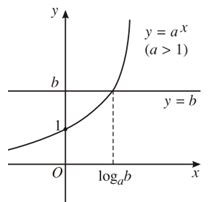
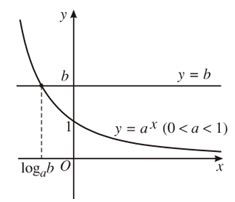
Kết luận:

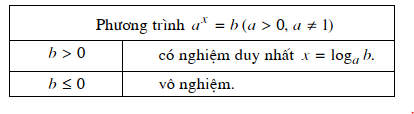
– Ví dụ. Giải phương trình 2^{x + 1} + 2^{x + 2} = 16.

Lời giải:

Ta có: 2^{x + 1} + 2^{x + 2} = 16.

$\iff$2.2^x + 4.2^x = 16

$\iff$6.2^x = 16

$$\begin{gathered} \iff 2^x=\frac{8}{3} \\ \iff x={\log }_2\frac{8}{3} \end{gathered}$$

Vậy $x={\log }_2\frac{8}{3}$.

12.2 Cách giải một số phương trình mũ cơ bản

a) Đưa về cùng cơ số.

– Ví dụ. Giải phương trình $3^{x+\text{\hspace{0.17em}}2}={\left(\frac{1}{3}\right)}^{6-2x}$

Lời giải:

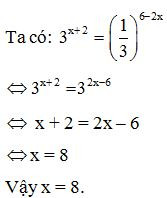
b) Đặt ẩn phụ

– Ví dụ. Giải phương trình 4^x – 5. 2^x + 6 = 0

Lời giải:

Đặt t = 2^x (với t > 0)

Phương trình đã cho trở thành: t² – 5t + 6 = 0

$$\begin{gathered} \iff \left[\begin{array}{c}t=2\\ t=3\end{array}\right. \\ \Rightarrow \left[\begin{array}{c}{2}^x=2\Rightarrow x=1\\ 2^x=3\Rightarrow x={\log }_{2}3\end{array}\right. \end{gathered}$$

Vậy phương trình đã cho có 2 nghiệm là x = 1 và x = log₂3.

c) Logarit hóa.

– Ví dụ. Giải phương trình: $3^x.5^{x^2}=1$

Lời giải:

Lấy logarit cơ số 3 hai vế ta được:

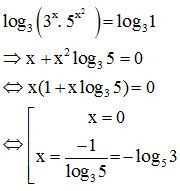
Vậy phương trình đã cho có 2 nghiệm là x = 0 và x = – log₅3.

13. Phương trình logarit

– Phương trình logarit là phương trình có chứa ẩn số trong biểu thức dưới dấu logarit.

– Ví dụ. Các phương trình $\log {}_{2}x=4;$$\hspace{0.17em}{\log }_3^{2}x+\text{\hspace{0.17em}}2{\log }_{4}x=0$… đều là phương trình logarit.

13.1 Phương trình logarit cơ bản

– Phương trình logarit cơ bản có dạng: log_ax = b (a > 0; a ≠ 1).

Theo định nghĩa logarit ta có:

log_ax = b$\iff$x = a^b

– Minh họa bằng đồ thị

Vẽ đồ thị hàm số y = log_a x và đường thẳng b trên cùng một hệ tọa độ.

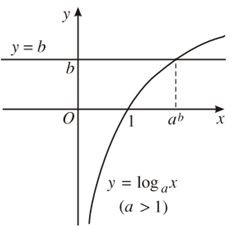
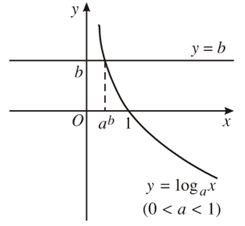
Trong cả hai trường hợp, ta đều thấy đồ thị của các hàm số y = log_ax và đường thẳng y = b luôn cắt nhau tại một điểm với mọi b$\in R$.

Kết luận: Phương trình log_ax = b (a > 0; a ≠ 1) luôn có nghiệm duy nhất x = a^b với mọi b.

13.2 Cách giải một số phương trình logarit đơn giản.

a) Đưa về cùng cơ số

Ví dụ. Giải phương trình log₃x + log₉x = 6.

Lời giải:

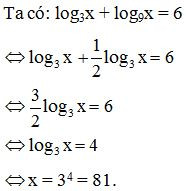
Vậy nghiệm của phương trình đã cho là x = 81.

b) Đặt ẩn phụ

– Ví dụ. Giải phương trình ${\log }_5^{2}x+\text{}3{\log }_5^{}x=0$

Lời giải:

Đặt t = log₅x, phương trình đã cho trở thành:

t² + 3t = 0 nên t = 0 hoặc t = –3.

Với t = 0 thì log₅x = 0 nên x = 1.

Với t = –3 thì log₅x = –3 nên x = 5^–3.

Vậy phương trình đã cho có 2 nghiệm là x = 1 và x = 5^–3.

c) Mũ hóa

– Ví dụ. Giải phương trình: log₃(90 – 3^x) = x + 2

Lời giải:

Điều kiện của phương trình là 90 – 3^x > 0.

Phương trình đã cho tương đương với:

90 – 3^x = 3^{x + 2} hay 90 – 3^x = 9.3^x

$\iff$10.3^x = 90

$\iff$3^x = 9 nên x = 2 (thỏa mãn điều kiện)

Vậy nghiệm của phương trình đã cho là x = 2.

14. Bất phương trình mũ.

14.1 Bất phương trình mũ cơ bản

Bất phương trình mũ cơ bản có dạng a^x > b ( hoặc a^x < b; $a^x\ge b;a^x\le b$) với a > 0 và a ≠ 1.

Ta xét bất phương trình a^x > b

+ Nếu b ≤ 0 tập nghiệm của bất phương trình là R vì a^x > 0$\ge b;\forall x\in ℝ$

+ Nếu b > 0 thì tập nghiệm của bất phương trình tương đương $a^x>a^{{\log }_{a}b}$.

Với a > 1, tập nghiệm của bất phương trình là x > log_ab.

Với 0 < a < 1, tập nghiệm của bất phương trình là x < log_ab.

– Ví dụ.

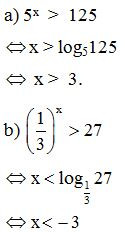
Kết luận. Tập nghiệm của bất phương trình a^x > b được cho trong bảng sau:

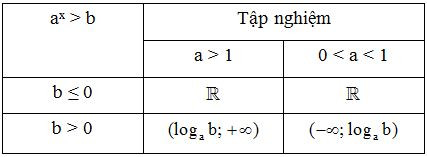
14.2 Bất phương trình mũ đơn giản

– Ví dụ. Giải bất phương trình 3^{x + 2} < 27.

Lời giải:

Ta có: 27 = 3³

Vì cơ số 3 > 1 nên x + 2 < 3

$\iff$x < 1.

Vậy tập nghiệm của bất phương trình đã cho là x < 1.

15. Bất phương trình logarit

15.1 Bất phương trình logarit cơ bản

Bất phương trình logarit cơ bản có dạng log_a x > b ( hoặc log_ax < 0; ${\log }_{a}x\le 0;$$\hspace{0.17em}{\log }_{a}x\ge 0$) với a > 0; a ≠ 1.

Xét bất phương trình log_ax > b

+ Trường hợp a > 1 ta có: log_ax > b$\iff$x > a^b.

+ Trường hợp 0 < a < 1 ta có: log_ax > b$\iff$0 < x < a^b.

– Ví dụ.

a) log₂x > 7$\iff$x > 2⁷.

b) ${\log }_{\frac{2}{5}}x<3$$\hspace{0.17em}\iff x\text{\hspace{0.17em}\hspace{0.17em}}>{\left(\frac{2}{5}\right)}^3$

Kết luận: Nghiệm của bất phương trình log_ax > b được cho trong bảng sau:

logax > b	a > 1	0 < a < 1
Nghiệm	x > ab	0 < x < ab

15.2 Bất phương trình logarit đơn giản

– Ví dụ. Giải bất phương trình ${\log }_3(x^2+\text{}2x)>\text{\hspace{0.17em}\hspace{0.17em}}{\log }_3(x+2)$.

Lời giải:

Điều kiện của bất phương trình:

$$\begin{gathered} \left\{\begin{array}{c}{x}^2+2x\text{\hspace{0.17em}\hspace{0.17em}}>0\\ x+\text{\hspace{0.17em}\hspace{0.17em}}2>\text{\hspace{0.17em}\hspace{0.17em}}0\end{array}\right. \\ \iff \left[\begin{array}{c}\left[\begin{array}{c}x>\text{\hspace{0.17em}}0\\ x<-2\end{array}\right.\\ x>\text{\hspace{0.17em}}-2\end{array}\right. \\ \iff x>0 \end{gathered}$$

Ta có: ${\log }_3(x^2+\text{}2x)>\text{\hspace{0.17em}\hspace{0.17em}}{\log }_3(x+2)$

Vì cơ số 3 > 1 nên: x² + 2x > x + 2

$\iff$x² + x – 2 > 0$\iff \left[\begin{array}{c}x>\text{\hspace{0.17em}\hspace{0.17em}}1\\ x\text{\hspace{0.17em}}<-2\end{array}\right.$

Kết hợp điều kiện, vậy x > 1.

B. Bài tập tự luyện

Bài 1. Tính

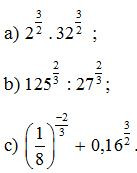
Lời giải:

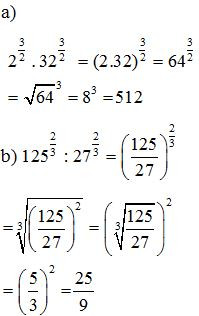
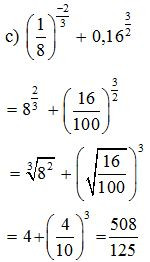
Bài 2. Cho a, x là những số thực dương. Viết các biểu thức sau dưới dạng lũy thừa với số mũ hữu tỉ:

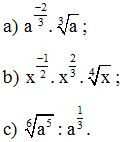
Lời giải:

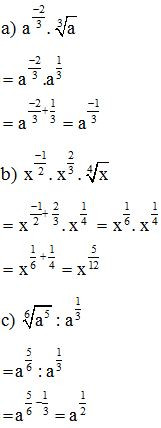
Bài 3. So sánh các số sau:

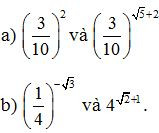
Lời giải:

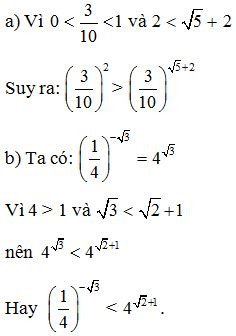
Bài 4. Tìm điều kiện xác định của các hàm số

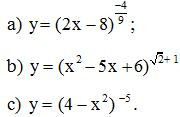
Lời giải:

a) Vì $\frac{-4}{9}$ là số hữu tỉ nên điều kiện của hàm số là:

2x – 8 > 0 hay x > 4.

b) Vì là số vô tỉ nên điều kiện của hàm số là:

x² – 5x + 6 > 0$\iff \left[\begin{array}{c}x>3\\ x<2\end{array}\right.$

c) Vì – 5 là số nguyên âm nên điều kiện của hàm số là 4 – x² > 0 hay – 2 < x < 2.

Bài 5. Tính đạo hàm của các hàm số

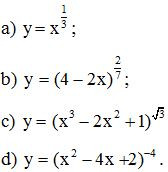
Lời giải:

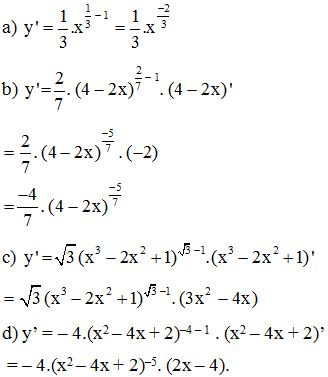
Bài 6. Hãy so sánh các cặp số sau :

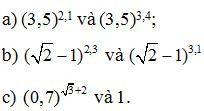
Lời giải:

Bài 7. Tìm điều điện của a để các biểu thức sau có nghĩa.

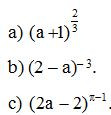
Lời giải:

a) Ta có: $\frac{2}{3}$ là số hữu tỉ nên để biểu thức đã cho có nghĩa thì a + 1 > 0 hay a > –1.

b) Vì – 3 là số nguyên âm nên để biểu thức đã cho có nghĩa thì 2 – a ≠ 0 hay a ≠ 2.

c) Vì $\mathrm{\pi }-1$ là số vô tỉ nên để biểu thức đã cho có nghĩa thì 2a – 2 > 0 hay a > 1.

Bài 8. Tính:

Lời giải:

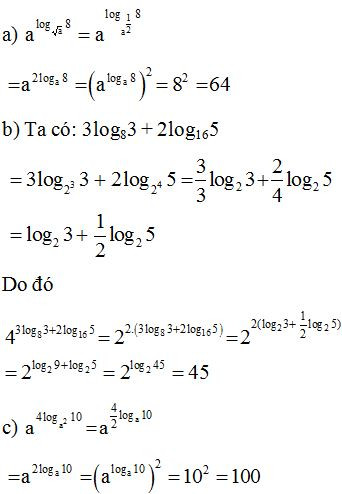
Bài 9. Tính

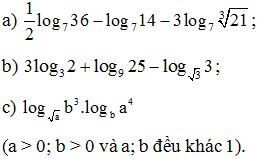
Lời giải:

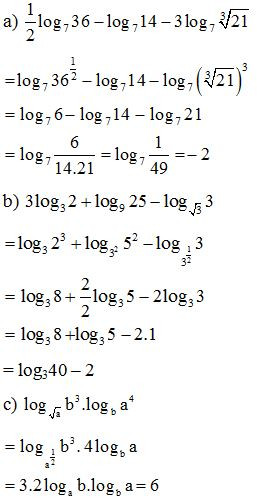
Bài 10. Biết log₇2 = m . Tính giá trị của biểu thức log₄₉ 28 theo m?

Lời giải:

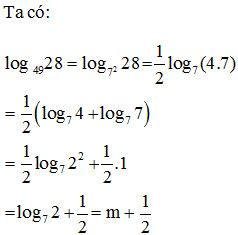
Bài 11. Tính đạo hàm của các hàm số

Lời giải:

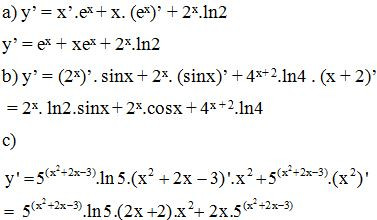
Bài 12. Tìm điều kiện xác định của các hàm số sau:

a) y = log₄ (x² – 4);

b) y = log₃ (2x – x²);

c) $y={\log }_{\sqrt{3}}\sqrt{x^2-x}$.

Lời giải:

a) Điều kiện: x² – 4 > 0$\iff \left[\begin{array}{c}x>\text{\hspace{0.17em}\hspace{0.17em}}2\\ x<-2\end{array}\right.$

b) Điều kiện: 2x – x² > 0 hay 0 < x < 2 .

c) Điều kiện: x² – x > 0$\iff \left[\begin{array}{c}x>\text{\hspace{0.17em}\hspace{0.17em}}1\\ x<0\end{array}\right.$

Bài 13. Tính đạo hàm của các hàm số sau:

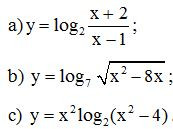
Lời giải:

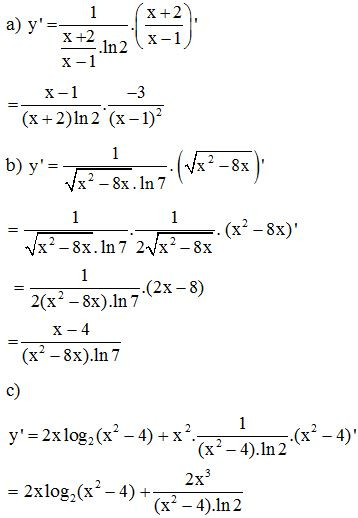
Bài 14. Giải phương trình mũ.

a) $3^{x^2+\text{\hspace{0.17em}}2x-1}=9$;

b) 2^{x+ 1} + 2^{x+ 2} + 2^{x+ 3} = 56;

c) 25^x – 5^{x+ 1} + 6 = 0.

Lời giải:

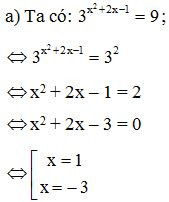
Vậy phương trình đã cho có nghiệm là x = 1 và x = –3.

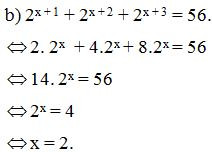
Vậy nghiệm của phương trình đã cho là x = 2.

c) 25^x – 5^{x+ 1} + 6 = 0

$\iff$5^2x – 5. 5^x + 6 = 0

Đặt t = 5^x ( t > 0) phương trình trên trở thành: t² – 5t + 6 = 0

$$\begin{gathered} \iff \left[\begin{array}{c}t=2\\ t=3\end{array}\right. \\ \Rightarrow \left[\begin{array}{c}{5}^x=2\\ 5^x=3\end{array}\right. \\ \iff \left[\begin{array}{c}x={\log }_{5}2\\ x={\log }_{5}3\end{array}\right. \end{gathered}$$

Vậy nghiệm của phương trình là $x={\log }_{5}2;x={\log }_{5}3.$

Bài 15. Giải phương trình logarit

a) log₇(10 – x) = log₇(x – 4);

b) log₃(x + 2) – log₃(4 – x) = 2;

c) ${\log }_2^{2}x-7{\log }_{2}x+\text{\hspace{0.17em}}6=0$;

d) log₃(3^x – 12) = 2x + 2.

Lời giải:

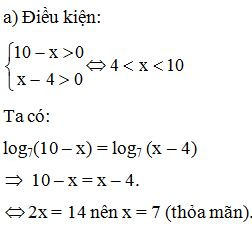
Vậy phương trình đã cho có nghiệm duy nhất là x = 7.

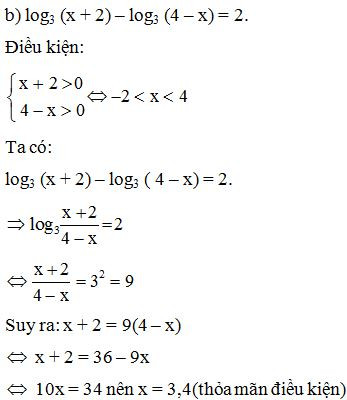
Vậy nghiệm của phương trình đã cho là x = 3,4.

c) ${\log }_2^{2}x-7{\log }_{2}x+\text{\hspace{0.17em}}6=0$(điều kiện x > 0).

Đặt t = log₂x, phương trình đã cho trở thành: t² – 7t + 6 = 0

$$\begin{gathered} \iff \left[\begin{array}{c}t=1\\ t=6\end{array}\right. \\ \Rightarrow \left[\begin{array}{c}{\log }_{2}x=1\\ {\log }_{2}x=6\end{array}\right. \\ \iff \left[\begin{array}{c}x=2\\ x=64\end{array}\right. \end{gathered}$$

Vậy nghiệm của phương trình đã cho là x = 2 và x = 64.

d) log₃(3^x – 12) = 2x + 2

Điều kiện: 3^x – 12 > 0

Phương trình đã cho tương đương:

3^x – 12 = 3^{2x + 2} hay 9.3^2x – 3^x + 12 = 0 (*)

Đặt t = 3^x ( t > 0), phương trình (*) trở thành: 9t² – t + 12 = 0

Phương trình trên vô nghiệm nên phương trình đã cho vô nghiệm.

Bài 16. Giải các bất phương trình

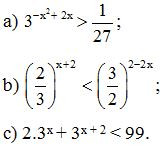
Lời giải:

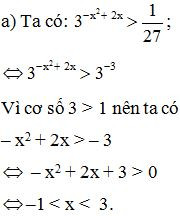
Vậy tập nghiệm của bất phương trình là – 1 < x < 3.

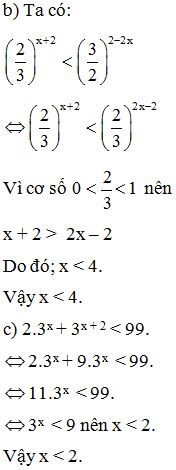
Bài 17. Giải các bất phương trình logarit:

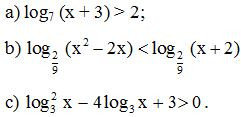
Lời giải:

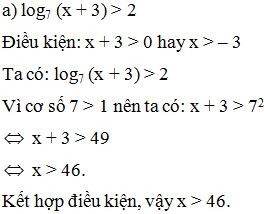
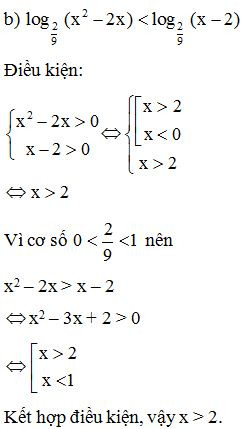
Trắc nghiệm Toán 12 Bài: Ôn tập Chương 2

Câu 1. Cho hàm số $y=e^x+e^{-x}$. Tính $y\text{'}\text{'}\left(1\right)$

A. $e+\frac{1}{e}$

B. $e-\frac{1}{e}$

C. $-e+\frac{1}{e}$

D. $-e-\frac{1}{e}$

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có: $y\text{'}=e^x-e^{-x}$

$\Rightarrow y\text{'}\text{'}=e^x+e^{-x}$

$\Rightarrow y\text{'}\text{'}\left(1\right)=e+\frac{1}{e}$

Câu 2. Hàm số $y={\left(x^2-16\right)}^{-5}-\ln \left(24-5x-x^2\right)$ có tập xác định là:

A. $\left(-8;-4\right)\cup \left(3;+\infty \right)$

B. $\left(-\infty ;-4\right)\cup \left(3;+\infty \right)$

C. $\left(-8;3\right)\backslash \left\{-4\right\}$

D. $\left(-4;3\right)$

Hiển thị đáp án

Đáp án: C

Giải thích:

Điều kiện xác định của hàm số $y={\left(x^2-16\right)}^{-5}-\ln \left(24-5x-x^2\right)$ là:

$\left\{\begin{array}{c}{x}^2-16\ne 0\\ 24-5x-x^2>0\end{array}\right.$

$\iff \left\{\begin{array}{c}x\ne \pm 4\\ -8<x<3\end{array}\right.$

Vậy tập xác định là: $D=\left(-8;3\right)\backslash \left\{-4\right\}$

Câu 3. Đạo hàm của hàm số $y={\log }_3\left(4x+1\right)$ là:

A. $y\text{'}=\frac{1}{\left(4x+1\right)\ln 3}$

B. $y\text{'}=\frac{4}{\left(4x+1\right)\ln 3}$

C. $y\text{'}=\frac{\ln 3}{4x+1}$

D. $y\text{'}=\frac{4\ln 3}{4x+1}$

Hiển thị đáp án

Đáp án: B

Giải thích:

Với $x>-\frac{1}{4}$

Áp dụng công thức $\left({\log }_{a}u\right)\text{'}=\frac{u\text{'}}{u\ln a}$ ta có: $y\text{'}=\frac{4}{\left(4x+1\right)\ln 3}$

Câu 4. Tìm tập nghiệm S của hệ phương trình $\left\{\begin{array}{l}{3}^x={27.3}^y\\ \log \left(x+2y\right)=\log 5+\log 3\end{array}\right.$

A. $S=\left\{\left(7;4\right)\right\}.$

B. $S=\left\{\left(4;7\right)\right\}.$

C. $S=\left\{\left(6;3\right)\right\}.$

D. $S=\left\{\left(9;6\right)\right\}.$

Hiển thị đáp án

Đáp án: A

Giải thích:

Điều kiện: $x+2y>0.$

Hệ phương trình $\iff \left\{\begin{array}{l}{3}^x=3^3{.3}^y\\ \log \left(x+2y\right)=\log 15\end{array}\right.$

$\iff \left\{\begin{array}{l}x=y+3\\ x+2y=15\end{array}\right.$

$\iff \left\{\begin{array}{l}x=7\\ y=4\end{array}\right.$

Cách 2. Dùng CASIO thử từng đáp án.

Câu 5. Tìm tất cả các cặp số $\left(x;y\right)$ thỏa mãn $\frac{4^x}{2^y}=2$ và $\log \left(2x+2y\right)=1$.

A. $\left(x;y\right)=\left(4;1\right).$

B. $\left(x;y\right)=\left(2;3\right).$

C. $\left(x;y\right)=\left(3;2\right).$

D. $\left(x;y\right)=\left(5;9\right).$

Hiển thị đáp án

Đáp án: B

Giải thích:

Điều kiện: $x+y>0$.

$\frac{4^x}{2^y}=2\iff 2^{2x-y}=2$

$\iff 2x-y=1. \left(1\right)$

$\log \left(2x+2y\right)=1$

$\iff 2x+2y=10. \left(2\right)$

Từ (1) và (2), ta có hệ $\left\{\begin{array}{l}2x-y=1\\ 2x+2y=10\end{array}\right.$

$\iff \left\{\begin{array}{l}x=2\\ y=3\end{array}\right..$

Câu 6. Hàm số nào trong hàm số sau đây có đồ thị phù hợp với hình vẽ bên?

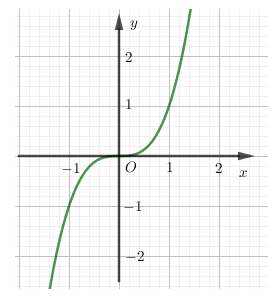
A. $y=x^3$

B. $y=x^{-4}$

C. $y=x^{\frac{1}{5}}$

D. $y=\sqrt{x}$

Hiển thị đáp án

Đáp án: A

Giải thích:

Đồ thị của hình vẽ là đồ thị hàm bậc ba y = x³

Câu 7. Cho ${\log }_{2}3=a;{\log }_{2}7=b$. Tính ${\log }_{2}2016$ theo a và b

A. $5+2a+b$

B. $5+3a+2b$

C. $2+2a+3b$

D. $2+3a+2b$

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có: ${\log }_{2}2016={\log }_2\left(2^5{3}^{2}7\right)$

$={\log }_2{2}^5+{\log }_2{3}^2+{\log }_{2}7$

$=5+2a+b$

Câu 8. Cho a, b > 0. Khẳng định nào sau đây đúng?

A. $a^{\ln b}=b^{\ln a}$

B. ${\ln }^2\left(ab\right)=\ln a^2+\ln b^2$

C. $\ln \left(\frac{a}{b}\right)=\frac{\ln a}{\ln b}$

D. $\ln \sqrt{ab}=\frac{1}{2}\left(\ln \sqrt{a}+\ln \sqrt{b}\right)$

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có: $\ln a.\ln b=\ln b.\ln a$

$\iff \ln \left(b^{\ln a}\right)=\ln \left(a^{\ln b}\right)$

$\iff b^{\ln a}=a^{\ln b}$

Câu 9. Tính giá trị của biểu thức $P=\ln \left(\tan 1^0\right)+\ln \left(\tan 2^0\right)+\mathrm{..}+\ln \left(\tan {89}^0\right)$

A. 1

B. $\frac{1}{2}$

C. 0

D. 2

Hiển thị đáp án

Đáp án: C

Giải thích:

Câu 10. Cho hệ phương trình $\left\{\begin{array}{l}{\left(\frac{2}{3}\right)}^{2x-y}+6{\left(\frac{2}{3}\right)}^{\frac{2x-y}{2}}-7=0\\ 3^{{\log }_9\left(x-y\right)}=1\end{array}\right.$. Chọn khẳng định đúng?

A. Điều kiện xác định của hệ phương trình là $x>y>0$

B. Hệ phương trình đã cho có hai nghiệm $\left(x;y\right)$

C. Hệ phương trình đã cho có một nghiệm duy nhất $\left(x;y\right)=\left(-1;-2\right)$

D. Hệ phương trình đã cho vô nghiệm.

Hiển thị đáp án

Đáp án: C

Giải thích:

Điều kiện: $x-y>0\iff x>y$. Do đó A sai.

Xét phương trình thứ nhất của hệ: ${\left(\frac{2}{3}\right)}^{2x-y}+6{\left(\frac{2}{3}\right)}^{\frac{2x-y}{2}}-7=0$.

Đặt $t={\left(\frac{2}{3}\right)}^{\frac{2x-y}{2}}>0$, phương trình trở thành

$t^2+6t-7=0$

$\iff \left[\begin{array}{l}t=1\left(tm\right)\\ t=-7\left(loại\right)\end{array}\right.$

$\stackrel{}{\to }{\left(\frac{2}{3}\right)}^{\frac{2x-y}{2}}=1$

$\iff \frac{2x-y}{2}=0.$

Phương tình thứ hai của hệ:

$3^{{\log }_9\left(x-y\right)}=1$

$\iff 3^{{\log }_9\left(x-y\right)}=3^0$

$\iff {\log }_9\left(x-y\right)=0$

$\iff x-y=1.$

Từ đó ta có $\iff \left\{\begin{array}{l}2x-y=0\\ x-y=1\end{array}\right.$

$\iff \left\{\begin{array}{l}x=-1\\ y=-2\end{array}\right.$ thỏa mãn điều kiện.

Vậy hệ phương trình đã cho có một nghiệm duy nhất $\left(x;y\right)=\left(-1;-2\right)$

Xem thêm các bài tổng hợp lý thuyết Toán lớp 12 đầy đủ, chi tiết khác:

Lý thuyết Nguyên hàm

Lý thuyết Tích phân

Lý thuyết Ứng dụng của tích phân trong hình học

Lý thuyết Ôn tập chương 3

Lý thuyết Số phức