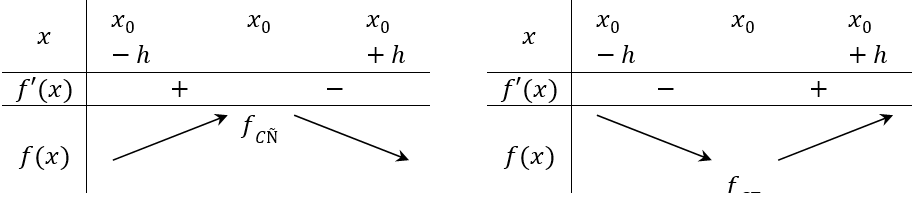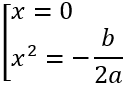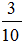Câu hỏi:
12/04/2025 80Tìm m để giá trị nhỏ nhất của hàm số trên đoạn [0;3] bằng 2 .
A. 2
B. 31/27
C. m > 3/4
D. m = 1
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng : D
*Lời giải:
*Phương pháp giải:
- Để xét điểm cực trị hàm số, ta sẽ:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Tínhf'(x). Tìm các điểm tại đó f'(x)bằng 0 hoặc f'(x) không xác định.
Bước 3. Lập bảng biến thiên.
Bước 4. Từ bảng biến thiên suy ra các điểm cực trị.
* Các lý thuyết thêm và các dạng bài toán về cực trị hàm số:
1.Định nghĩa: Cho hàm số y = f(x)xác định và liên tục trên khoảng (a;b) (có thể a là -∞; b là +∞) và điểm x0∈(a;b).
Nếu tồn tại số h > 0 sao cho f(x)< f(x0 ) với mọi x ∈ (x0 - h;x0 + h) và x≠x_0 thì ta nói hàm số f(x) đạt cực đại tại x0.
Nếu tồn tại số h >0 sao cho f(x) >f(x0 ) với mọi x ∈ (x0 - h;x0 + h) và x ≠ x0 thì ta nói hàm số f(x) đạt cực tiểu tại x0.
2.Điều kiện đủ để hàm số có cực trị: Giả sử hàm số y=f(x) liên tục trên
K=(x0 - h;x0 + h)và có đạo hàm trên K hoặc trên K\{x0}, với h >0.
Nếu f'(x)> 0 trên khoảng (x0 - h;x0) và f'(x) <0 trên (x0;x0 + h) thì x0 là một điểm cực đại của hàm số f(x).
Nếu f'(x) < 0 trên khoảng (x0 - h;x0) và f'(x) >0 trên (x0;x0+ h) thì x0 là một điểm cực tiểu của hàm số f(x).
Minh họa bằng bảng biến thiến
Chú ý.
Nếu hàm sốy=f(x) đạt cực đại (cực tiểu) tại x0 thì x0 được gọi là điểm cực đại (điểm cực tiểu) của hàm số; f(x0) được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số, kí hiệu là fCÑ (fCT), còn điểm M(x0;f(x0)) được gọi là điểm cực đại (điểm cực tiểu) của đồ thị hàm số.
Các điểm cực đại và cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại (giá trị cực tiểu) còn gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số.
DẠNG 1:Tìm cực trị của hàm số
Quy tắc 1:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Tínhf'(x). Tìm các điểm tại đó f'(x)bằng 0 hoặc f'(x) không xác định.
Bước 3. Lập bảng biến thiên.
Bước 4. Từ bảng biến thiên suy ra các điểm cực trị.
Quy tắc 2:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Tính f'(x). Giải phương trình f'(x)và ký hiệuxi (i=1,2,3,...)là các nghiệm của nó.
Bước 3. Tính f''(x) và f''(xi ) .
Bước 4. Dựa vào dấu của f''(xi )suy ra tính chất cực trị của điểm xi.
DẠNG 2:Tìm tham số m để hàm số đạt cực trị tại một điểm
Trong dạng toán này ta chỉ xét trường hợp hàm số có đạo hàm tại x0.
Khi đó để giải bài toán này, ta tiến hành theo hai bước.
Bước 1. Điều kiện cần để hàm số đạt cực trị tại x0 là y'(x0) = 0, từ điều kiện này ta tìm được giá trị của tham số .
Bước 2. Kiểm lại bằng cách dùng một trong hai quy tắc tìm cực trị ,để xét xem giá trị của tham số vừa tìm được có thỏa mãn yêu cầu của bài toán hay không?
DẠNG 3:Biện luận theo m số cực trị của hàm số
1. Cực trị của hàm số bậc ba
Cho hàm số y = ax3 + bx2 + cx + d, a ≠ 0.
y' = 0 ⇔ 3ax2 + 2bx + c = 0 (1) ; Δ'y' = b2 - 3ac
Phương trình (1) vô nghiệm hoặc có nghiệm kép thì hàm số đã cho không có cực trị.
Hàm số bậc 3 không có cực trị ⇔ b2 - 3ac ≤ 0
Phương trình (1) có hai nghiệm phân biệt thì hàm số đã cho có 2 cực trị.
Hàm số bậc 3 có 2 cực trị ⇔ b2 - 3ac > 0
2. Cực trị của hàm số bậc bốn trùng phương
Cho hàm số: y = ax4 + bx2 + c (a ≠ 0) có đồ thị là (C).
y' = 4ax3 + 2bx; y' = 0 ⇔
(C)có một điểm cực trị y' = 0 có 1 nghiệm x = 0 ⇔ -b/2a ≤ 0 ⇔ ab ≥ 0.
(C)có ba điểm cực trị y' = 0 có 3 nghiệm phân biệt ⇔ -b/2a > 0 ⇔ ab < 0.
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Cực trị của hàm số (mới 2024 + Bài Tập) – Toán 12
Cực trị của hàm số và cách giải các dạng bài tập (2024) mới nhất
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho a và b là hai số thực dương thỏa mãn ab2 = 9. Gía trị của log3a + 2log3b bằng
Câu 2:
Một giá sách hai ngăn có tất cả 108 quyển sách.Sau khi chuyển 8 quyển từ ngăn trên xuống ngăn dưới,rồi lại chuyển 12 quyển từ ngăn dưới lên ngăn trên thì ngăn trên ít hơn ngăn dưới 28 quyển. Vậy: Ngăn dưới có bao nhiêu quyển ; Ngăn trên có bao nhiêu quyển
Câu 3:
Một khung dây hình tròn diện tích S=15cm2 gồm N=10 vòng dây,đặt trong từ trường đều có hợp với véc tơ pháp tuyến của mặt phẳng khung dây một góc =300 như hình vẽ. B=0,04T.Tính độ biến thiên của từ thôngvà độ lớn suất điện động cảm ứng xuất hiện trong khung dây trong thời gian 0,2s khi:
a.Tịnh tiến khung dây trong vùng từ trường đều
b.Quay khung dây quanh đường kính MN một góc 1800
c.Quay khung dây quanh đường kính MN một góc 3600
Câu 4:
Hai ô tô khởi hành cùng một lúc để đi từ Huế vào Đà Nẵng. Tốc độ xe thứ nhất là 40 km/h, tốc độ xe thứ hai là 60 km/h. Xe thứ hai đến Đà Nẵng nghỉ nửa giờ rồi quay lại Huế thì gặp xe thứ nhất ở vị trí cách Đà Nẵng 10 km. Tính quãng đường Huế - Đà Nẵng.
Câu 5:
Giá bìa của cuốn sách là 20.000 đồng. Nhân tháng khai trương, cửa hàng giảm giá xuống còn 15.000 đồng. Hỏi cửa hàng đã giảm giá bao nhiêu phần trăm?
Câu 6:
Quãng đường AB dài 30km. Một người đi xe đạp dự định đi từ A đến B trong thời gian nhất định. Do đường khó đi nên người đi xe đạp đã đi với vận tốc bé hơn vận tốc dự định 5km/h và đã đến B muộn hơn dự định 1 giờ. Tìm vận tốc dự định?
Câu 7:
Quãng đường AD dài 9 km, gồm đoạn AB lên dốc, đoạn BC nằm ngang, đoạn CD xuống dóc. 1 người người đi bộ từ A đến D rồi quay trở về A hết tất cả 3h41'. Tính quãng đường BC, biết vận tốc lúc lên dốc của người đó là 4km/h, lúc xuống dốc là 6km/h và lúc đi nằm ngang là 5km/h
Câu 8:
Hai bến sông A, B cách nhau 200 km. Một ca nô xuôi dòng từ bến A đến bến B rồi ngược từ B trở về A hết tổng thời gian là 9 giờ. Biết thời gian ca nô xuôi dòng 5 km bằng thời gian ca nô ngược dòng 4 km. Tính vận tốc của ca nô khi nước yên lặng và vận tốc của dòng nước
Câu 9:
Để ngâm 3kg mơ thì cần 4kg đường. Hỏi ngâm 2kg mơ thì cần bao nhiêu kg đường?
Câu 11:
Trong không gian với hệ tọa độ Oxyz, cho điểm M(2;3;-4). Tính khoảng cách từ M đến trục Oy
Câu 12:
Một ruột phích có diện tích bề mặt là 0,35 m2. Để tráng được 2000 ruột phích như trên với độ dày lớp bạc là 0,1 thì cần dùng m gam glucose tác dụng với lượng dư dung dịch AgNO3 trong NH3. Biết hiệu suất phản ứng tráng bạc là 70% và khối lượng của bạc là 10,49 g/cm3. Giá trị của m bằng bao nhiêu? Kết quả làm tròn đến hàng đơn vị.
Câu 13:
Cho tam giác ABC vuông tại A ( AB<AC) . Trên cạnh BC lấy điểm K sao cho AB = BK. Gọi H là trumg điểm AK. Kéo dài BH cắt Ac tai I.
a) Nếu góc ABC bằng 60 độ. Tính số đo góc ACB.
b) cm tam giác ABH bằng tam giác ACB. Từ đó suy ra AK vuông góc với BI.
c) Qua K kẻ đường thẳng song song với AC, cắt BH, AB lần lượt tại N và D. cm KA là tia phân giác góc IKD.
d) Kẻ AM vuông góc với BC tại M. cm 3 điểm A,N,M thẳng hàng
Câu 14:
Cho hàm số . Tìm tất cả các giá trị của tham số thực m để hàm số có cực đại mà không có cực tiểu
Câu 15:
Cho tập X = { 1;2;3;4;5 }. Viết ngẫu nhiên lên bảng hai số tự nhiên, mỗi số gồm 3 chữ số đôi một khác nhau thuộc tập X. Tính xác suất để trong hai số đó có đúng một số có chữ số 5