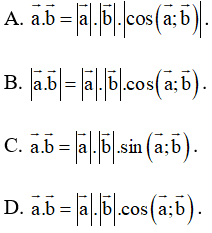Sách bài tập Toán 10 (Cánh diều) Bài ôn tập chương 4
Với giải sách bài tập Toán 10 Bài ôn tập chương 4 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 Bài ôn tập chương 4.
Giải sách bài tập Toán lớp 10 Bài ôn tập chương 4 - Cánh diều
Giải SBT Toán 10 trang 106 Tập 1
Bài 67 trang 106 SBT Toán 10 Tập 1: Cho góc nhọn α. Biểu thức (sinα . cotα)2 + (cosα . tanα)2 bằng:
Lời giải:
Đáp án đúng là C
Ta có: (sinα . cotα)2 + (cosα . tanα)2
= (sinα.cosαsinα)2 + (cosα.sinαcosα)2
= cos2α + sin2α
= 1.
Bài 68 trang 106 SBT Toán 10 Tập 1: Cho các vectơ →a,→b≠→0. Phát biểu nào sau đây là đúng?
Lời giải:
Đáp án đúng là D
Với →a,→b≠→0 ta có: →a.→b=|→a|.|→b|.cos(→a;→b).
Bài 69 trang 106 SBT Toán 10 Tập 1: Cho tứ giác ABCD. Biểu thức →AB.→CD+→BC.→CD+→CA.→CD bằng:
Lời giải:
Đáp án đúng là B
Ta có:
→AB.→CD+→BC.→CD+→CA.→CD=→CD.(→AB+→BC+→CA)
=→CD.(→AC+→CA)
=→CD.→0=0
Bài 70 trang 106 SBT Toán 10 Tập 1: Cho góc nhọn α. Biểu thức tanα . tan(90°– α) bằng:
Lời giải:
Đáp án đúng là C
tanα . tan(90°– α)
= tanα . cotα
= 1.
Lời giải:
Ta có:

a) Vì 0° < α < 90° nên cosα=45
⇒ tanα=sinαcosα=3545=34
⇒ cotα=1tanα=134=43
Áp dụng công thức lượng giác của hai góc bù nhau, ta được:
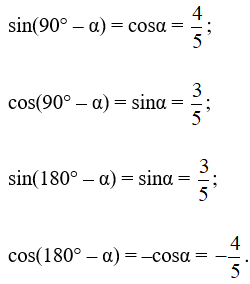
b) Vì 90° < α < 180° nên cosα=−45
⇒ tanα=sinαcosα=35−45=−34
⇒ cotα=1tanα=1−34=−43
Áp dụng công thức lượng giác của hai góc bù nhau, ta được:
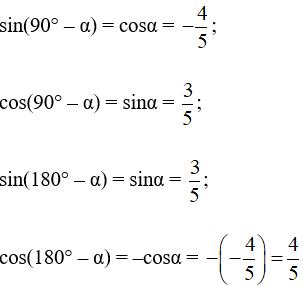
Giải SBT Toán 10 trang 107 Tập 1
a) Độ dài cạnh BC và độ lớn góc B;
b) Bán kính đường tròn ngoại tiếp R;
c) Diện tích của tam giác ABC;
d) Độ dài đường cao xuất phát từ A;
e) →AB.→AC,→AM.→AC với M là trung điểm của BC.
Lời giải:
a) Độ dài cạnh BC và độ lớn góc B;
Xét tam giác ABC, có:
BC2 = AB2 + AC2 – 2AB.AC.cos^BAC
= 42 + 62 – 2.4.6.cos60°
= 42 + 62 – 24
= 28
⇔ BC = √28.
Áp dụng định lí sin trong tam giác ABC ta được:
BCsinA=ACsinB
⇔ sinB=6.sin60°√28≈0,98
⇔ ˆB≈79°.
Vậy BC = √28 và ˆB≈79°.
b) Áp dụng định lí sin trong tam giác, ta có:
BCsinA=2R
⇔ R=BC2sinA=√282sin60°≈3.
Vậy bán kính đường tròn ngoại tiếp tam giác ABC là 3.
c) Áp dụng công thức tính diện tích tam giác, ta được:
SΔABC=12AB.AC.sin^BAC=12.4.6.sin60°=6√3(đvdt)
Vậy diện tích của tam giác ABC là 6√3 (đvdt).
d) Gọi AH là đường cao của tam giác kẻ từ đỉnh A
Ngoài ra diện tích tam giác ABC là:
SΔABC=12BC.AH=12.√28.AH
Theo ý c) ta tính được diện tích tam giác là 6√3
Do đó ta có: 12.√28.AH=6√3
⇔ AH=2.6√3√28≈4
Vậy độ dài đường cao xuất phát từ A là 4.
e) Ta có:
→AB.→AC=|→AB|.|→AC|.cos(→AB,→AC)=4.6.cos60°=12.
Vì M là trung điểm của BC nên →AM=12(→AB+→AC)
Khi đó:
→AM.→AC=12(→AB+→AC).→AC=12→AB.→AC+12.→AC2=12.12+12.62=24
Vậy →AB.→AC=12 và →AM.→AC=24.
Bài 73 trang 107 SBT Toán 10 Tập 1: Cho tam giác ABC. Chứng minh rằng →AB.→AC=12(AB2+AC2−BC2).
Lời giải:
Ta có:
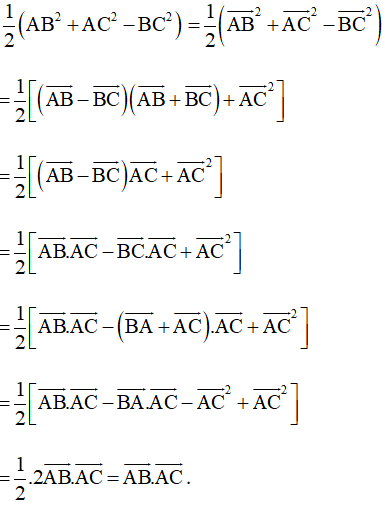
Bài 74 trang 107 SBT Toán 10 Tập 1: Cho tam giác ABC có AB = 5, BC = 6, CA = 7. Tính:
c) Độ dài đường trung tuyến AM.
Lời giải:
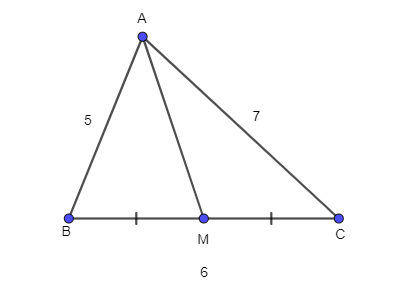
a) Xét tam giác ABC, có:
Áp dụng hệ quả của định lí cosin, ta được:
cos^ABC=AB2+BC2−AC22AB.BC=52+62−722.5.6=15
Ta có: cos2^ABC+sin2^ABC=1
⇔ sin2^ABC=1−cos2^ABC=1−(15)2=2425
Vì ^ABC là góc trong tam giác nên 0°<^ABC<180°
⇒ sin^ABC=2√65.
Vậy sin^ABC=2√65.
b) Diện tích tam giác ABC là:
SΔABC=12AB.BC.sin^ABC=12.5.6.2√65=6√6(đvdt)
Vậy diện tích tam giác ABC là 6√6
c) Vì M là trung điểm của BC nên BM = MC = 12BC = 12.6 = 3.
Xét tam giác ABM:
Áp dụng định lí cos, ta có:
AM2 = AB2 + BM2 – 2.AM.BM.cosB
⇔ AM2 = 52 + 32 – 2.5.3.![]()
⇔ AM2 = 28
⇔ AM = 2√7
Vậy độ dài đường trung tuyến AM là 2√7.
Lời giải:
Ta có: →IA=k→IB⇔→IA−k→IB=→0
Xét vế phải của đẳng thức ta có:
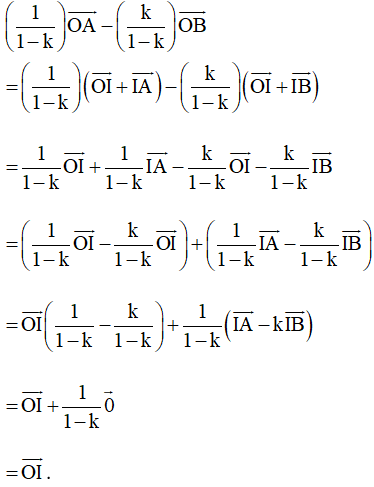
Lời giải:
Ta có:
→AB.→AC=AB.AC.cos(→AB,→AC)=4.5.cos120°=−10
Ta lại có: →AM=12(→AB+→AC)
Và →BD=→BA+→AD=−→AB+25→AC
⇒→AM.→BD=12(→AB+→AC).(−→AB+25→AC)
⇔ →AM.→BD=−12→AB2+15→AB.→AC−12→AC.→AB+15→AC2
⇔ →AM.→BD=−12.42+15(−10)−12(−10)+15.52=0
Suy ra AM vuông góc BD.
Vậy →AB.→AC=−10 và AM vuông góc BD.
Lời giải:
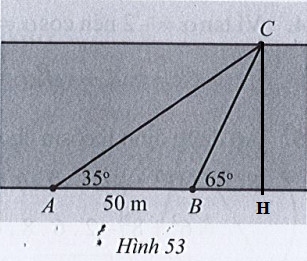
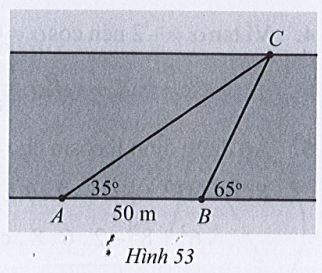
Kẻ CH vuông góc với bờ AB.
Xét tam giác ABC, có:
^ABC+^BAC+^ACB=180°
⇒ ^ACB=180°−(^ABC+^BAC)=180°−(35°+115°)=30°
Áp dụng định lí sin trong tam giác, ta được:
ABsin^ACB=BCsin^CAB
⇔50sin30°=BCsin35°
⇔BC=50sin35°sin30°≈57,36
Xét tam giác CHB vuông tại B, có:
sin^CBH=CHBC⇔CH=sin^CBH.BC≈sin65°.57,36≈51,98.
Vậy độ rộng của con sông chỗ chảy qua vị trí người quan sát khoảng 51,98 mét.
Lời giải:
(→a+2→b)(2→a−→b)=2→a2−→a.→b+4→a.→b−2→b2=2→a2+3→a.→b−2→b2
=2→a2+3|→a|.|→b|.cos(→a,→b)−2→b2
=2.42+3.4.5.cos135°−2.52=−18−30√2
Giải SBT Toán 10 trang 108 Tập 1
b) Cho |→a|=2,|→b|=3,|→a+→b|=√7. Tính →a.→b và (→a,→b).
Lời giải:
a)
|→a+→b|2=(→a+→b)2=→a2+→b2+2.→a.→b=|→a|2+|→b|2+2.→a.→b
b) Áp dụng công thức trên ta được:
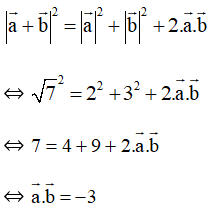
Mặt khác ta lại có:
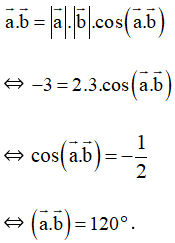
Vậy →a.→b=−3 và (→a.→b)=120°.
Lời giải:
Ta có: →AD.→BC+→BE.→CA+→CF.→AB
= 12(→AB+→AC).→BC+12(→BA+→BC).→CA+12(→CA+→CB).→AB
= 12→AB.→BC+12→AC.→BC+12→BA.→CA+12→BC.→CA+12→CA.→AB+12→CB.→AB
= (12→AB.→BC+12→CB.→AB)+(12→AC.→BC+12→BC.→CA)+(12→BA.→CA+12→CA.→AB)
= 0
Lời giải:
Gọi I và J lần lượt là trung điểm của AB và CD.
Khi đó ta có: →IA+→IB=→0 và →JC+→JD=→0
⇒ (→MA+→MB). (→MC+→MD)=(→MI+→IA+→MI+→IB). (→MJ+→JC+→MJ+→JD)=→0
⇔(→MI+→IA+→MI+→IB). (→MJ+→JC+→MJ+→JD)=→0
⇔(2→MI+→IA+→IB). (2→MJ+→JC+→JD)=→0
⇔4→MI. →MJ=→0
⇔ ^IMJ=90°
Vậy M là điểm thuộc đường tròn đường kính IJ.
Lời giải:
Xét biểu thức →MA+→MB+→MC=→MG+→GA+→MG+→GB+→MG+→GC
=3→MG+(→GA+→GB+→GC)
=3→MG
⇒|→MA+→MB+→MC|=|3→MG|
Do đó để biểu thức |→MA+→MB+→MC| đạt giá trị nhỏ nhất thì |3→MG| đạt giá trị nhỏ nhất khi MG nhỏ nhất và MG nhỏ nhất khi M là hình chiếu vuông góc của G lên đường thẳng d.
Vậy để |→MA+→MB+→MC| đạt giá trị nhỏ nhất thì điểm M là hình chiếu vuông góc của G trên đường thẳng d.
Xem thêm lời giải sách bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:
Bài 2: Giải tam giác. Tính diện tích tam giác
Bài 4: Tổng và hiệu của hai vectơ
Bài 5: Tích của một số với một vectơ
Bài 6: Tích vô hướng của hai vectơ
Xem thêm tài liệu Toán lớp 10 Cánh diều hay, chi tiết khác:
Xem thêm các chương trình khác:
- Soạn văn lớp 10 (hay nhất) – Cánh Diều
- Tác giả tác phẩm Ngữ văn lớp 10 – Cánh Diều
- Tóm tắt tác phẩm Ngữ văn lớp 10 – Cánh Diều
- Bố cục tác phẩm Ngữ văn lớp 10 – Cánh Diều
- Nội dung chính tác phẩm Ngữ văn lớp 10 – Cánh Diều
- Soạn văn lớp 10 (ngắn nhất) – Cánh Diều
- Giải sbt Ngữ văn lớp 10 – Cánh Diều
- Văn mẫu lớp 10 – Cánh Diều
- Giải Chuyên đề học tập Ngữ văn 10 – Cánh diều
- Giải sgk Tiếng Anh 10 – Explore new worlds
- Giải sgk Tiếng Anh 10 – ilearn Smart World
- Trọn bộ Từ vựng Tiếng Anh 10 ilearn Smart World đầy đủ nhất
- Ngữ pháp Tiếng Anh 10 i-learn Smart World
- Giải sbt Tiếng Anh 10 - iLearn Smart World
- Giải sgk Vật lí 10 – Cánh Diều
- Giải sbt Vật lí 10 – Cánh Diều
- Lý thuyết Vật lí 10 – Cánh Diều
- Giải Chuyên đề Vật lí 10 – Cánh Diều
- Giải sgk Hóa học 10 – Cánh Diều
- Lý thuyết Hóa học 10 – Cánh Diều
- Giải sbt Hóa học 10 – Cánh Diều
- Giải Chuyên đề Hóa học 10 – Cánh Diều
- Giải sgk Sinh học 10 – Cánh Diều
- Giải sbt Sinh học 10 – Cánh Diều
- Lý thuyết Sinh học 10 – Cánh Diều
- Giải Chuyên đề Sinh học 10 – Cánh diều
- Giải sgk Lịch sử 10 – Cánh Diều
- Giải sbt Lịch sử 10 – Cánh Diều
- Giải Chuyên đề Lịch sử 10 – Cánh Diều
- Lý thuyết Lịch sử 10 – Cánh diều
- Giải sgk Địa lí 10 – Cánh Diều
- Lý thuyết Địa Lí 10 – Cánh Diều
- Giải sbt Địa lí 10 – Cánh Diều
- Giải Chuyên đề Địa lí 10 – Cánh Diều
- Lý thuyết Công nghệ 10 – Cánh Diều
- Giải sgk Công nghệ 10 – Cánh Diều
- Giải sgk Giáo dục Kinh tế và Pháp luật 10 – Cánh Diều
- Giải sbt Giáo dục Kinh tế và Pháp luật 10 – Cánh Diều
- Giải Chuyên đề Kinh tế pháp luật 10 – Cánh diều
- Lý thuyết KTPL 10 – Cánh diều
- Lý thuyết Giáo dục quốc phòng 10 – Cánh Diều
- Giải sgk Giáo dục quốc phòng - an ninh 10 – Cánh diều
- Giải sbt Giáo dục quốc phòng - an ninh 10 – Cánh Diều
- Giải sgk Hoạt động trải nghiệm 10 – Cánh Diều
- Giải sbt Hoạt động trải nghiệm 10 – Cánh Diều
- Giải sgk Tin học 10 – Cánh Diều
- Giải sbt Tin học 10 – Cánh Diều
- Giải Chuyên đề Tin học 10 – Cánh diều
- Lý thuyết Tin học 10 - Cánh diều
- Giải sgk Giáo dục thể chất 10 – Cánh Diều