Sách bài tập Toán 10 Bài 4 (Cánh diều): Bất phương trình bậc nhất một ẩn

Giải sách bài tập Toán lớp 10 Bài 4: Bất phương trình bậc nhất một ẩn - Cánh diều

Giải SBT Toán 10 trang 56 Tập 1

Bài 28 trang 56 SBT Toán 10 Tập 1: Trong các bất phương tình sau, bất phương trình nào không là bất phương trình bậc nhất một ẩn?

A.  – 2x² + 3x < 0;

B. 0,5y² – $\sqrt{3}$(y – 2) ≤ 0;

C. x² – 2xy – 3 ≥ 0;

D. $\sqrt{2}$x² – 3 ≥ 0.

Lời giải

Đáp án đúng là C

Xét bất phương trình  – 2x² + 3x < 0 là bất phương trình bậc hai một ẩn x. Do đó A sai.

Xét bất phương trình 0,5y² – $\sqrt{3}$(y – 2) ≤ 0 ⇔ 0,5y² – $\sqrt{3}$y + 2$\sqrt{3}$ ≤ 0 là bất phương trình bậc hai một ẩn y. Do đó B sai.

Xét bất phương trình x² – 2xy – 3 ≥ 0 là bất phương trình bậc hai nhưng lại có hai ẩn x và y. Do đó C đúng.

Xét bất phương trình $\sqrt{2}$x² – 3 ≥ 0 là bất phương trình bậc hai một ẩn x. Do đó D sai.

Bài 29 trang 56 SBT Toán 10 Tập 1: Tập nghiệm của bất phương trình  – x² + 3x + 18 ≥ 0 là:

A. [ – 3; 6];

B. (– 3; 6);

C. (– ∞; – 3) ∪ (6; +∞);

D. (– ∞; – 3] ∪ [6; +∞).

Lời giải

Đáp án đúng là A

Xét f(x) = – x² + 3x + 18 là một tam thức bậc hai có a = – 1 < 0 và ∆ = 3² – 4.(– 1).18 = 81 > 0.

Do đó f(x) có hai nghiệm phân biệt là x₁ = – 3 và x₂ = 6.

Theo định lí về dấu tam thức bậc hai, ta có:

f(x) > 0 khi x ∈ (– 3; 6);

f(x) < 0 khi x ∈ (–∞; – 3) ∪ (6; +∞);

Suy ra f(x) ≥ 0 khi x ∈ [– 3; 6].

Vậy tập nghiệm của bất phương trình là S = [– 3; 6].

Bài 30 trang 56 SBT Toán 10 Tập 1: Dựa vào đồ thị hàm số bậc hai y = f(x) trong mỗi Hình 18a, 18b, 18c, hãy viết tập nghiệm các bất phương trình sau: f(x) > 0; f(x) < 0; f(x) ≥ 0 và f(x) ≤ 0.

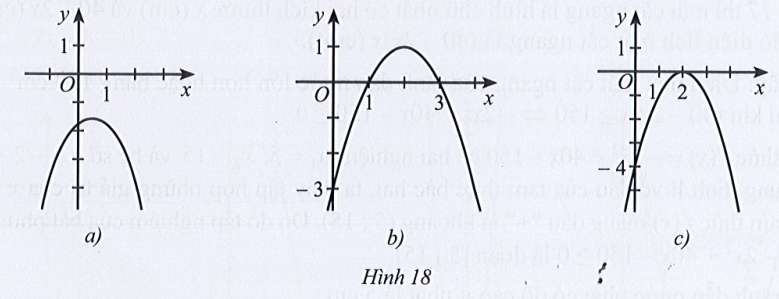
Lời giải

+) Hình 18a):

Quan sát đồ thị hàm số, ta thấy:

Đồ thị hàm số nằm hoàn toàn phía dưới trục hoành với mọi x ∈ ℝ.

Do đó:

f(x) < 0 và f(x) ≤ 0 luôn đúng với mọi x ∈ ℝ.

f(x) > 0; f(x) ≥ 0 và vô nghiệm.

Vậy tập nghiệm của các bất phương trình f(x) > 0 và f(x) ≥ 0 là $\varnothing$, tập nghiệm của bất phương trình f(x) < 0 và f(x) ≤ 0 là ℝ.

+) Hình 18b):

Quan sát đồ thị hàm số, ta thấy:

Với x ∈ (1; 3) hàm số nằm trên trục hoành hay f(x) > 0.

Với x < 1 hoặc x > 3 đồ thị hàm số nằm phía dưới trục hoành hay f(x) < 0.

Đồ thị hàm số cắt trục hoành tại x = 1 hoặc x = 3.

Do đó:

f(x) > 0 khi x ∈ (1; 3).

f(x) < 0 khi x ∈ (– ∞; 1) ∪ (3; +∞).

f(x) ≥ 0 khi x ∈ [1; 3].

f(x) ≤ 0 khi x ∈ (– ∞; 1] ∪ [3; +∞).

Vậy tập nghiệm của các bất phương trình f(x) > 0; f(x) < 0; f(x) ≥ 0; f(x) ≤ 0 lần lượt là (1; 3); (– ∞; 1) ∪ (3; +∞); [1; 3]; (– ∞; 1] ∪ [3; +∞).

+) Hình 18c):

Quan sát đồ thị hàm số, ta thấy:

Đồ thị hàm số cắt trục hoành tại x = 2.

Với x ≠ 2 hàm số nằm dưới trục hoành hay f(x) < 0.

Do đó:

f(x) > 0 vô nghiệm.

f(x) < 0 khi x ∈ ℝ \ {2}.

f(x) ≥ 0 khi x = 2.

f(x) ≤ 0 khi x ∈ ℝ.

Vậy tập nghiệm của các bất phương trình f(x) > 0; f(x) < 0; f(x) ≥ 0; f(x) ≤ 0 lần lượt là $\varnothing$; ℝ \ {2}; {2}; ℝ.

Bài 31 trang 56 SBT Toán 10 Tập 1: Giải các bất phương trình bậc hai sau:

a) 3x² – 8x + 5 > 0;

b) – 2x² – x + 3 ≤ 0;

c) 25x² – 10x + 1 < 0;

d) – 4x² + 5x + 9 ≥ 0.

Lời giải

a) Xét tam thức bậc hai f(x) = 3x² – 8x + 5, có a = 3, ∆ = (– 8)² – 4.3.5 = 4 > 0

Suy ra tam thức bậc hai có hai nghiệm x₁ = 1 và x₂ =$\frac{5}{3}$.

Áp dụng định lí dấu của tam thức bậc hai, ta có:

f(x) > 0 khi x ∈ $\left(-\infty ;1\right)\cup \left(\frac{5}{3};+\infty \right)$;

f(x) < 0 khi x ∈ $\left(1;\frac{5}{3}\right)$.

Suy ra 3x² – 8x + 5 > 0 khi x ∈ $\left(-\infty ;1\right)\cup \left(\frac{5}{3};+\infty \right)$.

Vậy tập nghiệm của bất phương trình 3x² – 8x + 5 > 0 là $\left(-\infty ;1\right)\cup \left(\frac{5}{3};+\infty \right)$.

b) Xét tam thức bậc hai g(x) =  – 2x² – x + 3, có a = – 2 < 0 và ∆ = (– 1)² – 4.(– 2).3 = 25 > 0.

Do đó tam thức có hai nghiệm phân biệt x₁ = 1 và x₂ =$\frac{-3}{2}$.

Áp dụng định lí về dấu của tam thức bậc hai ta có:

g(x) > 0 khi x ∈ $\left(-\frac{3}{2};1\right)$;

g(x) < 0 khi x ∈ $\left(-\infty ;-\frac{3}{2}\right)\cup \left(1;+\infty \right)$.

Suy ra  – 2x² – x + 3 ≤ 0 khi x ∈ $\left(-\infty ;-\frac{3}{2}\right]\cup \left[1;+\infty \right)$.

Vậy tập nghiệm của bất phương trình đã cho là S = $\left(-\infty ;-\frac{3}{2}\right]\cup \left[1;+\infty \right)$.

c) Xét tam thức bậc hai h(x) =  25x² – 10x + 1, có a = 25 > 0 và ∆ = (– 10)² – 4.25.1 = 0.

Do đó tam thức có nghiệm kép là x = $\frac{1}{5}$.

Áp dụng định lí về dấu của tam thức bậc hai ta có:

h(x) > 0 khi x ≠ $\frac{1}{5}$.

Suy ra  25x² – 10x + 1 < 0 khi x ∈ $\varnothing$.

Vậy tập nghiệm của bất phương trình đã cho là S = $\varnothing$.

d) Xét tam thức bậc hai k(x) =  – 4x² + 5x + 9 , có a = – 4 < 0 và ∆ = 5² – 4.(– 4).9 = 169 > 0.

Do đó tam thức có hai nghiệm phân biệt là x₁ = – 1 và x₂ = $\frac{9}{4}$.

Áp dụng định lí về dấu của tam thức bậc hai ta có:

k(x) < 0 khi x ∈ $\left(-\infty ;-1\right)\cup \left(\frac{9}{4};+\infty \right)$;

k(x) > 0 khi x ∈ $\left(-1;\frac{9}{4}\right)$.

Suy ra – 4x² + 5x + 9 ≥ 0 khi x ∈ $\left[-1;\frac{9}{4}\right]$.

Vậy tập nghiệm của bất phương trình đã cho là S = $\left[-1;\frac{9}{4}\right]$.

Giải SBT Toán 10 trang 57 Tập 1

Bài 32 trang 57 SBT Toán 10 Tập 1: Tìm giao các tập nghiệm của hai bất phương trình – 3x² + 7x + 10 ≥ 0 và – 2x² – 9x + 11 > 0.

Lời giải

Xét tam thức bậc hai f(x) =  – 3x² + 7x + 10, có a = – 3 < 0 và ∆ = 7² – 4.(– 3).10 = 169 > 0.

Do đó tam thức có hai nghiệm phân biệt là x₁ = – 1 và x₂ = $\frac{10}{3}$.

Áp dụng định lí về dấu của tam thức bậc hai ta có:

f(x) < 0 khi x ∈ $\left(-\infty ;-1\right)\cup \left(\frac{10}{3};+\infty \right)$;

f(x) > 0 khi x ∈ $\left(-1;\frac{10}{3}\right)$.

Suy ra tập nghiệm của bất phương trình – 3x² + 7x + 10 ≥ 0 là S₁ = $\left[-1;\frac{10}{3}\right]$.

Xét tam thức bậc hai g(x) =  – 2x² – 9x + 11, có a = – 2 < 0 và ∆ = (– 9)² – 4.(– 2).11 = 169 > 0.

Do đó tam thức có hai nghiệm phân biệt là x₁ = 1 và x₂ = $-\frac{11}{2}$.

Áp dụng định lí về dấu của tam thức bậc hai ta có:

g(x) < 0 khi x ∈ $\left(-\infty ;-\frac{11}{2}\right)\cup \left(1;+\infty \right)$;

g(x) > 0 khi x ∈ $\left(-\frac{11}{2};1\right)$.

Suy ra tập nghiệm của bất phương trình – 2x² – 9x + 11 > 0 là S₂ = $\left(-\frac{11}{2};1\right)$.

Đặt S = S₁ ∩ S₂ = $\left[-1;\frac{10}{3}\right]\cap \left(-\frac{11}{2};1\right)$.

Ta có hình vẽ sau:

Vậy giao của hai tập nghiệm của hai bất phương trình trên là S = [ – 1; 1).

Bài 33 trang 57 SBT Toán 10 Tập 1: Tìm m để phương trình – x² + (m + 2)x + 2m – 10 = 0 có nghiệm.

Lời giải

Xét phương trình – x² + (m + 2)x + 2m – 10 = 0 có ∆ = (m + 2)² – 4.(– 1).(2m – 10) = m² + 12m – 36.

Để phương trình đã cho có nghiệm thì ∆ ≥ 0 ⇔ m² + 12m – 36 ≥ 0

Xét tam thức bậc hai f(m) = m² + 12m – 36, có a = 1, ∆_m = 12² – 4.1.(– 36) = 288 > 0.

Do đó tam thức có hai nghiệm phân biệt m₁ = $-6-6\sqrt{2}$ và m₁ = $-6+6\sqrt{2}$.

Áp dụng định lí về dấu của tam thức bậc hai ta có: f(m) ≥ 0 khi m ∈$\left(-\infty ;-6-6\sqrt{2}\right)\cup \left(-6+6\sqrt{2};+\infty \right)$.

Vậy m ∈$\left(-\infty ;-6-6\sqrt{2}\right)\cup \left(-6+6\sqrt{2};+\infty \right)$ thì phương trình đã cho có nghiệm.

Bài 34 trang 57 SBT Toán 10 Tập 1: Xét hệ tọa độ Oth trong mặt phẳng, trong đó trục Ot biểu thị thời gian t (tính bằng giây) và trục Oh biểu thị độ cao h (tính bằng mét). Một quả bóng được đá lên từ điểm A(0; 0,3) và chuyển động theo quỹ đạo là một cung parabol. Quả bóng đạt độ cao 8m sau 1 giây và đạt độ cao 6m sau 2 giây. Trong khoảng thời gian nào (tính bằng giây) thì quả bóng ở độ cao lớn hơn 5m và nhỏ hơn 7m (làm tròn kết quả đến hàng phần nghìn).

Lời giải

Ta có hình vẽ mô phỏng quỹ đạo chuyển động của quả bóng như hình vẽ:

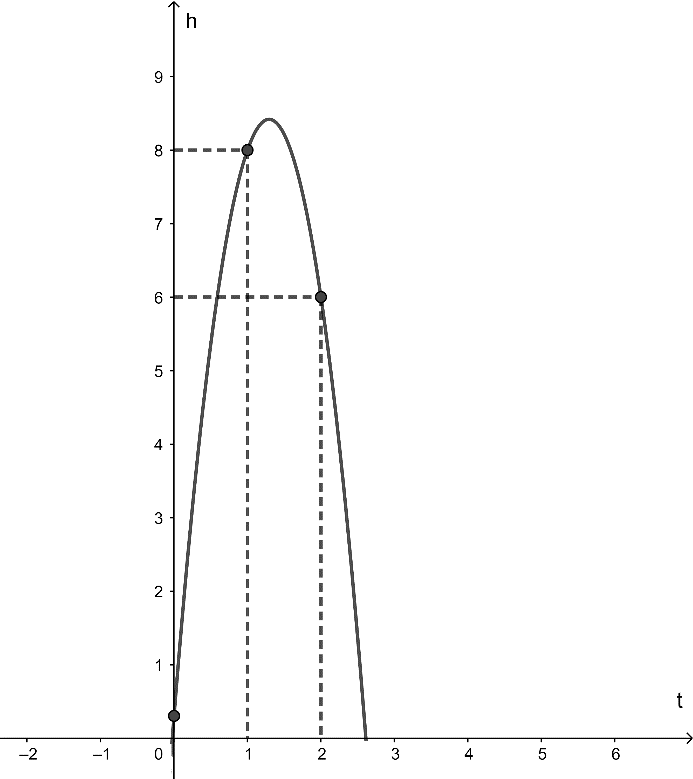
Vì quỹ đạo chuyển động là một đường thẳng parabol có dạng h = at² + bt + c (a ≠ 0).

Một quả bóng được đá lên từ điểm A(0; 0,3) nên điểm A thuộc vào parabol, thay t = 0 và h = 0,3 vào đồ thị hàm số ta được: 0,3 = a.0² + b.0 + c ⇔ c = 0,3 (1).

Bóng đạt độ cao h = 8m sau t = 1 giây nên điểm có tọa độ (1; 8) thuộc vào parabol.

Thay t = 1 và h = 8 vào đồ thị hàm số ta được: 8 = a.1² + b.1 + c ⇔ a + b + c = 8 (2).

Bóng đạt độ cao h = 6m sau t = 2 giây nên điểm có tọa độ (2; 6) thuộc vào parabol.

Thay t = 2 và h = 6 vào đồ thị hàm số ta được: 6 = a.2² + b.2 + c ⇔ 4a + 2b + c = 6 (3).

Từ (1), (2) và (3) ta có hệ phương trình: $\left\{\begin{array}{l}c=0,3\\ a+b+c=8\\ 4a+2b+c=6\end{array}\right.\iff \left\{\begin{array}{l}c=0,3\\ a=-4,85\\ b=12,55\end{array}\right.$.

Ta có phương trình parabol cần tìm là: h = – 4,85t² + 12,55t + 0,3.

Để chiều cao lớn hơn 5 thì h > 5 ⇔ – 4,85t² + 12,55t + 0,3 > 5

⇔ – 4,85t² + 12,55t – 4,7 > 0

Xét tam thức bậc hai f(t) = – 4,85t² + 12,55t – 4,7, có a = – 4,85, ∆ = 12,55² – 4.(– 4,85).(– 4,7) = 66,3225 > 0.

Suy ra tam thức có hai nghiệm phân biệt t₁ ≈ 0,454 và t₂ ≈ 2,133.

Áp dụng định lí về dấu của tam thức bậc hai ta được: f(t) > 0 hay – 4,85t² + 12,55t – 4,7 > 0 khi t ∈ (0,454; 2,133).

Để chiều cao nhỏ hơn 7 thì h < 7 ⇔ – 4,85t² + 12,55t + 0,3 < 7

⇔ – 4,85t² + 12,55t – 6,7 < 0

Xét tam thức bậc hai g(t) = – 4,85t² + 12,55t – 6,7, có a = – 4,85, ∆ = 12,55² – 4.(– 4,85).(– 6,7) = 27,5225 > 0.

Suy ra tam thức có hai nghiệm phân biệt t₁ ≈ 0,753 và t₂ ≈ 1,835.

Áp dụng định lí về dấu của tam thức bậc hai ta được: g(t) < 0 hay – 4,85t² + 12,55t – 6,7 < 0 khi t ∈ (– ∞; 0,753) ∪ (1,835; +∞).

Để quả bóng ở độ cao lớn hơn 5m và nhỏ hơn 7m thì t phải thuộc vào giao của hai tập (0,454; 2,133) hoặc (– ∞; 0,753) ∪ (1,835; +∞).

Ta có (0,454; 2,133)  (– ∞; 0,753) ∪ (1,835; +∞) = (0,454; 0,753) ∪ (1,835; 2,133).

Vậy để quả bóng ở độ cao lớn hơn 5m và nhỏ hơn 7m thì thuộc khoảng 0,454 giây đến 0,753 giây hoặc 1,835 giây đến 2,133 giây.

Bài 35 trang 57 SBT Toán 10 Tập 1: Một tình huống trong huấn luyện pháo binh được mô tả như sau: Trong mặt phẳng tọa độ Oxy (đơn vị trên hai trục tính theo mét), một viên đạn được bắn từ vị trí O(0; 0) theo quỹ đạo là đường parabol y = $-\frac{9}{1000000}{x}^2+\frac{3}{100}x$. Tìm khoảng cách theo trục hoành của viên đạn so với vị trí bắn khi viên đạn đang ở độ cao hơn 15m (làm tròn kết quả đến hàng phần trăm theo đơn vị mét).

Lời giải

Viên đạn đang ở độ cao hơn 15m nghĩa là: $-\frac{9}{1000000}{x}^2+\frac{3}{100}x$ > 15

$\iff -\frac{9}{1000000}{x}^2+\frac{3}{100}x-15>0$ 

Xét tam thức f(x) = $-\frac{9}{1000000}{x}^2+\frac{3}{100}x-15$, có a = $-\frac{9}{1000000}$ và

∆ = ${\left(\frac{3}{100}\right)}^2-4.\left(-\frac{9}{1000000}\right).\left(-15\right)=\frac{9}{25000}$ > 0.

Do đó tam thức có hai nghiệm phân biệt x₁ ≈ 2 720,76 và x₂ ≈ 612,57.

Áp dụng định lí về dấu ta có: f(x) > 0 hay $-\frac{9}{1000000}{x}^2+\frac{3}{100}x>15$ khi x ∈ (612,57; 2 720,76).

Vậy khi viên đạn đang ở độ cao hơn 15m thì có khoảng cách đến vị trí bắn trong khoảng 612,57 m đến 2 720,76 m.

Xem thêm lời giải sách bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

Bài ôn tập chương 2

Bài 1: Hàm số và đồ thị

Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng

Bài 3: Dấu của tam thức bậc hai

Bài 5: Hai dạng phương trình quy về phương trình bậc hai

Xem thêm tài liệu Toán lớp 10 Cánh diều hay, chi tiết khác:

Lý thuyết Bài 4. Bất phương trình bậc hai một ẩn