Sách bài tập Toán 10 Bài 3 (Cánh diều): Các số đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm

Giải sách bài tập Toán lớp 10 Bài 3: Các số đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm - Cánh diều

Giải SBT Toán 10 trang 37 Tập 2

Bài 14 trang 37 SBT Toán 10 Tập 2:

Cho mẫu số liệu:     21     22     23     24     25

a) Khoảng biến thiên của mẫu số liệu trên là:

A. 1.

B. 2.

C. 3.

D. 4.

b) Khoảng tứ phân vị của mẫu số liệu trên là:

A. 1.

B. 2.

C. 3.

D. 4.

c) Phương sai của mẫu số liệu trên là:

A. 1.

B. 2.

C. 3.

D. 4.

d) Độ lệch chuẩn của mẫu số liệu trên là:

A. 1.

B. $\sqrt{2}$ .

C. $\sqrt{3}$ .

D. 4.

Lời giải:

a) Trong mẫu số liệu trên, số lớn nhất là 25 và số nhỏ nhất là 21.

Vậy khoảng biến thiên của mẫu số liệu trên là: R = x_max – x_min = 25 – 21 = 4.

Do đó ta chọn phương án D.

b) Mẫu số liệu trên đã được sắp xếp theo thứ tự không giảm.

Trung vị của mẫu số liệu trên là: M_e = 23.

Trung vị của dãy 21; 22 là: $\frac{21+22}{2}=\mathrm{21,5}$ .

Trung vị của dãy 24; 25 là: $\frac{24+25}{2}=\mathrm{24,5}$ .

Suy ra Q₁ = 21,5; Q₂ = 23; Q₃ = 24,5.

Do đó khoảng tứ phân vị của mẫu số liệu trên là: ∆_Q = Q₃ – Q₁ = 24,5 – 21,5 = 3.

Vậy ta chọn phương án C.

c) Số trung bình cộng của mẫu số liệu trên là: $\overline{x}=\frac{21+22+23+24+25}{5}=23$ .

Ta có (21 – 23)² + (22 – 23)² + (23 – 23)² + (24 – 23)² + (25 – 23)² = 10.

Phương sai của mẫu số liệu trên là: $s^2=\frac{10}{5}=2$ .

Vậy ta chọn phương án B.

d) Độ lệch chuẩn của mẫu số liệu trên là: $s=\sqrt{s^2}=\sqrt{2}$ .

Vậy ta chọn phương án B.

Giải SBT Toán 10 trang 38 Tập 2

Bài 15 trang 38 SBT Toán 10 Tập 2:

Biểu đồ đoạn thẳng ở Hình 2 biểu diễn thu nhập bình quân đầu người/năm của Việt Nam ở một số năm trong giai đoạn từ 1986 đến 2020.

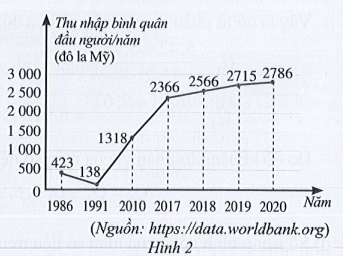
Mẫu số liệu nhận được từ biểu đồ ở Hình 2 có khoảng biến thiên là bao nhiêu?

A. 71.

B. 85.

C. 1 180.

D. 2 648.

Lời giải:

Mẫu số liệu thống kê thu nhập bình quân đầu người/năm nhận được từ biểu đồ trên là:

423     138     1318     2366     2566     2715     2786

Trong mẫu số liệu trên, số lớn nhất là 2786 và số nhỏ nhất là 138.

Vậy khoảng biến thiên của mẫu số liệu trên là: R = x_max – x_min = 2786 – 138 = 2648.

Do đó ta chọn phương án D.

Bài 16 trang 38 SBT Toán 10 Tập 2:

Biểu đồ đoạn thẳng ở Hình 3 biểu diễn số lượt khách vào một cửa hàng trong ngày đầu khai trương tại một số mốc thời gian.

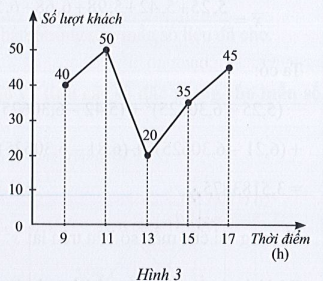
Mẫu số liệu nhận được từ biểu đồ ở Hình 3 có khoảng tứ phân vị là bao nhiêu?

A. 10.

B. 15.

C. 20.

D. 5.

Lời giải:

Mẫu số liệu thống kê số lượt khách vào một cửa hàng trong ngày đầu khai trương nhận được từ biểu đồ trên là:

40     50     20     35     45

Sắp xếp mẫu số liệu trên theo thứ tự không giảm, ta được dãy:

20     35     40     45     50

Trung vị của mẫu số liệu trên là: M_e = 40.

Trung vị của dãy 20; 35 là: $\frac{20+35}{2}=\mathrm{27,5}$ .

Trung vị của dãy 45; 50 là: $\frac{45+50}{2}=\mathrm{47,5}$ .

Vậy Q₁ = 27,5; Q₂ = 40; Q₃ = 47,5.

Suy ra khoảng tứ phân vị của mẫu số liệu trên là: ∆_Q = Q₃ – Q₁ = 47,5 – 27,5 = 20.

Do đó ta chọn phương án C.

Bài 17 trang 38 SBT Toán 10 Tập 2:

Cho mẫu số liệu:     1     11     13     15     17       21

a) Tìm khoảng biến thiên của mẫu số liệu trên.

b) Tìm khoảng tứ phân vị của mẫu số liệu trên.

c) Tính phương sai và độ lệch chuẩn của mẫu số liệu trên.

d) Tìm giá trị bất thường của mẫu số liệu trên.

Lời giải:

a) Trong mẫu số liệu trên, số lớn nhất là 21 và số nhỏ nhất là 1.

Vậy khoảng biến thiên của mẫu số liệu trên là: R = x_max – x_min = 21 – 1 = 20.

b) Mẫu số liệu trên đã được sắp xếp theo thứ tự không giảm.

Trung vị của mẫu số liệu trên là: $\frac{13+15}{2}=14$ .

Trung vị của dãy 1; 11; 13 là: 11.

Trung vị của dãy 15; 17; 21 là 17.

Vậy Q₁ = 11; Q₂ = 14; Q₃ = 17.

Do đó khoảng tứ phân vị của mẫu số liệu trên là: ∆_Q = Q₃ – Q₁ = 17 – 11 = 6.

c) Số trung bình cộng của mẫu số liệu trên là: $\overline{x}=\frac{1+11+13+15+17+21}{6}=13$ .

Ta có (1 – 13)² + (11 – 13)² + (13 – 13)² + (15 – 13)² + (17 – 13)² + (21 – 13)² = 232.

Phương sai của mẫu số liệu trên là: $s^2=\frac{232}{6}=\frac{116}{3}$ .

Độ lệch chuẩn của mẫu số liệu trên là: $s=\sqrt{s^2}=\sqrt{\frac{116}{3}}=\frac{2\sqrt{87}}{3}$ .

d) Ta có:

⦁ $Q_1-\frac{3}{2}{\Delta }_Q=11-\frac{3}{2}.6=2$ ;

⦁ $Q_3+\frac{3}{2}{\Delta }_Q=17+\frac{3}{2}.6=26$ .

Ta thấy 1 < 2.

Vậy 1 là giá trị bất thường của mẫu số liệu đã cho.

Bài 18 trang 38 SBT Toán 10 Tập 2:

Kết quả dự báo nhiệt độ cao nhất trong 10 ngày liên tiếp ở Nghệ An cuối tháng 01 năm 2022 được cho ở bảng sau:

(Nguồn: https://nchmf.gov.vn)

a) Viết mẫu số liệu thống kê nhiệt độ nhận được từ bảng trên.

b) Tính số trung bình cộng, phương sai và độ lệch chuẩn của mẫu số liệu đó.

Lời giải:

a) Mẫu số liệu thống kê nhiệt độ nhận được từ bảng trên là:

23     25     26     27     27     27     27     21     19     18

b) Số trung bình cộng của mẫu số liệu trên là:

$\overline{x}=\frac{23+25+26+27+27+27+27+21+19+18}{10}=24$ (°C)

Ta có (23 – 24)² + (25 – 24)² + (26 – 24)² + (27 – 24)² + (27 – 24)² + (27 – 24)²

+ (27 – 24)² + (21 – 24)² + (19 – 24)² + (18 – 24)² = 112.

Phương sai của mẫu số liệu trên là: $s^2=\frac{112}{10}=\mathrm{11,2}$ .

Độ lệch chuẩn của mẫu số liệu trên là: $s=\sqrt{s^2}=\sqrt{\mathrm{11,2}}=\frac{2\sqrt{70}}{5}$  (°C).

Bài 19 trang 38 SBT Toán 10 Tập 2:

Biểu đồ đoạn thẳng ở Hình 4 cho biết kết quả thi Ngoại ngữ ở câu lạc bộ của Dũng (đường nét liền) và Hoàng (đường nét đứt đậm) qua 9 lần kiểm tra.

a) Viết mẫu số liệu thống kê kết quả thi ngoại ngữ của Dũng và Hoàng nhận được từ biểu đồ ở Hình 4.

b) Tìm khoảng biến thiên và khoảng tứ phân vị của mỗi mẫu số liệu đó.

c) Tính phương sai và độ lệch chuẩn của hai mẫu số liệu đó. Cho biết kết quả thi của bạn nào ổn định hơn?

Lời giải:

a) Mẫu số liệu thống kê kết quả thi ngoại ngữ của Dũng là:

8     9     7     9     7     8     8     7     9     (1)

Mẫu số liệu thống kê kết quả thi ngoại ngữ của Hoàng là:

6     10     8     8     7     9     6     9     8     (2)

b) Xét mẫu số liệu (1):

⦁ Trong mẫu số liệu (1), số điểm lớn nhất là 9 và số điểm thấp nhất là 7.

Do đó khoảng biến thiên của mẫu số liệu (1) là: R = x_max – x_min = 9 – 7 = 2.

⦁ Sắp xếp mẫu số liệu (1) theo thứ tự không giảm, ta được dãy:

7     7     7     8     8     8     9     9     9

Trung vị của mẫu số liệu trên là: 8.

Trung vị của dãy 7; 7; 7; 8 là: $\frac{7+7}{2}=7$ .

Trung vị của dãy 8; 9; 9; 9 là: $\frac{9+9}{2}=9$ .

Vì vậy Q₁ = 7; Q₂ = 8; Q₃ = 9.

Do đó khoảng tứ phân vị của mẫu số liệu (1) là: ∆_Q = Q₃ – Q₁ = 9 – 7 = 2.

Xét mẫu số liệu (2):

⦁ Trong mẫu số liệu (2), số điểm lớn nhất là 10 và số điểm thấp nhất là 6.

Do đó khoảng biến thiên của mẫu số liệu (1) là: R = x_max – x_min = 10 – 6 = 4.

⦁ Sắp xếp mẫu số liệu (2) theo thứ tự không giảm, ta được dãy:

6     6     7     8     8     8     9     9     10

Trung vị của mẫu số liệu trên là: 8.

Trung vị của dãy 6; 6; 7; 8 là: $\frac{6+7}{2}=\mathrm{6,5}$ .

Trung vị của dãy 8; 9; 9; 10 là: $\frac{9+9}{2}=9$ .

Vì vậy Q₁ = 6,5; Q₂ = 8; Q₃ = 9.

Do đó khoảng tứ phân vị của mẫu số liệu (2) là: ∆_Q = Q₃ – Q₁ = 9 – 6,5 = 2,5.

Vậy ta có:

⦁ Khoảng biến thiên của mẫu số liệu (1) và (2) lần lượt là 2 và 4.

⦁ Khoảng tứ phân vị của mẫu số liệu (1) và (2) lần lượt là 2 và 2,5.

c) Gọi kết quả trung bình của bạn Dũng và bạn Hoàng lần lượt là ${\overline{x}}_D,{\overline{x}}_H$ . Ta có:

⦁ ${\overline{x}}_D=\frac{7.3+8.3+9.3}{9}=8$  (điểm).

⦁ ${\overline{x}}_H=\frac{6.2+7+8.3+9.2+10}{9}=\frac{71}{9}$  (điểm).

Gọi phương sai tương ứng với mẫu số liệu (1) và (2) lần lượt là $s_D^2,s_H^2$ . Ta có:

⦁ $s_D^2=\frac{3.{\left(7-8\right)}^2+3.{\left(8-8\right)}^2+3.{\left(9-8\right)}^2}{9}=\frac{2}{3}$ .

⦁ $s_H^2=\frac{2.{\left(6-\frac{71}{9}\right)}^2+{\left(7-\frac{71}{9}\right)}^2+3.{\left(8-\frac{71}{9}\right)}^2+2.{\left(9-\frac{71}{9}\right)}^2+{\left(10-\frac{71}{9}\right)}^2}{9}=\frac{134}{81}$ .

Độ lệch chuẩn của mẫu số liệu (1) là: $s_D=\sqrt{s_D^2}=\sqrt{\frac{2}{3}}=\frac{\sqrt{6}}{3}$ .

Độ lệch chuẩn của mẫu số liệu (2) là: $s_H=\sqrt{s_H^2}=\sqrt{\frac{134}{81}}=\frac{\sqrt{134}}{9}$ .

Do $s_D^2=\frac{2}{3}<s_H^2=\frac{134}{81}$ .

Nên bạn Dũng có kết quả thi ổn định hơn bạn Hoàng.

Xem thêm lời giải sách bài tập Toán lớp 10 Cánh diều hay, chi tiết khác: 

Bài 4: Xác suất của biến cố trong một số trò chơi đơn giản

Bài 5: Xác suất của biến cố

Bài tập cuối chương 6

Bài 1: Tọa độ của vectơ

Bài 2: Biểu thức tọa độ của các phép toán vectơ