Sách bài tập Toán 10 (Cánh diều) Bài ôn tập chương 3

Giải sách bài tập Toán lớp 10 Bài ôn tập chương 3 - Cánh diều

Giải SBT Toán 10 trang 61 Tập 1

Bài 45 trang 61 SBT Toán 10 Tập 1: Trong các hàm số sau, hàm số nào không là hàm số bậc hai?

A. y = – 5x² + 6x;

B. y = 3 – 2x²;

C. y = – x(5x – 7);

D. y = 0x² + 6x – 5.

Lời giải

Đáp án đúng là D

Xét hàm số y = – 5x² + 6x có dạng ax² + bx + c với a = – 5, b = 6 và c = 0. Do đó A sai.

Xét hàm số y = 3 – 2x² = – 2x² + 3 có dạng ax² + bx + c với a = – 2, b = 0 và c = 3. Do đó B sai.

Xét hàm số y = – x(5x – 7) = – 5x² + 7x có dạng ax² + bx + c với a = – 5, b = 7 và c = 0. Do đó C sai.

Xét hàm số y = 0x² + 6x – 5 có dạng ax² + bx + c tuy nhiên a = 0 nên đây không là hàm số bậc hai. Do đó D đúng.

Bài 46 trang 61 SBT Toán 10 Tập 1: Tập nghiệm của bất phương trình – 5x² + 6x + 11 ≤ 0 là:

A. $\left[-1;\frac{11}{5}\right]$;

B. $\left(-1;\frac{11}{5}\right)$;

C. $\left(-\infty ;-1\right)\cup \left(\frac{11}{5};+\infty \right)$;

D. $\left(-\infty ;-1\right]\cup \left[\frac{11}{5};+\infty \right)$.

Lời giải

Đáp án đúng là D

Xét tam thức bậc hai f(x) = – 5x² + 6x + 11 với a = – 5, ∆ = 6² – 4.(– 5).11 = 256 > 0.

Suy ra tam thức f(x) có hai nghiệm phân biệt x₁ = – 1 và x₂ = $\frac{11}{5}$.

Áp dụng định lí về dấu của tam thức bậc hai, ta có: f(x) < 0 khi x ∈ $\left(-\infty ;-1\right)\cup \left(\frac{11}{5};+\infty \right)$.

Do đó bất phương trình – 5x² + 6x + 11 ≤ 0 khi x ∈ $\left(-\infty ;-1\right]\cup \left[\frac{11}{5};+\infty \right)$.

Vậy tập nghiệm của bất phương trình là S = $\left(-\infty ;-1\right]\cup \left[\frac{11}{5};+\infty \right)$.

Giải SBT Toán 10 trang 62 Tập 1

Bài 47 trang 62 SBT Toán 10 Tập 1: Cho hàm số f(x) = $\left\{\begin{array}{l}1khix<0\\ 2khix>0\end{array}\right.$.

a) Điểm nào sau đây thuộc đồ thị hàm số trên:

A(0; 0), B(– 1; 1), C(2 021; 1), D(2 022; 2)?

b) Chỉ ra hai điểm thuộc đồ thị hàm số trên có tung độ bằng 2.

c) Chỉ ra điểm thuộc đồ thị hàm số trên có hoành độ bằng – 2 022.

Lời giải

a) Tập xác định của hàm số đã cho là D = ℝ\{0}.

+) Điểm A(0; 0) có x = 0 không thỏa mãn điều kiện xác định nên không thuộc đồ thị hàm số.

+) Điểm B(– 1; 1) có x = – 1 và y = 1

Vì x = – 1 < 0 nên y = f(x) = 1 (thỏa mãn). Do đó điểm B thuộc đồ thị hàm số đã cho.

+) Điểm C(2 021; 1) có x = 2 021 và y = 1

Vì x = 2 021 > 0 nên y = f(x) = 2 ≠ 1. Do đó điểm C không thuộc đồ thị hàm số đã cho.

+) Điểm D(2 022; 2) có x = 2 022 và y = 2

Vì x = 2 022 > 0 nên y = f(x) = 2 (thỏa mãn). Do đó điểm D thuộc đồ thị hàm số đã cho.

Vậy có điểm B và điểm D thuộc đồ  thị hàm số đã cho.

b) Để điểm có tung độ bằng 2 thì hoành độ của điểm đó phải thỏa mãn x > 0. Do đó ta chọn được được 2 điểm là (100; 2) và (67; 2).

c) Điểm có hoành độ x = – 2 022 < 0 nên tung độ y = 1. Do đó ta có điểm cần tìm là (– 2 022; 1).

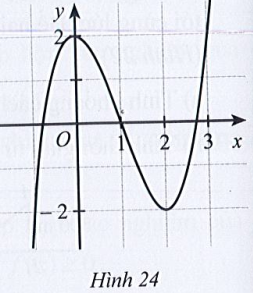
Bài 48 trang 62 SBT Toán 10 Tập 1: Cho hàm số y = f(x) có đồ thị ở Hình 24.

a) Chỉ ra khoảng đồng biến và khoảng nghịch biến của hàm số y = f(x).

b) Nêu tung độ giao điểm của đồ thị hàm số y = f(x) với trục Oy.

Lời giải

a) Dựa vào đồ thị hàm số ta thấy:

Với x < 0 hoặc x > 2 thì đồ thị hàm số đi lên. Do đó hàm số đồng biến trên khoảng (– ∞; 0) ∪ (2; +∞).

Với 0 < x < 2 thì đồ thị hàm số đi xuống. Do đó hàm số nghịch biến trên khoảng (0; 2).

Vậy hàm số đồng biến trên khoảng (– ∞; 0) ∪ (2; +∞) và hàm số nghịch biến trên khoảng (0; 2).

b) Đồ thị hàm số giao với trục tung tại điểm có tung độ bằng 2.

Bài 49 trang 62 SBT Toán 10 Tập 1: Một người vay 100 triệu đồng tại một ngân hàng để mua nhà với lãi suất r%/năm trong thời hạn 2 năm. Hỏi số tiền người này phải trả cho ngân hàng là bao nhiêu triệu đồng sau hai năm?

Lời giải

Sau 1 năm người này nợ ngân hàng số tiền là:

100 + r%.100 = 100.(1 + r%) (triệu đồng).

Sau 2 năm người này phải trả ngân hàng số tiền là:

100.(1 + r%) + r%.100.(1 + r%)  = 100(1 + r%)(1 + r%) = 100(1 + r%)² (triệu đồng).

Vậy sau 2 năm số tiền người này phải trả cho ngân hàng là 100(1 + r%)² (triệu đồng).

Bài 50 trang 62 SBT Toán 10 Tập 1: Vẽ đồ thị của mỗi hàm số sau:

a) y = 2x² – 8x + 1;

b) y = – x² + 4x – 3.

Lời giải

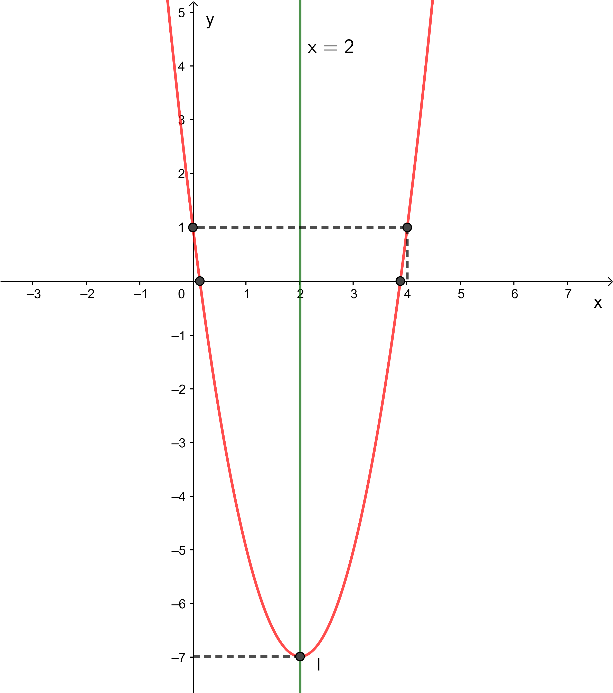
a) Xét hàm số y = 2x² – 8x + 1, có a = 2 > 0, ∆ = (– 8)² – 4.1.2 = 56 > 0.

- Điểm đỉnh: 

$$\begin{gathered} I=\left(-\frac{b}{2a};-\frac{\Delta }{4a}\right) \\ =\left(-\frac{-8}{2.2};-\frac{56}{4.2}\right)=\left(2;-7\right) \end{gathered}$$

- Trục đối xứng là x = 2.

- Vì a = 2 > 0 thì đồ thị hàm số có bề lõm hướng lên trên.

- Đồ thị hàm số cắt trục tung tại điểm có tọa độ (0; 1).

- Điểm đối xứng với điểm (0; 1) qua trục đối xứng là (4; 1).

- Đồ thị cắt trục hoành tại hai điểm có tọa độ $\left(\frac{4-\sqrt{14}}{2};0\right)$ và $\left(\frac{4+\sqrt{14}}{2};0\right)$

Ta có hình vẽ sau:

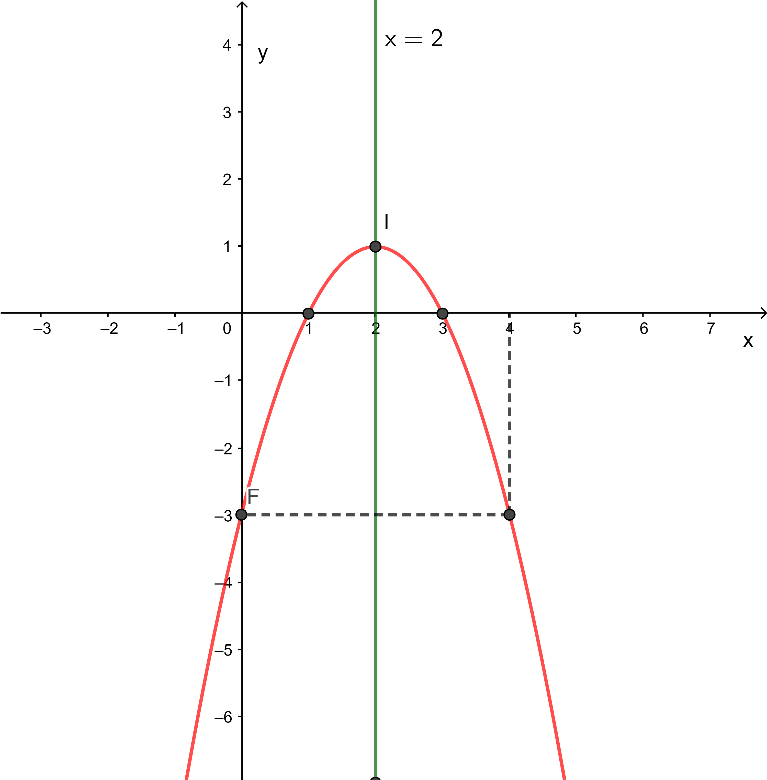
b) Xét hàm số y = – x² + 4x – 3, có a = – 1 < 0, ∆ = 4² – 4.(–1).(–3) = 4 > 0.

- Điểm đỉnh: 

$$\begin{gathered} I=\left(-\frac{b}{2a};-\frac{\Delta }{4a}\right) \\ =\left(-\frac{4}{2.\left(-1\right)};-\frac{4}{4.\left(-1\right)}\right)=\left(2;1\right) \end{gathered}$$

- Trục đối xứng là x = 2.

- Vì a = – 1 < 0 thì đồ thị hàm số có bề lõm hướng xuống dưới.

- Đồ thị hàm số cắt trục tung tại điểm có tọa độ (0; – 3).

- Điểm đối xứng với điểm (0; – 3) qua trục đối xứng là (4; – 3).

- Đồ thị cắt trục hoành tại hai điểm có tọa độ (1; 0) và (3; 0)

Ta có hình vẽ sau:

Bài 51 trang 62 SBT Toán 10 Tập 1: Giải các bất phương trình bậc hai sau:

a) 4x² – 9x + 5 ≤ 0;

b) – 3x² – x + 4 > 0;

c) 36x² – 12x + 1 > 0;

d) – 7x² + 5x + 2 < 0.

Lời giải

a) Xét tam thức bậc hai f(x) = 4x² – 9x + 5, có a = 4 > 0 và ∆ = (– 9)² – 4.4.5 = 1 > 0.

Suy ra tam thức có hai nghiệm x₁ = 1 và x₂ = $\frac{5}{4}$.

Áp dụng định lí về dấu của tam thức bậc hai, ta được:

f(x) < 0 khi x ∈ $\left(1;\frac{5}{4}\right)$.

Suy ra 4x² – 9x + 5 ≤ 0 khi x ∈ $\left[1;\frac{5}{4}\right]$.

Vậy tập nghiệm của bất phương trình S = $\left[1;\frac{5}{4}\right]$.

b) Xét tam thức bậc hai f(x) = – 3x² – x + 4, có a = – 3 < 0 và ∆ = (– 1)² – 4.(– 3).4 = 25 > 0.

Suy ra tam thức có hai nghiệm x₁ = 1 và x₂ = $\frac{-4}{3}$.

Áp dụng định lí về dấu của tam thức bậc hai, ta được:

f(x) > 0 khi x ∈ $\left(-\frac{4}{3};1\right)$.

Suy ra – 3x² – x + 4 > 0 khi x ∈ $\left(-\frac{4}{3};1\right)$.

Vậy tập nghiệm của bất phương trình S = $\left(-\frac{4}{3};1\right)$.

c) Xét tam thức bậc hai f(x) = 36x² – 12x + 1, có a = 36 > 0 và ∆ = (– 12)² – 4.36.1 =

 0.

Suy ra tam thức có nghiệm kép x = $\frac{1}{6}$.

Áp dụng định lí về dấu của tam thức bậc hai, ta được:

f(x) > 0 khi x ≠ $\frac{1}{6}$.

Suy ra 36x² – 12x + 1 > 0 khi x ≠$\frac{1}{6}$.

Vậy tập nghiệm của bất phương trình S = $ℝ\backslash \left\{\frac{1}{6}\right\}$.

d) Xét tam thức bậc hai f(x) = – 7x² + 5x + 2 , có a = – 7 > 0 và ∆ = 5² – 4.(– 7).2 = 81 > 0.

Suy ra tam thức có hai nghiệm x₁ = 1 và x₂ = $-\frac{2}{7}$.

Áp dụng định lí về dấu của tam thức bậc hai, ta được:

f(x) < 0 khi x ∈ $\left(-\infty ;-\frac{2}{7}\right)\cup \left(1;+\infty \right)$.

Suy ra – 7x² + 5x + 2 < 0 khi x ∈ $\left(-\infty ;-\frac{2}{7}\right)\cup \left(1;+\infty \right)$.

Vậy tập nghiệm của bất phương trình S = $\left(-\infty ;-\frac{2}{7}\right)\cup \left(1;+\infty \right)$.

Bài 52 trang 62 SBT Toán 10 Tập 1: Giải các phương trình sau:

a) $\sqrt{8-x}+x=-4$;

b) $\sqrt{3x^2-5x+2}+3x=4$.

Lời giải

a) $\sqrt{8-x}+x=-4$

⇔ $\sqrt{8-x}=-x-4$ (điều kiện – x – 4 ≥ 0 ⇔ x ≤ – 4)

⇔ 8 – x = x² + 8x + 16

⇔ x² + 9x + 8 = 0

⇔ (x + 1)(x + 8) = 0

⇔ x = – 1 (không thỏa mãn) hoặc x = – 8 (thỏa mãn)

Vậy tập nghiệm của phương trình là S = {– 8}.

b) $\sqrt{3x^2-5x+2}+3x=4$

⇔ $\sqrt{3x^2-5x+2}=-3x+4$ (điều kiện – 3x + 4 ≥ 0 ⇔ x ≤ )

⇔ 3x² – 5x + 2 = 9x² – 24x + 16

⇔ 6x² – 19x + 14 = 0

⇔ x = 2 (không thỏa mãn) hoặc x = $\frac{7}{6}$ (thỏa mãn)

Vậy tập nghiệm của phương trình là S = $\left\{\frac{7}{6}\right\}$.

Bài 53 trang 62 SBT Toán 10 Tập 1: Hình 25 cho biết bảng giá cước của một hãng taxi (đã bao gồm thuế VAT):

a) Số tiền phải trả y (đồng) có phải hàm số của quãng đường x (km) khi đi taxi hay không? Giải thích. Nếu đúng, hãy xác định những công thức tính y theo x biểu thị cho trong bảng trên.

b) Quãng đường x (km) có phải là hàm số của số tiền phải trả y (đồng) không? Giải thích.

c) Tính số tiền bạn Quân phải trả khi đi taxi hãng trên với quãng đường 20km.

Lời giải

a) Dựa vào bảng ta có số ứng với mỗi quãng đường x ta sẽ xác định được duy nhất một giá trị của y. Do đó số tiền phải trả y (đồng) có phải hàm số của quãng đường x (km).

Dựa vào bảng trên, ta có công thức tính y theo x là:

$y=\left\{\begin{array}{l}5000khi0<x\le 0,3\\ 20600khi0,3<x\le 2\\ 16000khi2<x\le 10\\ 17600khi10<x\le 25\\ 15100khix>25\end{array}\right.$.

b) Ta thấy với giá trị y = 5 000 đồng ta xác định được rất nhiều giá trị của x thỏa mãn 0 < x ≤ 0,3. Do đó x không phải là hàm số của y.

c) Ta có x = 20 thỏa mãn 10 < x ≤ 25.

Khi đó theo công thức xác định của hàm số y theo x ta có y = 17 600.

Số tiền bạn Quân phải trả khi đi taxi hãng trên với quãng đường 20 km là:

17 600.20 = 352 000 (đồng)

Vậy Quân phải trả 352 000 đồng cho hãng taxi trên.

Giải SBT Toán 10 trang 63 Tập 1

Bài 54 trang 63 SBT Toán 10 Tập 1: Quan sát chiếc Cổng Vàng (Golden Gate bridge) ở Hình 26. Độ cao h (feet) tính từ mặt cầu đến các điểm trên dây treo ở phần giữa hai trụ cầu được xác định bởi công thức h(x) = $\frac{1}{9000}{x}^2-\frac{7}{15}x+500$, trong đó x(feet) là khoảng cách từ trụ cầu bên trái đến điểm tương ứng trên dây treo.

a) Xác định độ cao của trụ cầu so với mặt cầu theo đơn vị feet.

b) Xác định khoảng cách giữa hai trụ cầu theo đơn vị feet, biết rằng hai trụ cầu này có độ cao bằng nhau.

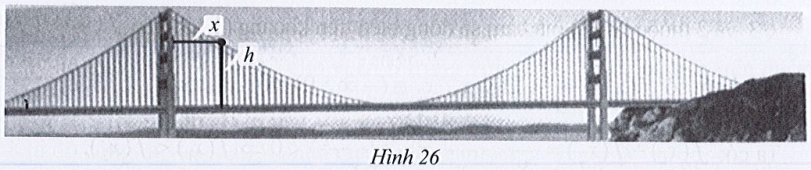
Lời giải

Đặt hệ trục như hình vẽ dưới đây:

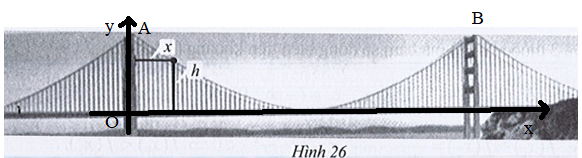
a) Độ cao của trụ cầu bên trái chính là tung độ của điểm giao giữa trụ cầu (trục tung) và dây treo (parabol) là điểm A.

Thay x = 0 vào h(x) = $\frac{1}{9000}{x}^2-\frac{7}{15}x+500$, ta được h(0) = $\frac{1}{9000}{.0}^2-\frac{7}{15}.0+500$ = 500.

Vậy chiều cao của trụ cầu bên trái là 500 (feet).

b) Trụ cầu bên phải có chiều cao bằng trụ cầu bên trái và bằng 500m. Do đó tung độ điểm B là y_B = 500.

Vì B cũng thuộc vào parabol nên thay y_B = 500 vào h(x) = $\frac{1}{9000}{x}^2-\frac{7}{15}x+500$, ta được:

500 = $\frac{1}{9000}{x}^2-\frac{7}{15}x+500$

⇔ x = 0 hoặc x = 4200.

Vì x_B > 0 nên x_B = 4200.

Vậy khoảng cách giữa hai trụ cầu là 4200 (feet).

Bài 55 trang 63 SBT Toán 10 Tập 1: Bác Nam dự định làm một khung ảnh hình chữ nhật sao cho phần trong của khung là hình chữ nhật có kích thước 6cm x 11cm, độ rộng viền xung quanh là x cm (Hình 27). Diện tích của viền khung ảnh không vượt quá 38 cm². Hỏi độ rộng viền khung ảnh lớn nhất là bao nhiêu xăng – ti – mét?

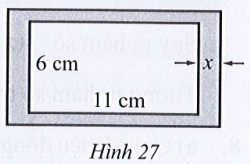
Lời giải

Đặt hình chữ nhật ABCD là phần trong của khung, hình chữ nhật MNPQ là khung ảnh hình chữ nhật như hình vẽ:

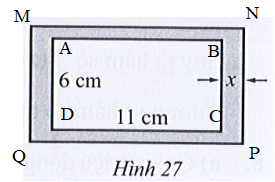
Chiều dài hình chữ nhật MNPQ là: x + 11 + x = 2x + 11 (cm).

Chiều rộng hình chữ nhật MNPQ là: x + 6 + x = 2x + 6 (cm).

Diện tích hình chữ nhật MNPQ là: (2x + 11)(2x + 6) = 4x² + 34x + 66 (cm²).

Diện tích của hình chữ nhật ABCD là: 6.11 = 66 (cm²).

Diện tích của viền khung ảnh là: 4x² + 34x + 66 – 66 = 4x² + 34x (cm²).

Vì diện tích của viền khung ảnh không vượt quá 38 cm² nên ta có:

4x² + 34x ≤ 38 ⇔ 4x² + 34x – 38 ≤ 0

Xét tam thức f(x) = 4x² + 34x – 38, có a = 4 > 0 và ∆ = 34² – 4.4.(– 38) = 1 764 > 0.

Suy ra tam thức f(x) có hai nghiệm phân biệt x₁ = 1 và x₂ = $-\frac{19}{2}$.

Áp dụng định lí về dấu của tam thức bậc hai, ta có: f(x) < 0 khi x ∈ $\left(-\frac{19}{2};1\right)$.

Do đó bất phương trình 4x² + 34x – 38 ≤ 0 khi x ∈ $\left[-\frac{19}{2};1\right]$.

Mà x > 0 nên ta có 0 < x ≤ 1 thì thỏa mãn 4x² + 34x – 38 ≤ 0.

Vậy độ rộng viền khung ảnh lớn nhất là 1 xăng – ti – mét.

Bài 56 trang 63 SBT Toán 10 Tập 1: Hai địa điểm A và B cách nhau bởi một con sông (coi hai bờ sông song song). Người ta muốn xây một chiếc cầu bắc vuông góc với bờ sông để có thể đi từ A đến B. Với các số liệu (tính theo đơn vị ki – lô – mét) cho trên Hình 28, tìm x(km) để xác định vị trí đặt chân cầu sao cho khoảng cách từ B đến chân cầu phía B gấp đôi khoảng cách từ A đến chân cầu phía A.

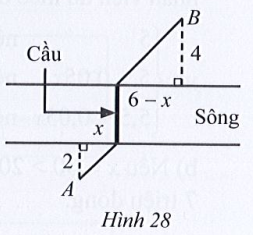
Lời giải

Đặt tọa độ các điểm như hình vẽ:

Ta có AD = x nên x > 0

Xét tam giác BHC vuông tại H, có:

BC² = BH² + CH² (định lí py – ta – go)

BC² = 4² + (6 – x)²

BC² = 16 + 36 – 12x + x²

BC² = x² – 12x + 52

BC = $\sqrt{x^2-12x+52}$

Xét tam giác AKD vuông tại K, có:

AD² = AK² + KD² (định lí py – ta – go)

AD² = 2² + x²

AD² = x² + 4

AD = $\sqrt{x^2+4}$

Để vị trí đặt chân cầu sao cho khoảng cách từ B đến chân cầu phía B gấp đôi khoảng cách từ A đến chân cầu phía A ta có BC = 2AD

Hay $\sqrt{x^2-12x+52}=2\sqrt{x^2+4}$

Điều kiện x² + 4 ≥ 0 luôn đúng với mọi x.

⇔ x² – 12x + 52 = 4(x² + 4)

⇔ x² – 12x + 52 = 4x² + 16

⇔ 3x² + 12x –  36 = 0

⇔ x = 2 (thỏa mãn) hoặc x = – 6 (không thỏa mãn)

Vậy x = 2 thỏa mãn yêu cầu bài toán.

Xem thêm lời giải sách bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

Bài 1: Hàm số và đồ thị

Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng

Bài 3: Dấu của tam thức bậc hai

Bài 4: Bất phương trình bậc nhất một ẩn

Bài 5: Hai dạng phương trình quy về phương trình bậc hai

Xem thêm tài liệu Toán lớp 10 Cánh diều hay, chi tiết khác:

Lý thuyết Bài tập cuối chương 3