Nội dung bài viết

    Xem thêm

    Vẽ đồ thị của mỗi hàm số sau

    Lời giải Bài 50 trang 62 SBT Toán 10 Tập 1 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10.

    1 277 05/12/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 10 Cánh diều Bài ôn tập chương 3

    Bài 50 trang 62 SBT Toán 10 Tập 1: Vẽ đồ thị của mỗi hàm số sau:

    a) y = 2x2 – 8x + 1;

    b) y = – x2 + 4x – 3.

    Lời giải

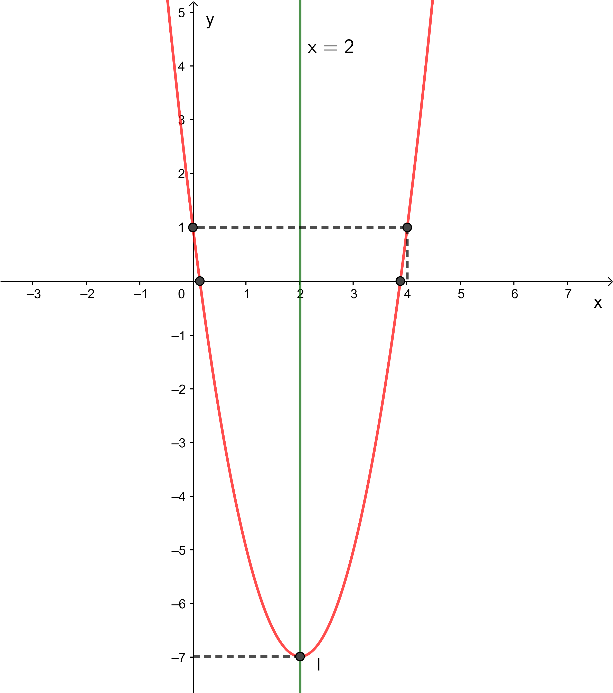
    a) Xét hàm số y = 2x2 – 8x + 1, có a = 2 > 0, ∆ = (– 8)2 – 4.1.2 = 56 > 0.

    - Điểm đỉnh: 

    I=−b2a;−Δ4a=−−82.2;−564.2=2;−7

    - Trục đối xứng là x = 2.

    - Vì a = 2 > 0 thì đồ thị hàm số có bề lõm hướng lên trên.

    - Đồ thị hàm số cắt trục tung tại điểm có tọa độ (0; 1).

    - Điểm đối xứng với điểm (0; 1) qua trục đối xứng là (4; 1).

    - Đồ thị cắt trục hoành tại hai điểm có tọa độ 4−142;0 và 4+142;0

    Ta có hình vẽ sau:

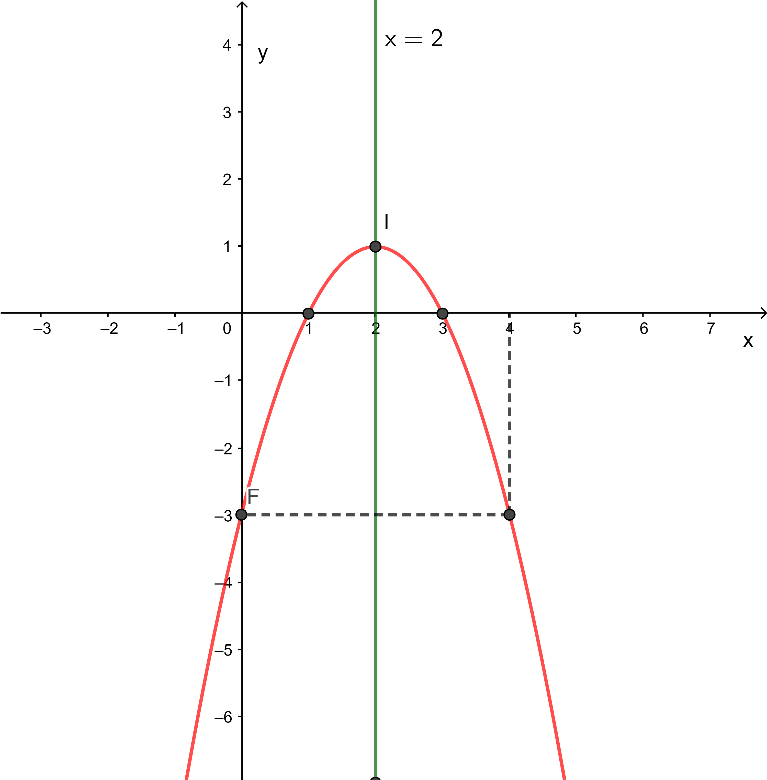
    Sách bài tập Toán 10 Bài ôn tập chương 3 - Cánh diều (ảnh 1)

    b) Xét hàm số y = – x2 + 4x – 3, có a = – 1 < 0, ∆ = 42 – 4.(–1).(–3) = 4 > 0.

    - Điểm đỉnh: 

    I=−b2a;−Δ4a=−42.−1;−44.−1=2;1

    - Trục đối xứng là x = 2.

    - Vì a = – 1 < 0 thì đồ thị hàm số có bề lõm hướng xuống dưới.

    - Đồ thị hàm số cắt trục tung tại điểm có tọa độ (0; – 3).

    - Điểm đối xứng với điểm (0; – 3) qua trục đối xứng là (4; – 3).

    - Đồ thị cắt trục hoành tại hai điểm có tọa độ (1; 0) và (3; 0)

    Ta có hình vẽ sau:

    Sách bài tập Toán 10 Bài ôn tập chương 3 - Cánh diều (ảnh 1)

    Xem thêm các bài giải sách giáo khoa Toán 10 bộ sách Cánh diều hay, chi tiết khác:

    Bài 45 trang 61 SBT Toán 10 Tập 1: Trong các hàm số sau, hàm số nào không là hàm số bậc hai?...

    Bài 46 trang 61 SBT Toán 10 Tập 1: Tập nghiệm của bất phương trình – 5x2 + 6x + 11 ≤ 0 là:...

    Bài 47 trang 62 SBT Toán 10 Tập 1: Cho hàm số f(x) =...

    Bài 48 trang 62 SBT Toán 10 Tập 1: Cho hàm số y = f(x) có đồ thị ở Hình 24....

    Bài 49 trang 62 SBT Toán 10 Tập 1: Một người vay 100 triệu đồng tại một ngân hàng để mua...

    Bài 50 trang 62 SBT Toán 10 Tập 1: Vẽ đồ thị của mỗi hàm số sau:...

    Bài 51 trang 62 SBT Toán 10 Tập 1: Giải các bất phương trình bậc hai sau:...

    Bài 52 trang 62 SBT Toán 10 Tập 1: Giải các phương trình sau:...

    Bài 53 trang 62 SBT Toán 10 Tập 1: Hình 25 cho biết bảng giá cước của một hãng taxi (đã bao gồm thuế VAT):...

    Bài 54 trang 63 SBT Toán 10 Tập 1: Quan sát chiếc Cổng Vàng (Golden Gate bridge) ở Hình...

    Bài 55 trang 63 SBT Toán 10 Tập 1: Bác Nam dự định làm một khung ảnh hình chữ nhật sao...

    Bài 56 trang 63 SBT Toán 10 Tập 1: Hai địa điểm A và B cách nhau bởi một con sông (coi hai...

    Xem thêm lời giải sách bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

    Bài 1: Hàm số và đồ thị

    Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng

    Bài 3: Dấu của tam thức bậc hai

    Bài 4: Bất phương trình bậc nhất một ẩn

    Bài 5: Hai dạng phương trình quy về phương trình bậc hai

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 277 05/12/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: