Sách bài tập Toán 10 Bài 1 (Cánh diều): Quy tắc cộng. Quy tắc nhân. Sơ đồ hình cây

Giải sách bài tập Toán lớp 10 Bài 1: Quy tắc cộng. Quy tắc nhân. Sơ đồ hình cây - Cánh diều

Giải SBT Toán 10 trang 5 Tập 2

Bài 1 trang 5 SBT Toán 10 Tập 2:

Một công việc được hoàn thành bởi một trong ba hành động. Nếu hành động thứ nhất có a cách thực hiện, hành động thứ hai có b cách thực hiện, hành động thứ ba có c cách thực hiện (các cách thực hiện của ba hành động là khác nhau đôi một) thì số cách hoàn thành công việc đó là:

A. abc.

B. a + b + c.

C. 1.

D. ab + c.

Lời giải:

Đáp án đúng là B

Một công việc được hoàn thành bởi một trong ba hành động. Nếu hành động thứ nhất có a cách thực hiện, hành động thứ hai có b cách thực hiện, hành động thứ ba có c cách thực hiện (các cách thực hiện của ba hành động là khác nhau đôi một) thì công việc đó có a + b + c cách hoàn thành.

Vậy ta chọn phương án B.

Bài 2 trang 5 SBT Toán 10 Tập 2:

Một công việc được hoàn thành bởi ba hành động liên tiếp. Nếu hành động thứ nhất có a cách thực hiện; ứng với mỗi cách thực hiện hành động thứ nhất, có b cách thực hiện hành động thứ hai; ứng với mỗi cách thực hiện hành động thứ nhất và mỗi cách thực hiện hành động thứ hai có c cách thực hiện hành động thứ ba thì số cách hoàn thành công việc đó là:

A. abc.

B. a + b + c.

C. 1.

D. ab + c.

Lời giải:

Đáp án đúng là A

Một công việc được hoàn thành bởi ba hành động liên tiếp. Nếu hành động thứ nhất có a cách thực hiện; ứng với mỗi cách thực hiện hành động thứ nhất, có b cách thực hiện hành động thứ hai; ứng với mỗi cách thực hiện hành động thứ nhất và mỗi cách thực hiện hành động thứ hai có c cách thực hiện hành động thứ ba thì công việc đó có a.b.c cách hoàn thành.

Vậy ta chọn phương án A.

Giải SBT Toán 10 trang 6 Tập 2

Bài 3 trang 6 SBT Toán 10 Tập 2:

Lớp 10A có 10 bạn nữ và 25 bạn nam. Có bao nhiêu cách chọn một bạn để làm lớp trưởng?

Lời giải:

Tổng số học sinh lớp 10A là: 10 + 25 = 35 (học sinh).

Nếu chọn một học sinh trong số 35 học sinh lớp 10A để làm lớp trưởng thì có 35 cách chọn.

Vậy có 35 cách chọn một bạn làm lớp trưởng lớp 10A.

Bài 4 trang 6 SBT Toán 10 Tập 2:

Bạn Nam có 8 quyển sách Toán, 6 quyển sách Vật lí và 5 quyển sách Hóa học, các quyển sách là khác nhau. Hỏi bạn Nam có bao nhiêu cách chọn một quyển sách để đọc?

Lời giải:

Tổng số quyển sách bạn Nam có là: 8 + 6 + 5 = 19 (quyển sách).

Nếu chọn một quyển sách trong số 19 quyển sách thì có 19 cách chọn.

Vậy bạn Nam có 19 cách chọn một quyển sách để đọc.

Bài 5 trang 6 SBT Toán 10 Tập 2:

Cho 20 điểm phân biệt. Hỏi lập được bao nhiêu vectơ khác ? Biết rằng hai đầu mút của mỗi vectơ là 2 trong 20 điểm đã cho.

Lời giải:

Việc chọn hai điểm phân biệt trong số 20 điểm phân biệt để lập thành một vectơ là thực hiện hai hành động liên tiếp: chọn một điểm đầu tiên, sau đó chọn một điểm còn lại.

Có 20 cách chọn một điểm đầu tiên trong số 20 điểm phân biệt.

Vì ta đã chọn một điểm trên nên bây giờ ta chỉ còn 19 điểm phân biệt. Vì vậy lúc này có 19 cách chọn một điểm còn lại.

Vậy ta có thể lập được tất cả 20.19 = 380 vectơ khác $\overrightarrow{0}$  từ 20 điểm đã cho.

Bài 6 trang 6 SBT Toán 10 Tập 2:

Bạn Quân dự định đặt mật khẩu cho vali của mình bằng dãy có 3 kí tự là các chữ số. Hỏi có bao nhiêu cách để Quân có thể đặt một mật khẩu cho vali?

Lời giải:

Ta thấy các chữ số của mỗi kí tự bạn Quân có thể lựa chọn là các số 0; 1; 2; 3; 4; 5; 6; 7; 8; 9. Tức là có tổng cộng 10 số cho bạn Quân lựa chọn.

Việc chọn 3 kí tự cho dãy mật khẩu là thực hiện ba hành động liên tiếp: chọn số cho kí tự đầu tiên, sau đó chọn số cho kí tự thứ hai, cuối cùng là chọn số cho kí tự thứ ba.

Ở kí tự đầu tiên, bạn Quân có 10 cách chọn một số từ các số trên.

Tương tự như vậy, ở kí tự thứ hai, bạn Quân cũng có 10 cách chọn một số từ các số trên và ở kí tự thứ ba, bạn Quân cũng có 10 cách chọn một số từ các số trên.

Vậy bạn Quân có tất cả 10.10.10 = 10³ = 1000 cách chọn dãy mật khẩu cho vali.

Bài 7 trang 6 SBT Toán 10 Tập 2:

Lớp 10A có 30 học sinh. Giáo viên chủ nhiệm muốn chọn ban cán sự lớp gồm 3 thành viên: 1 lớp trưởng, 1 lớp phó học tập, 1 lớp phó văn thể. Hỏi giáo viên có bao nhiêu cách chọn một ban cán sự lớp?

Lời giải:

Việc chọn một ban cán sự lớp gồm 1 lớp trưởng, 1 lớp phó học tập và 1 lớp phó văn thể là thực hiện ba hành động liên tiếp: chọn 1 lớp trưởng, sau đó chọn 1 lớp phó học tập và cuối cùng chọn 1 lớp phó văn thể.

Vì lớp 10A có tất cả 30 học sinh nên có 30 cách chọn một lớp trưởng.

Vì giáo viên đã chọn một học sinh làm lớp trưởng nên lúc này ta có 29 cách chọn một lớp phó học tập.

Vì giáo viên đã chọn một học sinh làm lớp trưởng và một lớp phó học tập nên lúc này ta có 28 cách chọn một lớp phó văn thể.

Vậy giáo viên có tất cả 30.29.28 = 24360 cách chọn một ban cán sự lớp.

Bài 8 trang 6 SBT Toán 10 Tập 2:

Trong loạt đá luân lưu giữa hai đội tuyển, huấn luyện viên của một đội phải lập danh sách 5 cầu thủ từ 11 cầu thủ trên sân và xếp thứ tự đá luân lưu của họ. Hỏi huấn luyện viên có bao nhiêu cách lập một danh sách cầu thủ đá luân lưu? Biết ông sẽ để đội trưởng là người sút lượt thứ nhất và tiền đạo cắm (không phải đội trưởng) là người sút lượt thứ ba.

Lời giải:

Vì đội trưởng là người sút lượt thứ nhất và tiền đạo cắm là người sút lượt thứ ba nên chỉ còn 3 lượt sút thứ hai, thứ tư và thứ năm cần sắp xếp.

Sau khi xếp lượt sút của đội trưởng và tiền đạo cắm thì còn 9 cầu thủ để huấn luyện viên lựa chọn.

Việc chọn 3 cầu thủ trong số 9 cầu thủ và xếp thứ tự đá luân lưu của họ là thực hiện 3 hành động liên tiếp: chọn cầu thủ sút lượt thứ hai, sau đó chọn cầu thủ sút lượt thứ tư và cuối cùng là chọn cầu thủ sút lượt thứ năm.

Huấn luyện viên có 9 cách chọn một cầu thủ sút lượt thứ hai.

Vì huấn luyện viên đã chọn một cầu thủ sút lượt thứ hai, nên lúc này ông có 8 cách chọn một cầu thủ sút lượt thứ tư.

Vì huấn luyện viên đã chọn hai cầu thủ sút lượt thứ hai và thứ tư, nên lúc này ông có 7 cách chọn một cầu thủ sút lượt thứ năm.

Vậy huấn luyện viên có tất cả 9.8.7 = 504 cách lập một danh sách 5 cầu thủ đá luân lưu.

Bài 9 trang 6 SBT Toán 10 Tập 2:

Có 10 cặp vợ chồng dự tiệc. Tính số cách chọn ra một nam và một nữ trong bữa tiệc để phát biểu ý kiến, sao cho:

a) Hai người đó là một cặp vợ chồng;

b) Hai người đó không là vợ chồng.

Lời giải:

a) Vì có 10 cặp vợ chồng dự tiệc nên ta có 10 nam và 10 nữ.

Việc chọn một cặp vợ chồng để phát biểu ý kiến là thực hiện hai hành động liên tiếp: đầu tiên chọn 1 nam, sau đó chọn 1 nữ là vợ của người nam đã chọn.

Chọn 1 nam có 10 cách chọn.

Chọn 1 nữ là vợ của người nam đã chọn chỉ có 1 cách chọn.

Vậy có tất cả 10.1 = 10 cách chọn hai người trong bữa tiệc để phát biểu ý kiến sao cho hai người đó là một cặp vợ chồng.

b) Việc chọn một cặp vợ chồng để phát biểu ý kiến là thực hiện hai hành động liên tiếp: đầu tiên chọn 1 nam, sau đó chọn 1 nữ không phải là vợ của người nam đã chọn.

Chọn 1 nam có 10 cách chọn.

Chọn 1 nữ không phải là vợ của người nam đã chọn thì có 9 cách chọn.

Vậy có tất cả 10.9 = 90 cách chọn hai người trong bữa tiệc để phát biểu ý kiến sao cho hai người đó không phải là vợ chồng.

Bài 10 trang 6 SBT Toán 10 Tập 2:

Cho kiểu gen AaBBDdEe. Giả sử quá trình giảm phân tạo giao tử bình thường, không xảy ra đột biến.

a) Vẽ sơ đồ hình cây biểu thị sự hình thành giao tử.

b) Từ đó, tính số loại giao tử của kiểu gen AaBBDdEe.

Lời giải:

a) Sơ đồ hình cây biểu thị sự hình thành giao tử:

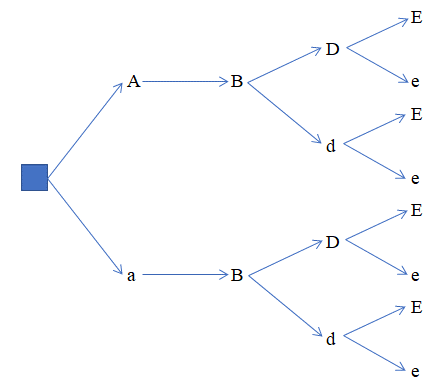
 b) Từ sơ đồ cây, ta có 8 loại giao tử của kiểu gen AaBBDdEe là: ABDE, ABDe, ABdE, ABde, aBDE, aBDe, aBdE, aBde.

Xem thêm lời giải sách bài tập Toán lớp 10 Cánh diều với cuộc sống hay, chi tiết khác: 

Bài ôn tập chương 4

Bài 2: Hoán vị. Chỉnh hợp

Bài 3: Tổ hợp

Bài 4: Nhị thức Newton

Bài tập cuối chương V