Nội dung bài viết

    Xem thêm

    Giải SBT Toán 10 trang 56 Tập 1 Cánh diều

    Với Giải SBT Toán 10 trang 56 Tập 1 trong Bài 4: Bất phương trình bậc nhất một ẩn Toán lớp 10 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 10 trang 56.

    1 269 23/09/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 10 trang 56 Tập 1 Cánh diều

    Bài 28 trang 56 SBT Toán 10 Tập 1: Trong các bất phương tình sau, bất phương trình nào không là bất phương trình bậc nhất một ẩn?

    A.  – 2x2 + 3x < 0;

    B. 0,5y2 – 3(y – 2) ≤ 0;

    C. x2 – 2xy – 3 ≥ 0;

    D. 2x2 – 3 ≥ 0.

    Lời giải

    Đáp án đúng là C

    Xét bất phương trình  – 2x2 + 3x < 0 là bất phương trình bậc hai một ẩn x. Do đó A sai.

    Xét bất phương trình 0,5y2 – 3(y – 2) ≤ 0 ⇔ 0,5y2 – 3y + 23 ≤ 0 là bất phương trình bậc hai một ẩn y. Do đó B sai.

    Xét bất phương trình x2 – 2xy – 3 ≥ 0 là bất phương trình bậc hai nhưng lại có hai ẩn x và y. Do đó C đúng.

    Xét bất phương trình 2x2 – 3 ≥ 0 là bất phương trình bậc hai một ẩn x. Do đó D sai.

    Bài 29 trang 56 SBT Toán 10 Tập 1: Tập nghiệm của bất phương trình  – x2 + 3x + 18 ≥ 0 là:

    A. [ – 3; 6];

    B. (– 3; 6);

    C. (– ∞; – 3) ∪ (6; +∞);

    D. (– ∞; – 3] ∪ [6; +∞).

    Lời giải

    Đáp án đúng là A

    Xét f(x) = – x2 + 3x + 18 là một tam thức bậc hai có a = – 1 < 0 và ∆ = 32 – 4.(– 1).18 = 81 > 0.

    Do đó f(x) có hai nghiệm phân biệt là x1 = – 3 và x2 = 6.

    Theo định lí về dấu tam thức bậc hai, ta có:

    f(x) > 0 khi x ∈ (– 3; 6);

    f(x) < 0 khi x ∈ (–∞; – 3) ∪ (6; +∞);

    Suy ra f(x) ≥ 0 khi x ∈ [– 3; 6].

    Vậy tập nghiệm của bất phương trình là S = [– 3; 6].

    Bài 30 trang 56 SBT Toán 10 Tập 1: Dựa vào đồ thị hàm số bậc hai y = f(x) trong mỗi Hình 18a, 18b, 18c, hãy viết tập nghiệm các bất phương trình sau: f(x) > 0; f(x) < 0; f(x) ≥ 0 và f(x) ≤ 0.

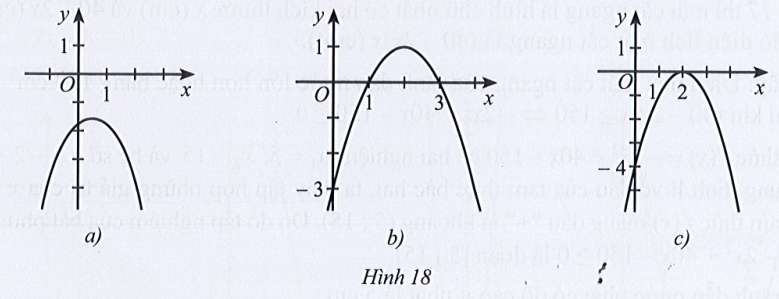
    Sách bài tập Toán 10 Bài 4: Bất phương trình bậc nhất một ẩn - Cánh diều (ảnh 1)

    Lời giải

    +) Hình 18a):

    Quan sát đồ thị hàm số, ta thấy:

    Đồ thị hàm số nằm hoàn toàn phía dưới trục hoành với mọi x ∈ ℝ.

    Do đó:

    f(x) < 0 và f(x) ≤ 0 luôn đúng với mọi x ∈ ℝ.

    f(x) > 0; f(x) ≥ 0 và vô nghiệm.

    Vậy tập nghiệm của các bất phương trình f(x) > 0 và f(x) ≥ 0 là ∅, tập nghiệm của bất phương trình f(x) < 0 và f(x) ≤ 0 là ℝ.

    +) Hình 18b):

    Quan sát đồ thị hàm số, ta thấy:

    Với x ∈ (1; 3) hàm số nằm trên trục hoành hay f(x) > 0.

    Với x < 1 hoặc x > 3 đồ thị hàm số nằm phía dưới trục hoành hay f(x) < 0.

    Đồ thị hàm số cắt trục hoành tại x = 1 hoặc x = 3.

    Do đó:

    f(x) > 0 khi x ∈ (1; 3).

    f(x) < 0 khi x ∈ (– ∞; 1) ∪ (3; +∞).

    f(x) ≥ 0 khi x ∈ [1; 3].

    f(x) ≤ 0 khi x ∈ (– ∞; 1] ∪ [3; +∞).

    Vậy tập nghiệm của các bất phương trình f(x) > 0; f(x) < 0; f(x) ≥ 0; f(x) ≤ 0 lần lượt là (1; 3); (– ∞; 1) ∪ (3; +∞); [1; 3]; (– ∞; 1] ∪ [3; +∞).

    +) Hình 18c):

    Quan sát đồ thị hàm số, ta thấy:

    Đồ thị hàm số cắt trục hoành tại x = 2.

    Với x ≠ 2 hàm số nằm dưới trục hoành hay f(x) < 0.

    Do đó:

    f(x) > 0 vô nghiệm.

    f(x) < 0 khi x ∈ ℝ \ {2}.

    f(x) ≥ 0 khi x = 2.

    f(x) ≤ 0 khi x ∈ ℝ.

    Vậy tập nghiệm của các bất phương trình f(x) > 0; f(x) < 0; f(x) ≥ 0; f(x) ≤ 0 lần lượt là ∅; ℝ \ {2}; {2}; ℝ.

    Bài 31 trang 56 SBT Toán 10 Tập 1: Giải các bất phương trình bậc hai sau:

    a) 3x2 – 8x + 5 > 0;

    b) – 2x2 – x + 3 ≤ 0;

    c) 25x2 – 10x + 1 < 0;

    d) – 4x2 + 5x + 9 ≥ 0.

    Lời giải

    a) Xét tam thức bậc hai f(x) = 3x2 – 8x + 5, có a = 3, ∆ = (– 8)2 – 4.3.5 = 4 > 0

    Suy ra tam thức bậc hai có hai nghiệm x1 = 1 và x2 =53.

    Áp dụng định lí dấu của tam thức bậc hai, ta có:

    f(x) > 0 khi x ∈ −∞;1∪53;+∞;

    f(x) < 0 khi x ∈ 1;53.

    Suy ra 3x2 – 8x + 5 > 0 khi x ∈ −∞;1∪53;+∞.

    Vậy tập nghiệm của bất phương trình 3x2 – 8x + 5 > 0 là −∞;1∪53;+∞.

    b) Xét tam thức bậc hai g(x) =  – 2x2 – x + 3, có a = – 2 < 0 và ∆ = (– 1)2 – 4.(– 2).3 = 25 > 0.

    Do đó tam thức có hai nghiệm phân biệt x1 = 1 và x2 =-32.

    Áp dụng định lí về dấu của tam thức bậc hai ta có:

    g(x) > 0 khi x ∈ −32;1;

    g(x) < 0 khi x ∈ −∞;−32∪1;+∞.

    Suy ra  – 2x2 – x + 3 ≤ 0 khi x ∈ −∞;−32∪1;+∞.

    Vậy tập nghiệm của bất phương trình đã cho là S = −∞;−32∪1;+∞.

    c) Xét tam thức bậc hai h(x) =  25x2 – 10x + 1, có a = 25 > 0 và ∆ = (– 10)2 – 4.25.1 = 0.

    Do đó tam thức có nghiệm kép là x = 15.

    Áp dụng định lí về dấu của tam thức bậc hai ta có:

    h(x) > 0 khi x ≠ 15.

    Suy ra  25x2 – 10x + 1 < 0 khi x ∈ ∅.

    Vậy tập nghiệm của bất phương trình đã cho là S = ∅.

    d) Xét tam thức bậc hai k(x) =  – 4x2 + 5x + 9 , có a = – 4 < 0 và ∆ = 52 – 4.(– 4).9 = 169 > 0.

    Do đó tam thức có hai nghiệm phân biệt là x1 = – 1 và x2 = 94.

    Áp dụng định lí về dấu của tam thức bậc hai ta có:

    k(x) < 0 khi x ∈ −∞;−1∪94;+∞;

    k(x) > 0 khi x ∈ −1;94.

    Suy ra – 4x2 + 5x + 9 ≥ 0 khi x ∈ −1;94.

    Vậy tập nghiệm của bất phương trình đã cho là S = −1;94.

    Xem thêm lời giải sách bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

    Giải SBT Toán 10 trang 57 Tập 1

    Xem thêm các bài giải sách giáo khoa Toán 10 bộ sách Cánh diều hay, chi tiết khác:

    Bài 28 trang 56 SBT Toán 10 Tập 1: Trong các bất phương tình sau, bất phương trình nào...

    Bài 29 trang 56 SBT Toán 10 Tập 1: Tập nghiệm của bất phương trình  – x2 + 3x + 18 ≥ 0 là:...

    Bài 30 trang 56 SBT Toán 10 Tập 1: Dựa vào đồ thị hàm số bậc hai y = f(x) trong mỗi Hình...

    Bài 31 trang 56 SBT Toán 10 Tập 1: Giải các bất phương trình bậc hai sau:...

    Bài 32 trang 57 SBT Toán 10 Tập 1: Tìm giao các tập nghiệm của hai bất phương trình – 3x2 +...

    Bài 33 trang 57 SBT Toán 10 Tập 1: Tìm m để phương trình – x2 + (m + 2)x + 2m – 10 = 0 có...

    Bài 34 trang 57 SBT Toán 10 Tập 1: Xét hệ tọa độ Oth trong mặt phẳng, trong đó trục Ot biể...

    Bài 35 trang 57 SBT Toán 10 Tập 1: Một tình huống trong huấn luyện pháo binh được mô tả...

    Xem thêm lời giải sách bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

    Bài ôn tập chương 2

    Bài 1: Hàm số và đồ thị

    Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng

    Bài 3: Dấu của tam thức bậc hai

    Bài 5: Hai dạng phương trình quy về phương trình bậc hai

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 269 23/09/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: