Nội dung bài viết

    Xem thêm

    Cho tam giác ABC có AB = 5, BC = 6, CA = 7. Tính

    Lời giải Bài 74 trang 107 SBT Toán 10 Tập 1 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10.

    1 1,169 05/12/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 10 Cánh diều Bài ôn tập chương 4

    Bài 74 trang 107 SBT Toán 10 Tập 1: Cho tam giác ABC có AB = 5, BC = 6, CA = 7. Tính:

    a) sinABC^;

    b) Diện tích tam giác ABC;

    c) Độ dài đường trung tuyến AM.

    Lời giải:

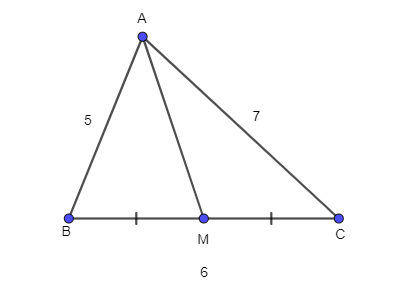
    Sách bài tập Toán 10 Bài ôn tập chương 4 - Cánh diều (ảnh 1)

    a) Xét tam giác ABC, có:

    Áp dụng hệ quả của định lí cosin, ta được:

    cosABC^=AB2+BC2−AC22AB.BC=52+62−722.5.6=15

    Ta có: cos2ABC^+sin2ABC^=1

    ⇔ sin2ABC^=1−cos2ABC^=1−152=2425

    Vì ABC^ là góc trong tam giác nên 0°<ABC^<180°

    ⇒ sinABC^=265.

    Vậy sinABC^=265.

    b) Diện tích tam giác ABC là:

    SΔABC=12AB.BC.sinABC^=12.5.6.265=66đvdt

    Vậy diện tích tam giác ABC là 66

    c) Vì M là trung điểm của BC nên BM = MC = 12BC = 12.6 = 3.

    Xét tam giác ABM:

    Áp dụng định lí cos, ta có:

    AM2 = AB2 + BM2 – 2.AM.BM.cosB

    ⇔ AM2 = 52 + 32 – 2.5.3.

    ⇔ AM2 = 28

    ⇔ AM = 27

    Vậy độ dài đường trung tuyến AM là 27.

    Xem thêm các bài giải sách giáo khoa Toán 10 bộ sách Cánh diều hay, chi tiết khác:

    Bài 67 trang 106 SBT Toán 10 Tập 1: Cho góc nhọn α. Biểu thức (sinα . cotα)2 + (cosα . tanα)2...

    Bài 68 trang 106 SBT Toán 10 Tập 1: Cho các vectơ a→,b→≠0→. Phát biểu nào sau đây là đúng?...

    Bài 69 trang 106 SBT Toán 10 Tập 1: Cho tứ giác ABCD. Biểu thức...

    Bài 70 trang 106 SBT Toán 10 Tập 1: Cho góc nhọn α. Biểu thức tanα . tan(90°– α) bằng:...

    Bài 71 trang 106 SBT Toán 10 Tập 1: Cho α thỏa mãn...

    Bài 72 trang 107 SBT Toán 10 Tập 1: Cho tam giác ABC có AB = 4, AC = 6...

    Bài 73 trang 107 SBT Toán 10 Tập 1: Cho tam giác ABC. Chứng minh rằng...

    Bài 74 trang 107 SBT Toán 10 Tập 1: Cho tam giác ABC có AB = 5, BC = 6, CA = 7. Tính:...

    Bài 75 trang 107 SBT Toán 10 Tập 1: Cho ba điểm I, A, B và số thực k ≠ 1 thỏa mã...

    Bài 76 trang 107 SBT Toán 10 Tập 1: Cho tam giác ABC có AB = 4, AC = 5...

    Bài 77 trang 107 SBT Toán 10 Tập 1: Một người quan sát đứng ở bờ sông muốn đo độ rộng của...

    Bài 78 trang 107 SBT Toán 10 Tập 1: Cho hai vectơ...

    Bài 79 trang 108 SBT Toán 10 Tập 1: a) Chứng minh đẳng thức...

    Bài 80 trang 108 SBT Toán 10 Tập 1: Cho tam giác ABC, có ba trung tuyến AD, BE, CF...

    Bài 81 trang 108 SBT Toán 10 Tập 1: Cho tứ giác ABCD, M là điểm thay đổi trong mặt phẳng...

    Bài 82 trang 108 SBT Toán 10 Tập 1: Cho tam giác ABC và đường thẳng d không có điểm...

    Xem thêm lời giải sách bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

    Bài 2: Giải tam giác. Tính diện tích tam giác

    Bài 3: Khái niệm vectơ

    Bài 4: Tổng và hiệu của hai vectơ

    Bài 5: Tích của một số với một vectơ

    Bài 6: Tích vô hướng của hai vectơ

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,169 05/12/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: