Nội dung bài viết

    Xem thêm

    Giải Toán 7 trang 32 Tập 2 Kết nối tri thức

    Với giải bài tập Toán lớp 7 trang 32 Tập 2 trong Bài 26: Phép cộng và phép trừ đa thức một biến sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 7 trang 32 Tập 2.

    1 235 07/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 7 trang 32 Tập 2

    Câu hỏi trang 32 Toán 7 Tập 2:

    Tìm tổng của hai đa thức: x3 - 5x + 2 và x3 - x2 + 6x - 4.

    Lời giải:

    Ta có:

    (x3 - 5x + 2) + (x3 - x2 + 6x - 4)

    = x3 - 5x + 2 + x3 - x2 + 6x - 4

    = (x3 + x3) - x2 + (- 5x + 6x) + (2 - 4)

    = 2x3 - x2 + x + (-2)

    = 2x3 - x2 + x - 2.

    Luyện tập 1 trang 32 Toán 7 Tập 2:

    Cho hai đa thức M = 0,5x4 - 4x3 + 2x - 2,5 và N = 2x3 + x2 + 1,5.

    Hãy tính tổng M + N (trình bày theo hai cách).

    Lời giải:

    Cách 1. Đặt tính cộng:

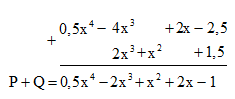
    Giải Toán 7 Bài 26 (Kết nối tri thức): Phép cộng và phép trừ đa thức một biến (ảnh 1)

    Cách 2. Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc:

    M + N = (0,5x4 – 4x3 + 2x – 2,5) + (2x3 + x2 + 1,5)

               = 0,5x4 – 4x3 + 2x – 2,5 + 2x3 + x2 + 1,5

               = 0,5x4 + (– 4x3 + 2x3) + x2 + 2x + (– 2,5 + 1,5)

               = 0,5x4 + (– 2x3) + x2 + 2x + (–1)

               = 0,5x4 – 2x3 + x2 + 2x – 1.

    Vậy M + N = 0,5x4 - 2x3 + x2 + 2x - 1.

    Vận dụng 1 trang 32 Toán 7 Tập 2:

    Đặt tính cộng để tìm tổng của ba đa thức sau:

    A = 2x3 - 5x2 + x - 7;

    B = x2 - 2x + 6;

    C = -x3 + 4x2 - 1.

    Lời giải:

    Ta có: A + B + C = (A + B) + C

    Đặt tính A + B như sau:

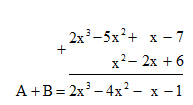
    Giải Toán 7 Bài 26 (Kết nối tri thức): Phép cộng và phép trừ đa thức một biến (ảnh 1)

    Đặt tính (A + B) + C như sau:

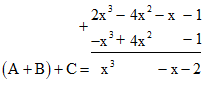
    Giải Toán 7 Bài 26 (Kết nối tri thức): Phép cộng và phép trừ đa thức một biến (ảnh 1)

    Vậy A + B + C = x3 - x - 2.

    Hoạt động 1 trang 32 Toán 7 Tập 2:

    Cho hai đa thức P = x4 + 3x3 - 5x2 + 7x và Q = -x3 + 4x2 - 2x + 1.

    Đối với phép trừ: P - Q = (x4 + 3x3 - 5x2 + 7x) - (-x3 + 4x2 - 2x + 1), ta cũng có hai cách trình bày, tương tự như phép cộng hai đa thức.

    Tìm hiệu P - Q bằng cách bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc và thu gọn.

    Lời giải:

    P – Q = (x4 + 3x3 – 5x2 + 7x) – (–x3 + 4x2 – 2x + 1)

              = x4 + 3x3 – 5x2 + 7x + x3 – 4x2 + 2x – 1

              = x4 + (3x3 + x3) + (– 5x2 – 4x2) + (7x + 2x) – 1

              = x4 + 4x3 + (– 9x2) + 9x – 1

              = x4+ 4x3 – 9x2 + 9x – 1.

    Vậy P – Q = x4 + 4x3 – 9x2 + 9x – 1.

    Hoạt động 2 trang 32 Toán 7 Tập 2:

    Cho hai đa thức P = x4 + 3x3 - 5x2 + 7x và Q = -x3 + 4x2 - 2x + 1.

    Đối với phép trừ: P - Q = (x4 + 3x3 - 5x2 + 7x) - (-x3 + 4x2 - 2x + 1), ta cũng có hai cách trình bày, tương tự như phép cộng hai đa thức.

    Tìm hiệu P - Q bằng cách đặt tính trừ: đặt đa thức Q dưới đa thức P sao cho các hạng tử cùng bậc thẳng cột với nhau rồi trừ theo từng cột.

    Lời giải:

    Đặt tính trừ P - Q như sau:

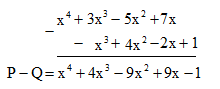
    Giải Toán 7 Bài 26 (Kết nối tri thức): Phép cộng và phép trừ đa thức một biến (ảnh 1)

    Vậy P – Q = x4 + 4x3 – 9x2 + 9x – 1.

    Luyện tập 2 trang 32 Toán 7 Tập 2:

    Cho hai đa thức:

    M = 0,5x4 - 4x3 + 2x - 2,5 và N = 2x3 + x2 + 1,5.

    Hãy tính hiệu M - N (trình bày theo hai cách).

    Lời giải:

    Cách 1. Đặt tính trừ:

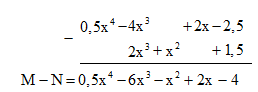
    Giải Toán 7 Bài 26 (Kết nối tri thức): Phép cộng và phép trừ đa thức một biến (ảnh 1)

    Cách 2. Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc và thu gọn.

    M - N = (0,5x4 - 4x3 + 2x - 2,5) - (2x3 + x2 + 1,5)

               = 0,5x4 - 4x3 + 2x - 2,5 - 2x3 - x2 - 1,5

               = 0,5x4 + (-4x3 - 2x3) - x2 + 2x + (-2,5 - 1,5)

               = 0,5x4 + (-6x3) - x2 + 2x + (-4)

               = 0,5x4 - 6x3 - x2 + 2x - 4

    Vậy M - N = 0,5x4 - 6x3 - x2 + 2x - 4.

    Xem thêm các bài giải sách giáo khoa Toán 7 bộ sách Kết nối tri thức hay, chi tiết khác:

    Giải Toán 7 trang 32 Tập 2

    Giải Toán 7 trang 33 Tập 2

    Xem thêm các bài giải sách giáo khoa Toán 7 bộ sách Kết nối tri thức hay, chi tiết khác:

    Luyện tập chung trang 35

    Bài 27: Phép nhân đa thức một biến

    Bài 28: Phép chia đa thức một biến

    Luyện tập chung trang 45

    Bài tập cuối chương 7

    Tham khảo các loạt bài Toán 7 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 235 07/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: