Trên đường tròn lượng giác, xác định điểm M biểu diễn các góc lượng giác có số đo

Lời giải Bài 1.51 trang 28 SBT Toán 11 Tập 1 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11.

1 1,700 17/11/2024

Trang trước

Trang sau

Giải SBT Toán 11 Bài tập cuối chương 1 trang 25

Bài 1.51 trang 28 SBT Toán 11 Tập 1: Trên đường tròn lượng giác, xác định điểm M biểu diễn các góc lượng giác có số đo sau và tính các giá trị lượng giác của chúng.

a) $\frac{23 π}{4}$ ; b) $\frac{31 π}{6}$ ; c) – 1 380°.

*Lời giải:

a) Ta có $\frac{23 π}{4} = 6 π - \frac{π}{4}$ . Góc $\frac{23 π}{4}$ được biểu diễn bởi điểm $M (\frac{\sqrt{2}}{2}; - \frac{\sqrt{2}}{2})$ trên đường tròn lượng giác (hình dưới).

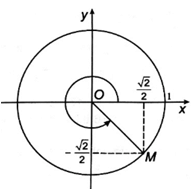
Trên đường tròn lượng giác xác định điểm M biểu diễn các góc lượng giác có số đo sau

Vậy $\sin \frac{23 π}{4} = - \frac{\sqrt{2}}{2}; \cos \frac{23 π}{4} = \frac{\sqrt{2}}{2}$ và $\tan \frac{23 π}{4} = \cot \frac{23 π}{4} = - 1$ .

b) Ta có $\frac{31 π}{6} = \frac{7 π}{6} + 4 π$ . Góс $\frac{31 π}{6}$ được biểu diễn bởi điểm $M (- \frac{\sqrt{3}}{2}; - \frac{1}{2})$ > trên đường tròn lượng giác (hình dưới).

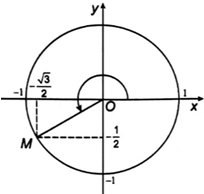
Trên đường tròn lượng giác xác định điểm M biểu diễn các góc lượng giác có số đo sau

Vậy $\sin \frac{31 π}{6} = - \frac{1}{2}; \cos \frac{31 π}{6} = - \frac{\sqrt{3}}{2}$ ; $\tan \frac{31 π}{6} = \frac{1}{\sqrt{3}}$ và $\cot \frac{31 π}{6} = \sqrt{3}$ .

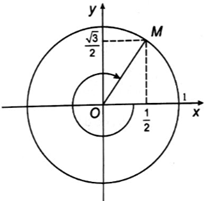
c) Ta có – 1 380° = − 4 . 360° + 60°. Góc –1 380° được biểu diễn bởi điểm $M (\frac{1}{2}; \frac{\sqrt{3}}{2})$ trên đường tròn lượng giác (hình dưới).

Trên đường tròn lượng giác xác định điểm M biểu diễn các góc lượng giác có số đo sau

Vậy sin(– 1 380°) = $\frac{\sqrt{3}}{2}$ ; cos(– 1 380°) = $\frac{1}{2}$ ; tan(– 1 380°) = $\sqrt{3}$ và cot(– 1 380°) = $\frac{1}{\sqrt{3}}$ .

*Phương pháp giải

- Sử dụng các góc lượng giác đặc biệt. Biến đổi các giá trị đề bài cho, rồi vẽ trên đường tròn lượng giác

* Lý thuyết cần nắm và một số dạng toán về hàm số lượng giác:

- Quy tắc đặt tương ứng mỗi số thực x với số thực sinx được gọi là hàm số sin, kí hiệu y = sinx. Tập xác định của hàm số sin là $R$ .

- Quy tắc đặt tương ứng mỗi số thực x với số thực cosx được gọi là hàm số cos, kí hiệu y = cosx. Tập xác định của hàm số côsin là $R$ .

- Hàm số cho bằng công thức $y = \frac{\sin α}{\cos α}$ được gọi là hàm số tang, kí hiệu là y = tanx. Tập xác định của hàm số tang là $R ∖ {\frac{π}{2} + k π | k \in Z}$ .

- Hàm số cho bằng công thức $y = \frac{\cos α}{\sin α}$ được gọi là hàm số tang, kí hiệu là y = tanx. Tập xác định của hàm số tang là $R ∖ {k π | k \in Z}$ .

Hàm số tuần hoàn

Hàm số y = f(x) có tập xác định D được gọi là hàm số tuần hoàn nếu tồn tại số T $\neq$ 0 sao cho với mọi $x \in D$ ta có:

+) $x + T \in D$ và $x - T \in D$

+) $f (x + T) = f (x)$

Số T dương nhỏ nhất thỏa mãn cách điều kiện trên (nêu có) được gọi là chu kì của hàm số tuần hoàn đó.

* Nhận xét:

Các hàm số y = sinx, y=cosx tuần hoàn chu kì 2 $π$ .

Các hàm số y = tanx, y=cotx tuần hoàn chu kì $π$ .

Đồ thị và tính chất của hàm số y = sinx

- Tập xác định là $R$ .

- Tập giá trị là [-1;1].

- Là hàm số lẻ và tuần hoàn chu kì 2 $π$ .

- Đồng biến trên mỗi khoảng $(- \frac{π}{2} + k 2 π; \frac{π}{2} + k 2 π)$ và nghịch biến trên mỗi khoảng $(\frac{π}{2} + k 2 π; \frac{3 π}{2} + k 2 π)$ .