Sách bài tập Toán 11 (Kết nối tri thức) Bài tập cuối chương 6 trang 20

Giải SBT Toán 11 Bài tập cuối chương 6 trang 20

Bài 6.41 trang 20 SBT Toán 11 Tập 2: Cho a là số dương. Rút gọn biểu thức $A=\frac{\sqrt{a}\cdot \sqrt[3]{a^2}}{\sqrt[6]{a}}$ , ta được kết quả là

A. a.

B. a².

C. $a^{\frac{1}{3}}$.

D. $a^{\frac{1}{2}}$.

Lời giải:

Đáp án đúng là: A

Ta có: $A=\frac{\sqrt{a}\cdot \sqrt[3]{a^2}}{\sqrt[6]{a}}=\frac{a^{\frac{1}{2}}\cdot a^{\frac{2}{3}}}{a^{\frac{1}{6}}}=\frac{a^{\frac{1}{2}+\frac{2}{3}}}{a^{\frac{1}{6}}}=\frac{a^{\frac{7}{6}}}{a^{\frac{1}{6}}}=a^{\frac{7}{6}-\frac{1}{6}}=a$ .

Bài 6.42 trang 20 SBT Toán 11 Tập 2: Cho a là số dương khác 1. Giá trị của ${\log }_{a^3}{a}^2$ là

A. $\frac{2}{3}$.

B. $\frac{3}{2}$.

C. $-\frac{2}{3}$.

D. $-\frac{3}{2}$.

Lời giải:

Đáp án đúng là: A

Ta có: ${\log }_{a^3}{a}^2=\frac{1}{3}{\log }_a{a}^2=\frac{1}{3}\cdot 2{\log }_{a}a=\frac{2}{3}$

Bài 6.43 trang 20 SBT Toán 11 Tập 2: Giá trị của biểu thức $4^{{\log }_{\sqrt{2}}3}$ là

A. $\frac{1}{3}$.

B. 3.

C. 81.

D. 9.

Lời giải:

Đáp án đúng là: C

Ta có: $4^{{\log }_{\sqrt{2}}3}=2^{2{\log }_{\sqrt{2}}3}=2^{2\cdot 2{\log }_{2}3}={\left(2^{{\log }_{2}3}\right)}^4=3^4=81.$

Bài 6.44 trang 21 SBT Toán 11 Tập 2: Trong các hàm số sau, hàm số nào đồng biến?

A. $y={\left(\frac{\sqrt{3}}{2}\right)}^x$ .

B. $y={\left(\frac{e}{3}\right)}^x$ .

C. $y={\left(\frac{\pi }{2}\right)}^x$ .

D. $y={\left(\frac{3}{\pi }\right)}^x$ .

Lời giải:

Đáp án đúng là: C

Vì $\frac{\pi }{2}>1$ nên hàm số $y={\left(\frac{\pi }{2}\right)}^x$ là hàm số đồng biến.

Bài 6.45 trang 21 SBT Toán 11 Tập 2: Trong các hàm số sau, hàm số nào nghịch biến?

A. $y={\log }_{\sqrt{2}}x$ .

B. y = log x.

C. y = ln x.

D. $y={\log }_{\frac{e}{3}}x$ .

Lời giải:

Đáp án đúng là: D

Vì $0<\frac{e}{3}<1$ nên hàm số $y={\log }_{\frac{e}{3}}x$ là hàm số nghịch biến.

Bài 6.46 trang 21 SBT Toán 11 Tập 2: Với giá trị nào của x thì đồ thị hàm số $y={\left(\frac{2}{3}\right)}^x$ nằm phía trên đường thẳng y = 1?

A. x > 0.

B. x < 0.

C. x > 1.

D. x < 1.

Lời giải:

Đáp án đúng là: B

Để đồ thị hàm số $y={\left(\frac{2}{3}\right)}^x$ nằm phía trên đường thẳng y = 1 thì

${\left(\frac{2}{3}\right)}^x>1\iff {\left(\frac{2}{3}\right)}^x>{\left(\frac{2}{3}\right)}^0\iff x<0.$

Bài 6.47 trang 21 SBT Toán 11 Tập 2: Với giá trị nào của x thì đồ thị hàm số y = log_0,5 x nằm phía trên trục hoành?

A. x > 0,5.

B. x < 0,5.

C. x > 1.

D. x < 1.

Lời giải:

Để đồ thị hàm số y = log_0,5 x nằm phía trên trục hoành thì

log_0,5 x > 0 $\iff$ log_0,5 x > log_0,51 $\iff$ x < 1.

Bài 6.48 trang 21 SBT Toán 11 Tập 2: Tập nghiệm của phương trình $8^{2x-1}={\left(\frac{1}{4}\right)}^x$là

A. $\left\{\frac{3}{8}\right\}$ .

B. $\left\{\frac{2}{5}\right\}$.

C. $\left\{\frac{3}{4}\right\}$.

D. $\left\{\frac{2}{3}\right\}$.

Lời giải:

Đáp án đúng là: A

Ta có:

$$\begin{gathered} 8^{2x-1}={\left(\frac{1}{4}\right)}^x\iff 8^{2x-1}=4^{-x} \\ \iff 2^{3\left(2x-1\right)}=2^{-2x} \\ \iff 3\left(2x-1\right)=-2x \end{gathered}$$

$\iff 6x-3=-2x\iff 8x=3\iff x=\frac{3}{8}$.

Vậy tập nghiệm của phương trình là $S=\left\{\frac{3}{8}\right\}$

Bài 6.49 trang 21 SBT Toán 11 Tập 2: Tập nghiệm của phương trình log₂ [x(x – 1)] = 1 là

A. {−1}.

B. {−2}.

C. {−1; 2}.

D. $\left\{\frac{-1-\sqrt{5}}{2};\frac{-1+\sqrt{5}}{2}\right\}$.

Lời giải:

Đáp án đúng là: C

Điều kiện: x(x – 1) > 0 $\iff \left[\begin{array}{l}\mathrm{x}<0\\ \mathrm{x}>1\end{array}\right.$.

Ta có: log₂ [x(x – 1)] = log₂ 2

$\iff$ x(x – 1) = 2 $\iff$ x² – x – 2 = 0

$\iff$ (x – 2)(x + 1) = 0 $\iff$ x = 2 (tm) hoặc x = −1 (tm).

Vậy tập nghiệm của phương trình là S = {−1; 2}.

Bài 6.50 trang 21 SBT Toán 11 Tập 2: Nghiệm của bất phương trình ${\left(\frac{1}{2}\right)}^x\ge {\left(\frac{1}{4}\right)}^2$ là

A. x ≥ 2.

B. x ≤ 2.

C. x ≥ 4.

D. x ≤ 4.

Lời giải:

Đáp án đúng là: D

Ta có: ${\left(\frac{1}{2}\right)}^x\ge {\left(\frac{1}{4}\right)}^2\iff {\left(\frac{1}{2}\right)}^x\ge {\left(\frac{1}{2}\right)}^4\iff x\le 4$ .

Vậy nghiệm của bất phương trình là x ≤ 4.

Bài 6.51 trang 21 SBT Toán 11 Tập 2: Nghiệm của bất phương trình log 2(x + 1) > 1 là

A. x > 4.

B. −1 < x < 4.

C. $x>-\frac{1}{2}$ .

D. $x>\frac{e}{2}-1$ .

Lời giải:

Đáp án đúng là: A

Điều kiện: 2(x + 1) > 0 $\iff$ x > – 1.

Ta có: log 2(x + 1) > 1 $\iff$ log 2(x + 1) > log 10

$\iff$ 2(x + 1) > 10 $\iff$ 2x + 2 > 10 $\iff$ 2x > 8 $\iff$ x > 4.

Vậy nghiệm của bất phương trình là x > 4.

Bài 6.52 trang 21 SBT Toán 11 Tập 2: Hàm số y = ln (x² – 2mx + 1) có tập xác định là ℝ khi

A. m = 1.

B. m > 1 hoặc m < −1.

C. m < 1.

D. −1 < m < 1.

Lời giải:

Đáp án đúng là: D

Điều kiện: x² – 2mx + 1 > 0.

Hàm số y = ln (x² – 2mx + 1) có tập xác định là ℝ khi x² – 2mx + 1 > 0 với mọi x ∈ ℝ

$$\begin{gathered} \iff \left\{\begin{array}{l}a=1>0\\ {\Delta }^{\text{'}}=m^2-1<0\end{array}\right.\iff \left\{\begin{array}{l}a=1>0\\ \left(m-1\right)\left(m+1\right)<0\end{array}\right. \\ \iff -1<m<1 \end{gathered}$$

Vậy tập xác định của hàm số đã cho là ℝ khi −1 < m < 1

Bài 6.53 trang 22 SBT Toán 11 Tập 2: Tính giá trị của biểu thức:

$A=2{\log }_{4}8-3{\log }_{\frac{1}{8}}16+4^{{\log }_{2}3}$.

Lời giải:

Ta có$A=2{\log }_{4}8-3{\log }_{\frac{1}{8}}16+4^{{\log }_{2}3}$

$$\begin{gathered} =2{\log }_{2^2}{2}^3-3{\log }_{2^{-3}}{2}^4+2^{2{\log }_{2}3} \\ =2\cdot \frac{1}{2}{\log }_2{2}^3-3\cdot \frac{-1}{3}{\log }_2{2}^4+{\left(2^{{\log }_{2}3}\right)}^2 \\ ={\log }_2{2}^3+{\log }_2{2}^4+3^2 \\ =3{\log }_{2}2+4{\log }_{2}2+3^2=3+4+9=16. \end{gathered}$$

Vậy A = 16.

Bài 6.54 trang 22 SBT Toán 11 Tập 2: Giải các phương trình sau:

a) ${32}^{\frac{x+5}{x-7}}=0,25\cdot {128}^{\frac{x+17}{x-3}}$;

b) log₂ x + log₂ (x – 1) = 1.

Lời giải:

a) Điều kiện:$\left\{\begin{array}{l}\mathrm{x}-7\ne 0\\ \mathrm{x}-3\ne 0\end{array}\right.\iff \left\{\begin{array}{l}\mathrm{x}\ne 7\\ \mathrm{x}\ne 3\end{array}\right.$

Ta có:

${32}^{\frac{x+5}{x-7}}=0,25\cdot {128}^{\frac{x+17}{x-3}}$

$\iff 2^{5\cdot \frac{x+5}{x-7}}=2^{-2}\cdot 2^{7\cdot \frac{x+17}{x-3}}$

$\iff 2^{\frac{5\left(x+5\right)}{x-7}}=2^{-2+\frac{7\left(x+17\right)}{x-3}}$

$\iff \frac{5\left(x+5\right)}{x-7}=-2+\frac{7\left(x+17\right)}{x-3}$

$\iff \frac{5\left(x+5\right)\left(x-3\right)}{\left(x-7\right)\left(x-3\right)}=\frac{-2\left(x-7\right)\left(x-3\right)}{\left(x-7\right)\left(x-3\right)}+\frac{7\left(x+17\right)\left(x-7\right)}{\left(x-7\right)\left(x-3\right)}$

$\Rightarrow 5\left(x+5\right)\left(x-3\right)=-2\left(x-7\right)\left(x-3\right)+7\left(x+17\right)\left(x-7\right)$

$\iff 5\left(x^2+2x-15\right)=-2\left(x^2-10x+21\right)+7\left(x^2+10x-119\right)$

$\iff 5x^2+10x-75=-2x^2+20x-42+7x^2+70x-833$

$\iff 5x^2+10x-75=5x^2+90x-875$

$\iff 80x=800\iff x=10$ (thỏa mãn điều kiện).

Vậy nghiệm của phương trình là x = 10.

b) Điều kiện: $\left\{\begin{array}{l}\mathrm{x}>0\\ \mathrm{x}-1>0\end{array}\right.\iff \left\{\begin{array}{l}\mathrm{x}>0\\ \mathrm{x}>1\end{array}\right.\iff \mathrm{x}>1$.

Ta có: log₂ x + log₂ (x – 1) = 1 $\iff$ log₂ [x(x – 1)] = log₂ 2

$\iff$ x(x – 1) = 2 $\iff$ x² – x – 2 = 0

$\iff$ (x + 1)(x – 2) = 0 $\iff$ x = −1 (loại) hoặc x = 2 (thỏa mãn điều kiện).

Vậy nghiệm của phương trình là x = 2.

Bài 6.55 trang 22 SBT Toán 11 Tập 2: Giải các bất phương trình sau:

a) ${\left(\frac{1}{2}\right)}^{3x-1}\ge 4\cdot 2^x$ ;

b) 2log (x – 1) > log (3 – x) + 1.

Lời giải:

a) Ta có: ${\left(\frac{1}{2}\right)}^{3x-1}\ge 4\cdot 2^x$

$\iff 2^{-\left(3x-1\right)}\ge 2^2\cdot 2^x$$\iff 2^{-\left(3x-1\right)}\ge 2^{2+x}$

$\iff -\left(3x-1\right)\ge 2+x$$\iff 1-3x\ge 2+x$

$\iff 4x\le -1$$\iff x\le -\frac{1}{4}$.

Vậy tập nghiệm của bất phương trình là $\left(-\mathrm{\infty };-\frac{1}{4}\right]$.

b) Điều kiện: $\left\{\begin{array}{l}\mathrm{x}-1>0\\ 3-\mathrm{x}>0\end{array}\right.$$\iff \left\{\begin{array}{l}\mathrm{x}>1\\ \mathrm{x}<3\end{array}\right.$$\iff 1<\mathrm{x}<3$.

Ta có: 2log (x – 1) > log (3 – x) + 1

$\iff$ log (x – 1)² > log (3 – x) + log 10

$\iff$log (x – 1)² > log 10(3 – x)

$\iff$ (x – 1)² > 10(3 – x)

$\iff$ x² – 2x + 1 – 30 + 10x > 0

$\iff$ x² + 8x – 29 > 0 $\iff \left[\begin{array}{l}\mathrm{x}>-4+3\sqrt{5}\\ \mathrm{x}<-4-3\sqrt{5}\end{array}\right.$.

Kết hợp điều kiện, ta có $-4+3\sqrt{5}<x<3$ .

Vậy tập nghiệm của bất phương trình là $\left(-4+3\sqrt{5};3\right)$ .

Bài 6.56 trang 22 SBT Toán 11 Tập 2:

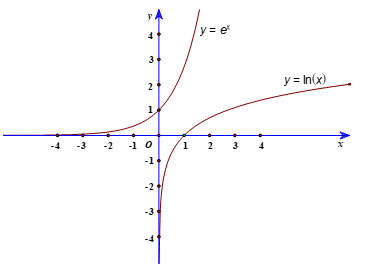
a) Vẽ đồ thị của hai hàm số y = e^x và y = ln x trên cùng một hệ trục tọa độ.

b) Chứng minh rằng hai đồ thị trên đối xứng nhau qua đường thẳng y = x, tức là nếu điểm M nằm trên một đồ thị thì điểm M’ đối xứng với M qua đường thẳng y = x sẽ nằm trên đồ thị còn lại.

Lời giải:

a) Đồ thị của hai hàm số y = e^x và y = ln x trên cùng một hệ trục tọa độ như hình sau:

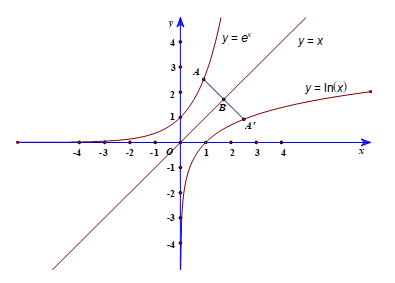
b) Xét điểm $A\left(x_0;e^{x_0}\right)$ nằm trên đồ thị hàm số y = e^x.

Phương trình đường thẳng (d) đi qua điểm $A\left(x_0;e^{x_0}\right)$ và vuông góc với đường thẳng y = x có dạng: $y=-x+x_0+e^{x_0}$ .

Gọi B là giao điểm của đường thẳng (d) và đường thẳng y = x.

Khi đó $B\left(\frac{x_0+e^{x_0}}{2};\frac{x_0+e^{x_0}}{2}\right)$ .

Gọi A’ là điểm đối xứng với A qua đường thẳng y = x. Khi đó B là trung điểm của AA’.

Do đó: $\left\{\begin{array}{l}{\mathrm{x}}_{{\mathrm{A}}^{\text{'}}}=2{\mathrm{x}}_{\mathrm{B}}-{\mathrm{x}}_{\mathrm{A}}\\ {\mathrm{y}}_{{\mathrm{A}}^{\text{'}}}=2{\mathrm{y}}_{\mathrm{B}}-{\mathrm{y}}_{\mathrm{A}}\end{array}\right.$$\iff \left\{\begin{array}{l}{\mathrm{x}}_{{}_{{\mathrm{A}}^{\text{'}}}}=2\cdot \frac{{\mathrm{x}}_0+{\mathrm{e}}^{{\mathrm{x}}_0}}{2}-{\mathrm{x}}_0\\ {\mathrm{y}}_{{}_{{\mathrm{A}}^{\text{'}}}}=2\cdot \frac{{\mathrm{x}}_0+{\mathrm{e}}^{{\mathrm{x}}_0}}{2}-{\mathrm{e}}^{{\mathrm{x}}_0}\end{array}\right.$$\iff \left\{\begin{array}{l}{\mathrm{x}}_{{\mathrm{A}}^{\text{'}}}={\mathrm{e}}^{{\mathrm{x}}_0}\\ {\mathrm{y}}_{{\mathrm{A}}^{\text{'}}}={\mathrm{x}}_0\end{array}\right.$.Vậy ${\mathrm{A}}^{\text{'}}\left({\mathrm{e}}^{{\mathrm{x}}_0};{\mathrm{x}}_0\right)$

Thay tọa độ điểm $A^{\text{'}}\left(e^{x_0};x_0\right)$ vào hàm số y = ln x, ta được $x_0={\mathrm{lne}}^{x_0}$ (luôn đúng),

Vậy $A^{\text{'}}\left(e^{x_0};x_0\right)$ thuộc đồ thị hàm số y = ln x.

Tương tự, nếu B(x₀; ln x₀) nằm trên đồ thị hàm số y = ln x thì ta cũng tìm được điểm B’ đối xứng với B qua đường thẳng y = x và điểm B’ thuộc đồ thị hàm số y = e^x.

Vậy hai đồ thị đã cho đối xứng với nhau qua đường thẳng y = x.

Bài 6.57 trang 22 SBT Toán 11 Tập 2: Cho hàm số f(x) = log₃ (2x + 1) – 2.

a) Tìm tập xác định của hàm số.

b) Tính f(40). Xác định điểm tương ứng trên đồ thị hàm số.

c) Tìm x sao cho f(x) = 3. Xác định điểm tương ứng trên đồ thị hàm số.

d) Tìm giao điểm của đồ thị với trục hoành.

Lời giải:

a) Điều kiện: 2x + 1 > 0 $\iff x>-\frac{1}{2}$ .

Tập xác định của hàm số là $\left(-\frac{1}{2};+\infty \right)$ .

b) Có f(40) = log₃ (2×40 + 1) – 2 = log₃ 81 – 2 = log₃ 3⁴ – 2 = 4 – 2 = 2.

Điểm tương ứng trên đồ thị là (40; 2).

c) Có f(x) = 3 $\iff$ log₃ (2x + 1) – 2 = 3

$\iff$ log₃ (2x + 1) = 5 $\iff$ 2x + 1 = 3⁵

$\iff$ 2x = 242 $\iff$ x = 121.

Điểm tương ứng trên đồ thị là (121; 3).

d) Gọi A(x₀; 0) là giao điểm của đồ thị hàm số f(x) = log₃ (2x + 1) – 2 với trục hoành.

Ta có log₃ (2x₀ + 1) – 2 = 0 $\iff$ log₃ (2x₀ + 1) = 2 $\iff$ 2x₀ + 1 = 3² $\iff$ 2x₀ = 8 $\iff$ x₀ = 4.

Vậy giao điểm cần tìm là (4; 0).

Bài 6.58 trang 22 SBT Toán 11 Tập 2: Nếu tỉ lệ lạm phát trung bình hằng năm là 4% thì chi phí C cho việc mua một loại hàng hóa hoặc sử dụng một dịch vụ nào đó sẽ được mô hình hóa bằng công thức:

C(t) = P(1 + 0,04)^t,

trong đó t là thời gian (tính bằng năm) kể từ thời điểm hiện tại và P là chi phí hiện tại cho hàng hóa hoặc dịch vụ đó.

Giả sử hiện tại chi phí cho mỗi lần thay dầu ô tô là 800 nghìn đồng. Hãy ước tính chi phí cho mỗi lần thay dầu ô tô sau 5 năm nữa (kết quả tính theo đơn vị nghìn đồng và làm tròn đến hàng đơn vị).

Lời giải:

Chi phí cho mỗi lần thay dầu ô tô sau 5 năm nữa là:

C(5) = 800∙(1 + 0,04)⁵ $\approx$ 973 (nghìn đồng).

Vậy chi phí cho mỗi lần thay dầu ô tô sau 5 năm nữa khoảng 973 nghìn đồng.

Bài 6.59 trang 23 SBT Toán 11 Tập 2: Công thức tính khối lượng còn lại của một chất phóng xạ từ khối lượng ban đầu m₀ được cho bởi công thức:

$m\left(t\right)=m_0{\left(\frac{1}{2}\right)}^{\frac{t}{T}}$,

trong đó t là thời gian tính từ thời điểm ban đầu và T là chu kì bán rã của chất đó. Biết rằng chất phóng xạ polonium-210 có chu kì bán rã là 138 ngày. Từ khối lượng polonium-210 ban đầu 100 g, sau bao lâu khối lượng còn lại là:

a) 50 g?

b) 10 g?

(Kết quả tính theo ngày và làm tròn đến chữ số thập phân thứ hai).

Lời giải:

a) Thời gian để khối lượng polonium-210 còn 50 g là:

$50=100{\left(\frac{1}{2}\right)}^{\frac{t}{138}}$$\iff {\left(\frac{1}{2}\right)}^{\frac{t}{138}}=\frac{1}{2}$$\iff \frac{t}{138}=1\iff t=138$ (ngày).

Vậy sau 138 ngày thì khối lượng polonium-210 còn 50 g.

b) Thời gian để khối lượng polonium-210 còn 10 g là:

$10=100{\left(\frac{1}{2}\right)}^{\frac{t}{138}}$$\iff {\left(\frac{1}{2}\right)}^{\frac{t}{138}}=\frac{1}{10}$$\iff \frac{t}{138}={\log }_{\frac{1}{2}}\frac{1}{10}\iff t\approx 458,43$(ngày).

Vậy sau khoảng 458,43 ngày thì khối lượng polonium-210 còn 10 g.

Bài 6.60 trang 23 SBT Toán 11 Tập 2: Cent âm nhạc là một đơn vị trong thang lôgarit của cao độ hoặc khoảng tương đối. Một quãng tám bằng 1 200 cent. Công thức xác định chênh lệch khoảng thời gian (tính bằng cent) giữa hai nốt nhạc có tần số a và b là

$n=1200\cdot {\log }_2\frac{a}{b}$.

(Theo Algebra 2, NXB MacGraw-Hill, 2008)

a) Tìm khoảng thời gian tính bằng cent khi tần số thay đổi từ 443 Hz về 415 Hz.

b) Giả sử khoảng thời gian là 55 cent và tần số đầu là 225 Hz, hãy tìm tần số cuối cùng.

Lời giải:

a) Khoảng thời gian giữa hai nốt nhạc khi tần số thay đổi từ 443 Hz về 415 Hz là:

$n=1200\cdot {\log }_2\frac{443}{415}\approx 113$(cent).

Vậy khoảng thời gian giữa hai nốt nhạc khi tần số thay đổi từ 443 Hz về 415 Hz khoảng 113 cent.

b) Khoảng thời gian là 55 cent và tần số đầu là 225 Hz tức là n = 55, a = 225, thay vào công thức $n=1200\cdot {\log }_2\frac{a}{b}$ ta được $55=1200\cdot {\log }_2\frac{225}{b}$$\iff {\log }_2\frac{225}{b}=\frac{11}{240}$$\iff \frac{225}{b}=2^{\frac{11}{240}}$$\iff b\approx 218$ (Hz).

Vậy tần số cuối cùng cần tìm là 218 Hz.

Xem thêm lời giải SBT Toán 11 sách Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 5 trang 87

Bài 18: Lũy thừa với số mũ thực

Bài 19: Lôgarit

Bài 20: Hàm số mũ và hàm số lôgarit

Bài 21: Phương trình, bất phương trình mũ và lôgarit