Sách bài tập Toán 11 Bài 15 (Kết nối tri thức): Giới hạn của dãy số

Với giải sách bài tập Toán 11 Bài 15: Giới hạn của dãy số sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 11 Bài 15.

1 994 29/10/2024

Trang trước

Trang sau

Giải SBT Toán 11 Bài 15: Giới hạn của dãy số

Bài 5.1 trang 77 SBT Toán 11 Tập 1: Tính các giới hạn sau:

a) $\lim_{n \to + \infty} \frac{n^{2} + 1}{2 n^{2} + n + 2}$ ;

b) $\lim_{n \to + \infty} \frac{2^{n} + 3}{1 + 3^{n}}$ .

Lời giải:

a) $\lim_{n \to + \infty} \frac{n^{2} + 1}{2 n^{2} + n + 2} = \lim_{n \to + \infty} \frac{1 + \frac{1}{n^{2}}}{2 + \frac{1}{n} + \frac{2}{n^{2}}} = \frac{1}{2}$ .

b) $\lim_{n \to + \infty} \frac{2^{n} + 3}{1 + 3^{n}} = \lim_{n \to + \infty} \frac{{(\frac{2}{3})}^{n} + {(\frac{1}{3})}^{n - 1}}{{(\frac{1}{3})}^{n} + 1} = 0$ .

Bài 5.2 trang 78 SBT Toán 11 Tập 1: Tính các giới hạn sau:

a) $\lim_{n \to + \infty} (\sqrt{n^{2} + 2 n} - n - 2)$ ;

b) $\lim_{n \to + \infty} (2 + n^{2} - \sqrt{n^{4} + 1})$ ;

c) $\lim_{n \to + \infty} (\sqrt{n^{2} - n + 2} + n)$ ;

d) $\lim_{n \to + \infty} (3 n - \sqrt{4 n^{2} + 1})$ .

Lời giải:

a) $\lim_{n \to + \infty} (\sqrt{n^{2} + 2 n} - n - 2)$ $= \lim_{n \to + \infty} \frac{n^{2} + 2 n - {(n + 2)}^{2}}{\sqrt{n^{2} + 2 n} + n + 2}$

$= \lim_{n \to + \infty} \frac{- 2 n - 4}{\sqrt{n^{2} + 2 n} + n + 2} = \lim_{n \to + \infty} \frac{- 2 - \frac{4}{n}}{\sqrt{1 + \frac{2}{n}} + 1 + \frac{2}{n}} = \frac{- 2}{2} = - 1$ .

b) $\lim_{n \to + \infty} (2 + n^{2} - \sqrt{n^{4} + 1})$ $= \lim_{n \to + \infty} \frac{{(2 + n^{2})}^{2} - (n^{4} + 1)}{2 + n^{2} + \sqrt{n^{4} + 1}}$

$= \lim_{n \to + \infty} \frac{4 n^{2} + 3}{2 + n^{2} + \sqrt{n^{4} + 1}} = \lim_{n \to + \infty} \frac{4 + \frac{3}{n^{2}}}{\frac{2}{n^{2}} + 1 + \sqrt{1 + \frac{1}{n^{4}}}} = \frac{4}{2} = 2$ .

c) $\lim_{n \to + \infty} (\sqrt{n^{2} - n + 2} + n)$ $= \lim_{n \to + \infty} n (\sqrt{1 - \frac{1}{n} + \frac{2}{n^{2}}} + 1) = + \infty$ .

d) $\lim_{n \to + \infty} (3 n - \sqrt{4 n^{2} + 1})$ $= \lim_{n \to + \infty} n (3 - \sqrt{4 + \frac{1}{n^{2}}}) = + \infty$ .

Bài 5.3 trang 78 SBT Toán 11 Tập 1: Cho $u_{n} = \frac{1 + a + a^{2} + ... + a^{n}}{1 + b + b^{2} + ... + b^{n}}$ với a, b là các số thực thỏa mãn |a| < 1, |b| < 1. Tính $\lim_{n \to + \infty} u_{n}$ .

Lời giải:

Áp dụng công thức tính tổng n số hạng đầu của cấp số nhân, ta có:

$u_{n} = \frac{1 + a + a^{2} + ... + a^{n}}{1 + b + b^{2} + ... + b^{n}} = \frac{\frac{1 - a^{n + 1}}{1 - a}}{\frac{1 - b^{n + 1}}{1 - b}} = \frac{1 - b}{1 - a} . \frac{1 - a^{n + 1}}{1 - b^{n + 1}}$ .

Do đó, $\lim_{n \to + \infty} u_{n} = \lim_{n \to + \infty} (\frac{1 - b}{1 - a} . \frac{1 - a^{n + 1}}{1 - b^{n + 1}}) = \frac{1 - b}{1 - a}$ (do |a| < 1, |b| < 1).

Bài 5.4 trang 78 SBT Toán 11 Tập 1: Tính $\lim_{n \to + \infty} \frac{1 + 3 + 5 + ... + (2 n - 1)}{n^{2} + 2 n}$ .

Lời giải:

Ta có 1, 3, 5, ..., 2n – 1 là một cấp số cộng gồm n số hạng và có số hạng đầu u₁ = 1, công sai d = 2.

Khi đó, 1 + 3 + 5 + ... + (2n – 1) = $\frac{n (1 + 2 n - 1)}{2} = n^{2}$ .

Do đó, $\lim_{n \to + \infty} \frac{1 + 3 + 5 + ... + (2 n - 1)}{n^{2} + 2 n}$ $= \lim_{n \to + \infty} \frac{n^{2}}{n^{2} + 2 n} = \lim_{n \to + \infty} \frac{1}{1 + \frac{2}{n}} = 1$ .

Bài 5.5 trang 78 SBT Toán 11 Tập 1: Tính tổng $S = - 1 + \frac{1}{5} - \frac{1}{5^{2}} + ... + {(- 1)}^{n} \frac{1}{5^{n - 1}}$ + …

Lời giải:

Nhận thấy S là tổng của cấp số nhân lùi vô hạn (u_n) với số hạng đầu u₁ = – 1 và công bội q = $- \frac{1}{5}$ .

Do đó, $S = \frac{- 1}{1 - (- \frac{1}{5})} = \frac{- 1}{\frac{6}{5}} = - \frac{5}{6}$ .

Bài 5.6 trang 78 SBT Toán 11 Tập 1: Viết các số thập phân vô hạn tuần hoàn sau dưới dạng phân số:

a) 1,(03); b) 3,(23).

Lời giải:

a) 1,(03) = 1 + 0,03 + 0,0003 + ... + 0,00...03 + ...

$= 1 + \frac{3}{100} + \frac{3}{100^{2}} + .... + \frac{3}{100^{n}} + ....$ .

$= 1 + \frac{\frac{3}{100}}{1 - \frac{1}{100}} = 1 + \frac{1}{33} = \frac{34}{33}$

b) 3,(23) = 3 + 0,23 + 0,0023 + ... + 0,00...23 + ...

$= 3 + \frac{23}{100} + \frac{23}{100^{2}} + ... + \frac{23}{100^{n}} + ....$

$= 3 + \frac{\frac{23}{100}}{1 - \frac{1}{100}} = 3 + \frac{23}{99} = \frac{320}{99}$

Bài 5.7 trang 78 SBT Toán 11 Tập 1: Cho dãy số (u_n) với $u_{n} = \frac{\cos n}{n^{2}}$ . Tính $\lim_{n \to + \infty} u_{n}$ .

Lời giải:

Ta có $(u_{n}) = (\frac{\cos n}{n^{2}}) = \frac{(\cos n)}{n^{2}} \leq \frac{1}{n^{2}}$ .

Mà $\frac{1}{n^{2}} \to 0$ khi n → +∞ nên $\lim_{n \to + \infty} u_{n} = 0$ .

Bài 5.8 trang 78 SBT Toán 11 Tập 1: Cho tam giác A₁B₁C₁ có diện tích là 3 (đơn vị diện tích). Dựng tam giác A₂B₂C₂ bằng cách nối các trung điểm của các cạnh B₁C₁, C₁A₁, A₁B₁. Tiếp tục quá trình này, ta có các tam giác A₃B₃C₃, ..., A_nB_nC_n,... Kí hiệu s_n là diện tích của tam giác A_nB_nC_n.

a) Tính s_n.

b) Tính tổng s₁ + s₂ + ... + s_n + ...

Lời giải:

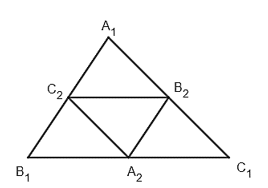
Cho tam giác A1B1C1 có diện tích là 3 (đơn vị diện tích)

Theo cách xác định tam giác A₂B₂C₂, ta có s₂ = $\frac{1}{4}$ s₁.

Tương tự, s₃ = $\frac{1}{4}$ s₂, ...., $s_{n} = \frac{1}{4} s_{n - 1}$ .

Vậy $s_{n} = {(\frac{1}{4})}^{n - 1} s_{1} = {(\frac{1}{4})}^{n - 1} .3 = 3 {(\frac{1}{4})}^{n - 1}$ .

b) Ta có s₁ + s₂ + ... + s_n + ... là tổng của cấp số nhân lùi vô hạn có số hạng đầu u₁ = 3 và công bội q = $\frac{1}{4}$ . Do đó

s₁ + s₂ + ... + s_n + ... = $\frac{3}{1 - \frac{1}{4}} = 4$ .

Bài 5.9 trang 78 SBT Toán 11 Tập 1: Cho dãy số (u_n) với u₁ = 2, $u_{n + 1} = u_{n} + \frac{2}{3^{n}}$ , n ≥ 1. Đặt v_n = u_{n + 1} – u_n.

a) Tính v₁ + v₂ + ... + v_n theo n.

b) Tính u_n theo n.

c) Tính $\lim_{n \to + \infty} u_{n}$ .

Lời giải:

a) Ta có v_n = u_{n + 1} – u_n = $(u_{n} + \frac{2}{3^{n}}) - u_{n} = \frac{2}{3^{n}}$ .

Do đó, v₁ + v₂ + ... + v_n = $\frac{2}{3} + \frac{2}{3^{2}} + ... + \frac{2}{3^{n}} = 2 (\frac{1}{3} + \frac{1}{3^{2}} + ... + \frac{1}{3^{n}})$

$= 2. \frac{1 - \frac{1}{3^{n + 1}}}{1 - \frac{1}{3}} = 3 (1 - \frac{1}{3^{n + 1}})$ .

b) Ta có v₁ + v₂ + ... + v_n = (u₂ – u₁) + (u₃ – u₂) + ... + (u_{n + 1} – u_n)

= u_{n +}₁ – u₁ = $(u_{n} + \frac{2}{3^{n}}) - 2 = u_{n} + \frac{2}{3^{n}} - 2$ .

Mà theo câu a có v₁ + v₂ + ... + v_n= $3 (1 - \frac{1}{3^{n + 1}})$ .

Do đó, $u_{n} + \frac{2}{3^{n}} - 2 = 3 (1 - \frac{1}{3^{n + 1}})$ . Từ đó suy ra $u_{n} = 5 - \frac{1}{3^{n - 1}}$ .

c) Ta có

$\lim_{n \to + \infty} u_{n} = \lim_{n \to + \infty} (5 - \frac{1}{3^{n - 1}}) = \lim_{n \to + \infty} (5 - {(\frac{1}{3})}^{n - 1}) = 5$ .

Bài 5.10 trang 78 SBT Toán 11 Tập 1: Cho dãy số (u_n) có tính chất $(u_{n} - \frac{n}{n + 1}) \leq \frac{1}{n^{2}}$ . Tính $\lim_{n \to + \infty} u_{n}$

Lời giải:

Ta có $(u_{n} - \frac{n}{n + 1}) \leq \frac{1}{n^{2}}$ , mà $\frac{1}{n^{2}} \to 0$ khi n → +∞ nên $\lim_{n \to + \infty} (u_{n} - \frac{n}{n + 1}) = 0$ .

Mặt khác,

$\lim_{n \to + \infty} (u_{n} - \frac{n}{n + 1}) = \lim_{n \to + \infty} u_{n} - \lim_{n \to + \infty} \frac{n}{n + 1} = \lim_{n \to + \infty} u_{n} - 1$ .

Vậy $\lim_{n \to + \infty} u_{n}$ = 1.

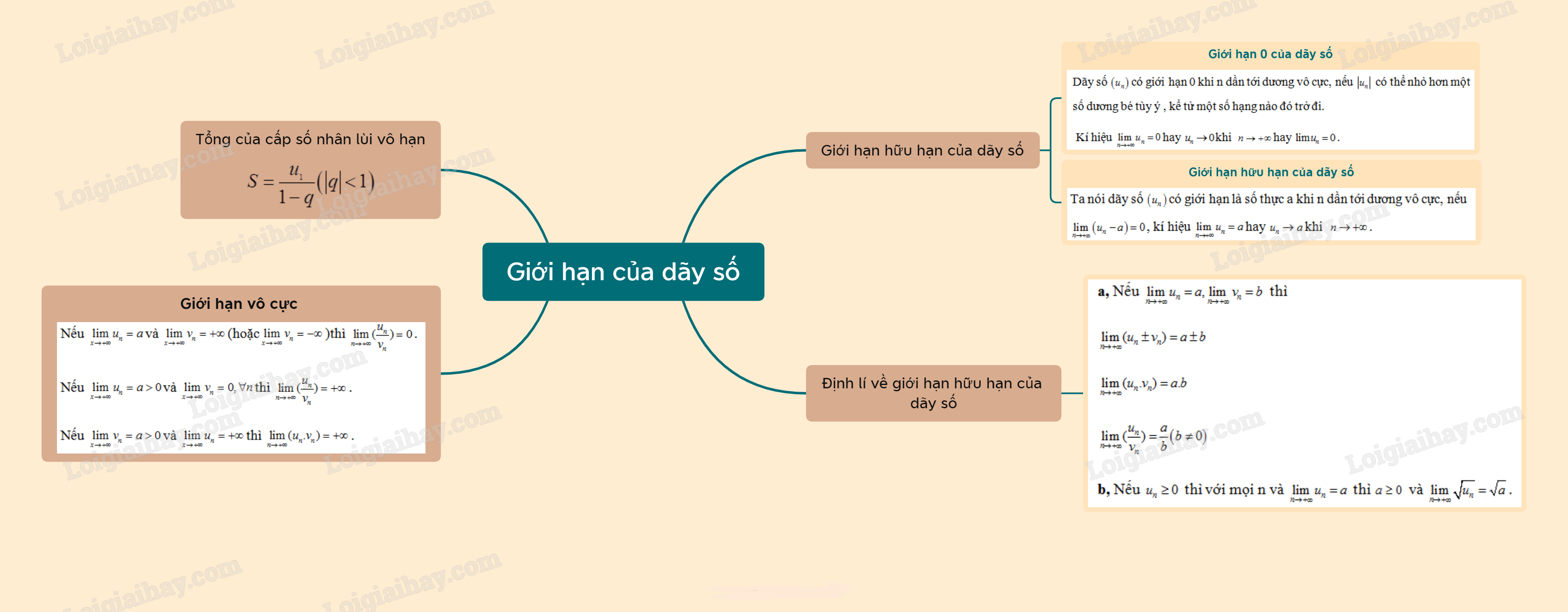
Lý thuyết Giới hạn của dãy số

1. Giới hạn hữu hạn của dãy số

Ta nói dãy số $(u_{n})$ có giới hạn 0 khi n dần tới dương vô cực, nếu $| u_{n} |$ có thể nhỏ hơn một số dương bé tùy ý , kể tử một số hạng nào đó trở đi, kí hiệu $lim_{n \to + \infty} u_{n} = 0$ hay $u_{n} \to 0$ khi $n \to + \infty$ .

Ta nói dãy số $(u_{n})$ có giới hạn là số thực a khi n dần tới dương vô cực, nếu $lim_{n \to + \infty} (u_{n} - a) = 0$ , kí hiệu $lim_{n \to + \infty} u_{n} = a$ hay $u_{n} \to a$ khi $n \to + \infty$ .

* Chú ý: Nếu $u_{n} = c$ (c là hằng số) thì $lim_{n \to + \infty} u_{n} = c$

2. Định lí về giới hạn hữu hạn của dãy số

a, Nếu $lim_{n \to + \infty} u_{n} = a, lim_{n \to + \infty} v_{n} = b$ thì

$lim_{n \to + \infty} (u_{n} \pm v_{n}) = a \pm b$

$lim_{n \to + \infty} (u_{n} . v_{n}) = a . b$

$lim_{n \to + \infty} (\frac{u_{n}}{v_{n}}) = \frac{a}{b} (b \neq 0)$

b, Nếu $u_{n} \geq 0$ thì với mọi n và $lim_{n \to + \infty} u_{n} = a$ thì $a \geq 0$ và $lim_{n \to + \infty} \sqrt{u_{n}} = \sqrt{a}$ .

3. Tổng của cấp số nhân lùi vô hạn

$S = \frac{u_{1}}{1 - q} (| q | < 1)$

4. Giới hạn vô cực của dãy số

Dãy số $(u_{n})$ được gọi là có giới hạn $+ \infty$ khi $n \to + \infty$ nếu $u_{n}$ có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi, kí hiệu $lim_{x \to + \infty} u_{n} = + \infty$ hay $u_{n} \to + \infty$ khi $n \to + \infty$ .

Dãy số $(u_{n})$ được gọi là có giới hạn $- \infty$ khi $n \to + \infty$ nếu $lim_{x \to + \infty} (- u_{n}) = + \infty$ , kí hiệu $lim_{x \to + \infty} u_{n} = - \infty$ hay $u_{n} \to - \infty$ khi $n \to + \infty$ .

*Quy tắc:

Nếu $lim_{x \to + \infty} u_{n} = a$ và $lim_{x \to + \infty} v_{n} = + \infty$ (hoặc $lim_{x \to + \infty} v_{n} = - \infty$ ) thì $lim_{n \to + \infty} (\frac{u_{n}}{v_{n}}) = 0$ .

Nếu $lim_{x \to + \infty} u_{n} = a > 0$ và $lim_{x \to + \infty} v_{n} = 0, \forall n$ thì $lim_{n \to + \infty} (\frac{u_{n}}{v_{n}}) = + \infty$ .

Nếu $lim_{x \to + \infty} v_{n} = a > 0$ và $lim_{x \to + \infty} u_{n} = + \infty$ thì $lim_{n \to + \infty} (u_{n} . v_{n}) = + \infty$ .

Xem thêm lời giải SBT Toán lớp 11 bộ sách Kết nối tri thức hay, chi tiết khác:

Bài 14: Phép chiếu song song

Bài tập cuối chương 4 trang 72

Bài 16: Giới hạn của hàm số

Bài 17: Hàm số liên tục

Bài tập cuối chương 5 trang 87

1 994 29/10/2024

Trang trước

Trang sau

Xem thêm các chương trình khác:

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3