Sách bài tập Toán 11 Bài 10 (Kết nối tri thức): Đường thẳng và mặt phẳng trong không gian

Giải SBT Toán 11 Bài 10: Đường thẳng và mặt phẳng trong không gian

Bài 4.1 trang 55 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD. Gọi O là giao điểm của AC và BD. Gọi M là một điểm bất kì thuộc cạnh SC.

a) Xác định giao tuyến của hai mặt phẳng (AMO) và (SCD).

b) Xác định giao tuyến của hai mặt phẳng (BMO) và (SCD).

Lời giải:

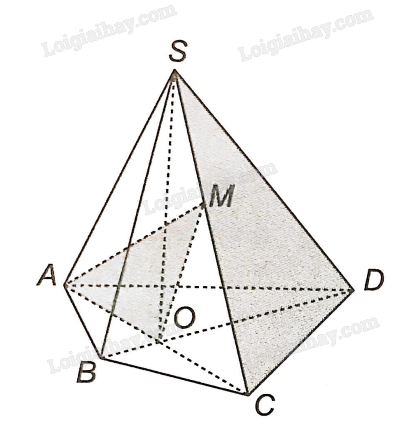
a) Ta thấy M thuộc AM, nằm trong mặt phẳng (AMO). M lại thuộc SC, nằm trong mặt phẳng (SCD). Vậy M là điểm chung thứ nhất của (AMO) và (SCD).

Ta thấy C thuộc đường thẳng AC (trùng với đường thẳng AO nên nó nằm trong mặt phẳng (AMO). C lại thuộc SC, nằm trong mặt phẳng (SCD). Vậy C là điểm chung thứ hai của (AMO) và (SCD).

Vậy nên MC (hay SC) là giao tuyến của hai mặt phẳng (AMO) và (SCD).

b) Ta thấy M thuộc BM, nằm trong mặt phẳng (BMO). M lại thuộc SC, nằm trong mặt phẳng (SCD). Vậy M là điểm chung thứ nhất của (BMO) và (SCD).

Ta thấy D thuộc đường thẳng BD (trùng với đường thẳng BO nên nó nằm trong mặt phẳng (BMO). D lại thuộc SD, nằm trong mặt phẳng (SCD). Vậy D là điểm chung thứ hai của (BMO) và (SCD).

Vậy nên MD là giao tuyến của hai mặt phẳng (BMO) và (SCD).

Bài 4.2 trang 55 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh BC, CD.

a) Xác định giao tuyến của hai mặt phẳng (SAM) và (SCD).

b) Xác định giao tuyến của hai mặt phẳng (SBN) và (SAD).

c) Xác định giao tuyến của hai mặt phẳng (SAM) và (SBN).

Lời giải:

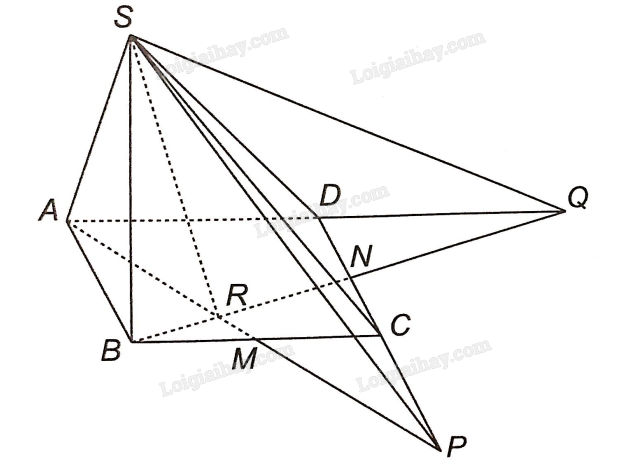
a) Ta thấy S là điểm chung thứ nhất của hai mặt phẳng (SAM) và (SCD).

Trong mặt phẳng (ABCD): Gọi P là giao điểm của AM và CD => P là điểm chung thứ hai của mặt phẳng (SAM) và (SCD).

Vậy SP là giao tuyến của (SAM) và (SCD).

b) Ta thấy S là điểm chung thứ nhất của hai mặt phẳng (SBN) và (SAD).

Trong mặt phẳng (ABCD): Gọi Q là giao điểm của AM và CD => P là điểm chung thứ hai của mặt phẳng (SBN) và (SAD).

Vậy SQ là giao tuyến của (SBN) và (SAD).

c) Ta thấy S là điểm chung thứ nhất của hai mặt phẳng (SAM) và (SBN).

Trong mặt phẳng (ABCD): Gọi R là giao điểm của AM và BN => R là điểm chung thứ hai của mặt phẳng (SAM) và (SBN).

Vậy SR là giao tuyến của (SAM) và (SBN).

Bài 4.3 trang 55 SBT Toán 11 Tập 1: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, AC. Gọi P là điểm thuộc cạnh AD sao cho AP = 2 DP. Xác định giao tuyến của hai mặt phẳng (MNP) và (BCD).

Lời giải:

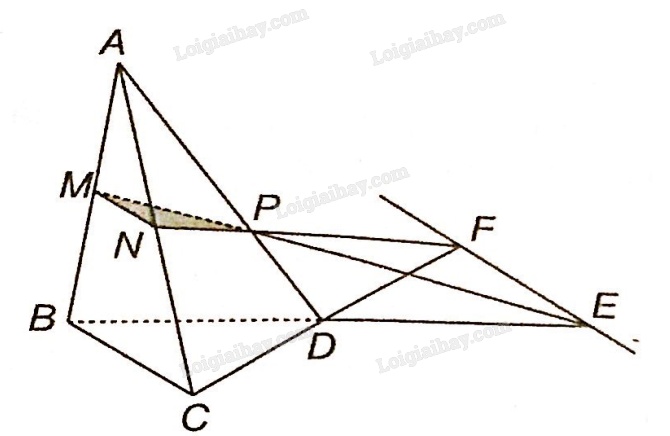
Trên mặt phẳng (ABD): gọi giao điểm của MP và BD là E. Vậy E là điểm chung thứ nhất của hai mặt phẳng (MNP) và (BCD)

Trên mặt phẳng (ACD): gọi giao điểm của NP và CD là F. Vậy F là điểm chung thứ hai của hai mặt phẳng (MNP) và (BCD).

Vậy giao tuyến của hai mặt phẳng (MNP) và (BCD) là đường thẳng EF.

Bài 4.4 trang 55 SBT Toán 11 Tập 1: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD. Gọi P là một điểm thuộc cạnh BC sao cho PC = 2PB.

a) Xác định giao điểm của đường thẳng BD và mặt phẳng (MNP).

b) Xác định giao điểm của đường thẳng AC và mặt phẳng (MNP).

c) Xác định giao điểm của đường thẳng AD và mặt phẳng (MNP).

Lời giải:

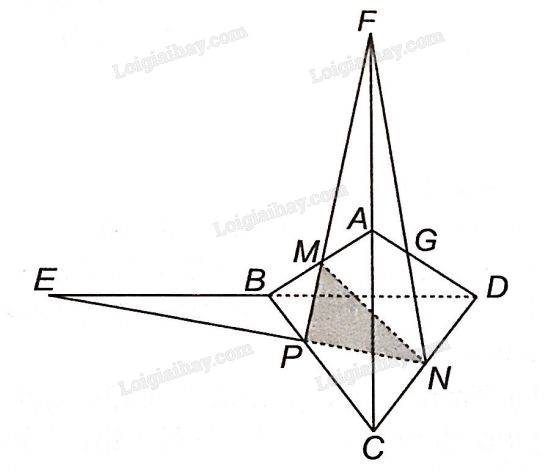
a) Trong mặt phẳng (BCD): Gọi E là giao điểm của BD và PN.

Vậy giao điểm của đường thẳng BD và mặt phẳng (MNP) là điểm E.

b) Trong mặt phẳng (ABC): gọi F là giao điểm của AC và MP.

Vậy giao điểm của đường thẳng AC và mặt phẳng (MNP) là điểm F.

c) Trong mặt phẳng (ADC): gọi G là giao điểm của AD và NF.

Vậy giao điểm của đường thẳng AD và mặt phẳng (MNP) là điểm G.

Bài 4.5 trang 55 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD. Gọi O là một điểm nằm trong tam giác SCD.

a) Xác định giao tuyến của hai mặt phẳng (SBO) và (SAC).

b) Xác định giao điểm của đường thẳng BO và mặt phẳng (SAC).

Lời giải:

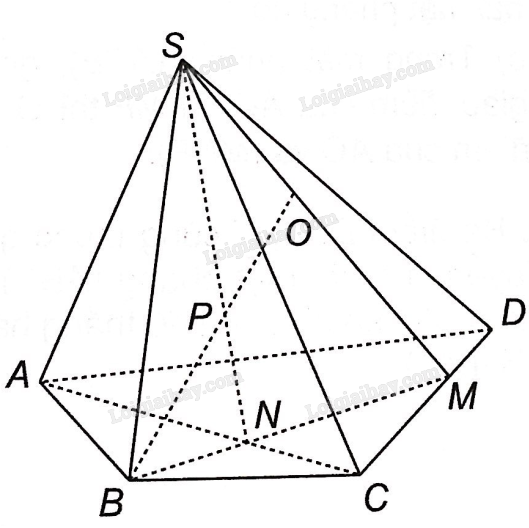
a) Ta thấy S là điểm chung đầu tiên của hai mặt phẳng (SBO) và (SAC).

Trong mặt phẳng (SCD): gọi M là điểm SO giao CD.

Trong mặt phẳng (ABCD): gọi N là giao điểm của BM và AC. Vậy N là điểm chung thứ hai của mặt phẳng (SAC) và (SBM) (trùng với mặt phẳng (SBO)).

Vậy giao tuyến của hai mặt phẳng (SBO) và (SAC) là SN.

b) Trong mặt phẳng (SAC): gọi P là giao điểm của đường thẳng SN và BO.

Vậy giao điểm của đường thẳng BO và mặt phẳng (SAC) là P.

Bài 4.6 trang 55 SBT Toán 11 Tập 1: Cho tứ diện ABCD. Gọi E, F là các điểm lần lượt thuộc cạnh AB, AC sao cho $\mathrm{A}\mathrm{E}=\frac{1}{2}\mathrm{B}\mathrm{E}$ và AF = 2CF. Gọi O là một điểm nằm trong tam giác BCD.

a) Xác định giao tuyến của hai mặt phẳng (OEF) và (ABD).

b) Xác định giao điểm (nếu có) của đường thẳng AD và mặt phẳng (OEF).

Lời giải:

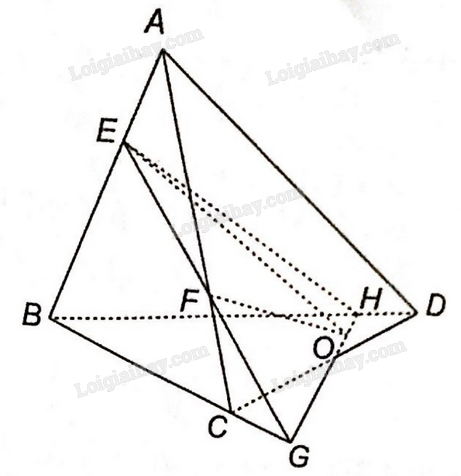
a) Ta thấy E thuộc AB, nằm trong mặt phẳng (ABD). Vậy E là điểm chung thứ nhất của hai mặt phẳng (ABD) và (OEF).

Trong mặt phẳng (ABC) gọi G là giao điểm của EF và BC.

Trong mặt phẳng (BCD), gọi H là giao điểm của BD và OG. Vậy H là một điểm chung của hai mặt phẳng (OEF) và (ABD)

Vậy EH là giao tuyến của hai mặt phẳng (OEF) và (ABD).

b) Trong mặt phẳng (ABD): Gọi I là giao điểm của EH và AD. Vậy I là giao điểm của AD và mặt phẳng (OEF).

Bài 4.7 trang 56 SBT Toán 11 Tập 1: Cho tứ diện ABCD và các điểm M, N, P lần lượt thuộc các cạnh AB, AC, AD. Gọi O là một điểm nằm trong tam giác BCD.

a) Xác định giao tuyến của hai mặt phẳng (ABO) và (ACD).

b) Xác định giao tuyến của hai mặt phẳng (ABO) và (MNP).

c) Xác định giao điểm của đường thẳng AO và mặt phẳng (MNP).

Lời giải:

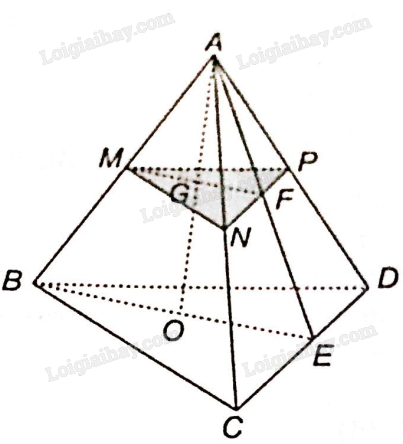
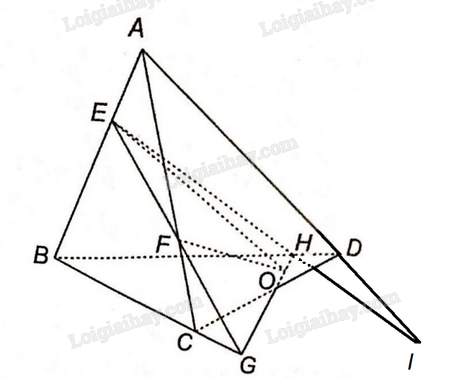
a) Ta thấy A là điểm chung đầu tiên của hai mặt phẳng (ABO) và (ACD).

Trong mặt phẳng (BCD): Gọi E là giao điểm của BO và CD. Vậy E là điểm chung thứ hai của hai mặt phẳng (ABO) và (ACD).

Vậy giao tuyến của hai mặt phẳng (ABO) và (ACD) là đường thẳng AE.

b) Ta thấy M thuộc AB, nằm trong mặt phẳng (ABO) vậy M là điểm chung thứ nhất của hai mặt phẳng (ABO) và (MNP).

Trong mặt phẳng (BCD): gọi E là giao điểm của BO và CD.

Trong mặt phẳng (ACD): gọi F là giao điểm của NP và AE. Vậy F là điểm chung thứ hai của (MNP) và (ABO).

Vậy giao tuyến của hai mặt phẳng (ABO) và (MNP) là đường thẳng MF.

c) Trong mặt phẳng (ABE) gọi G là giao điểm của AO và MF.

Vậy giao điểm của đường thẳng AO và mặt phẳng (MNP) là điểm G.

Bài 4.8 trang 56 SBT Toán 11 Tập 1: Cho hình tứ diện SABC và các điểm A’,B’,C’ lần lượt thuộc các cạnh SA, SB, SC. Giả sử hai đường thẳng B’C’ và BC cắt nhau tại D, hai đường thẳng C’A’ và CA cắt nhau tại E và hai đường thẳng A’B’ và AB cắt nhau tại F. Chứng minh rằng ba điểm D, E, F thẳng hàng.

Lời giải:

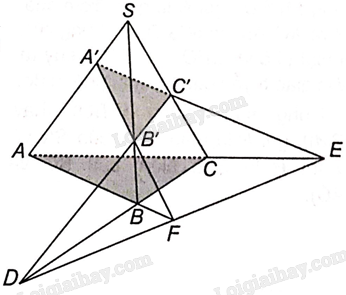
B’C’ và BC cắt nhau tại D nên D nằm trên giao tuyến của hai mặt phẳng (A’B’C’) và (ABC).

C’A’ và CA cắt nhau tại E nên E nằm trên giao tuyến của hai mặt phẳng (A’B’C’) và (ABC).

A’B’ và AB cắt nhau tại F nên F nằm trên giao tuyến của hai mặt phẳng (A’B’C’) và (ABC).

Vậy D, E, F cùng nằm trên giao tuyến của hai mặt phẳng (A’B’C’) và (ABC) nên ba điểm này thẳng hàng.

Bài 4.9 trang 56 SBT Toán 11 Tập 1: Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến d và một điểm O nằm ngoài cả hai mặt phẳng đó. Gọi A, B là hai điểm phân biệt thuộc mặt phẳng (P) sao cho AB cắt d tại C. Gọi D, E lần lượt là giao điểm của hai đường thẳng OA, OB và mặt phẳng (Q). Chứng minh rằng ba điểm C, D, E thẳng hàng.

Lời giải:

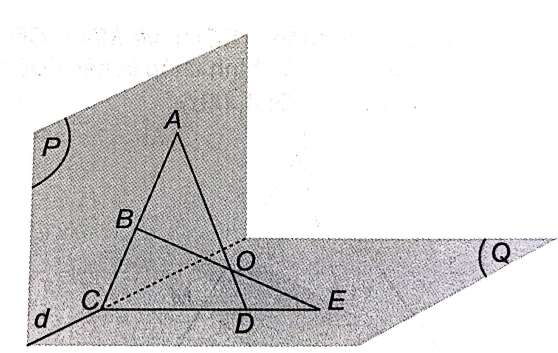
C thuộc AB nằm trong mặt phẳng (ABO), C lại nằm trên giao tuyến của (Q) và (P) nên C là điểm chung của mặt phẳng (ABO) và (Q). C nằm trên giao tuyến của (ABO) và (Q).

D là giao điểm của hai đường thẳng OA và mặt phẳng (Q) nên D nằm trên giao tuyến của (ABO) và (Q).

E là giao điểm của hai đường thẳng OB và mặt phẳng (Q) nên D nằm trên giao tuyến của (ABO) và (Q).

Vậy C, D, E cùng thuộc giao tuyến của hai mặt phẳng (ABO) và (Q) nên chúng thẳng hàng.

Bài 4.10 trang 56 SBT Toán 11 Tập 1: Đánh dấu một điểm trên mép của tờ giấy A4 và dùng kéo cắt một đường bất kì đi qua điểm đó (trong khi cắt không xoay kéo). Hãy giải thích vì sao đường cắt nhận được trên tờ giấy luôn là đường thẳng.

Lời giải:

Đường cắt là giao tuyến của mặt phẳng giấy và mặt phẳng lưỡi kéo, vậy nên đường cắt nhận được luôn là đường thẳng nếu không xoay kéo.

Bài 4.11 trang 56 SBT Toán 11 Tập 1: Bạn Huy đổ nước màu vào một chiếc bể cá có các mặt đều làm bằng kính phẳng. Sau một vài hôm nước bay hơi một phần và để lại trên thành bể cá các vệt màu như trong hình. Huy quan sát thấy rằng, dù bể cá có hình như thế nào, miễn là các mặt đều phẳng thì vệt màu trên mỗi thành bể đều là các đường thẳng. Hãy giải thích vì sao.

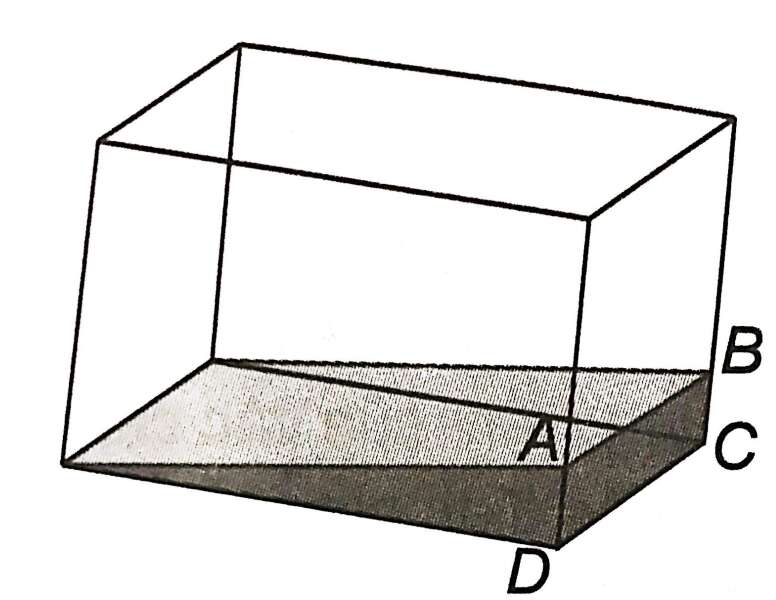
Lời giải:

Các vệt màu trên mỗi thành bể đều là giao tuyến của mặt nước và mặt bể vậy nên chúng là các đường thẳng.

Bài 4.12 trang 56 SBT Toán 11 Tập 1: Một số chiếc bàn có thiết kế khung sắt là hai hình chữ nhật có thể xoay quanh một trục, mặt bàn là một tấm gỗ phẳng được đặt lên phần khung như trong hình 4.6. Tính chất hình học nào giải thích việc mặt bàn có thể được giữ cố định bởi khung sắt? (Giả sử khung sắt chắc chắn và được đặt cân đối).

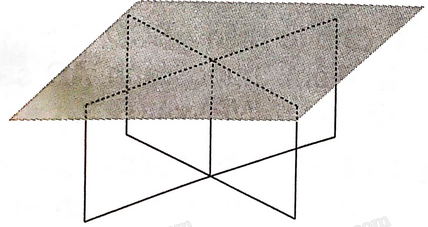
Lời giải:

Tính chất hình học nào giải thích việc mặt bàn có thể được giữ cố định bởi khung sắt là: Một mặt phẳng được xác định khi nó chứa hai đường thẳng cắt nhau.

Lý thuyết Đường thẳng và mặt phẳng trong không gian

1. Khái niệm mở đầu

Hình ảnh về mặt phẳng

- Để biểu diễn mặt phẳng ta thường dùng 1 hình bình hành như hình vẽ:

- Để kí hiệu mặt phẳng ta dùng chữ cái in hoa hoặc chữ cái Hy Lạp đặt trong dấu ngoặc ( ).

VD: Mặt phẳng (P), mặt phẳng ($\alpha$).

- Điểm A thuộc mặt phẳng (P), ta kí hiệu $A\in (P)$, điểm B không thuộc mặt phẳng (P) ta kí hiệu $B\notin (P)$.Nếu $A\in (P)$ta còn nói A nằm trên (P) hoặc (P) chứa A hoặc (P) đi qua A.

*Quy tắc biểu diễn hình:

- Hình biểu diễn của đường thẳng là đường thẳng, của đoạn thẳng là đoạn thẳng.

- Hình biểu diễn của hai đường thẳng song song là 2 đường thẳng song song, của 2 đường thẳng cắt nhau là 2 đường thẳng cắt nhau.

- Hình biểu diễn giữ nguyên quan hệ liên thuộc giữa điểm và đường thẳng.

- Dùng nét liền để biểu diễn cho đường nhìn thấy và nét đứt đoạn để biểu diễn cho đường bị che khuất.

2. Các tính chất thừa nhận

- Có một và chỉ một đường thẳng đi qua hai điểm phân biệt.

- Có một và chỉ một mặt phẳng đi qua 3 điểm không thẳng hàng.

- Tồn tại 4 điểm không cùng thuộc một mặt phẳng.

- Nếu có một đường thẳng có 2 điểm phân biệt thuộc một mặt phẳng thì tất cả các điểm của đường thẳng đều thuộc mặt phẳng đó.

- Nếu mọi điểm của đường thẳng d đều thuộc mặt phẳng (P) thì ta nói d nằm trong (P) hoặc (P) chứa d. Kí hiệu $d\subset (P)$ hoặc .

- Nếu hai mặt phẳng phân biệt có điểm chung thì các điểm chung của hai mặt phẳng là một đường thẳng đi qua điểm chung đó. Đường thẳng đó được gọi là giao tuyến, kí hiệu .

- Trên mỗi mặt phẳng, tất cả các kết quả đã biết trong hìn$d=(P)\cap (Q)$h học phẳng đều đúng.

3. Xác định một mặt phẳng

Một mặt phẳng hoàn toàn được xác định khi biết nó đi qua 3 điểm không thẳng hàng.

Một mặt phẳng được hoàn toàn xác định khi biết nó đi qua một điểm và chứa 1 đường thẳng không đi qua điểm đó.

Một mặt phẳng được hoàn toàn xác định khi biết nó chứa hai đường thẳng cắt nhau.

4. Hình chóp và hình tứ diện

Cho đa giác lồi $A_1{A}_2...A_n$ và một điểm S nằm ngoài mặt phẳng chứa đa giác đó. Nối S với các đỉnh $A_1,A_2,...,A_n$để được n tam giác $S{A}_1{A}_2,S{A}_2{A}_3,...,S{A}_n{A}_1$. Hình gồm n tam giác $S{A}_1{A}_2,S{A}_2{A}_3,...,S{A}_n{A}_1$và đa giác $A_1{A}_2...A_n$được gọi là hình chóp và kí hiệu là $S.A_1{A}_2...A_n$.

Trong hình chóp $S.A_1{A}_2...A_n$điểm S được gọi là đỉnh và đa giác$A_1{A}_2...A_n$ được gọi là mặt đáy, các tam giác $S{A}_1{A}_2,S{A}_2{A}_3,...,S{A}_n{A}_1$được gọi là các mặt bên; các cạnh $S{A}_1,S{A}_2,...,S{A}_n$được gọi là cạnh bên; các cạnh$A_1{A}_2,A_2{A}_3...,A_n{A}_1$ được gọi là các cạnh đáy.

VD: Hình chóp tứ giác S.ABCD

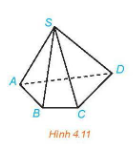
Cho 4 điểm A, B, C, D không đồng phẳng. Hình gồm 4 tam giác ABC, ABD, ACD và BCD được gọi là hình tứ diện, kí hiệu là ABCD.

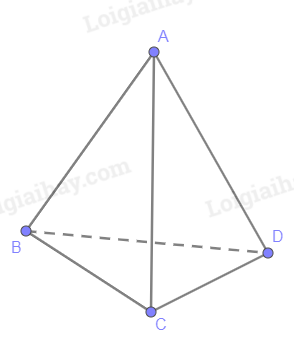
Trong đó, các điểm A, B, C, D được gọi các đỉnh của tứ diện, các đoạn thẳng AB, BC, CD, DA, BD,AC được gọi là cạnh của tứ diện; các tam giác ABC, ABD, ACD và BCD gọi là mặt của tứ diện.

Hai cạnh không có đỉnh chung được gọi là hai cạnh đối diện, đỉnh không nằm trên một mặt gọi là đỉnh đối diện với mặt đó.

Xem thêm lời giải SBT Toán 11 sách Kết nối tri thức hay, chi tiết khác:

Bài 11: Hai đường thẳng song song

Bài 12: Đường thẳng và mặt phẳng song song

Bài 13: Hai mặt phẳng song song

Bài 14: Phép chiếu song song

Bài tập cuối chương 4 trang 72