Nội dung bài viết

    Xem thêm

    Sách bài tập Toán 11 Bài 28 (Kết nối tri thức): Biến cố hợp, biến cố giao, biến cố độc lập

    Với giải sách bài tập Toán 11 Bài 28: Biến cố hợp, biến cố giao, biến cố độc lập sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 11 Bài 28.

    1 584 29/10/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 11 Bài 28: Biến cố hợp, biến cố giao, biến cố độc lập

    Bài 8.1 trang 45 SBT Toán 11 Tập 2: Một hộp đựng 70 tấm thẻ, đánh số từ 1 đến 70. Rút ngẫu nhiên một tấm thẻ. Kí hiệu a là số ghi trên thẻ. Gọi A là biến cố: “a là ước của 28”, B là biến cố: “a là ước của 70”. Xét biến cố C: “a là ước của 14”. Chứng tỏ C là biến cố giao của A và B.

    Lời giải:

    Ta có A = {1; 2; 4; 7; 14; 28}; B = {1; 2; 5; 7; 10; 14; 35; 70}; C = {1; 2; 7; 14}.

    Ta có A ∩ B = {1; 2; 7; 14}.

    Vậy C là biến cố giao của A và B.

    Bài 8.2 trang 46 SBT Toán 11 Tập 2: Một chiến hạm có ba bộ phận A, B, C có tầm quan trọng khác nhau. Chiến hạm sẽ bị chìm khi và chỉ khi:

    - Hoặc có một quả ngư lôi bắn trúng bộ phận A;

    - Hoặc có hai quả ngư lôi bắn trúng bộ phận B;

    - Hoặc có ba quả ngư lôi bắn trúng bộ phận C.

    Giả sử có hai quả ngư lôi bắn trúng chiến hạm. Xét hai biến cố K: “Hai quả trúng vào C”, H: “Một quả trúng vào B, một quả trúng vào C”.

    Gọi M là biến cố: “Chiến hạm không bị chìm”. Chứng tỏ rằng M là biến cố hợp của H và K.

    Lời giải:

    Nếu biến cố H xảy ra thì B trúng một quả ngư lôi, C trúng một quả ngư lôi. Từ điều kiện ta thấy chiến hạm không bị chìm (biến cố M xảy ra).

    Nếu biến cố K xảy ra thì C trúng hai quả ngư lôi. Từ điều kiện ta thấy chiến hạm không bị chìm (biến cố M xảy ra).

    Ngược lại giả sử chiến hạm không bị chìm, khi đó cả hai quả hoặc trúng vào C (biến cố K xảy ra) hoặc chỉ một quả trúng vào B và quả còn lại không trúng A, tức là trúng C (biến cố H xảy ra).

    Vậy M là biến cố hợp của H và K.

    Bài 8.3 trang 46 SBT Toán 11 Tập 2: Có bốn chiếc hộp I, II, III, IV mỗi hộp đựng 10 tấm thẻ, đánh số từ 1 đến 10. Từ mỗi hộp rút ngẫu nhiên một tấm thẻ. Gọi a, b, c, d là số ghi trên thẻ tương ứng rút từ I, II, III, IV.

    Xét các biến cố sau:

    A: “a là số chẵn”; B: “b là số chẵn”; C: “c là số chẵn”; D: “d là số chẵn”;

    E: “ad là số lẻ”; F: “bc là số lẻ”; G: “ad – bc là số chẵn”.

    Chứng tỏ rằng:

    a) E = A¯D¯ ; F = B¯C¯ ;

    b) G=EF∪E¯F¯.

    Lời giải:

    a) ad là số lẻ khi và chỉ khi cả a và d đều là số lẻ, tức là không xảy ra cả biến cố A và biến cố D. Vậy E=A¯D¯ .

    Tương tự bc là số lẻ khi và chỉ khi cả b và c đều là số lẻ, tức là không xảy ra cả biến cố B và biến cố C. Vậy F=B¯C¯ .

    b) Giả sử G xảy ra tức là ad và bc có cùng tính chẵn, lẻ.

    Nếu ad là số lẻ, bc là số lẻ thì E và F đều xảy ra. Do đó EF xảy ra.

    Nếu ad là số chẵn, bc là số chẵn thì E và F đều không xảy ra. Do đó E¯F¯ xảy ra.

    Ngược lại, nếu EF xảy ra thì ad là số lẻ, bc là số lẻ. Suy ra ad – bc là số chẵn.

    Nếu E¯F¯ xảy ra thì ad là số chẵn, bc là số chẵn. Suy ra ad – bc là số chẵn.

    Vậy G=EF∪E¯F¯.

    Bài 8.4 trang 46 SBT Toán 11 Tập 2: Hai bạn Sơn và Tùng, mỗi bạn gieo đồng thời hai đồng xu cân đối. Xét hai biến cố sau:

    E: “Cả hai đồng xu bạn Sơn gieo đều ra mặt sấp”.

    F: “Hai đồng xu bạn Tùng gieo có một sấp, một ngửa”.

    Chứng tỏ rằng E và F độc lập.

    Lời giải:

    Ta có Ω = {SS; SN; NS; NN}, n(Ω) = 4.

    E = {SS}, n(E) = 1, suy ra P(E) = 14.

    F = {SN; NS}, n(F) = 2, suy ra P(F) = 24=12 .

    Nếu F xảy ra thì P(E) = 14 ; nếu F không xảy ra thì P(E) = 14.

    Nếu E xảy ra thì P(F) = 12 ; nếu E không xảy ra thì P(F) = 12.

    Việc xảy ra hay không xảy ra của biến cố này không ảnh hưởng tới xác suất xảy ra của biến cố kia.

    Vậy E và F độc lập.

    Bài 8.5 trang 46 SBT Toán 11 Tập 2: Một chiếc túi có 12 tấm thẻ được đánh số từ 1 đến 12. Bạn Hòa rút ngẫu nhiên một tấm thẻ trong túi để sang bên cạnh. Tiếp theo, bạn Bình rút ngẫu nhiên tiếp một tấm thẻ. Xét hai biến cố sau:

    M: “Bạn Hòa rút được tấm thẻ ghi số lẻ”;

    N: “Bạn Bình rút được tấm thẻ ghi số chẵn”.

    Chứng tỏ rằng hai biến cố M và N không độc lập.

    Lời giải:

    Trong các số từ 1 đến 12, có 6 số lẻ là 1; 3; 5; 7; 9; 11 và 6 số chẵn là 2; 4; 6; 8; 10; 12.

    Nếu M xảy ra, tức là bạn Hòa rút được tấm thẻ ghi số lẻ thì sau đó trong túi còn 11 tấm thẻ với 5 thẻ ghi số lẻ và 6 thẻ ghi số chẵn. Vậy P(N) = 611.

    Nếu M không xảy ra, tức là bạn Hòa rút được tấm thẻ ghi số chẵn thì sau đó trong túi còn 11 tấm thẻ trong đó 6 tấm thẻ ghi số lẻ và 5 tấm thẻ ghi số chẵn. Vậy P(N) = 511 .

    Như vậy xác suất của N thay đổi tùy theo M xảy ra hay M không xảy ra. Do đó M và N không độc lập.

    Lý thuyết Biến cố hợp, biến cố giao, biến cố độc lập

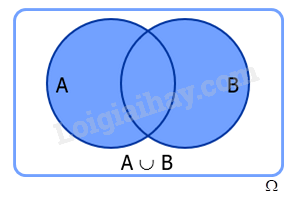
    1. Biến cố hợp

    Cho A và B là hai biến cố. Biến cố: “A hoặc B xảy ra” được gọi là biến cố hợp của A và B, kí hiệu là A∪B.

    Biến cố hợp của A và B là tập con A∪B của không gian mẫu Ω.

    Lý thuyết Biến cố hợp, biến cố giao, biến cố độc lập (Kết nối tri thức 2024) hay, chi tiết | Toán lớp 11 (ảnh 1)

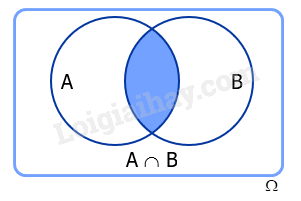
    2. Biến cố giao

    Cho A và B là hai biến cố. Biến cố: “Cả A và B đều xảy ra” được gọi là biến cố giao của A và B, kí hiệu là AB.

    Biến cố giao của A và B là tập con A∩B của không gian mẫu Ω.

    Lý thuyết Biến cố hợp, biến cố giao, biến cố độc lập (Kết nối tri thức 2024) hay, chi tiết | Toán lớp 11 (ảnh 2)

    3. Biến cố độc lập

    Cặp biến cố A và B được gọi là độc lập nếu việc xảy ra hay không xảy ra của biến cố này không ảnh hưởng tới xác suất xảy ra của biến cố kia.

    Chú ý: Nếu cặp biến cố A và B độc lập thì các cặp biến cố: A và B¯; A¯ và B; A¯ và B¯ cũng độc lập.

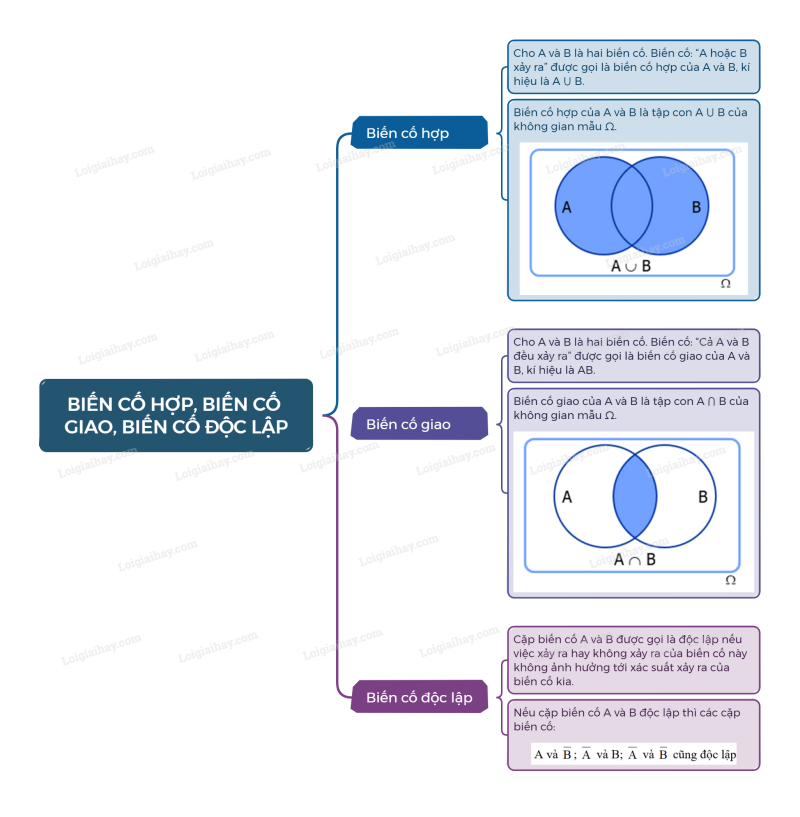
    Sơ đồ tư duy Biến cố hợp, biến cố giao, biến cố độc lập

    Lý thuyết Biến cố hợp, biến cố giao, biến cố độc lập (Kết nối tri thức 2024) hay, chi tiết | Toán lớp 11 (ảnh 3)

    Xem thêm lời giải SBT Toán 11 sách Kết nối tri thức hay, chi tiết khác:

    Bài 29: Công thức cộng xác suất

    Bài 30: Công thức nhân xác suất cho hai biến cố độc lập

    Bài tập cuối chương 8

    Bài 31: Định nghĩa và ý nghĩa của đạo hàm

    Bài 32: Các quy tắc tính đạo hàm

    Tham khảo các loạt bài Toán 11 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 584 29/10/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: