Sách bài tập Toán 11 Bài 5 (Kết nối tri thức): Dãy số

Giải SBT Toán 11 Bài 5: Dãy số

Bài 2.1 trang 33 SBT Toán 11 Tập 1: Viết năm số hạng đầu tiên của mỗi dãy số (u_n) sau:

a) $u_n={\left(-1\right)}^{n-1}\frac{n}{2n-1}$;

b) u₁ = 1, u_n = n – u_{n – 1} (n ≥ 2).

Lời giải:

a) $u_1={\left(-1\right)}^0.\frac{1}{2.1-1}=1$; $u_2={\left(-1\right)}^{2-1}.\frac{2}{2.2-1}=-\frac{2}{3}$; $u_3={\left(-1\right)}^{3-1}.\frac{3}{2.3-1}=\frac{3}{5}$;

$u_4={\left(-1\right)}^{4-1}.\frac{4}{2.4-1}=-\frac{4}{7}$; $u_5={\left(-1\right)}^{5-1}.\frac{5}{2.5-1}=\frac{5}{9}$.

b) u₁ = 1; u₂ = 2 – u₁ = 2 – 1 = 1; u₃ = 3 – u₂ = 3 – 1 = 2; u₄ = 4 – u₃ = 4 – 2 = 2;

u₅ = 5 – u₄ = 5 – 2 = 3.

Bài 2.2 trang 33 SBT Toán 11 Tập 1: Xét tính tăng, giảm của mỗi dãy số sau:

a) u_n = n² + n + 1;

b) $u_n=\frac{2n+5}{n+2}$;

c) $u_n=\frac{{\left(-1\right)}^{n-1}}{n^2+1}$.

Lời giải:

a) Ta có u_{n + 1} – u_n = [(n + 1)² + (n + 1) + 1] – (n² + n + 1)

= n² + 2n + 1 + n + 1 + 1 – n² – n – 1

= 2n + 2 > 0, ∀ n ≥ 1.

Do đó, u_{n + 1} > u_n ∀ n ≥ 1. Vậy (u_n­) là dãy số tăng.

b) Ta có $u_{n+1}-u_n=\frac{2\left(n+1\right)+5}{n+1+2}-\frac{2n+5}{n+2}$$=\frac{2n+7}{n+3}-\frac{2n+5}{n+2}$

$=\frac{\left(2n+7\right)\left(n+2\right)-\left(2n+5\right)\left(n+3\right)}{\left(n+3\right)\left(n+2\right)}$$=\frac{-1}{\left(n+3\right)\left(n+2\right)}<\mathrm{0,}\forall n\ge 1$.

Do đó, u_{n + 1} < u_n ∀ n ≥ 1. Vậy (u_n­) là dãy số giảm.

c) Ta có $u_{n+1}-u_n=\frac{{\left(-1\right)}^{n+1-1}}{{\left(n+1\right)}^2+1}-\frac{{\left(-1\right)}^{n-1}}{n^2+1}$$=\frac{{\left(-1\right)}^n}{{\left(n+1\right)}^2+1}+\frac{{\left(-1\right)}^n}{n^2+1}$

$={\left(-1\right)}^n\left(\frac{1}{{\left(n+1\right)}^2+1}+\frac{1}{n^2+1}\right)$.

Vì $\frac{1}{{\left(n+1\right)}^2+1}+\frac{1}{n^2+1}>0\forall n\ge 1$ nên hiệu u_{n + 1} – u_n dương hay âm phụ thuộc vào n, cụ thể là dương khi n chẵn và âm khi n lẻ.

Do đó, dãy số (u_n) không tăng cũng không giảm.

Bài 2.3 trang 33 SBT Toán 11 Tập 1: Xét tính bị chặn của các dãy số sau:

a) $u_n=\frac{n}{2n+1}$;

b) u_n = n² + n – 1;

c) u_n = – n² + 1.

Lời giải:

a) Ta có $u_n=\frac{n}{2n+1}\ge \frac{1}{3}\forall n\ge 1$.

Lại có $u_n=\frac{n}{2n+1}=\frac{\frac{1}{2}\left(2n+1\right)-\frac{1}{2}}{2n+1}=\frac{1}{2}-\frac{\frac{1}{2}}{2n+1}=\frac{1}{2}-\frac{1}{2\left(2n+1\right)}$. Suy ra $u_n\le \frac{1}{2}\forall n\ge 1$.

Do đó $\frac{1}{3}\le u_n\le \frac{1}{2}\forall n\ge 1$. Vậy (u_n) là dãy số bị chặn.

b) Ta có n – 1 ≥ 0 với mọi n ≥ 1 và n² ≥ 0 với mọi n.

Do đó, u_n = n² + n – 1 ≥ 1.

Vậy dãy số (u_n) bị chặn dưới bởi 1 với mọi n ≥ 1.

c) Ta có u_n = – n² + 1 < 1 với mọi n ≥ 1.

Vậy dãy số (u_n) bị chặn trên bởi 1 với mọi n ≥ 1.

Bài 2.4 trang 34 SBT Toán 11 Tập 1: Để tính xấp xỉ giá trị $\sqrt{p}$, người ta có thể dùng dãy số cho bởi hệ thức truy hồi sau:

u₁ = k, $u_n=\frac{1}{2}\left(u_{n-1}+\frac{p}{u_{n-1}}\right)$ với n ≥ 2,

ở đó k là một giá trị dự đoán ban đầu của $\sqrt{p}$.

Sử dụng hệ thức truy hồi này, hãy tính xấp xỉ các giá trị sau bằng cách tính u₅ và tính sai số tuyệt đối khi so với giá trị tính bằng máy tính cầm tay (làm tròn kết quả đến chữ số thập phân thứ năm).

a) $\sqrt{5}$ (lấy k = 3);

b) $\sqrt{8}$ (lấy k = 3).

Lời giải:

a) Với p = 5 thì $\sqrt{5}$≈ 2,23607. Nếu ta chọn u₁ = 3 thì ta có:

u₁ = 3

$u_2=\frac{1}{2}\left(u_1+\frac{5}{u_1}\right)=\frac{1}{2}\left(3+\frac{5}{3}\right)$≈ 2,3333

$u_3=\frac{1}{2}\left(u_2+\frac{5}{u_2}\right)=\frac{1}{2}\left(\mathrm{2,3333}+\frac{5}{\mathrm{2,3333}}\right)$≈ 2,2381

$u_4=\frac{1}{2}\left(u_3+\frac{5}{u_3}\right)=\frac{1}{2}\left(\mathrm{2,2381}+\frac{5}{\mathrm{2,2381}}\right)$≈ 2,2361

$u_5=\frac{1}{2}\left(u_4+\frac{5}{u_4}\right)=\frac{1}{2}\left(\mathrm{2,2361}+\frac{5}{\mathrm{2,2361}}\right)$≈ 2,2361

Sai số tuyệt đối xấp xỉ bằng 2,2361 – 2,23607 = 0,00003.

b) Với p = 8 thì $\sqrt{8}$ ≈ 2,82843. Nếu ta chọn u₁ = 3 thì ta có:

u₁ = 3

$u_2=\frac{1}{2}\left(u_1+\frac{8}{u_1}\right)=\frac{1}{2}\left(3+\frac{8}{3}\right)$≈ 2,8333

$u_3=\frac{1}{2}\left(u_2+\frac{8}{u_2}\right)=\frac{1}{2}\left(\mathrm{2,8333}+\frac{8}{\mathrm{2,3333}}\right)$≈ 2,8284

$u_4=\frac{1}{2}\left(u_3+\frac{8}{u_3}\right)=\frac{1}{2}\left(\mathrm{2,8284}+\frac{8}{\mathrm{2,8284}}\right)$≈ 2,8284

$u_5=\frac{1}{2}\left(u_4+\frac{8}{u_4}\right)=\frac{1}{2}\left(\mathrm{2,8284}+\frac{5}{\mathrm{2,8284}}\right)$≈ 2,8284

Sai số tuyệt đối xấp xỉ bằng 2,8284 – 2,82843 = 0,00003.

Bài 2.5 trang 34 SBT Toán 11 Tập 1: Cho dãy số (u_n) xác định bằng hệ thức truy hồi

u₁ = 1, u_{n + 1} = u_n + (n + 1).

a) Mỗi số hạng của dãy số này gọi là một số tam giác. Viết bảy số tam giác đầu.

b) Biết rằng 1 + 2 + ... + n = $\frac{n\left(n+1\right)}{2}$. Hãy chứng tỏ công thức của số hạng tổng quát là $u_{n+1}=\frac{\left(n+1\right)\left(n+2\right)}{2}$.

c) Chứng minh rằng u_{n + 1} + u_n = (n + 1)², tức là tổng của hai số tam giác liên tiếp là một số chính phương.

Lời giải:

a) Bảy số tam giác đầu là u₁ = 1; u₂ = u₁ + (1 + 1) = 1 + 2 = 3;

u₃ = u₂ + (2 + 1) = 3 + 3 = 6; u₄ = u₃ + (3 + 1) = 6 + 4 = 10;

u₅ = u₄ + (4 + 1) = 10 + 5 = 15; u₆ = u₅ + (5 + 1) = 15 + 6 = 21;

u₇ = u₆ + (6 + 1) = 21 + 7 = 28.

b) Từ kết quả ở câu a, ta nhận thấy u₁ = 1, u₂ = 1 + 2, u₃ = 1 + 2 + 3, u₄ = 1 + 2 + 3 + 4, ...

Từ đó suy ra u_{n + 1} = 1 + 2 + ... + n + (n + 1)

$=\frac{n\left(n+1\right)}{2}+\left(n+1\right)=\frac{n\left(n+1\right)+2\left(n+1\right)}{2}=\frac{\left(n+1\right)\left(n+2\right)}{2}$.

Vậy $u_{n+1}=\frac{\left(n+1\right)\left(n+2\right)}{2}$.

c) Theo công thức ở câu b) ta có:

$u_{n+1}+u_n=\frac{\left(n+1\right)\left(n+2\right)}{2}+\frac{n\left(n+1\right)}{2}=\frac{\left(n+1\right)\left(\left(n+2\right)+n\right)}{2}$$=\frac{\left(n+1\right).2\left(n+1\right)}{2}={\left(n+1\right)}^2$.

Vậy tổng của hai số tam giác liên tiếp là một số chính phương.

Bài 2.6 trang 34 SBT Toán 11 Tập 1: Giá của một chiếc máy photocopy lúc mới mua là 50 triệu đồng. Biết rằng giá trị của nó sau mỗi năm sử dụng chỉ còn 75% giá trị trong năm liền trước đó. Tính giá trị còn lại của chiếc máy photocopy đó sau mỗi năm, trong khoảng thời gian 5 năm kể từ khi mua.

Lời giải:

Giá trị của máy photocopy sau 1 năm sử dụng là

T₁ = 50 . 75% = 37,5 (triệu đồng).

Giá trị của máy photocopy sau 2 năm sử dụng là

T₂ = T₁ . 75% = 37,5 . 75% = 28,125 (triệu đồng).

Giá trị của máy photocopy sau 3 năm sử dụng là

T₃ = T₂ . 75% = 28,125 .75% = 21,09375 (triệu đồng).

Giá trị của máy photocopy sau 4 năm sử dụng là

T₄ = T₃ . 75% = 21,0375 . 75% ≈ 15,8203 (triệu đồng).

Giá trị của máy photocopy sau 5 năm sử dụng là

T₅ = T₄ . 75% ≈ 15,8203 . 75% ≈ 11,8652 (triệu đồng).

Tổng quát, giá trị của máy photocopy sau n năm sử dụng là

T_n = T₁ . (0,75)^{n – 1} (triệu đồng).

Bài 2.7 trang 34 SBT Toán 11 Tập 1: Nếu tỉ lệ lạm phát là 3,5% mỗi năm và giá trung bình của một căn hộ chung cư mới tại thời điểm hiện tại là 2,5 tỉ đồng thì giá trung bình của một căn hộ chung cư mới sau n năm nữa được cho bởi công thức

A_n = 2,5 . (1,035)ⁿ (tỉ đồng).

Tìm giá trung bình của một căn hộ chung cư mới sau 5 năm nữa.

Lời giải:

Giá trung bình của một căn hộ chung cư mới sau 5 năm là

A₅ = 2,5 . (1,035)⁵ ≈ 2,9692 (tỉ đồng).

Bài 2.8 trang 34 SBT Toán 11 Tập 1: Bác An gửi tiết kiệm 200 triệu đồng kì hạn 3 tháng, với lãi suất 3% một năm. Số tiền (triệu đồng) cả vốn lẫn lãi mà bác An nhận được sau n quý (mỗi quý là 3 tháng) sẽ là

$A_n=200{\left(1+\frac{\mathrm{0,03}}{4}\right)}^n$, n = 0, 1, 2, ...

a) Viết ba số hạng đầu của dãy số.

b) Tìm số tiền bác An nhận được sau 2 năm.

Lời giải:

a) Ba số hạng đầu của dãy số là

$A_1=200{\left(1+\frac{\mathrm{0,03}}{4}\right)}^1=\mathrm{201,5}$

$A_2=200{\left(1+\frac{\mathrm{0,03}}{4}\right)}^2=\mathrm{203,01125}$

$A_3=200{\left(1+\frac{\mathrm{0,03}}{4}\right)}^3\approx \mathrm{204,5338}$

b) Ta có 2 năm bằng 8 quý, tức là n = 8.

Do đó, sau 2 năm số tiền bác An nhận được là

$A_8=200{\left(1+\frac{\mathrm{0,03}}{4}\right)}^8\approx \mathrm{212,3198}$

Bài 2.9 trang 35 SBT Toán 11 Tập 1: Vi khuẩn E. Coli sinh sản thông qua một quá trình gọi là quá trình phân đôi. Vi khuẩn E. Coli phân chia làm đôi cứ sau 20 phút. Giả sử tốc độ phân chia này được duy trì trong 12 giờ kể từ khi vi khuẩn ban đầu xâm nhập vào cơ thể. Hỏi sau 12 giờ sẽ có bao nhiêu vi khuẩn E. Coli trong cơ thể? Giả sử có một nguồn dinh dưỡng vô hạn để vi khuẩn E. Coli duy trì tốc độ phân chia như cũ trong 48 giờ kể từ khi vi khuẩn ban đầu xâm nhập vào cơ thể. Hỏi sau 48 giờ sẽ có bao nhiêu vi khuẩn E. Coli trong cơ thể?

Lời giải:

Giả sử ban đầu có 1 vi khuẩn E. Coli.

Sau 20 phút lần một, số vi khuẩn là 1 . 2 = 2 (con).

Sau 20 phút lần hai, số vi khuẩn là 2 . 2 = 2² (con).

Sau 20 phút lần ba, số vi khuẩn là 2² . 2 = 2³ (con).

Sau 20 phút lần bốn, số vi khuẩn là 2³ . 2 = 2⁴ (con).

...

Tương tự như vậy sau 12 giờ (bằng 3 . 12 lần 20 phút) thì số vi khuẩn là

2^{3 . 12} = 2³⁶ ≈ 6,87 . 10¹⁰ (con).

Sau 48 giờ (bằng 3 . 48 lần 20 phút) thì số vi khuẩn là

2^{3 . 48} = 2¹⁴⁴ ≈ 2,23 . 10⁴³ (con).

Bài 2.10 trang 35 SBT Toán 11 Tập 1: Một công ty dược phẩm đang thử nghiệm một loại thuốc mới. Một thí nghiệm bắt đầu với 1,0 × 10⁹ vi khuẩn. Một liều thuốc được sử dụng sau mỗi bốn giờ có thể tiêu diệt 4,0 × 10⁸ vi khuẩn. Giữa các liều thuốc, số lượng vi khuẩn tăng lên 25%.

a) Viết hệ thức truy hồi cho số lượng vi khuẩn sống trước mỗi lần sử dụng thuốc.

b) Tìm số vi khuẩn còn sống trước lần sử dụng thuốc thứ năm.

Lời giải:

a) Gọi u₁ = 1,0 . 10⁹ là số vi khuẩn tại thời điểm ban đầu và u_n là số vi khuẩn trước lần dùng thuốc thứ n.

Do mỗi liều thuốc được sử dụng sau bốn giờ có thể tiêu diệt 4,0 . 10⁸ vi khuẩn và giữa các liều thuốc, số lượng vi khuẩn tăng lên 25% nên ta có

u_{n + 1} = (u_n – 4,0 . 10⁸) + 25% . u_n = 1,25u_n – 4,0 . 10⁸.

Ta có hệ thức truy hồi u₁ = 1,0 . 10⁹; u_{n + 1} = 1,25u_n – 4,0 . 10⁸.

b) Ta tính u₅ như sau:

u₁ = 1,0 . 10⁹;

u₂ = 1,25u₁ – 4,0 . 10⁸ = 1,25 . 1,0 . 10⁹ – 4,0 . 10⁸ = 8,5 . 10⁸;

u₃ = 1,25u₂ – 4,0 . 10⁸ = 1, 25 . 8,5 . 10⁸ – 4,0 . 10⁸ = 6,625 . 10⁸;

u₄ = 1,25u₃ – 4,0 . 10⁸ = 1,25 . 6,625 . 10⁸ – 4,0 . 10⁸ = 4,28125 . 10⁸;

u₅ = 1,25u₄ – 4,0 . 10⁸ = 1,25 . 4,28125 . 10⁸ – 4,0 . 10⁸ = 1,3515625 . 10⁸ = 135 156 250;

Vậy số vi khuẩn còn sống trước lần sử dụng thuốc thứ năm là 135 156 250 con.

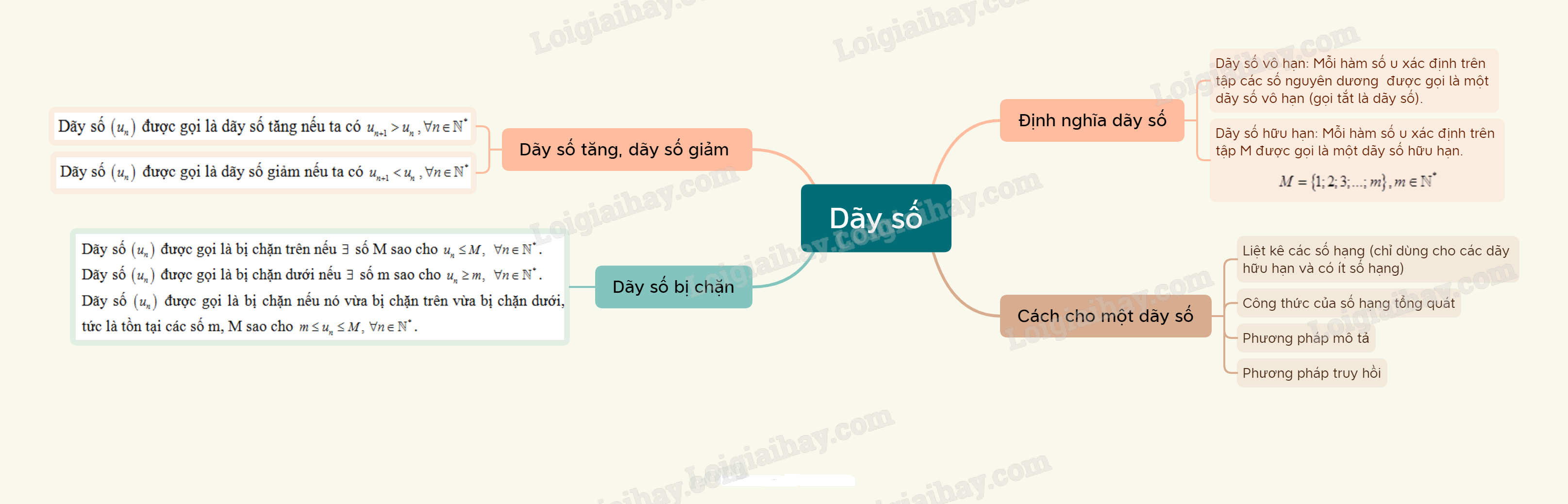
Lý thuyết Dãy số

1. Định nghĩa dãy số

• Dãy số vô hạn

Mỗi hàm số u xác định trên tập các số nguyên dương ${\mathbb{N}}^{\ast }$được gọi là một dãy số vô hạn (gọi tắt là dãy số). Kí hiệu là $u=u\left(n\right)$.

Ta thường viết $u_n$thay cho $u\left(n\right)$ và kí hiệu dãy số $u=u\left(n\right)$bởi $u\left(n\right)$, do đó dãy số $\left(u_n\right)$được viết dưới dạng khai triển $u_1,u_2,u_3,...,u_n,...$

Số $u_1$ là số hạng đầu; $u_n$là số hạng thứ n và gọi là số hạng tổng quát của dãy số.

*Chú ý: Nếu $\mathrm{\forall }n\in {\mathbb{N}}^{\ast },u_n=c$thì $\left(u_n\right)$được gọi là dãy số không đổi.

• Dãy số hữu hạn

Mỗi hàm số u xác định trên tập $M=\left\{1;2;3;...;m\right\},m\in {\mathbb{N}}^{\ast }$ được gọi là một dãy số hữu hạn.

Dạng khai triển của dãy số hữu hạn là $u_1,u_2,u_3,...,u_m$.

Số $u_1$ gọi là số hạng đầu, $u_m$là số hạng cuối.

2. Cách cho một dãy số

Một dãy số có thể cho bằng:

+) Liệt kê các số hạng (chỉ dùng cho các dãy hữu hạn và có ít số hạng).

+) Công thức của số hạng tổng quát.

+) Phương pháp mô tả.

+) Phương pháp truy hồi.

3. Dãy số tăng, dãy số giảm và dãy số bị chặn

Dãy số $\left(u_n\right)$ được gọi là dãy số tăng nếu ta có $u_{n+1}>u_n$$,\mathrm{\forall }n\in {\mathbb{N}}^{\ast }$.

Dãy số $\left(u_n\right)$ được gọi là dãy số giảm nếu ta có $u_{n+1}<u_n$$,\mathrm{\forall }n\in {\mathbb{N}}^{\ast }$.

Dãy số $\left(u_n\right)$ được gọi là bị chặn trên nếu $\mathrm{\exists }$ số M sao cho $u_n\le M,$ $\mathrm{\forall }n\in {\mathbb{N}}^{\ast }$.

Dãy số $\left(u_n\right)$ được gọi là bị chặn dưới nếu $\mathrm{\exists }$ số m sao cho $u_n\ge m,$ $\mathrm{\forall }n\in {\mathbb{N}}^{\ast }$.

Dãy số $\left(u_n\right)$ được gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, tức là tồn tại các số m, M sao cho $m\le u_n\le M,$$\mathrm{\forall }n\in {\mathbb{N}}^{\ast }$.

Xem thêm lời giải SBT Toán 11 sách Kết nối tri thức hay, chi tiết khác:

Bài 6: Cấp số cộng

Bài 7: Cấp số nhân

Bài tập cuối chương 2 trang 40

Bài 8: Mẫu số liệu ghép nhóm

Bài 9: Các số đặc trưng đo xu thế trung tâm