Sách bài tập Toán 11 Bài 19 (Kết nối tri thức): Lôgarit

Giải SBT Toán 11 Bài 19: Lôgarit

Bài 6.11 trang 10 SBT Toán 11 Tập 2: Tính:

a) ${\log }_2\frac{1}{64}$ ; b) log 1 000;

c) log₅1 250 − log₅10; d) $4^{{\log }_{2}3}$ .

Lời giải:

a) ${\log }_2\frac{1}{64}={\log }_2{2}^{-6}=-6$ .

b) log 1 000 = log 10³ = 3.

c) ${\log }_{5}1250-{\log }_{5}10={\log }_5\frac{1250}{10}={\log }_{5}125={\log }_5{5}^3=3$ .

d) $4^{{\log }_{2}3}={\left(2^{{\log }_{2}3}\right)}^2=3^2=9$ .

Bài 6.12 trang 10 SBT Toán 11 Tập 2: Chứng minh rằng:

a) ${\log }_a\left(x+\sqrt{x^2-1}\right)+{\log }_a\left(x-\sqrt{x^2-1}\right)=0$ ;

b) ln (1 + e^2x) = 2x + ln (1 + e^−2x).

Lời giải:

a) Ta có ${\log }_a\left(x+\sqrt{x^2-1}\right)+{\log }_a\left(x-\sqrt{x^2-1}\right)$

$={\log }_{\mathrm{a}}\left[\left(\mathrm{x}+\sqrt{{\mathrm{x}}^2-1}\right)\left(\mathrm{x}-\sqrt{{\mathrm{x}}^2-1}\right)\right]$

$={\log }_{\mathrm{a}}\left[{\mathrm{x}}^2-\left({\mathrm{x}}^2-1\right)\right]={\log }_{\mathrm{a}}1=0$

Vậy ${\log }_a\left(x+\sqrt{x^2-1}\right)+{\log }_a\left(x-\sqrt{x^2-1}\right)=0$ .

b) Ta có ln (1 + e^2x) = ln [e^2x(1 + e^−2x)] = ln e^2x + ln (1 + e^−2x) = 2x + ln (1 + e^−2x).

Vậy ln (1 + e^2x) = 2x + ln (1 + e^−2x).

Bài 6.13 trang 10 SBT Toán 11 Tập 2: Biết log₂3 $\approx$ 1,585. Hãy tính:

a) log₂ 48; b) log₄ 27.

Lời giải:

a) log₂ 48 = log₂ (2⁴×3) = log₂ 2⁴ + log₂ 3

= 4 + log₂ 3 $\approx$ 4 + 1,585 = 5,585.

b)

$$\begin{gathered} {\log }_{4}27=\frac{{\log }_{2}27}{{\log }_{2}4}=\frac{{\log }_2{3}^3}{{\log }_2{2}^2}=\frac{3{\log }_{2}3}{2} \\ =\frac{3}{2}\cdot {\log }_{2}3\approx \frac{3}{2}\cdot 1,585=2,3775 \end{gathered}$$

Bài 6.14 trang 10 SBT Toán 11 Tập 2: Đặt a = log₃ 5, b = log₄ 5. Hãy biểu diễn log₁₅ 10 theo a và b.

Lời giải:

Ta có ${\log }_{15}10=\frac{{\log }_{5}10}{{\log }_{5}15}=\frac{{\log }_5\left(2\cdot 5\right)}{{\log }_5\left(3.5\right)}$$=\frac{{\log }_{5}2+{\log }_{5}5}{{\log }_{5}3+{\log }_{5}5}=\frac{{\log }_{5}2+1}{{\log }_{5}3+1}$

Vì a = log₃ 5 nên ${\log }_{5}3=\frac{1}{a}$ và b = log₄ 5 nên ${\log }_{5}4=\frac{1}{b}$$\iff 2{\log }_{5}2=\frac{1}{b}$ hay ${\log }_{5}2=\frac{1}{2b}$

Do đó ${\log }_{15}10=\frac{{\log }_{5}2+1}{{\log }_{5}3+1}=\frac{\frac{1}{2b}+1}{\frac{1}{a}+1}=\frac{\left(1+2b\right)a}{2b\left(a+1\right)}$ .

Bài 6.15 trang 10 SBT Toán 11 Tập 2: Tìm log₄₉ 32, biết log₂ 14 = a.

Lời giải:

Có ${\log }_{49}32=\frac{{\log }_{2}32}{{\log }_{2}49}=\frac{{\log }_2{2}^5}{{\log }_2{7}^2}=\frac{5}{2{\log }_{2}7}$

Mà log₂ 14 = log₂ (2.7) = log₂ 2 + log₂ 7 = 1 + log₂ 7 = a. Do đó log₂ 7 = a – 1.

Vậy ${\log }_{49}32=\frac{5}{2\left(a-1\right)}$ .

Bài 6.16 trang 10 SBT Toán 11 Tập 2: So sánh các số sau:

a) log₃ 4 và ${\log }_4\frac{1}{3}$; b) $2^{{\log }_{6}3}$ và $3^{{\log }_6\frac{1}{2}}$.

Lời giải:

a) Ta có log₃ 4 > log₃ 3 = 1; ${\log }_4\frac{1}{3}<{\log }_{4}4=1$ nên ${\log }_4\frac{1}{3}<{\log }_{3}4$.

b) Có $2^{{\log }_{6}3}=3^{{\log }_{6}2}$

(do ${\log }_2{2}^{{\log }_{6}3}={\log }_2{3}^{{\log }_{6}2}$$\iff {\log }_{6}3\cdot {\log }_{2}2={\log }_{6}2\cdot {\log }_{2}3$$\iff {\log }_{2}3=\frac{{\log }_{6}3}{{\log }_{6}2}$)

Vì ${\log }_{6}2>{\log }_6\frac{1}{2}$ nên $3^{{\log }_{6}2}>3^{{\log }_6\frac{1}{2}}$hay $2^{{\log }_{6}3}>3^{{\log }_6\frac{1}{2}}$ .

Bài 6.17 trang 10 SBT Toán 11 Tập 2: Biết rằng số chữ số của một số nguyên dương N viết trong hệ thập phân được cho bởi công thức [log N] + 1, ở đó [log N] là phần nguyên của số thực dương logN. Tìm số các chữ số của 2^{2 023} khi viết trong hệ thập phân.

Lời giải:

Có N = 2^{2 023}

Số chữ số của N = 2^{2 023} là: [log 2^{2 023}] + 1 = [2 023.log 2] + 1 = 609.

Vậy số các chữ số của 2^{2 023} là 609.

Bài 6.18 trang 10 SBT Toán 11 Tập 2: Khi gửi tiết kiệm P (đồng) theo thể thức trả lãi kép định kì với lãi suất mỗi kì là r (r cho dưới dạng số thập phân) thì số tiền A (cả vốn lẫn lãi) nhận được sau t kì gửi là A = P(1 + r)^t (đồng). Tính thời gian gửi tiết kiệm cần thiết để số tiền ban đầu tăng gấp đôi.

Lời giải:

Để số tiền tăng gấp đôi tức là A = 2P

Thời gian gửi tiết kiệm để số tiền ban đầu tăng gấp đôi là: 2P = P(1 + r)^t $\iff$ 2 = (1 + r)^t $\iff$ t = log_{1 + r} 2 (năm).

Vậy cần log_{1 + r} 2 năm gửi tiết kiệm để số tiền ban đầu tăng gấp đôi.

Bài 6.19 trang 11 SBT Toán 11 Tập 2: Một người gửi tiết kiệm 100 triệu đồng vào ngân hàng theo thể thức lãi kép kì hạn 6 tháng với lãi suất 8% một năm. Giả sử lãi suất không thay đổi. Hỏi sau bao lâu người đó nhận được ít nhất 120 triệu đồng?

Lời giải:

Vì lãi suất 8% một năm nên lãi suất kì hạn 6 tháng sẽ là r = 4% = 0,04.

Thay P = 100; r = 0,04 và A = 120 vào công thức A = P(1 + r)^t , ta được:

120 = 100(1 + 0,04)^t $\iff$ 1,2 = 1,04^t $\iff$ t = log_1,04 1,2 $\approx$ 4,65.

Vậy sau 5 kì gửi tiết kiệm kì hạn 6 tháng, tức là sau 30 tháng, người đó sẽ nhận được ít nhất 120 triệu đồng.

Bài 6.20 trang 11 SBT Toán 11 Tập 2: Nồng độ cồn trong máu (BAC) là chỉ số dùng để đo lượng cồn trong máu của một người. Chẳng hạn, BAC 0,02% hay 0,2mg/ml, nghĩa là có 0,02 g cồn trong 100 ml máu. Nếu một người với BAC bằng 0,02% có nguy cơ bị tai nạn ô tô cao gấp 1,4 lần so với một người không uống rượu, thì nguy cơ tương đối của tai nạn với BAC 0,02% là 1,4. Nghiên cứu y tế gần đây cho thấy rằng nguy cơ tương đối của việc gặp tai nạn khi đang lái ô tô có thể được mô hình hóa bằng một phương trình có dạng

R = e^kx,

trong đó x (%) là nồng độ cồn trong máu và k là một hằng số.

a) Nghiên cứu chỉ ra rằng nguy cơ tương đối của một người bị tai nạn với BAC bằng 0,02% là 1,4. Tìm hằng số k trong phương trình.

b) Nguy cơ tương đối là bao nhiêu nếu nồng độ cồn trong máu là 0,17%?

c) Tìm BAC tương ứng với nguy cơ tương đối là 100.

d) Giả sử nếu một người có nguy cơ tương đối từ 5 trở lên sẽ không được phép lái xe, thì một người có nồng độ cồn trong máu từ bao nhiêu trở lên sẽ không được phép lái xe?

Lời giải:

a) Theo đề có nguy cơ tương đối của một người bị tai nạn với BAC bằng 0,02% là 1,4 nên x = 0,02% và R = 1,4.

Thay x = 0,02% và R = 1,4 vào phương trình R = e^kx ta được $1,4=e^{k\cdot \frac{0,02}{100}}$ $\iff k\cdot \frac{0,02}{100}=\ln 1,4\iff k\approx 1682,36$ .

Vậy hệ số k trong phương trình khoảng 1 682, 36.

b) Với x = 0,17% và k =1 682, 36 thì nguy cơ tương đối là: $R=e^{1682,36\cdot \frac{0,17}{100}}\approx 17,46$ .

Vậy nếu nồng độ cồn trong máu là 0,17% thì nguy cơ tương đối khoảng 17,46.

c) Có nguy cơ tương đối là 100 tức R = 100.

Ta có 100 = e^{1 682,36x} $\iff$ 1 682,36x = ln 100 $\iff$ x $\approx$ 0,27%.

Vậy BAC khoảng 0,27%.

d) Nếu một người có nguy cơ tương đối từ 5 trở lên sẽ không được phép lái xe tức là R ≥ 5. Khi đó, ta có e^{1 682,36x} ≥ 5 hay x ≥ 0,096%.

Vậy một người có nồng độ cồn trong máu khoảng 0,096% trở lên sẽ không được phép lái xe.

Lý thuyết Lôgarit

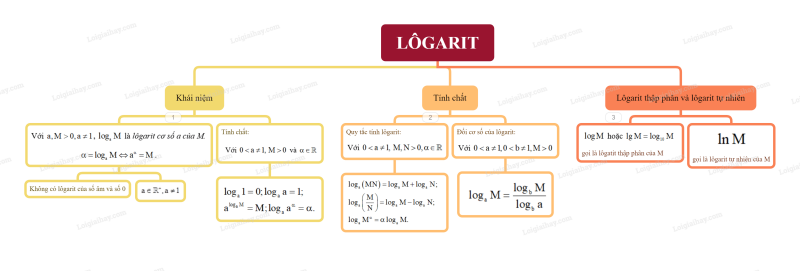
1. Khái niệm Lôgarit

Cho a là một số thực dương khác 1 và M là một số thực dương. Số thực $\alpha$ để $a^{\alpha }=M$ được gọi là lôgarit cơ số a của M và kí hiệu là ${\log }_{a}M$.

$\alpha ={\log }_{a}M\iff a^{\alpha }=M$.

Chú ý: Không có lôgarit của số âm và số 0. Cơ số của lôgarit phải dương và khác 1. Từ định nghĩa lôgarit, ta có các tính chất sau:

Với $0<a\ne 1,M>0$ và $\alpha$ là số thực tùy ý, ta có:

$\begin{array}{l}{\log }_{a}1=0;{\log }_{a}a=1;\\ a^{{\log }_{a}M}=M;{\log }_a{a}^{\alpha }=\alpha .\end{array}$

2. Tính chất của lôgarit

a) Quy tắc tính lôgarit

Giả sử a là số thực dương khác 1, M và N là các số thực dương, $\alpha$ là số thực tùy ý. Khi đó:

$\begin{array}{l}{\log }_a\left(MN\right)={\log }_{a}M+{\log }_{a}N;\\ {\log }_a\left(\frac{M}{N}\right)={\log }_{a}M-{\log }_{a}N;\\ {\log }_a{M}^{\alpha }=\alpha {\log }_{a}M.\end{array}$

b) Đổi cơ số của lôgarit

Với các cơ số lôgarit a và b bất kì ($0<a\ne 1,0<b\ne 1$) và M là số thực dương tùy ý, ta luôn có:

${\log }_{a}M=\frac{{\log }_{b}M}{{\log }_{b}a}$.

3. Lôgarit thập phân và lôgarit tự nhiên

a) Lôgarit thập phân

Lôgarit cơ số 10 của một số dương M gọi là lôgatit thập phân của M, kí hiệu là $\log M$ hoặc $\lg M$ (đọc là lốc của M).

b) Số e và lôgarit tự nhiên

Lôgarit cơ số e của một số dương M gọi là lôgarit tự nhiên của M, kí hiệu là $\ln M$ (đọc là lôgarit Nêpe của M).

Sơ đồ tư duy Lôgarit

Xem thêm lời giải SBT Toán 11 sách Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 5 trang 87

Bài 18: Lũy thừa với số mũ thực

Bài 20: Hàm số mũ và hàm số lôgarit

Bài 21: Phương trình, bất phương trình mũ và lôgarit

Bài tập cuối chương 6 trang 20