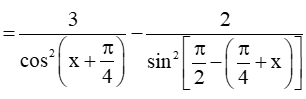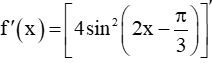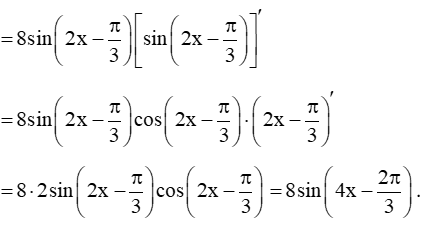Sách bài tập Toán 11 Bài 32 (Kết nối tri thức): Các quy tắc tính đạo hàm
Với giải sách bài tập Toán 11 Bài 32: Các quy tắc tính đạo hàm sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 11 Bài 32.
Giải SBT Toán 11 Bài 32: Các quy tắc tính đạo hàm
Bài 9.8 trang 60 SBT Toán 11 Tập 2: Tính đạo hàm của các hàm số sau:
Lời giải:
a) Ta có: y' = ((x + 1)2)'(x2 – 1) + (x + 1)2(x2 – 1)'
= 2(x + 1)(x2 – 1) + 2x(x + 1)2
= 2x3 – 2x + 2x2 – 2 + 2x3 + 4x2 + 2x = 4x3 + 6x2 – 2.
Vậy y' = 4x3 + 6x2 – 2.
b) y'
.
Bài 9.9 trang 60 SBT Toán 11 Tập 2: Tính đạo hàm của các hàm số sau:
b) .
Lời giải:
a)
.
Vậy .
b)
.
Bài 9.10 trang 60 SBT Toán 11 Tập 2: Cho hàm số và . Tính f'(0) – g'(1).
Lời giải:
Có
.
Khi đó .
Có .
Khi đó .
Do đó f'(0) – g'(1) = . Vậy f'(0) – g'(1) = 0.
Bài 9.11 trang 60 SBT Toán 11 Tập 2: Tính đạo hàm của hàm số .
Lời giải:
Có
Có
= -sin2x + 2cossin2x = -sin2x + sin2x = 0.
Vậy f'(x) = 0 với mọi x ℝ.
Lời giải:
+ Có
Vì 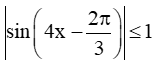
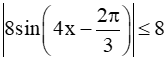
Vậy |f'(x)| ≤ 8 với mọi x ℝ.
+ Có f'(x) = 8 8sin=8
(k ℤ)
(k ℤ)
(k ℤ).
Vậy f'(x) = 8 khi với k ℤ.
Lời giải:
Đạo hàm hai vế của phương trình đã cho, ta có
(xy)' = (1 + lny)' y + xy' =
y = - xy' y = y'.
y = y' y' = .
Tại x = 0 thay vào phương trình xy = 1 + lny ta được lny = −1 y = e−1.
Do đó .
Vậy .
Lời giải:
Vận tốc của vật tại thời điểm t là v(t) = h'(t) = = vo - gt.
Tại thời điểm vật chạm đất thì h = 0 (t > 0) tức là vot - gt2 = 0
.
Vận tốc khi vật chạm đất là (m/s).
Vậy vận tốc khi vật chạm đất là −v0 m/s.
Lời giải:
Vận tốc của hạt sau t giây là v(t) = s'(t) =
.
Vì 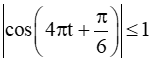
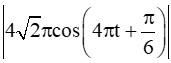
Do đó vận tốc cực đại của hạt là 417,8 m/s đạt được khi 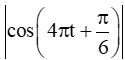
, với k ℕ*.
Vậy vận tốc cực đại của hạt khoảng 17,8 m/s khi ,với k ℕ*.
Lý thuyết Các quy tắc tính đạo hàm
1. Đạo hàm của tổng, hiệu, tích, thương
Giả sử u = u(x), v = v(x) là các hàm số có đạo hàm tại điểm x thuộc khoảng (a; b). Khi đó
(k là hằng số);
.
2. Đạo hàm của hàm hợp
Nếu hàm số u = g(x) có đạo hàm tại x là và hàm số y = f(u) có đạo hàm tại u là thì hàm hợp y = f(g(x)) có đạo hàm tại x là .
3. Bảng đạo hàm của một số hàm số sơ cấp cơ bản và hàm hợp

Sơ đồ tư duy Các quy tắc tính đạo hàm
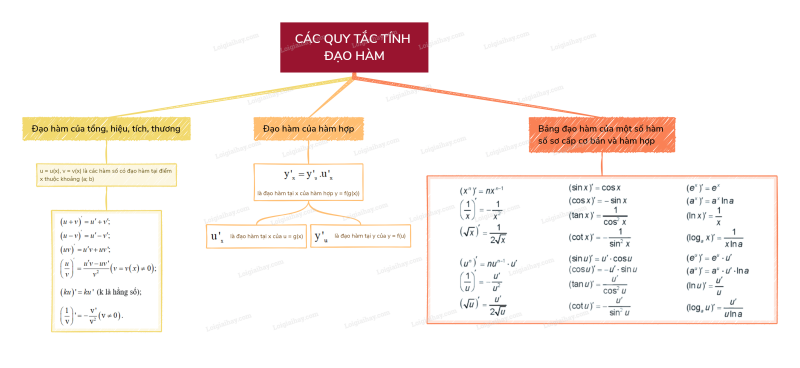
Xem thêm lời giải SBT Toán 11 sách Kết nối tri thức hay, chi tiết khác:
Bài 30: Công thức nhân xác suất cho hai biến cố độc lập
Xem thêm các chương trình khác:
- Soạn văn lớp 11 Kết nối tri thức - hay nhất
- Văn mẫu lớp 11 - Kết nối tri thức
- Tóm tắt tác phẩm Ngữ văn 11 – Kết nối tri thức
- Tác giả tác phẩm Ngữ văn 11 - Kết nối tri thức
- Giải SBT Ngữ văn 11 – Kết nối tri thức
- Bố cục tác phẩm Ngữ văn 11 – Kết nối tri thức
- Giải Chuyên đề học tập Ngữ văn 11 – Kết nối tri thức
- Nội dung chính tác phẩm Ngữ văn lớp 11 – Kết nối tri thức
- Soạn văn 11 Kết nối tri thức (ngắn nhất)
- Bài tập Tiếng Anh 11 Global success theo Unit có đáp án
- Giải sgk Tiếng Anh 11 – Global success
- Giải sbt Tiếng Anh 11 - Global Success
- Trọn bộ Từ vựng Tiếng Anh 11 Global success đầy đủ nhất
- Ngữ pháp Tiếng Anh 11 Global success
- Giải sgk Vật lí 11 – Kết nối tri thức
- Lý thuyết Vật lí 11 – Kết nối tri thức
- Giải sbt Vật lí 11 – Kết nối tri thức
- Giải Chuyên đề học tập Vật lí 11 – Kết nối tri thức
- Chuyên đề dạy thêm Vật lí 11 cả 3 sách (2024 có đáp án)
- Giải sgk Hóa học 11 – Kết nối tri thức
- Giải Chuyên đề học tập Hóa học 11 – Kết nối tri thức
- Lý thuyết Hóa 11 - Kết nối tri thức
- Giải sbt Hóa học 11 – Kết nối tri thức
- Chuyên đề dạy thêm Hóa 11 cả 3 sách (2024 có đáp án)
- Giải sgk Sinh học 11 – Kết nối tri thức
- Lý thuyết Sinh học 11 – Kết nối tri thức
- Giải Chuyên đề học tập Sinh học 11 – Kết nối tri thức
- Giải sbt Sinh học 11 – Kết nối tri thức
- Giải sgk Giáo dục Kinh tế và Pháp luật 11 – Kết nối tri thức
- Giải Chuyên đề học tập Kinh tế pháp luật 11 – Kết nối tri thức
- Lý thuyết Kinh tế pháp luật 11 – Kết nối tri thức
- Giải sbt Kinh tế pháp luật 11 – Kết nối tri thức
- Giải sgk Lịch sử 11 – Kết nối tri thức
- Giải Chuyên đề học tập Lịch sử 11 – Kết nối tri thức
- Lý thuyết Lịch sử 11 - Kết nối tri thức
- Giải sbt Lịch sử 11 – Kết nối tri thức
- Giải sgk Địa lí 11 – Kết nối tri thức
- Giải Chuyên đề học tập Địa lí 11 – Kết nối tri thức
- Lý thuyết Địa lí 11 - Kết nối tri thức
- Giải sbt Địa lí 11 – Kết nối tri thức
- Giải sgk Công nghệ 11 – Kết nối tri thức
- Lý thuyết Công nghệ 11 - Kết nối tri thức
- Giải sbt Công nghệ 11 – Kết nối tri thức
- Giải sgk Tin học 11 – Kết nối tri thức
- Giải Chuyên đề học tập Tin học 11 – Kết nối tri thức
- Lý thuyết Tin học 11 - Kết nối tri thức
- Giải sbt Tin học 11 – Kết nối tri thức
- Giải sgk Giáo dục quốc phòng an ninh 11 – Kết nối tri thức
- Lý thuyết Giáo dục quốc phòng 11 – Kết nối tri thức
- Giải sbt Giáo dục quốc phòng 11 – Kết nối tri thức
- Giải sgk Hoạt động trải nghiệm 11 – Kết nối tri thức