Sách bài tập Toán 11 Bài 21 (Kết nối tri thức): Phương trình, bất phương trình mũ và lôgarit

Giải SBT Toán 11 Bài 21: Phương trình, bất phương trình mũ và lôgarit

Bài 6.31 trang 19 SBT Toán 11 Tập 2: Giải các phương trình mũ sau:

a) 4^{2x – 1} = 8^{x + 3}; b) $9^{2x}\cdot {27}^{x^2}=\frac{1}{3}$ ;

c) ${\left(e^4\right)}^x\cdot e^{x^2}=e^{12}$ ; d) 5^{2x – 1} = 20.

Lời giải:

a) Ta có: 4^{2x – 1} = 8^{x + 3} $\iff$ 2^{2(2x – 1)} = 2^{3(x + 3)}

$\iff$ 2(2x – 1) = 3(x + 3) $\iff$ 4x – 2 = 3x + 9 $\iff$ x = 11.

Vậy phương trình có nghiệm là x = 11.

b) Ta có:

$$\begin{gathered} 9^{2x}\cdot {27}^{x^2}=\frac{1}{3}\iff 3^{4x}\cdot 3^{3x^2}=3^{-1} \\ \iff 3^{3x^2+4x}=3^{-1}\iff 3x^2+4x=-1 \end{gathered}$$

$\iff 3x^2+4x+1=0\iff \left(3x+1\right)\left(x+1\right)=0\iff \left[\begin{array}{l}x=-\frac{1}{3}\\ x=-1\end{array}\right.$.

Vậy tập nghiệm của phương trình là $S=\left\{-\frac{1}{3};-1\right\}$ .

c) Ta có:

${\left(e^4\right)}^x\cdot e^{x^2}=e^{12}\iff e^{4x}\cdot e^{x^2}=e^{12}\iff e^{x^2+4x}=e^{12}\iff x^2+4x=12$

$\iff x^2+4x-12=0\iff \left(x-2\right)\left(x+6\right)=0\iff \left[\begin{array}{l}x=2\\ x=-6\end{array}\right.$.

Vậy tập nghiệm của phương trình là S = {−6; 2}.

d) 5^{2x – 1} = 20 $\iff$ 2x – 1 = log₅ 20 $\iff$ 2x = log₅ 20 + 1 $\iff$ $x=\frac{1}{2}\left({\log }_{5}20+1\right)$.

Vậy nghiệm của phương trình là $x=\frac{1}{2}\left({\log }_{5}20+1\right)$ .

Bài 6.32 trang 19 SBT Toán 11 Tập 2: Giải các phương trình lôgarit sau:

a) log₃ (4x – 1) = 2; b) log₂ (x² – 1) = log₂ (3x + 3);

c) log_x 81 = 2; d) log₂ 8^x = −3.

Lời giải:

a) Điều kiện: 4x – 1 > 0 $\iff x>\frac{1}{4}$ .

Ta có: log₃ (4x – 1) = 2 $\iff$ 4x – 1 = 3² $\iff$ 4x – 1 = 9 $\iff$ 4x = 10 $\iff x=\frac{5}{2}$(thỏa mãn điều kiện).

Vậy nghiệm của phương trình là $x=\frac{5}{2}$ .

b) Điều kiện:

$$\begin{gathered} \left\{\begin{array}{l}{x}^2-1>0\\ 3x+3>0\end{array}\right.\iff \left\{\begin{array}{l}\left(x-1\right)\left(x+1\right)>0\\ x+1>0\end{array}\right. \\ \iff \left\{\begin{array}{l}x-1>0\\ x+1>0\end{array}\right.\iff \left\{\begin{array}{l}x>1\\ x>-1\end{array}\right.\iff x>1 \end{gathered}$$

Ta có: log₂ (x² – 1) = log₂ (3x + 3) $\iff$ x² – 1 = 3x + 3 $\iff$ x² – 3x – 4 = 0

$\iff$ (x + 1)(x – 4) = 0 $\iff$ x = −1 (loại) hoặc x = 4 (thỏa mãn).

Vậy nghiệm của phương trình là x = 4.

c) Điều kiện: 0 < x ≠ 1.

Ta có: log_x 81 = 2 $\iff$ 81 = x² $\iff$ x = 9 (thỏa mãn) hoặc x = −9 (loại).

Vậy nghiệm của phương trình là x = 9.

d) Ta có: log₂ 8^x = −3 $\iff$ 8^x = 2⁻³ $\iff$ 2^3x = 2⁻³ $\iff$ 3x = −3 $\iff$x = −1.

Vậy nghiệm của phương trình là x = −1.

Bài 6.33 trang 19 SBT Toán 11 Tập 2: Giải các bất phương trình mũ sau:

a) $2^{2x-3}>\frac{1}{4}$ ; b) ${\left(\frac{1}{2}\right)}^{x^2}\ge {\left(\frac{1}{2}\right)}^{5x-6}$ ;

c) 25^x ≤ 5^{4x − 3} ; d) 9^x – 3^x – 6 ≤ 0.

Lời giải:

a) $2^{2x-3}>\frac{1}{4}\iff 2^{2x-3}>2^{-2}$$\iff 2x-3>-2\iff 2x>1\iff x>\frac{1}{2}$

Vậy nghiệm của bất phương trình là $x>\frac{1}{2}$ .

b)${\left(\frac{1}{2}\right)}^{x^2}\ge {\left(\frac{1}{2}\right)}^{5x-6}\iff x^2\le 5x-6$$\iff x^2-5x+6\le 0\iff \left(x-2\right)\left(x-3\right)\le 0$

$\iff 2\le x\le 3.$

Vậy tập nghiệm của bất phương trình là [2; 3].

c) 25^x ≤ 5^{4x − 3} $\iff$ 5^2x ≤ 5^{4x − 3} $\iff$ 2x ≤ 4x – 3 $\iff$ 2x ≥ 3 $\iff$ x ≥ 1,5.

Vậy tập nghiệm của bất phương trình là [1,5; +$\infty$).

d) Đặt 3^x = t (t > 0).

Khi đó bất phương trình trở thành t² – t – 6 ≤ 0 $\iff$ (t – 3)(t + 2) ≤ 0 $\iff$ −2 ≤ t ≤ 3.

Mà t > 0 nên ta có 0 < t ≤ 3.

Khi đó, ta có 3^x ≤ 3 $\iff$ x ≤ 1.

Vậy tập nghiệm của bất phương trình là (−$\infty$; 1].

Bài 6.34 trang 19 SBT Toán 11 Tập 2: Giải các bất phương trình lôgarit sau:

a) log₃ (2x + 1) ≥ 2; b) log₂ (3x – 1) < log₂ (9 – 2x);

c) ${\log }_{\frac{1}{2}}\left(x+1\right)\le {\log }_{\frac{1}{2}}\left(4x-5\right)$; d) log₂ (2x – 1) ≤ log₄ (x + 1)².

Lời giải:

a) Điều kiện $2x+1>0\iff x>-\frac{1}{2}$ .

Ta có log₃ (2x + 1) ≥ 2 $\iff$ 2x + 1 ≥ 3² $\iff$ 2x + 1 ≥ 9 $\iff$ 2x ≥ 8 $\iff$ x ≥ 4.

Kết hợp với điều kiện, ta được x ≥ 4.

Vậy tập nghiệm của bất phương trình là [4; +$\infty$).

b) Điều kiện $\left\{\begin{array}{l}3x-1>0\\ 9-2x>0\end{array}\right.\iff \left\{\begin{array}{l}x>\frac{1}{3}\\ x<\frac{9}{2}\end{array}\right.\iff \frac{1}{3}<x<\frac{9}{2}$ .

Ta có:

log₂ (3x – 1) < log₂ (9 – 2x)

$\iff$ 3x – 1 < 9 – 2x

$\iff$ 3x + 2x < 9 + 1

$\iff$ 5x < 10 $\iff$ x < 2.

Kết hợp với điều kiện, ta được $\frac{1}{3}<x<2$ .

Vậy tập nghiệm của bất phương trình là $\left(\frac{1}{3};2\right)$ .

c) Điều kiện: $\left\{\begin{array}{l}x+1>0\\ 4x-5>0\end{array}\right.\iff \left\{\begin{array}{l}x>-1\\ x>\frac{5}{4}\end{array}\right.\iff x>\frac{5}{4}$ .

Ta có:

${\log }_{\frac{1}{2}}\left(x+1\right)\le {\log }_{\frac{1}{2}}\left(4x-5\right)$

$\iff x+1\ge 4x-5\iff 3x\le 6\iff x\le 2$ .

Kết hợp điều kiện, ta có: $\frac{5}{4}<x\le 2$ .

Vậy tập nghiệm của bất phương trình là $\left(\frac{5}{4};2\right]$ .

d) Điều kiện: $\left\{\begin{array}{l}2x-1>0\\ {\left(x+1\right)}^2>0\end{array}\right.\iff \left\{\begin{array}{l}x>\frac{1}{2}\\ x\ne -1\end{array}\right.\iff x>\frac{1}{2}$.

Ta có:

$$\begin{gathered} {\log }_2\left(2x-1\right)\le {\log }_4{\left(x+1\right)}^2 \\ \iff {\log }_2\left(2x-1\right)\le \frac{{\log }_2{\left(x+1\right)}^2}{{\log }_{2}4} \end{gathered}$$

$$\begin{gathered} \iff {\log }_2\left(2x-1\right)\le \frac{{\log }_2{\left(x+1\right)}^2}{2} \\ \iff 2{\log }_2\left(2x-1\right)\le {\log }_2{\left(x+1\right)}^2 \end{gathered}$$

$\iff {\log }_2{\left(2x-1\right)}^2\le {\log }_2{\left(x+1\right)}^2$

$$\begin{gathered} \iff {\left(2x-1\right)}^2\le {\left(x+1\right)}^2 \\ \iff 4x^2-4x+1\le x^2+2x+1 \end{gathered}$$

$$\begin{gathered} \iff 3x^2-6x\le 0 \\ \iff 3x\left(x-2\right)\le 0 \\ \iff 0\le x\le 2 \end{gathered}$$.

Kết hợp với điều kiện, ta có: $\frac{1}{2}<x\le 2$ .

Vậy tập nghiệm của bất phương trình là $\left(\frac{1}{2};2\right]$ .

Bài 6.35 trang 19 SBT Toán 11 Tập 2: Tìm tập xác định của các hàm số sau:

a) $y=\frac{1}{3^x-9}$ ; b) y = ln (4 – x²);

c) $y=\log \frac{1}{5-x}$ ; d) $y=\frac{2}{{\log }_4\left(x-1\right)}$.

Lời giải:

a) Điều kiện: 3^x – 9 ≠ 0 $\iff$ 3^x ≠ 9 $\iff$ 3^x ≠ 3² $\iff$ x ≠ 2.

Vậy tập xác định của hàm số là ℝ\{2}.

b) Điều kiện: 4 – x² > 0 $\iff$ (2 – x)(2 + x) > 0 $\iff$ −2 < x < 2.

Vậy tập xác định của hàm số là (−2; 2).

c) Điều kiện: $\frac{1}{5-x}>0\iff 5-x>0\iff x<5$.

Vậy tập xác định của hàm số là (−$\infty$; 5).

d) Điều kiện:

$$\begin{gathered} \left\{\begin{array}{l}x-1>0\\ {\log }_4\left(x-1\right)\ne 0\end{array}\right.\iff \left\{\begin{array}{l}x>1\\ {\log }_4\left(x-1\right)\ne {\log }_{4}1\end{array}\right. \\ \iff \left\{\begin{array}{l}x>1\\ x-1\ne 1\end{array}\right.\iff \left\{\begin{array}{l}x>1\\ x\ne 2\end{array}\right. \end{gathered}$$

Vậy tập xác định của hàm số là (1; +$\infty$)\{2}.

Bài 6.36 trang 19 SBT Toán 11 Tập 2: Áp suất khí quyển p lên một vật giảm khi độ cao tăng dần. Giả sử áp suất này (tính bằng milimét thủy ngân) được biểu diễn theo độ cao h (tính bằng kilômét) so với mực nước biển bằng công thức p(h) = 760.e^−0,145h.

a) Một máy bay đang chịu áp suất khí quyển 320 mmHg. Tìm độ cao của máy bay đó.

b) Một người đứng trên đỉnh của một ngọn núi và chịu áp suất khí quyển 667 mmHg. Tìm chiều cao của ngọn núi này.

Lời giải:

a) Một máy bay đang chịu áp suất khí quyển 320 mmHg tức là p = 320 thay vào công thức p(h) = 760.e^−0,145h ta được:

760.e^−0,145h = 320 $\iff$ e^−0,145h = 320 : 760

$\iff e^{-0,145h}=\frac{8}{19}$ $\iff -0,145h=\ln \frac{8}{19}$

$\iff h=\ln \frac{8}{19}:\left(-0,145\right)$$\iff h\approx 5,965$(km).

Vậy máy bay ở độ cao khoảng 5,965 km.

b) Một người đứng trên đỉnh của một ngọn núi và chịu áp suất khí quyển 667 mmHg tức p = 667 thay vào công thức p(h) = 760.e^−0,145h ta được: 760.e^−0,145h = 667

$\iff e^{-0,145h}=\frac{667}{760}$$\iff -0,145h=\ln \frac{667}{760}$

$\iff h=\ln \frac{667}{760}:\left(-0,145\right)$$\iff h\approx 0,9$(km).

Vậy chiều cao của ngọn núi khoảng 0,9 km.

Bài 6.37 trang 19 SBT Toán 11 Tập 2: Giả sử giá trị còn lại V (triệu đồng) của một chiếc ô tô nào đó sau t năm được cho bằng công thức V(t) = 730 . (0,82)^t.

a) Theo mô hình này, khi nào chiếc xe có giá trị 500 triệu đồng?

b) Theo mô hình này, khi nào chiếc xe có giá trị 200 triệu đồng?

(Kết quả của câu a và câu b được tính tròn năm).

Lời giải:

a) Chiếc xe có giá trị 500 triệu đồng tức là V = 500 thay vào công thức

V(t) = 730 . (0,82)^t ta được 500 = 730 . (0,82)^t $\iff$${\left(0,82\right)}^t=\frac{50}{73}$$\iff t={\log }_{0,82}\frac{50}{73}$$\iff t\approx 1,91$ (năm).

Vậy chiếc xe có giá trị 500 triệu đồng sau khoảng 2 năm.

b) Chiếc xe có giá trị 200 triệu đồng tức là V = 200 thay vào công thức

V(t) = 730 . (0,82)^t ta được 200 = 730 . (0,82)^t $\iff {\left(0,82\right)}^t=\frac{20}{73}$$\iff t={\log }_{0,82}\frac{20}{73}$$\iff t\approx 6,52$ (năm).

Vậy chiếc xe có giá trị 200 triệu đồng sau khoảng 7 năm.

Bài 6.38 trang 20 SBT Toán 11 Tập 2: Giả sử tổng chi phí hoạt động (đơn vị tỉ đồng) trong một năm của một công ty được tính bằng công thức C(t) = 90 – 50e^−t, trong đó t là thời gian tính bằng năm kể từ khi công ty được thành lập. Tính chi phí hoạt động của công ty đó vào năm thứ 10 sau khi thành lập (làm tròn kết quả đến chữ số thập phân thứ ba).

Lời giải:

Chi phí hoạt động của công ty đó vào năm thứ 10 là:

C(10) = 90 – 50e⁻¹⁰ $\approx$ 89,998 (tỉ đồng).

Vậy chi phí hoạt động của công ty đó vào năm thứ 10 sau khi thành lập khoảng 89,998 tỉ đồng.

Bài 6.39 trang 20 SBT Toán 11 Tập 2: Nhắc lại rằng độ pH của một dung dịch được tính bằng công thức pH = −log[H⁺], ở đó [H⁺] là nồng độ ion hydrogen của dung dịch tính bằng mol/lít. Biết rằng máu của người bình thường có độ pH từ 7,30 đến 7,45. Hỏi nồng độ ion hydrogen trong máu người bình thường nhận giá trị trong đoạn nào?

Lời giải:

Vì máu của người bình thường có độ pH từ 7,30 đến 7,45 nên 7,30 ≤ −log[H⁺] ≤ 7,45 $\iff$ −7,45 ≤ log[H⁺] ≤ −7,30

$\iff$ 10^−7,45 ≤ [H⁺] ≤ 10^−7,30

$\iff$ 3,55.10⁻⁸ ≤ [H⁺] ≤ 5,01.10⁻⁸.

Vậy nồng độ ion hydrogen trong máu người bình thường nhận giá trị trong đoạn [3,55.10⁻⁸ ; 5,01.10⁻⁸].

Bài 6.40 trang 20 SBT Toán 11 Tập 2: Nhắc lại rằng mức cường độ âm (đo bằng dB) được tính bởi công thức $L=10\log \frac{I}{I_0}$ , trong đó I là cường độ âm tính theo W/m² và I₀ = 10⁻¹² W/m².

a) Tính cường độ âm của âm thanh tàu điện ngầm có mức cường độ âm là 100 dB.

b) Âm thanh trên một tuyến đường giao thông có mức cường độ âm thay đổi từ 70 dB đến 85 dB. Hỏi cường độ âm thay đổi trong đoạn nào?

Lời giải:

a) Âm thanh tàu điện ngầm có mức cường độ âm là 100 dB tức là L = 100 thay vào công thức $L=10\log \frac{I}{I_0}$ ta được:

$100=10\log \frac{I}{{10}^{-12}}$

$\iff 10=\log \frac{I}{{10}^{-12}}$

$\iff \frac{I}{{10}^{-12}}={10}^{10}$

$\iff I={10}^{10}\cdot {10}^{-12}$

$\iff I=0,01$ (W/m²).

Vậy cường độ âm của âm thanh tàu điện ngầm có mức cường độ âm 100 dB là 0,01 W/m².

b) Âm thanh trên một tuyến đường giao thông có mức cường độ âm thay đổi từ 70 dB đến 85 dB tức là $70\le 10\log \frac{I}{{10}^{-12}}\le 85$

$\iff 7\le \log \frac{I}{{10}^{-12}}\le 8,5$$\iff {10}^7\le \frac{I}{{10}^{-12}}\le {10}^{8,5}$

$\iff {10}^7\cdot {10}^{-12}\le I\le {10}^{8,5}\cdot {10}^{-12}$

$\iff {10}^{-5}\le I\le {10}^{-3,5}$ .

Vậy cường độ âm thay đổi trong đoạn [10⁻⁵; 10^−3,5].

Lý thuyết Phương trình, bất phương trình mũ và lôgarit

1. Phương trình mũ

Phương trình mũ cơ bản có dạng $a^x=b$(với $0<a\ne 1$).

- Nếu b > 0 thì phương trình có nghiệm duy nhất $x={\log }_{a}b$.

- Nếu b $\le$ 0 thì phương trình vô nghiệm.

Minh họa bằng đồ thị:

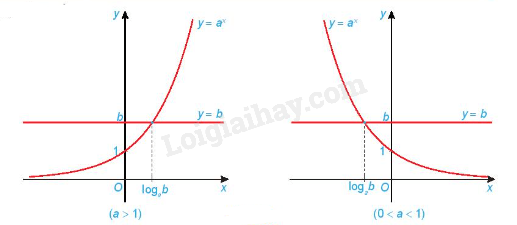
Chú ý: Phương pháp giải phương trình mũ bằng cách đưa về cùng cơ số:

Nếu $0<a\ne 1$ thì $a^u=a^v\iff u=v$.

2. Phương trình lôgarit

Phương trình lôgarit cơ bản có dạng ${\log }_{a}x=b\left(0<a\ne 1\right)$.

Phương trình lôgarit cơ bản ${\log }_{a}x=b$ có nghiệm duy nhất $x=a^b$.

Minh họa bằng đồ thị:

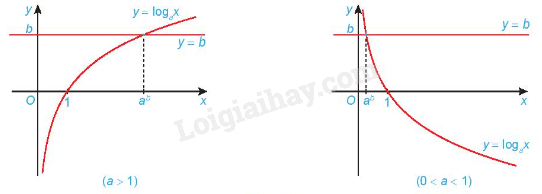
Chú ý: Phương pháp giải phương trình lôgarit bằng cách đưa về cùng cơ số:

Nếu $u,v>0$ và $0<a\ne 1$ thì ${\log }_{a}u={\log }_{a}v\iff u=v$.

3. Bất phương trình mũ

Bất phương trình mũ cơ bản có dạng $a^x>b$ (hoặc $a^x\ge b,a^x<b,a^x\le b$) với $a>0,a\ne 1$.

Xét bất phương trình dạng $a^x>b$:

- Nếu $b\le 0$ thì tập nghiệm của bất phương trình là $\mathbb{R}$.

- Nếu b > 0 thì bất phương trình tương đương với $a^x>a^{{\log }_{a}b}$.

Với a > 1, nghiệm của bất phương trình là $x>{\log }_{a}b$.

Với $0<a<1$, nghiệm của bất phương trình là $x<{\log }_{a}b$.

Chú ý:

a) Các bất phương trình mũ cơ bản còn lại được giải tương tự.

b) Nếu a > 1 thì $a^u=a^v\iff u>v$.

Nếu 0 < a < 1 thì $a^u>a^v\iff u<v$.

4. Bất phương trình lôgarit

Bất phương trình lôgarit cơ bản có dạng ${\log }_{a}x>b$(hoặc ${\log }_{a}x\ge b,{\log }_{a}x<b,{\log }_{a}x\le b$) với $a>0,a\ne 1$.

Xét bất phương trình dạng ${\log }_{a}x>b$:

- Nếu a > 1 thì nghiệm của bất phương trình là $x>a^b$.

- Nếu 0 < a < 1 thì nghiệm của bất phương trình là $0<x<a^b$.

Chú ý:

a) Các bất phương trình lôgarit cơ bản còn lại được giải tương tự.

b) Nếu a > 1 thì ${\log }_{a}u>{\log }_{a}v\iff u>v>0$.

Nếu 0 < a < 1 thì ${\log }_{a}u>{\log }_{a}v\iff 0<u<v$.

Sơ đồ tư duy Phương trình, bất phương trình mũ và lôgarit

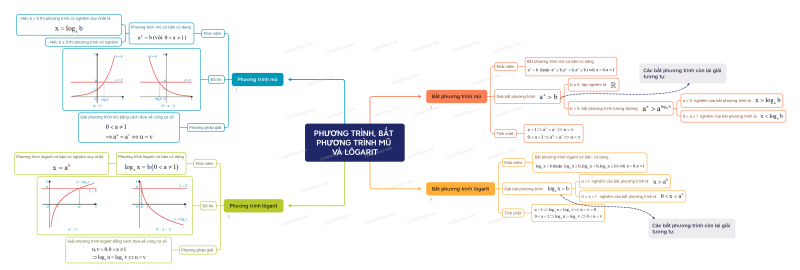
Xem thêm lời giải SBT Toán 11 sách Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 5 trang 87

Bài 18: Lũy thừa với số mũ thực

Bài 19: Lôgarit

Bài 20: Hàm số mũ và hàm số lôgarit

Bài tập cuối chương 6 trang 20