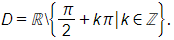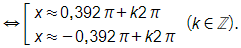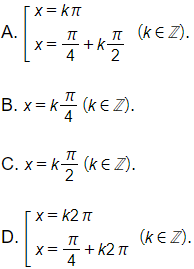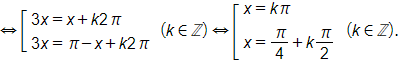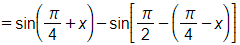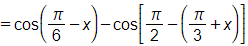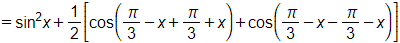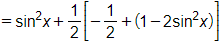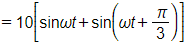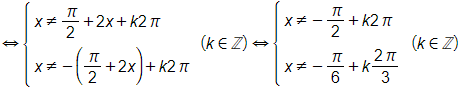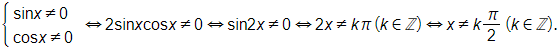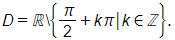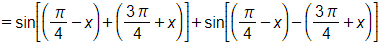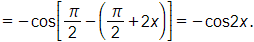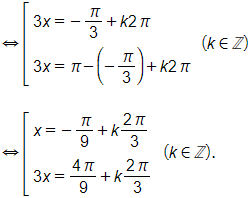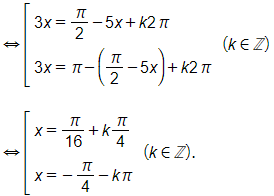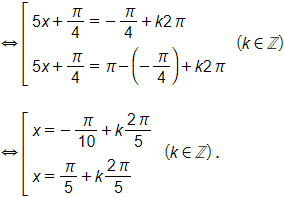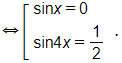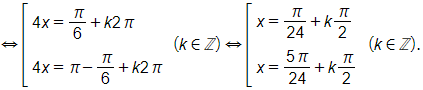Sách bài tập Toán 11 (Kết nối tri thức) Bài tập cuối chương 1 trang 25
Với giải sách bài tập Toán 11 Bài tập cuối chương 1 trang 25 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 11.
Giải SBT Toán 11 Bài tập cuối chương 1 trang 25
A. TRẮC NGHIỆM
Bài 1.31 trang 25 SBT Toán 11 Tập 1: Đổi số đo góc α = 105° sang rađian ta được
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: C
Ta có α = 105° = rad.
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: A
Vì có vô số góc lượng giác tia đầu Ou, tia cuối Ov nên ta loại trừ đáp án B, C, D (do chưa thể xác định được khoảng cụ thể của góc α.
Mà là góc tù nên .
Vậy tồn tại số nguyên k để .
Bài 1.33 trang 25 SBT Toán 11 Tập 1: Giá trị bằng
A. .
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: C
Ta có .
Bài 1.34 trang 25 SBT Toán 11 Tập 1: Cho . Mệnh đề nào sau đây đúng?
B. sin α > 0; cos α > 0.
C. sin α < 0; cos α < 0.
D. sin α > 0; cos α < 0.
Lời giải:
Đáp án đúng là: D
Vì nên α thuộc góc phần tư thứ II, do đó sin α > 0, cos α < 0.
Bài 1.35 trang 25 SBT Toán 11 Tập 1: Trong các đẳng thức sau, đẳng thức nào sai?
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: D
Theo mối quan hệ giữa giá trị lượng giác của hai góc phụ nhau, ta có:
; nên đáp án A và C đúng.
Ta có 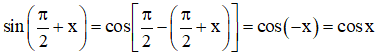
Lại có 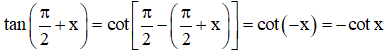
Bài 1.36 trang 26 SBT Toán 11 Tập 1: Trong các đẳng thức sau, đẳng thức nào đúng?
B. sin(180° – a) = – sin a.
C. sin(180° – a) = sin a.
D. sin(180° – a) = cos a.
Lời giải:
Đáp án đúng là: C
Theo mối quan hệ giữa giá trị lượng giác của hai góc bù nhau, ta có: sin(180° – a) = sin a.
Bài 1.37 trang 26 SBT Toán 11 Tập 1: Biết sin x = . Giá trị của cos2 x bằng
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: D
Ta có sin2 x + cos2 x = 1, suy ra cos2 x = 1 – sin2 x = .
Bài 1.38 trang 26 SBT Toán 11 Tập 1: Biết cot x = . Giá trị của biểu thức bằng
A. .
B. .
C. 13.
D. .
Lời giải:
Đáp án đúng là: C
Vì cot x = nên sin x ≠ 0, ta chia cả tử và mẫu của biểu thức cho sin x, ta được:
.
Bài 1.39 trang 26 SBT Toán 11 Tập 1: Trong các đẳng thức sau, đẳng thức nào sai?
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: B
Công thức biến đổi tổng thành tích:
.
.
.
.
Vậy đáp án B sai.
Bài 1.40 trang 26 SBT Toán 11 Tập 1: Trong các đẳng thức sau, đẳng thức nào sai?
B. cos 2a = cos2 a – sin2 a.
C. cos 2a = 1 – 2sin2 a.
D. tan 2a = .
Lời giải:
Đáp án đúng là: D
Công thức nhân đôi:
sin 2a = 2sin a cos a.
cos 2a = cos2 a – sin2 a = 1 – 2sin2 a.
tan 2a = .
Vậy đáp án D sai.
Bài 1.41 trang 26 SBT Toán 11 Tập 1: Tập xác định của hàm số là
Lời giải:
Đáp án đúng là: D
Biểu thức xác định khi 1 – cos x ≥ 0.
Vì – 1 ≤ cos x ≤ 1 nên 1 – cos x ≥ 0 với mọi x ∈ ℝ.
Vậy tập xác định của hàm số là D = ℝ.
Bài 1.42 trang 26 SBT Toán 11 Tập 1: Khẳng định nào sau đây đúng?
A. Hàm số y = cos x nghịch biến trên khoảng (– π; 0) và đồng biến khoảng (0; π).
B. Hàm số y = cos x đồng biến trên các khoảng (– π; 0) và (0; π).
C. Hàm số y = cos x nghịch biến trên các khoảng (– π; 0) và (0; π).
D. Hàm số y = cos x đồng biến trên khoảng (– π; 0) và nghịch biến trên khoảng (0; π).
Lời giải:
Đáp án đúng là: D
Hàm số y = cos x đồng biến trên mỗi khoảng (– π + k2π; k2π) và nghịch biến trên mỗi khoảng (k2π; π + k2π), k ∈ ℤ.
Do đó, hàm số y = cos x đồng biến trên khoảng (– π; 0) và nghịch biến trên khoảng (0; π).
Bài 1.43 trang 27 SBT Toán 11 Tập 1: Khẳng định nào sau đây sai?
A. Tập xác định của hàm số y = tan x là
B. Hàm số y = tan x đồng biến trên các khoảng với mọi k ∈ ℤ.
C. Tập giá trị của hàm số y = tan x là .
D. Hàm số y = tan x là hàm số tuần hoàn với chu kì π.
Lời giải:
Đáp án đúng là: C
Theo lí thuyết, ta có các đáp án A, B, D đúng.
Lại có tập giá trị của hàm số y = tan x là ℝ nên đáp án C sai.
Bài 1.44 trang 27 SBT Toán 11 Tập 1: Hàm số nào dưới đây có đồ thị nhận trục tung làm trục đối xứng?
B. y = sin3 x .
C. y = sin x.
D. y = tan x.
Lời giải:
Đáp án đúng là: A
Hàm số y = cos x là hàm số chẵn nên đồ thị của nó nhận trục tung làm trục đối xứng.
Bài 1.45 trang 27 SBT Toán 11 Tập 1: Mệnh đề nào sau đây sai?
A. Hàm số y = sin x tuần hoàn với chu kì 2π.
B. Hàm số y = cos x tuần hoàn với chu kì 2π.
C. Hàm số y = tan x tuần hoàn với chu kì 2π.
D. Hàm số y = cot x tuần hoàn với chu kì π.
Lời giải:
Đáp án đúng là: C
Hàm số y = tan x tuần hoàn với chu kì π nên đáp án C sai.
Bài 1.46 trang 27 SBT Toán 11 Tập 1: Mệnh đề nào sau đây sai?
A. Hàm số y = sin x cos 2x là hàm số tuần hoàn.
B. Hàm số y = sin x cos 2x là hàm số lẻ.
C. Hàm số y = x sin x là hàm số tuần hoàn.
D. Hàm số y = x sin x là hàm số chẵn.
Lời giải:
Đáp án đúng là: C
Xét từng đáp án:
+) Hàm số y = sin x cos 2x có tập xác định D = ℝ.
- Ta có ∀ x ∈ D thì x + 2π ∈ D và x – 2π ∈ D, hơn nữa
f(x + 2π) = sin(x + 2π) cos(2x + 2π) = sin x cos 2x = f(x).
Vậy hàm số y = sin x cos 2x là hàm số tuần hoàn nên đáp án A đúng.
- Ta có ∀ x ∈ D thì – x ∈ D và f(– x) = sin(– x) . cos(– 2x) = – sin x . cos 2x = – f(x).
Do đó hàm số y = sin x cos 2x là hàm số lẻ nên đáp án B đúng.
+) Hàm số y = x sin x có tập xác định D = ℝ.
Ta có ∀ x ∈ D thì – x ∈ D và f(– x) = (– x) . sin(– x) = x sin x = f(x).
Do đó hàm số y = x sin x là hàm số chẵn nên đáp án D đúng.
Vậy đáp án C sai.
Bài 1.47 trang 27 SBT Toán 11 Tập 1: Mệnh đề nào dưới đây đúng?
A. cos x = – 1 ⇔ x = π + k2π (k ∈ ℤ).
B. sin x = 0 ⇔ x = k2π (k ∈ ℤ).
C. tan x = 0 ⇔ x = k2π (k ∈ ℤ).
D. cos x = 0 ⇔ x = + k2π (k ∈ ℤ).
Lời giải:
Đáp án đúng là: A
Xét từng đáp án:
+) cos x = – 1 ⇔ x = π + k2π (k ∈ ℤ) nên đáp án A đúng.
+) sin x = 0 ⇔ x = kπ (k ∈ ℤ) nên đáp án B sai, từ đó suy ra đáp án C sai.
+) cos x = 0 ⇔ x = + kπ (k ∈ ℤ) nên đáp án D sai.
Bài 1.48 trang 27 SBT Toán 11 Tập 1: Số nghiệm của phương trình trên đoạn ![Số nghiệm của phương trình 2cosx = căn bậc hai 3 trên đoạn [0;5π/2] là](https://vietjack.com/sbt-toan-11-kn/images/bai-1-48-trang-27-sbt-toan-lop-11-tap-1.PNG)
A. 1.
B. 4.
C. 3.
D. 2.
Lời giải:
Đáp án đúng là: C
Ta có .
Vì ![Số nghiệm của phương trình 2cosx = căn bậc hai 3 trên đoạn [0;5π/2] là](https://vietjack.com/sbt-toan-11-kn/images/bai-1-48-trang-27-sbt-toan-lop-11-tap-1-1.PNG)
+ Với thì , mà k ∈ ℤ, từ đó suy ra k ∈ {0; 1}.
+ Với thì , mà k ∈ ℤ, từ đó suy ra k = 1.
Vậy phương trình có 3 nghiệm trên đoạn ![Số nghiệm của phương trình 2cosx = căn bậc hai 3 trên đoạn [0;5π/2] là](https://vietjack.com/sbt-toan-11-kn/images/bai-1-48-trang-27-sbt-toan-lop-11-tap-1.PNG)
C. S = 4π.
D. S = 3π.
Lời giải:
Đáp án đúng là: A
Ta có 3cos x – 1 = 0
Mà x ∈ (0; 2π) nên x ≈ 0,392π hoặc x ≈ – 0,392π + 2π.
Vậy tổng các nghiệm cần tìm là S = 0,392π + (– 0,392π + 2π) = 2π.
Lời giải:
Đáp án đúng là: A
Giá trị của hai hàm số y = sin3x và y = sin x bằng nhau khi và chỉ khi sin 3x = sin x
B. TỰ LUẬN
a) ; b) ; c) – 1 380°.
Lời giải:
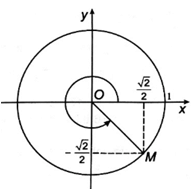
a) Ta có . Góc được biểu diễn bởi điểm trên đường tròn lượng giác (hình dưới).
Vậy và .
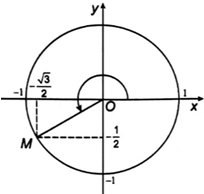
b) Ta có . Góс được biểu diễn bởi điểm > trên đường tròn lượng giác (hình dưới).
Vậy ; và .
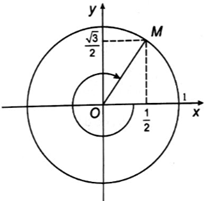
c) Ta có – 1 380° = − 4 . 360° + 60°. Góc –1 380° được biểu diễn bởi điểm trên đường tròn lượng giác (hình dưới).
Vậy sin(– 1 380°) = ; cos(– 1 380°) = ; tan(– 1 380°) = và cot(– 1 380°) = .
Lời giải:
+) Trong 15 phút thì mũi kim phút vạch nên một cung tròn có độ dài bằng độ dài đường tròn, do đó độ dài của cung này bằng
.
+) Trong 15 phút thì mũi kim giờ vạch nên một cung tròn có độ dài bằng đường tròn, do đó độ dài của cung này bằng
.
Lời giải:
Góc ở tâm chắn cung kinh tuyến nối huyện Quản Bạ tỉnh Hà Giang và huyện Cái Nước tỉnh Cà Mau có số đo bằng 23° – 9° = 14°.
Vậy độ dài cung kinh tuyến đó bằng .
Ta có cos 2α = 2 cos2 α – 1 = .
Ta có sin2 α = 1 – cos2 a = = .
Lại do sin α > 0 nên sin α = .
Suy ra sin 2α = 2 sin α cos α = .
Ta có cos 2β = 1 – 2 sin2 β = = .
Ta có cos2 β = 1 – sin2 β = = .
Lại do nên cos β < 0, do đó .
Suy ra sin 2β = 2 sin β cos β = .
Ta có
cos(α + β) = cos α cos β – sin α sin β = .
sin(α – β) = sin α cos β – cos α sin β = .
Bài 1.55 trang 28 SBT Toán 11 Tập 1: Rút gọn các biểu thức sau
b) ;
c) ;
d) .
Lời giải:
a)
.
b)
.
c)
.
d)
.
Bài 1.56 trang 28 SBT Toán 11 Tập 1: Chứng minh các biểu thức sau không phụ thuộc vào x:
b) ;
c) ;
d) .
Lời giải:
a) Cách 1:
.
Vậy biểu thức A không phụ thuộc vào biến x.
Cách 2:
.
Vậy biểu thức A không phụ thuộc vào biến x.
b)
.
Vậy biểu thức B không phụ thuộc vào biến x.
c)
.
Vậy biểu thức C không phụ thuộc vào biến x.
d)
.
Vậy biểu thức D không phụ thuộc vào biến x.
Bài 1.57 trang 29 SBT Toán 11 Tập 1: Hai sóng âm có phương trình lần lượt là
f1(t) = C sin ωt và f2(t) = C sin(ωt + α).
Hai sóng này giao thoa với nhau tạo ra một âm kết hợp có phương trình
f(t) = f1(t) + f2(t) = C sin ωt + C sin(ωt + α).
a) Sử dụng công thức cộng chỉ ra rằng hàm f(t) có thể viết được dưới dạng f(t) = A sin ωt + B cos ωt, ở đó A, B là hai hằng số phụ thuộc vào α.
b) Khi C = 10 và , hãy tìm biên độ và pha ban đầu của sóng âm kết hợp, tức là tìm hai hằng số k và φ sao cho f(t) = k sin(ωt + φ).
Lời giải:
a) Ta có f(t) = f1(t) + f2(t)
= C sin ωt + C sin(ωt + α)
= C sin ωt + C(sin ωt cos α + cos ωt sin α)
= C sin ωt + C sin ωt cos α + C cos ωt sin α
= C(1 + cos α) sin ωt + C sin α cos ωt.
Vậy f(t) = C(1 + cos α) sin ωt + C sin α cos ωt với A = C(1 + cos α) và B = C sin α.
b) Khi C = 10 và ta có
.
Vậy biên độ và pha ban đầu của sóng âm kết hợp lần lượt là và .
Bài 1.58 trang 29 SBT Toán 11 Tập 1: Tìm tập xác định của các hàm số sau:
b) ;
c) ;
d) y = tan x + cot x.
Lời giải:
a) Biểu thức có nghĩa khi x – 1 ≠ 0 hay x ≠ 1.
Vậy tập xác định của hàm số là 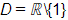
b) Biểu thức có nghĩa khi cos x – cos 3x ≠ 0 hay cos x ≠ cos 3x
⇔ 3x ≠ ± x + k2π (k ∈ ℤ) ⇔ x ≠ k(k ∈ ℤ). .
Vậy tập xác định của hàm số là 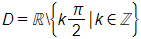
c) Biểu thức có nghĩa khi cos x + sin 2x ≠ 0 ⇔ cos x ≠ – sin 2x
⇔ cos x ≠ sin (– 2x)
Vậy tập xác định của hàm số là 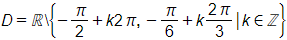
d) Biểu thức tan x + cot x có nghĩa khi
Vậy tập xác định của hàm số là 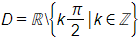
Bài 1.59 trang 29 SBT Toán 11 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của p
c) y = sin4 x + cos4 x;
d) y = cos 2x + 2cos x – 1.
Lời giải:
a) Ta có y = sin x – cos x = .
Vì nên , với mọi .
Vậy giá trị lớn nhất của hàm số là , đạt được khi
>.
Giá trị nhỏ nhất của hàm số là , đạt được khi
.
b) Ta có y = sin x + sin
.
Ta có .
Vậy giá trị lớn nhất của hàm số là 1, đạt được khi và giá trị nhỏ nhất của hàm số là – 1, đạt được khi .
c) Ta có y = sin4 x + cos4 x = (sin2 x + cos2 x)2 – 2sin2 x cos2 x
= 1 – 2 (sin x cos x)2 = =
= = = .
Vì – 1 ≤ cos 4x ≤ 1 nên , do đó
hay .
Vậy giá trị lớn nhất của hàm số là 1, đạt được khi cos 4x = 1 ⇔ 4x = k2π (k ∈ ℤ)
.
Giá trị nhỏ nhất của hàm số là , đạt được khi cos 4x = – 1 ⇔ 4x = π + k2π (k ∈ ℤ)
.
d) Ta có y = cos 2x + 2cos x − 1
= (2cos2 x – 1) + 2cos x – 1
= 2cos2 x + 2cos x – 2
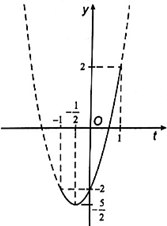
= 2t2 + 2t – 2 với t = cos x ∈ [– 1; 1].
Xét hàm số y = 2t2 + 2t – 2 trên đoạn [– 1; 1]. Hàm số này có đồ thị như trong hình vẽ dưới đây.
Từ đồ thị ở hình trên ta suy ra được giá trị lớn nhất của hàm số đã cho là 2, đạt được khi cos x = 1 ⇔ x = k2π (k ∈ ℤ) và giá trị nhỏ nhất của hàm số là , đạt được khi .
Bài 1.60 trang 29 SBT Toán 11 Tập 1: Xét tính chẵn lẻ của các hàm số sau:
c) y = sin 2x + cos x;
d) .
Lời giải:
a) Tập xác định của hàm số y = sin3 x – cot x là D = ℝ \ {kπ | k ∈ ℤ}.
Nếu kí hiệu f(x) = sin3 x + cot x thì với mọi x ∈ D ta có: – x ∈ D và
f(– x) = sin3 (–x) – cot(– x) = – sin3 x + cot x = – (sin3 x – cot x) = – f(x).
Vậy hàm số đã cho là hàm số lẻ.
b) Tập xác định của hàm số là
Nếu kí hiệu thì với mọi x ∈ D ta có: – x ∈ D và
Vậy hàm số đã cho là hàm số chẵn.
c) Tập xác định của hàm số y = sin 2x + cos x là D = ℝ.
Nếu kí hiệu f(x) = sin 2x + cos x thì với mọi x ∈ D ta có: – x ∈ D và
f(– x) = sin [2(– x)] + cos (– x) = – sin 2x + cos x ≠ ± f(x).
Vậy hàm số đã cho là hàm số không chẵn cũng không lẻ.
d) Tập xác định của hàm số là D = ℝ.
Ta có
Nếu kí hiệu thì với mọi x ∈ D ta có: – x ∈ D và f(– x) = – cos (– 2x) = – cos 2x = f(x).
Vậy hàm số đã cho là hàm số chẵn.
Bài 1.61 trang 29 SBT Toán 11 Tập 1: Xét tính tuần hoàn của các hàm số sau:
Lời giải:
a) Hàm số y = sin tuần hoàn với chu kì T1 = , hàm số y = cos 3x tuần hoàn với chu kì T2 = . Ta có .
Ta chỉ ra rằng hàm số f(x) = = sin + cos 3x tuần hoàn như sau:
.
Vậy hàm số đã cho là hàm số tuần hoàn với chu kì T = 4π.
b) Hàm số y = cos 5x tuần hoàn với chu kì T1 = , hàm số y = tan hoàn với chu kì .
Ta có .
Ta có thể chỉ ra hàm số f(x) = cos5x + tan tuần hoàn như sau
.
Vậy hàm số đã cho là hàm số tuần hoàn với chu kì T = 6π.
Bài 1.62 trang 29 SBT Toán 11 Tập 1: Giải các phương trình sau:
c) sin 3x – cos 5x = 0;
d) tan 3x tan x = 1.
Lời giải:
a) Ta có
b) Ta có
⇔ + 10° = – 30° + k180° (k ∈ ℤ)
⇔ x = – 120° + k540° (k ∈ ℤ).
c) Ta có sin 3x – cos 5x = 0
⇔ sin 3x = cos 5x
d) Điều kiện cos 3x ≠ 0 và cos x ≠ 0 ⇔ cos3x ≠ 0 .
Ta có tan 3x tan x = 1
⇔ tan 3x = cot x
.
Ta thấy thoả mãn điều kiện.
Vậy nghiệm của phương trình là .
Bài 1.63 trang 30 SBT Toán 11 Tập 1: Giải các phương trình sau:
Lời giải:
a) Ta có sin 5x + cos 5x = – 1
b) Ta có cos 3x – cos 5x = sin x
+ Với sin x = 0 ta được x = kπ (k ∈ ℤ).
+ Với
c) Ta có 2 cos2 x + cos 2x = 2
⇔ (2 cos2 x – 1) + cos 2x = 1
⇔ cos 2x + cos 2x = 1
⇔ 2cos 2x = 1
⇔ cos 2x =
⇔ cos 2x =
⇔ 2x =
.
d) Ta có sin4 x + cos4 x = sin2 2x
(do sin2 2x + cos2 2x = 1)
.
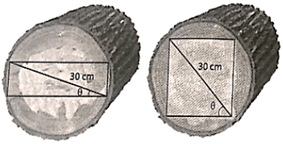
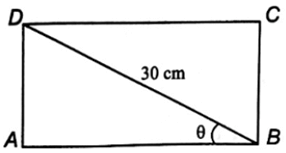
a) Chứng minh rằng diện tích mặt cắt của thanh xà gồ được tính bởi công thức
ở đó góc θ được chỉ ra trong hình vẽ dưới đây.
b) Tìm góc θ để diện tích mặt cắt của thanh xà gồ là lớn nhất.
Lời giải:
a) Mặt cắt của thanh xà gồ (hình dưới) là hình chữ nhật có hai kích thước là
AB = 30cos θ và BC = 30sin θ.
Vậy diện tích mặt cắt là S = AB ∙ BC = 30cos θ ∙ 30sin θ = 450sin 2θ.
b) Vì – 1 ≤ sin 2θ ≤ 1 nên ta có S = 450sin 2θ ≤ 450.
Vậy diện tích mặt cắt của thanh xà gồ lớn nhất khi sin 2θ = 1 hay góc θ = 45°.
ở đó P(t) là huyết áp tính theo đơn vị mmHg (milimét thuỷ ngân) và thời gian t tính theo giây.
a) Trong khoảng từ 0 đến 1 giây, hãy xác định số lần huyết áp là 100 mmHg.
b) Trong khoảng từ 0 đến 1 giây, hãy xác định số lần huyết áp là 120 mmHg
Lời giải:
a) Huyết áp là 100 mmHg khi
.
Xét 0 < t < 1 . Suy ra k ∈ {1; 2} vì k ∈ ℤ.
Vậy trong khoảng từ 0 đến 1 giây, có 2 lần huyết áp là 100 mmHg.
b) Huyết áp là 120 mmHg khi
.
Xét 0 < t < 1 . Suy ra k = 0 vì k ∈ ℤ.
Vậy trong khoảng từ 0 đến 1 giây, có 1 lần huyết áp là 120 mmHg.
a) Huyết áp là 100 mmHg khi
.
Xét 0 < t < 1 . Suy ra k ∈ {1; 2} vì k ∈ ℤ.
Vậy trong khoảng từ 0 đến 1 giây, có 2 lần huyết áp là 100 mmHg.
b) Huyết áp là 120 mmHg khi
.
Xét 0 < t < 1 . Suy ra k = 0 vì k ∈ ℤ.
Vậy trong khoảng từ 0 đến 1 giây, có 1 lần huyết áp là 120 mmHg.
Xem thêm lời giải SBT Toán 11 sách Kết nối tri thức hay, chi tiết khác:
Xem thêm các chương trình khác:
- Soạn văn lớp 11 Kết nối tri thức - hay nhất
- Văn mẫu lớp 11 - Kết nối tri thức
- Tóm tắt tác phẩm Ngữ văn 11 – Kết nối tri thức
- Tác giả tác phẩm Ngữ văn 11 - Kết nối tri thức
- Giải SBT Ngữ văn 11 – Kết nối tri thức
- Bố cục tác phẩm Ngữ văn 11 – Kết nối tri thức
- Giải Chuyên đề học tập Ngữ văn 11 – Kết nối tri thức
- Nội dung chính tác phẩm Ngữ văn lớp 11 – Kết nối tri thức
- Soạn văn 11 Kết nối tri thức (ngắn nhất)
- Bài tập Tiếng Anh 11 Global success theo Unit có đáp án
- Giải sgk Tiếng Anh 11 – Global success
- Giải sbt Tiếng Anh 11 - Global Success
- Trọn bộ Từ vựng Tiếng Anh 11 Global success đầy đủ nhất
- Ngữ pháp Tiếng Anh 11 Global success
- Giải sgk Vật lí 11 – Kết nối tri thức
- Lý thuyết Vật lí 11 – Kết nối tri thức
- Giải sbt Vật lí 11 – Kết nối tri thức
- Giải Chuyên đề học tập Vật lí 11 – Kết nối tri thức
- Chuyên đề dạy thêm Vật lí 11 cả 3 sách (2024 có đáp án)
- Giải sgk Hóa học 11 – Kết nối tri thức
- Giải Chuyên đề học tập Hóa học 11 – Kết nối tri thức
- Lý thuyết Hóa 11 - Kết nối tri thức
- Giải sbt Hóa học 11 – Kết nối tri thức
- Chuyên đề dạy thêm Hóa 11 cả 3 sách (2024 có đáp án)
- Giải sgk Sinh học 11 – Kết nối tri thức
- Lý thuyết Sinh học 11 – Kết nối tri thức
- Giải Chuyên đề học tập Sinh học 11 – Kết nối tri thức
- Giải sbt Sinh học 11 – Kết nối tri thức
- Giải sgk Giáo dục Kinh tế và Pháp luật 11 – Kết nối tri thức
- Giải Chuyên đề học tập Kinh tế pháp luật 11 – Kết nối tri thức
- Lý thuyết Kinh tế pháp luật 11 – Kết nối tri thức
- Giải sbt Kinh tế pháp luật 11 – Kết nối tri thức
- Giải sgk Lịch sử 11 – Kết nối tri thức
- Giải Chuyên đề học tập Lịch sử 11 – Kết nối tri thức
- Lý thuyết Lịch sử 11 - Kết nối tri thức
- Giải sbt Lịch sử 11 – Kết nối tri thức
- Giải sgk Địa lí 11 – Kết nối tri thức
- Giải Chuyên đề học tập Địa lí 11 – Kết nối tri thức
- Lý thuyết Địa lí 11 - Kết nối tri thức
- Giải sbt Địa lí 11 – Kết nối tri thức
- Giải sgk Công nghệ 11 – Kết nối tri thức
- Lý thuyết Công nghệ 11 - Kết nối tri thức
- Giải sbt Công nghệ 11 – Kết nối tri thức
- Giải sgk Tin học 11 – Kết nối tri thức
- Giải Chuyên đề học tập Tin học 11 – Kết nối tri thức
- Lý thuyết Tin học 11 - Kết nối tri thức
- Giải sbt Tin học 11 – Kết nối tri thức
- Giải sgk Giáo dục quốc phòng an ninh 11 – Kết nối tri thức
- Lý thuyết Giáo dục quốc phòng 11 – Kết nối tri thức
- Giải sbt Giáo dục quốc phòng 11 – Kết nối tri thức
- Giải sgk Hoạt động trải nghiệm 11 – Kết nối tri thức