Số nghiệm của phương trình 2cos x = căn 3 trên đoạn [0; 5pi/2] là
Lời giải Bài 1.48 trang 27 SBT Toán 11 Tập 1 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11.
Giải SBT Toán 11 Bài tập cuối chương 1 trang 25
Bài 1.48 trang 27 SBT Toán 11 Tập 1: Số nghiệm của phương trình 2cosx=√3 trên đoạn ![Số nghiệm của phương trình 2cosx = căn bậc hai 3 trên đoạn [0;5π/2] là](https://vietjack.com/sbt-toan-11-kn/images/bai-1-48-trang-27-sbt-toan-lop-11-tap-1.PNG)
A. 1.
B. 4.
C. 3.
D. 2.
Đáp án đúng là: C
Lời giải:
Ta có 2cosx=√3⇔cosx=√32⇔cosx=cosπ6⇔x=±π6+k2π (k∈ℤ).
Vì ![Số nghiệm của phương trình 2cosx = căn bậc hai 3 trên đoạn [0;5π/2] là](https://vietjack.com/sbt-toan-11-kn/images/bai-1-48-trang-27-sbt-toan-lop-11-tap-1-1.PNG)
+ Với x=π6+k2π (k∈ℤ) thì 0≤π6+k2π≤5π2⇔−112≤k≤76 , mà k ∈ ℤ, từ đó suy ra k ∈ {0; 1}.
+ Với x=π6+k2π (k∈ℤ) thì 0≤−π6+k2π≤5π2⇔112≤k≤43, mà k ∈ ℤ, từ đó suy ra k = 1.
Vậy phương trình 2cosx=√3 có 3 nghiệm trên đoạn ![Số nghiệm của phương trình 2cosx = căn bậc hai 3 trên đoạn [0;5π/2] là](https://vietjack.com/sbt-toan-11-kn/images/bai-1-48-trang-27-sbt-toan-lop-11-tap-1.PNG)
*Phương pháp giải:
- Nếu m biểu diễn được dưới dạng cos của những góc đặc biệt thì:
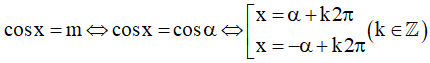
-Xét nghiệm trên đoạn đề bài yêu cầu
-Kết luận
*Lý thuyết:
* Công thức nghiệm cơ bản
a) Phương trình sin x = m
Trường hợp 1: |m| > 1. Phương trình vô nghiệm.
Trường hợp 2: |m| ≤ 1. Phương trình có nghiệm.
- Nếu m biểu diễn được dưới dạng sin của những góc đặc biệt thì:
sinx = m ⇔ sinx = sinα ⇔ 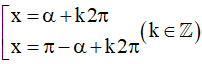
- Nếu m không biểu diễn được dưới dạng sin của những góc đặc biệt thì:
sinx = m ⇔ 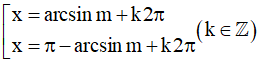
- Các trường hợp đặc biệt:
sinx = 0 ⇔ x = kπ (k ∈ Z)
sinx = 1 ⇔ x = 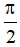 + k2π (k ∈ Z)
+ k2π (k ∈ Z)
sinx = -1 ⇔ x = -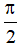 + k2π (k ∈ Z)
+ k2π (k ∈ Z)
b) Phương trình cos x = m
Trường hợp 1: |m| > 1. Phương trình vô nghiệm.
Trường hợp 2: |m| ≤ 1 . Phương trình có nghiệm.
- Nếu m biểu diễn được dưới dạng cos của những góc đặc biệt thì:
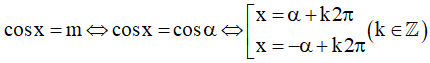
- Nếu m không biểu diễn được dưới dạng cos của những góc đặc biệt thì:
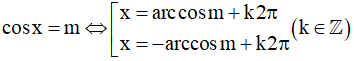
- Các trường hợp đặc biệt:
cosx = 0 ⇔ x = 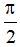 + kπ (k ∈ Z)
+ kπ (k ∈ Z)
cosx = 1 ⇔ x = k2π (k ∈ Z)
cosx = -1 ⇔ x = π + k2π (k ∈ Z)
c) Phương trình: tan x = m. Điều kiện: x ≠ 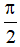 + kπ (k ∈ Z)
+ kπ (k ∈ Z)
- Nếu m biểu diễn được dưới dạng tan của những góc đặc biệt thì:
tan x = m ⇔ tan x = tan α ⇔ x = α + kπ (k ∈ Z)
- Nếu m không biểu diễn được dưới dạng tan của những góc đặc biệt thì:
tan x = m ⇔ x = αrctan m + kπ (k ∈ Z)
d) Phương trình: cot x = m. Điều kiện: x ≠ kπ (k ∈ Z)
- Nếu m biểu diễn được dưới dạng cot của những góc đặc biệt thì:
cot x = m ⇔ cot x = cot α ⇔ x = α + kπ (k ∈ Z)
- Nếu m không biểu diễn được dưới dạng cot của những góc đặc biệt thì:
cot x = m ⇔ x = αrccot m + kπ (k ∈ Z)
* Mở rộng công thức nghiệm, với u(x) và v(x) là hai biểu thức của x.
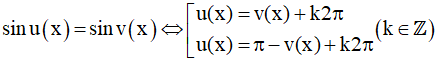
cos u(x) = cos v(x) ⇔ u(x) = 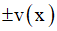 + k2π (k ∈ Z)
+ k2π (k ∈ Z)
tan u(x) = tan v(x) ⇔ u(x) = v(x) + kπ (k ∈ Z)
cot u(x) = cot v(x) ⇔ u(x) = v(x) + kπ (k ∈ Z)
Xem thêm
TOP 40 câu Trắc nghiệm Phương trình lượng giác cơ bản (có đáp án 2023) – Toán 11
Lý thuyết Phương trình lượng giác cơ bản (mới + Bài Tập) – Toán 11
Xem thêm lời giải SBT Toán 11 sách Kết nối tri thức hay, chi tiết khác:
Bài 1.31 trang 25 SBT Toán 11 Tập 1: Đổi số đo góc α = 105° sang rađian ta được ...
Bài 1.32 trang 25 SBT Toán 11 Tập 1: Cho góc lượng giác (Ou, Ov) có số đo α mà...
Bài 1.33 trang 25 SBT Toán 11 Tập 1: Giá trị cot89π6 bằng...
Bài 1.34 trang 25 SBT Toán 11 Tập 1: Cho π2<α<π. Mệnh đề nào sau đây đúng?....
Bài 1.35 trang 25 SBT Toán 11 Tập 1: Trong các đẳng thức sau, đẳng thức nào sai?...
Bài 1.36 trang 26 SBT Toán 11 Tập 1: Trong các đẳng thức sau, đẳng thức nào đúng? A. sin(180° – a) = – cos a....
Bài 1.37 trang 26 SBT Toán 11 Tập 1: Biết sin x = 12 . Giá trị của cos2 x bằng...
Bài 1.38 trang 26 SBT Toán 11 Tập 1: Biết cot x = 12. Giá trị của biểu thức...
Bài 1.39 trang 26 SBT Toán 11 Tập 1: Trong các đẳng thức sau, đẳng thức nào sai? A. cosu+cosv=2cosu+v2cosu−v2...
Bài 1.40 trang 26 SBT Toán 11 Tập 1: Trong các đẳng thức sau, đẳng thức nào sai? A. sin 2a = 2sin a cos a...
Bài 1.41 trang 26 SBT Toán 11 Tập 1: Tập xác định của hàm số...
Bài 1.42 trang 26 SBT Toán 11 Tập 1: Khẳng định nào sau đây đúng?..
Bài 1.43 trang 27 SBT Toán 11 Tập 1: Khẳng định nào sau đây sai?...
Bài 1.45 trang 27 SBT Toán 11 Tập 1: Mệnh đề nào sau đây sai?...
Bài 1.46 trang 27 SBT Toán 11 Tập 1: Mệnh đề nào sau đây sai? A. Hàm số y = sin x cos 2x là hàm số tuần hoàn....
Bài 1.47 trang 27 SBT Toán 11 Tập 1: Mệnh đề nào dưới đây đúng?...
Bài 1.48 trang 27 SBT Toán 11 Tập 1: Số nghiệm của phương trình 2cosx=√3 trên đoạn...
Bài 1.54 trang 28 SBT Toán 11 Tập 1: Cho cos α = 34, sin α > 0;...
Bài 1.55 trang 28 SBT Toán 11 Tập 1: Rút gọn các biểu thức sau a) sin(45°+α)−cos(45°+α)sin(45°+α)+cos(45°+α);
Bài 1.56 trang 28 SBT Toán 11 Tập 1: Chứng minh các biểu thức sau không phụ thuộc vào x: a) A=sin(π4+x)−cos(π4−x);...
Bài 1.57 trang 29 SBT Toán 11 Tập 1: Hai sóng âm có phương trình lần lượt là...
Bài 1.58 trang 29 SBT Toán 11 Tập 1: Tìm tập xác định của các hàm số sau:a) y=cos2xx−1;...
Bài 1.59 trang 29 SBT Toán 11 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của p a) y = sin x – cos x;...
Bài 1.60 trang 29 SBT Toán 11 Tập 1: Xét tính chẵn lẻ của các hàm số sau: a) y = sin3 x – cot x;...
Bài 1.61 trang 29 SBT Toán 11 Tập 1: Xét tính tuần hoàn của các hàm số sau: a) y = sinx2 + cos 3x;
Bài 1.62 trang 29 SBT Toán 11 Tập 1: Giải các phương trình sau: a) sin3x=−√32;...
Bài 1.63 trang 30 SBT Toán 11 Tập 1: Giải các phương trình sau: a) sin 5x + cos 5x = – 1;...
Xem thêm lời giải SBT Toán 11 sách Kết nối tri thức hay, chi tiết khác:
Xem thêm các chương trình khác:
- Soạn văn lớp 11 Kết nối tri thức - hay nhất
- Văn mẫu lớp 11 - Kết nối tri thức
- Tóm tắt tác phẩm Ngữ văn 11 – Kết nối tri thức
- Tác giả tác phẩm Ngữ văn 11 - Kết nối tri thức
- Giải SBT Ngữ văn 11 – Kết nối tri thức
- Bố cục tác phẩm Ngữ văn 11 – Kết nối tri thức
- Giải Chuyên đề học tập Ngữ văn 11 – Kết nối tri thức
- Nội dung chính tác phẩm Ngữ văn lớp 11 – Kết nối tri thức
- Soạn văn 11 Kết nối tri thức (ngắn nhất)
- Bài tập Tiếng Anh 11 Global success theo Unit có đáp án
- Giải sgk Tiếng Anh 11 – Global success
- Giải sbt Tiếng Anh 11 - Global Success
- Trọn bộ Từ vựng Tiếng Anh 11 Global success đầy đủ nhất
- Ngữ pháp Tiếng Anh 11 Global success
- Giải sgk Vật lí 11 – Kết nối tri thức
- Lý thuyết Vật lí 11 – Kết nối tri thức
- Giải sbt Vật lí 11 – Kết nối tri thức
- Giải Chuyên đề học tập Vật lí 11 – Kết nối tri thức
- Chuyên đề dạy thêm Vật lí 11 cả 3 sách (2024 có đáp án)
- Giải sgk Hóa học 11 – Kết nối tri thức
- Giải Chuyên đề học tập Hóa học 11 – Kết nối tri thức
- Lý thuyết Hóa 11 - Kết nối tri thức
- Giải sbt Hóa học 11 – Kết nối tri thức
- Chuyên đề dạy thêm Hóa 11 cả 3 sách (2024 có đáp án)
- Giải sgk Sinh học 11 – Kết nối tri thức
- Lý thuyết Sinh học 11 – Kết nối tri thức
- Giải Chuyên đề học tập Sinh học 11 – Kết nối tri thức
- Giải sbt Sinh học 11 – Kết nối tri thức
- Giải sgk Giáo dục Kinh tế và Pháp luật 11 – Kết nối tri thức
- Giải Chuyên đề học tập Kinh tế pháp luật 11 – Kết nối tri thức
- Lý thuyết Kinh tế pháp luật 11 – Kết nối tri thức
- Giải sbt Kinh tế pháp luật 11 – Kết nối tri thức
- Giải sgk Lịch sử 11 – Kết nối tri thức
- Giải Chuyên đề học tập Lịch sử 11 – Kết nối tri thức
- Lý thuyết Lịch sử 11 - Kết nối tri thức
- Giải sbt Lịch sử 11 – Kết nối tri thức
- Giải sgk Địa lí 11 – Kết nối tri thức
- Giải Chuyên đề học tập Địa lí 11 – Kết nối tri thức
- Lý thuyết Địa lí 11 - Kết nối tri thức
- Giải sbt Địa lí 11 – Kết nối tri thức
- Giải sgk Công nghệ 11 – Kết nối tri thức
- Lý thuyết Công nghệ 11 - Kết nối tri thức
- Giải sbt Công nghệ 11 – Kết nối tri thức
- Giải sgk Tin học 11 – Kết nối tri thức
- Giải Chuyên đề học tập Tin học 11 – Kết nối tri thức
- Lý thuyết Tin học 11 - Kết nối tri thức
- Giải sbt Tin học 11 – Kết nối tri thức
- Giải sgk Giáo dục quốc phòng an ninh 11 – Kết nối tri thức
- Lý thuyết Giáo dục quốc phòng 11 – Kết nối tri thức
- Giải sbt Giáo dục quốc phòng 11 – Kết nối tri thức
- Giải sgk Hoạt động trải nghiệm 11 – Kết nối tri thức
