a) Vẽ đồ thị của hai hàm số y = e^x và y = ln x trên cùng một hệ trục tọa độ

Lời giải Bài 6.56 trang 22 SBT Toán 11 Tập 2 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11.

1 943 05/11/2023

Trang trước

Trang sau

Giải SBT Toán 11 Bài tập cuối chương 6 trang 20

Bài 6.56 trang 22 SBT Toán 11 Tập 2:

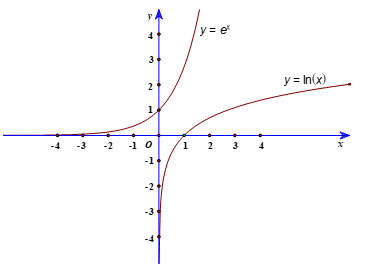
a) Vẽ đồ thị của hai hàm số y = e^x và y = ln x trên cùng một hệ trục tọa độ.

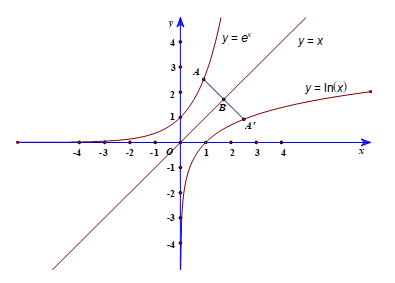
b) Chứng minh rằng hai đồ thị trên đối xứng nhau qua đường thẳng y = x, tức là nếu điểm M nằm trên một đồ thị thì điểm M’ đối xứng với M qua đường thẳng y = x sẽ nằm trên đồ thị còn lại.

Lời giải:

a) Đồ thị của hai hàm số y = e^x và y = ln x trên cùng một hệ trục tọa độ như hình sau:

Vẽ đồ thị của hai hàm số y = e^x và y = ln x trên cùng một hệ trục tọa độ

b) Xét điểm $A (x_{0}; e^{x_{0}})$ nằm trên đồ thị hàm số y = e^x.

Phương trình đường thẳng (d) đi qua điểm $A (x_{0}; e^{x_{0}})$ và vuông góc với đường thẳng y = x có dạng: $y = - x + x_{0} + e^{x_{0}}$ .

Vẽ đồ thị của hai hàm số y = e^x và y = ln x trên cùng một hệ trục tọa độ

Gọi B là giao điểm của đường thẳng (d) và đường thẳng y = x.

Khi đó $B (\frac{x_{0} + e^{x_{0}}}{2}; \frac{x_{0} + e^{x_{0}}}{2})$ .

Gọi A’ là điểm đối xứng với A qua đường thẳng y = x. Khi đó B là trung điểm của AA’.

Do đó: $\{\begin{cases} x_{A^{'}} = 2 x_{B} - x_{A} \\ y_{A^{'}} = 2 y_{B} - y_{A} \end{cases}$ $\Leftrightarrow \{\begin{cases} x_{_{A^{'}}} = 2 \cdot \frac{x_{0} + e^{x_{0}}}{2} - x_{0} \\ y_{_{A^{'}}} = 2 \cdot \frac{x_{0} + e^{x_{0}}}{2} - e^{x_{0}} \end{cases}$ $\Leftrightarrow \{\begin{cases} x_{A^{'}} = e^{x_{0}} \\ y_{A^{'}} = x_{0} \end{cases}$ .Vậy $A^{'} (e^{x_{0}}; x_{0})$

Thay tọa độ điểm $A^{'} (e^{x_{0}}; x_{0})$ vào hàm số y = ln x, ta được $x_{0} = {lne}^{x_{0}}$ (luôn đúng),

Vậy $A^{'} (e^{x_{0}}; x_{0})$ thuộc đồ thị hàm số y = ln x.

Tương tự, nếu B(x₀; ln x₀) nằm trên đồ thị hàm số y = ln x thì ta cũng tìm được điểm B’ đối xứng với B qua đường thẳng y = x và điểm B’ thuộc đồ thị hàm số y = e^x.

Vậy hai đồ thị đã cho đối xứng với nhau qua đường thẳng y = x.

Xem thêm lời giải SBT Toán 11 sách Kết nối tri thức hay, chi tiết khác:

Bài 6.41 trang 20 SBT Toán 11 Tập 2: Cho a là số dương. Rút gọn biểu thức $A = \frac{\sqrt{a} \cdot \sqrt[3]{a^{2}}}{\sqrt[6]{a}}$ , ta được kết quả là...

Bài 6.42 trang 20 SBT Toán 11 Tập 2: Cho a là số dương khác 1. Giá trị của $\log_{a^{3}} a^{2}$ là...

Bài 6.43 trang 20 SBT Toán 11 Tập 2: Giá trị của biểu thức $4^{\log_{\sqrt{2}} 3}$ là...

Bài 6.44 trang 21 SBT Toán 11 Tập 2: Trong các hàm số sau, hàm số nào đồng biến? A. $y = {(\frac{\sqrt{3}}{2})}^{x}$ ....

Bài 6.45 trang 21 SBT Toán 11 Tập 2: Trong các hàm số sau, hàm số nào nghịch biến?...

Bài 6.46 trang 21 SBT Toán 11 Tập 2: Với giá trị nào của x thì đồ thị hàm số $y = {(\frac{2}{3})}^{x}$ nằm phía trên đường thẳng y = 1?...

Bài 6.47 trang 21 SBT Toán 11 Tập 2: Với giá trị nào của x thì đồ thị hàm số y = log_0,5 x nằm phía trên trục hoành?...

Bài 6.48 trang 21 SBT Toán 11 Tập 2: Tập nghiệm của phương trình $8^{2 x - 1} = {(\frac{1}{4})}^{x}$ là...

Bài 6.49 trang 21 SBT Toán 11 Tập 2: Tập nghiệm của phương trình log₂ [x(x – 1)] = 1 là...

Bài 6.50 trang 21 SBT Toán 11 Tập 2: Nghiệm của bất phương trình ${(\frac{1}{2})}^{x} \geq {(\frac{1}{4})}^{2}$ là...