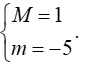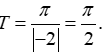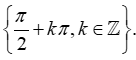Lý thuyết Hàm số lượng giác – Toán 11 Kết nối tri thức

Với lý thuyết Toán lớp 11 Bài 3: Hàm số lượng giác chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sách Kết nối tri thức sẽ giúp học sinh nắm vững kiến thức trọng tâm để học tốt môn Toán 11.

1 3,623 16/09/2024

Trang trước

Trang sau

Lý thuyết Toán 11 Bài 3: Hàm số lượng giác

Bài giảng Toán 11 Bài 3: Hàm số lượng giác

A. Lý thuyết Hàm số lượng giác

1. Định nghĩa hàm số lượng giác

- Quy tắc đặt tương ứng mỗi số thực x với số thực sinx được gọi là hàm số sin, kí hiệu y = sinx. Tập xác định của hàm số sin là $R$ .

- Quy tắc đặt tương ứng mỗi số thực x với số thực cosx được gọi là hàm số cos, kí hiệu y = cosx. Tập xác định của hàm số côsin là $R$ .

- Hàm số cho bằng công thức $y = \frac{\sin α}{\cos α}$ được gọi là hàm số tang, kí hiệu là y = tanx. Tập xác định của hàm số tang là $R ∖ {\frac{π}{2} + k π | k \in Z}$ .

- Hàm số cho bằng công thức $y = \frac{\cos α}{\sin α}$ được gọi là hàm số tang, kí hiệu là y = tanx. Tập xác định của hàm số tang là $R ∖ {k π | k \in Z}$ .

2. Hàm số chẵn, hàm số lẻ, hàm số tuần hoàn

a, Hàm số chẵn, hàm số lẻ

Cho hàm số y = f(x) có tập xác định là D.

+) Hàm số f(x) được gọi là hàm số chẵn nếu $\forall x \in D$ thì $- x \in D$ và $f (- x) = f (x)$ . Đồ thị của một hàm số chẵn nhận trục tung (Oy) làm trục đối xứng.

+) Hàm số f(x) được gọi là hàm số lẻ nếu $\forall x \in D$ thì $- x \in D$ và $f (- x) = - f (x)$ . Đồ thị của một hàm số lẻ nhận gốc tọa độ làm tâm đối xứng.

b, Hàm số tuần hoàn

Hàm số y = f(x) có tập xác định D được gọi là hàm số tuần hoàn nếu tồn tại số T $\neq$ 0 sao cho với mọi $x \in D$ ta có:

+) $x + T \in D$ và $x - T \in D$

+) $f (x + T) = f (x)$

Số T dương nhỏ nhất thỏa mãn cách điều kiện trên (nêu có) được gọi là chu kì của hàm số tuần hoàn đó.

* Nhận xét:

Các hàm số y = sinx, y=cosx tuần hoàn chu kì 2 $π$ .

Các hàm số y = tanx, y=cotx tuần hoàn chu kì $π$ .

3. Đồ thị và tính chất của hàm số y = sinx

- Tập xác định là $R$ .

- Tập giá trị là [-1;1].

- Là hàm số lẻ và tuần hoàn chu kì 2 $π$ .

- Đồng biến trên mỗi khoảng $(- \frac{π}{2} + k 2 π; \frac{π}{2} + k 2 π)$ và nghịch biến trên mỗi khoảng $(\frac{π}{2} + k 2 π; \frac{3 π}{2} + k 2 π)$ .

- Có đồ thị đối xứng qua gốc tọa độ và gọi là một đường hình sin.

4. Đồ thị và tính chất của hàm số y = cosx

Tập xác định là $R$ .

Tập giá trị là [-1;1].

Là hàm số chẵn và tuần hoàn chu kì 2 $π$ .

Đồng biến trên mỗi khoảng $(- π + k 2 π; k 2 π)$ và nghịch biến trên mỗi khoảng $(k 2 π; π + k 2 π)$ .

Có đồ thị là một đường hình sin đối xứng qua trục tung.

5. Đồ thị và tính chất của hàm số y = tanx

Tập xác định là $R ∖ {\frac{π}{2} + k π | k \in Z}$ .

Tập giá trị là $R$ .

Là hàm số lẻ và tuần hoàn chu kì $π$ .

Đồng biến trên mỗi khoảng $(- \frac{π}{2} + k π; \frac{π}{2} + k π)$ , $k \in Z$ .

Có đồ thị đối xứng qua gốc tọa độ.

6. Đồ thị và tính chất của hàm số y = cotx

Tập xác định là $R ∖ {k π | k \in Z}$ .

Tập giá trị là $R$ .

Là hàm số lẻ và tuần hoàn chu kì $π$ .

Đồng biến trên mỗi khoảng $(k π; π + k π)$ , $k \in Z$ .

Có đồ thị đối xứng qua gốc tọa độ.

B. Bài tập Hàm số lượng giác

Bài 1. Xét tính chẵn, lẻ của các hàm số sau:

a) f(x) = sinx cosx;

b) g(x) = sin²x + cos2x.

Hướng dẫn giải

a) Tập xác định của hàm số f(x) là D = ℝ.

Do đó, nếu x ∈ D thì –x ∈ D.

Ta có f(–x) = sin(–x) cos(–x) = –sinx . cosx = – f(x).

Vậy hàm số f(x) = sinx cosx là hàm số lẻ.

b) Tập xác định của hàm số g(x) là D = ℝ.

Do đó, nếu x ∈ D thì –x ∈ D.

Ta có g(–x) = sin²(–x) + cos2(–x) = [–sinx]² + cos(–2x) = sin²x + cos2x = f(x).

Vậy hàm số g(x) = sin²x + cos2x là hàm số chẵn.

Bài 2. Tìm tập giá trị của hàm số sau:

a) y = 1+ $\sqrt{\sin x}$ ;

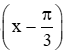
b) y = 3cos Lý thuyết Toán 11 Kết nối tri thức Bài 3: Hàm số lượng giác - 1.

Hướng dẫn giải

a) Điều kiện xác định của hàm số là sin x ≥ 0;

Vì –1 ≤ sin x ≤ 1 nên kết hợp với điều kiện xác định, ta có 0 ≤ sin x ≤ 1

Suy ra $0 \leq \sqrt{s inx} \leq 1$ ⇒ 1+0 $\leq$ 1 + $\sqrt{\sin x}$ $\leq$ 1 + 1 ⇒ 1 $\leq$ 1+ $\sqrt{\sin x}$ $\leq$ 2

⇒ 1 ≤ y ≤ 2

Vậy tập giá trị của hàm số y=1+ $\sqrt{\sin x}$ là [1; 2].

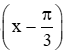
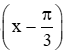
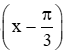
b) Ta có $- 1 \leq \cos$ Lý thuyết Toán 11 Kết nối tri thức Bài 3: Hàm số lượng giác $\leq$ 1, $\forall$ x $\in$ R ⇔ -3 $\leq$ 3cos $\leq$ 3, $\forall$ x $\in$ R

⇔ -4 $\leq$ 3cos Lý thuyết Toán 11 Kết nối tri thức Bài 3: Hàm số lượng giác - 1 $\leq$ 2, $\forall$ x $\in$ R

⇔ –4 ≤ y ≤ 2, ∀x ∈ ℝ.

Vậy tập giá trị của hàm số y = 3cos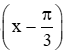 Lý thuyết Toán 11 Kết nối tri thức Bài 3: Hàm số lượng giác - 1 là [–4; 2].

Bài 3. Tìm tập xác định của các hàm số sau:

a) $y = \frac{1 + \sin x}{\cos x}$ ;

b) $y = \sqrt{\frac{1 + \cos x}{1 - \cos x}}$ .

Hướng dẫn giải

a) Biểu thức $\frac{1 + \sin x}{\cos x}$ có nghĩa khi cos x ≠ 0, tức là x ≠ $\frac{π}{2} + k π$ (k ∈ ℤ).

Vậy tập xác định của hàm số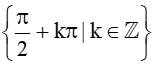 $y = \frac{1 + \sin x}{\cos x}$ là D = R\ Lý thuyết Toán 11 Kết nối tri thức Bài 3: Hàm số lượng giác .

b) Biểu thức $\sqrt{\frac{1 + \cos x}{1 - \cos x}}$ có nghĩa khi 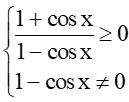Lý thuyết Toán 11 Kết nối tri thức Bài 3: Hàm số lượng giác (1)

Mặt khác, vì –1 ≤ cosx ≤ 1 ∀x ∈ ℝ nên 1 + cosx ≥ 0 và 1 – cosx ≥ 0

⇒ $\frac{1 + \cos x}{1 - \cos x} \geq 0$ khi 1 – cosx ≠ 0

Do đó (1) ⇔ 1 – cosx ≠ 0 ⇔ cosx ≠ 1 ⇔ x ≠ k2ℼ (k ∈ ℤ).

Vậy tập xác định của hàm số $y = \sqrt{\frac{1 + \cos x}{1 - \cos x}}$ là D = ℝ \ {k2ℼ | k ∈ ℤ}.

C. Trắc nghiệm Toán 11 Bài 3: Hàm số lượng giác

Câu 1. Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = 3sinx - 2

A. M = 1, m = -5. B. M = 3, m = 1

C. M = 2, m = -2 D. M = 0, m = -2.

Hiển thị đáp án

Đáp án đúng là: A

Ta có $- 1 \leq \sin x \leq 1 → - 3 \leq 3 \sin x \leq 3 → - 5 \leq 3 \sin x - 2 \leq 1$

$→ - 5 \leq y \leq 1 →$ 12 Bài tập Hàm số lượng giác (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 11

Câu 2. Trong các hàm số sau, hàm số nào là hàm số chẵn?

A. y = sin2x B. y = xcosx C. y = cosx.cotx D. y = $\frac{\tan x}{\sin x}$

Hiển thị đáp án

- Xét hàm số y = f(x) = sin2x.

TXĐ: D = $ℝ$ . Do đó $\forall x \in D \Rightarrow - x \in D.$

Ta có f(-x) = sin(-2x) = -sin2x = -f(x) $\to$ f(x) là hàm số lẻ.

-Xét hàm số y = f(x) = xcosx.

TXĐ: D = $ℝ$ . Do đó $\forall x \in D \Rightarrow - x \in D.$

Ta có f-x) = (-x).cos(-x) = -xcosx = -f(x) $\to$ f(x) là hàm số lẻ.

-Xét hàm số y = f(x) = cosx.cotx.

TXĐ: D = $ℝ$ \{k $π$ (k $\in$ $ℤ$ )}. Do đó $\forall x \in D \Rightarrow - x \in D.$

Ta có f(-x) = cos(-x).cot(-x) = -cosxcotx = -f(x) $\to$ f(x) là hàm số lẻ.

- D = $ℝ$ .Xét hàm số y = f(x) = $\frac{\tan x}{\sin x}$ .

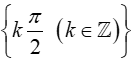
TXĐ: D = $ℝ$ \ 12 Bài tập Hàm số lượng giác (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 11 . Do đó $\forall x \in D \Rightarrow - x \in D.$

Ta có $f (- x) = \frac{\tan (- x)}{\sin (- x)} = \frac{- \tan x}{- \sin x} = \frac{\tan x}{\sin x} = f (x)$ $→ f (x)$ là hàm số chẵn.

Câu 3. Tìm tập giá trị của hàm số y = 3cos2x + 5

A. T = [-1;1]. B. T = [-1;11] C. T = [2;8] D. T = [5;8]

Hiển thị đáp án

Đáp án đúng là: C

Ta có -1 $\leq$ cos2x $\leq$ 1 $\to$ -3 $\leq$ 3cos2x $\leq$ 3 $\to$ 2 $\leq$ 3cos2x+5 $\leq$ 8

$\to$ 2 $\leq$ y $\leq$ 8 $\to$ T = [2;8].

Câu 4. Hàm số y = 5+4sin2xcos2x có tất cả bao nhiêu giá trị nguyên?

A. 3. B. 4. C. 5. D. 6.

Hiển thị đáp án

Đáp án đúng là: C

Ta có y = 5+4sin2xcos2x = 5+2sin4x. .

Mà -1 $\leq$ sin4x $\leq$ 1 $\to$ -2 $\leq$ 2sin4x $\leq$ 2 $\to$ 3 $\leq$ 5+2sin4x $\leq$ 7

→ y $\leq$ 7 $→ 3 \leq y \leq 7 \overset{y \in ℤ}{\to} y \in$ {3;4;5;6;7} nên y có 5 giá trị nguyên.

Câu 5. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = sinx + cosx. Tính P = M - m.

A. P = 4 B. P = 2 $\sqrt{2}$ C. P = $\sqrt{2}$ D. P = 2

Hiển thị đáp án

Đáp án đúng là: B

Ta có y = sinx + cosx = $\sqrt{2}$ sin $(x + \frac{π}{4})$ .

Mà -1 $\leq$ sin $(x + \frac{π}{4})$ $\leq$ 1 $\to$ - $\sqrt{2}$ $\leq$ $\sqrt{2}$ sin $(x + \frac{π}{4})$ $\leq$ $\sqrt{2}$

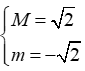
$\to$ 12 Bài tập Hàm số lượng giác (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 11 $\to$ P = M - m = 2 $\sqrt{2}$ .

Câu 6. Tìm chu kì T của hàm số y = cos2x + sin $\frac{π}{2}$

A. T = 4 $π$ B. T = $π$ C. T = 2 $π$ D. T = $\frac{π}{2}$

Hiển thị đáp án

Đáp án đúng là: A

Hàm số y = cos2x tuần hoàn với chu kì $T_{1} = \frac{2 π}{2} = π .$

Hàm số y = sin $\frac{x}{2}$ tuần hoàn với chu kì $T_{2} = \frac{2 π}{\frac{1}{2}} = 4 π .$

Suy ra hàm số y = cos2x + sin $\frac{x}{2}$ tuần hoàn với chu kì T = 4 $π$ .

Nhận xét. T là của T₁ và T₂

Câu 7. Tìm chu kì T của hàm số y = cos3x + cos5x.

A. T = $π$ B. T = 3 $π$ C. T = 2 $π$ D. T = 5 $π$

Hiển thị đáp án

Đáp án đúng là: C

Hàm số y = cos3x tuần hoàn với chu kì $T_{1} = \frac{2 π}{3} .$

Hàm số Y = cos5x tuần hoàn với chu kì $T_{2} = \frac{2 π}{5} .$

Suy ra hàm số y = cos3x + cos5x tuần hoàn với chu kì T = 2 $π$

Câu 8. Hàm số nào sau đây có chu kì khác $π$ ?

A. $y = \sin (\frac{π}{3} - 2 x) .$ B. $y = \cos 2 (x + \frac{π}{4}) .$

C. y = tan(-2x+1). D. y = cosxsinx

Hiển thị đáp án

Đáp án đúng là: C

Vì y = tan(-2x+1) có chu kì 12 Bài tập Hàm số lượng giác (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 11

Nhận xét. Hàm số y = cosxsinx = $\frac{1}{2}$ sin2x có chu kỳ là $π$ .

Câu 9. Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ?

A. $y = \frac{1}{\sin^{3} x} .$ B. $y = \sin (x + \frac{π}{4}) .$

C. $y = \sqrt{2} \cos (x - \frac{π}{4}) .$ D. $y = \sqrt{\sin 2 x} .$

Hiển thị đáp án

Đáp án đúng là: A

Viết lại đáp án B là $y = \sin (x + \frac{π}{4}) = \frac{1}{\sqrt{2}} (\sin x + \cos x) .$

Viết lại đáp án C là $y = \sqrt{2} \cos (x - \frac{π}{4}) = \sin x + \cos x .$

Kiểm tra được đáp án A là hàm số lẻ nên có đồ thị đối xứng qua gốc tọa độ.

Ta kiểm tra được đáp án B và C là các hàm số không chẵn, không lẻ.

Xét đáp án D:

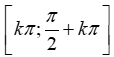
- Hàm số xác định $\Leftrightarrow$ sin2x $\geq$ 0 $\Leftrightarrow$ 2x $\in$ [k2 $π$ ; $π$ +k2 $π$ ] $\Leftrightarrow$ x $\in$ 12 Bài tập Hàm số lượng giác (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 11

-> D = 12 Bài tập Hàm số lượng giác (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 11 (k $\in$ Z).

- Chọn $x = \frac{π}{4} \in D$ nhưng $- x = - \frac{π}{4} \notin D.$ Vậy $y = \sqrt{\sin 2 x}$ không chẵn, không lẻ.

Câu 10. Tìm tập xác định D của hàm số $y = \frac{2021}{\sin x} .$

A. D = $ℝ$ B. D = $ℝ$ \{0}

C. D = $ℝ$ \{k $π$ , $\in$ $ℤ$ } D. D = $ℝ$ \

Hiển thị đáp án

Đáp án đúng là: C

Hàm số xác định khi và chỉ khi sinx $\neq$ 0 $\Leftrightarrow$ x $\neq$ k $π$ , k $\in$ $ℤ$ .

Vật tập xác định D = $ℝ$ \{k $π$ ,k $\in$ $ℤ$ }.

Câu 11. Trong các hàm số sau đây, hàm số nào không tuần hoàn?

A. y = cosx B. y = cos2x C. y = x²cosx. D. y = $\frac{1}{\sin 2 x}$

Hiển thị đáp án

Đáp án đúng là: C

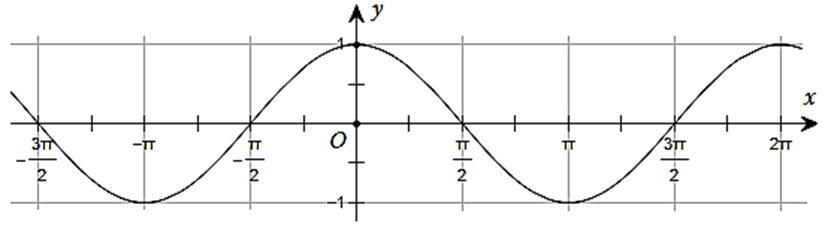
Câu 12. Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.

12 Bài tập Hàm số lượng giác (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 11

Hỏi hàm số đó là hàm số nào?

A. y = 1+sin2x B. y = cosx C. y = -sinx D. y = -cosx

Hiển thị đáp án

Đáp án đúng là: B

Ta thấy tại x = 0 thì y = 1. Do đó loại đáp án C và D.

Tại x = $\frac{π}{2}$ thì y = 0. Do đó chỉ có đáp án B thỏa mãn.

Xem thêm các bài tóm tắt lý thuyết Toán lớp 11 sách Kết nối tri thức hay, chi tiết khác:

Lý thuyết Bài 4: Phương trình lượng giác cơ bản

Lý thuyết Bài 5: Dãy số

Lý thuyết Bài 6: Cấp số cộng

Lý thuyết Bài 7: Cấp số nhân

Lý thuyết Bài 8: Mẫu số liệu ghép nhóm

1 3,623 16/09/2024

Trang trước

Trang sau

Xem thêm các chương trình khác:

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3