Nội dung bài viết

    Xem thêm

    Lý thuyết Cấp số cộng – Toán 11 Kết nối tri thức

    Với lý thuyết Toán lớp 11 Bài 6: Cấp số cộng chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sách Kết nối tri thức sẽ giúp học sinh nắm vững kiến thức trọng tâm để học tốt môn Toán 11.

    1 2,166 30/10/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Lý thuyết Toán 11 Bài 6: Cấp số cộng - Kết nối tri thức

    Bài giảng Toán 11 Bài 6: Cấp số cộng

    A. Lý thuyết Cấp số cộng

    1. Định nghĩa

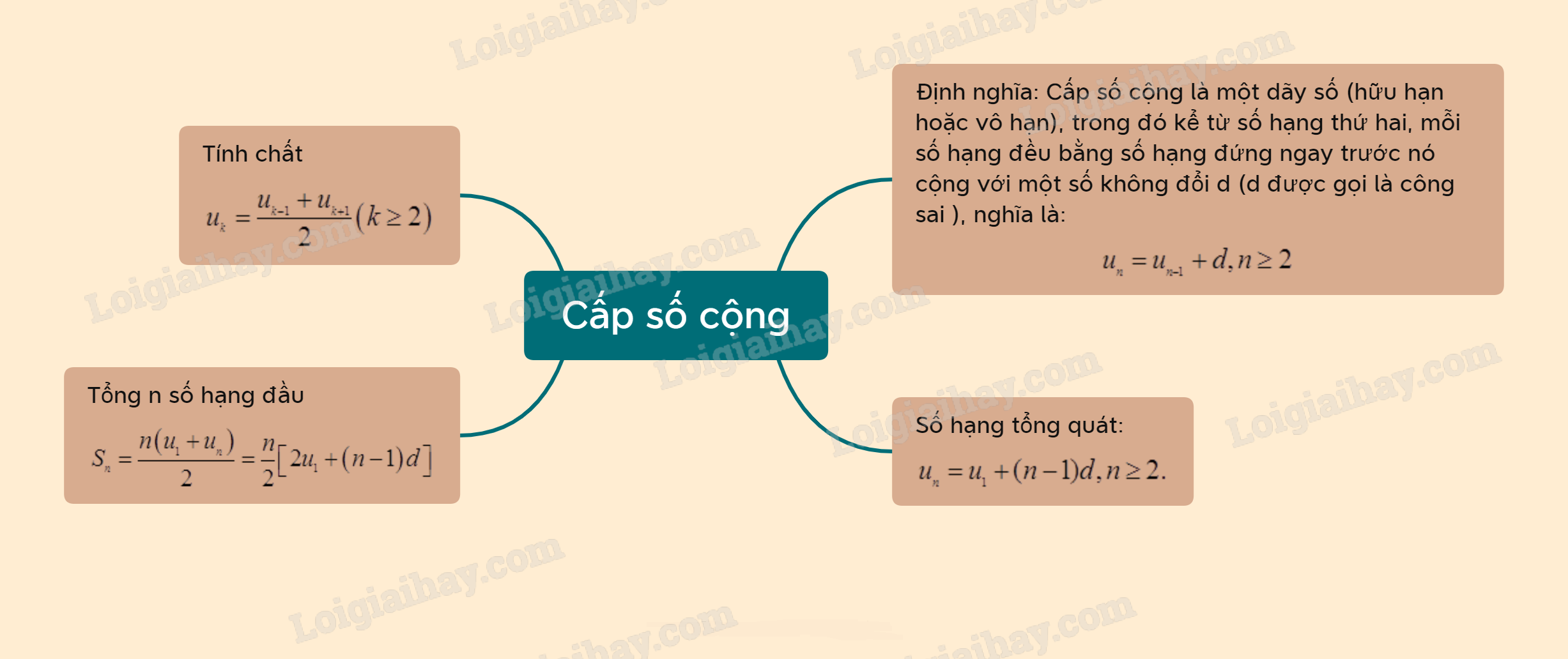
    Cấp số cộng là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đổi d. Số d được gọi là công sai của cấp số cộng.

    Cấp số cộng (un)với công sai d được cho bởi hệ thức truy hồi

    un=un−1+d,n≥2

    * Nhận xét: Nếu (un) là cấp số cộng thì kể từ số hạng thứ 2, mỗi số hạng (trừ số hạng cuối đối với cấp số cộng hữu hạn) đều là trung bình cộng của 2 sô hạng đứng kề nó trong dãy, tức là:

    uk=uk−1+uk+12(k≥2)

    2. Số hạng tổng quát

    Nếu cấp số cộng (un) có số hạng đầu là u1 và công sai d thì số hạng tổng quát uncủa nó được xác định theo công thức un=u1+(n−1)d,n≥2.

    3. Tổng n số hạng đầu của một cấp số cộng

    Cho cấp số cộng (un)với công sai d. Đặt Sn=u1+u2+u3+...+un. Khi đó

    Sn=n(u1+un)2=n2[2u1+(n−1)d]

    Lý thuyết Cấp số cộng – Toán 11 Kết nối tri thức (ảnh 1)

    B. Bài tập Cấp số cộng

    Bài 1: Một cấp số cộng có số hạng thứ 5 bằng 22 và số hạng thứ 12 bằng 43. Tìm số hạng thứ 50 của cấp số cộng này.

    Hướng dẫn giải

    Giả sử u1 là số hạng đầu và d là công sai của cấp số cộng đó. Ta có:

    u5 = u1 + 4d = 22

    u12 = u1 + 11d = 43

    Giải hệ phương trình gồm hai phương trình trên ta được u1 = 10 và d = 3.

    Vậy số hạng thứ 50 của cấp số cộng này là u50 = u1­ + 49d = 10 + 49 . 3 = 157.

    Bài 2: Xác định công sai, số hạng thứ 5, số hạng tổng quát và số hạng thứ 100 của mỗi cấp số cộng sau:

    a) 3, 8, 13, 18, ...;

    b) 1, –2, –5, –8, ...

    Hướng dẫn giải

    a) Ta thấy: 8 – 3 = 5; 13 – 8 = 5

    Suy ra cấp số cộng có u1 = 3, công sai d = 5

    Số hạng tổng quát của dãy số là: un = 3 + 5(n – 1) = 3 + 5n – 5 = 5n – 2.

    Số hạng thứ 5: u5 = 3 + 5 . (5 – 1) = 23

    Số hạng thứ 100: u100 = 3 + 5 . (100 – 1) = 498.

    b) Ta thấy: –2 – 1= –3; –5 – (–2) = –3

    Suy ra cấp số cộng có u1 = 1, công sai d = –3

    Số hạng tổng quát của dãy số là: un = 1 – 3(n − 1) = 1 – 3n + 3 = 4 – 3n.

    Số hạng thứ 5: u5 = 1 − 3. (5 – 1) = −11

    Số hạng thứ 100: u100 = 1 – 3. (100 – 1) = −296.

    Bài 3: Viết năm số hạng đầu của mỗi dãy số (un) sau và xét xem nó có phải là cấp số cộng không. Nếu dãy số đó là cấp số cộng, hãy tìm công sai d và viết số hạng tổng quát của nó dưới dạng un = u1 + (n – 1)d.

    a) un = 3 + 4n;

    b) un = 6n − 4;

    c) u1 = 3, un = un–1 + n.

    Hướng dẫn giải

    a) u1 = 7; u2 = 11; u3 = 15; u4 = 19; u5 = 23

    Ta có: un − un–1 = 3 + 4n − [3 + 4(n − 1)] = 4, với ∀n ≥ 2.

    Suy ra dãy số là cấp số cộng có u1 = 7 và công sai d = 4

    Số hạng tổng quát: un = 7 + 4(n − 1).

    b) u1 = 2; u2 = 8; u3 = 14; u4 = 20; u5 = 26

    Ta có: un − un–1 = 6n − 4 − [6(n − 1) − 4] = 6, với ∀ n ≥ 2.

    Suy ra dãy số là cấp số cộng có u1 = 2 và công sai d = 6.

    Số hạng tổng quát: un = 2 + 6(n − 1).

    c) u1 = 3; u2 = 5; u3 = 8; u4 = 12; u5 =17

    Ta có: u2 − u1 = 2 ≠ u3 – u2 = 3

    Suy ra đây không phải cấp số cộng.

    Bài 4: Vào năm 2020, dân số của một thành phố là khoảng 1,5 triệu người. Giả sử mỗi năm, dân số của thành phố này tăng thêm khoảng 15 nghìn người. Hãy ước tính dân số của thành phố vào năm 2030.

    Hướng dẫn giải

    Dân số mỗi năm của thành phố lập thành cấp số cộng có u1 = 1 500 (nghìn người), công sai d = 15.

    Dân số mỗi năm có dạng tổng quát là: un = 1 500 + 15(n − 1).

    Dân số của năm 2030 tức n = 11 thì u11 = 1 500 + 15 . (11 − 1) = 1 650 (nghìn người)

    Vậy ước tính dân số của thành phố năm 2030 là 1650 nghìn người hay 1,65 triệu người.

    Bài 5: Một cấp số cộng có số hạng đầu bằng 1 và công sai bằng 4. Hỏi phải lấy tổng của bao nhiêu số hạng đầu của cấp số cộng này để có tổng bằng 561?

    Hướng dẫn giải

    Gọi n là số các số hạng đầu cần lấy tổng, ta có:

    561 = Sn =n2[2.1+(n-1).4] = n2(-2+4n) = –n + 2n2

    Do đó 2n2 – n – 561 = 0.

    Giải phương trình bậc hai này ta được n = –16,5 (loại) hoặc n = 17.

    Vậy ta phải lấy 17 số hạng đầu của cấp số cộng đã cho để có tổng bằng 561.

    Xem thêm các bài tóm tắt lý thuyết Toán lớp 11 sách Kết nối tri thức hay, chi tiết khác:

    Lý thuyết Bài 7: Cấp số nhân

    Lý thuyết Bài 8: Mẫu số liệu ghép nhóm

    Lý thuyết Bài 9: Các số đặc trưng đo xu thế trung tâm

    Lý thuyết Bài 10: Đường thẳng và mặt phẳng trong không gian

    Lý thuyết Bài 11: Hai đường thẳng song song

    Tham khảo các loạt bài Toán 11 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 2,166 30/10/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: