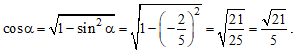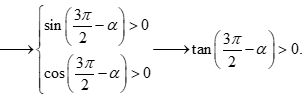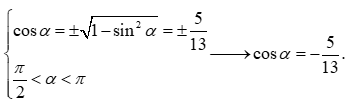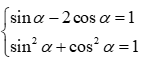Lý thuyết Giá trị lượng giác của góc lượng giác – Toán 11 Kết nối tri thức
Với lý thuyết Toán lớp 11 Bài 1: Giá trị lượng giác của góc lượng giác chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sách Kết nối tri thức sẽ giúp học sinh nắm vững kiến thức trọng tâm để học tốt môn Toán 11.
Lý thuyết Toán 11 Bài 1: Giá trị lượng giác của góc lượng giác - Kết nối tri thức
Bài giảng Toán 11 Bài 1: Giá trị lượng giác của góc lượng giác
A. Lý thuyết Giá trị lượng giác của góc lượng giác
1. Góc lượng giác
a, Khái niệm góc lượng giác và số đo của góc lượng giác
Trong mặt phẳng, cho 2 tia Ou, Ov. Xét tia Om cùng nằm tròn mặt phẳng này. Nếu tia Om quay quanh điểm O, theo một chiều nhất định từ Ou đến Ov, thì ta nói nó quét một góc lượng giác với tia đầu Ou và tia cuối Ov.
Kí hiệu: (Ou, Ov).
Số đo của góc lượng giác có tia đầu Ou và tia cuối Ov kí hiệu là sđ(Ou, Ov).
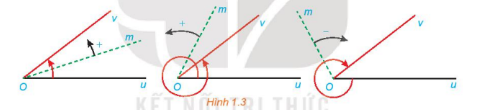
b, Hệ thức Chasles
Với 3 tia Ou, Ov, Ow bất kì ta có:
Sđ(Ou,Ov) + sđ(Ov, Ow) = sđ(Ou,Ow) +k360o.
2. Đơn vị đo góc và độ dài cung tròn
a, Đơn vị đo góc và cung tròn
Đơn vị độ:
Đơn vị rađian: rad, 1 rad =
b, Độ dài cung tròn
Một cung tròn của đường tròn bán kính R và có số đo rad thì có độ dài
3. Giá trị lượng giác của góc lượng giác
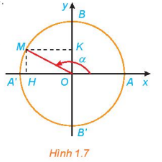
a, Đường tròn lượng giác
Đường tròn lượng giác là đường tròn có tâm tại gốc tọa độ, bán kính bằng 1, được định hướng và lấy điểm A(1;0) làm điểm gốc của đường tròn.
Điểm trên đường tròn lượng giác biểu diễn góc lượng giác có số đo (độ hoặc rad) là điểm M trên đường tròn lượng giác sao cho sđ (OA, OM) =.
b, Các giá trị lượng giác của góc lượng giác:
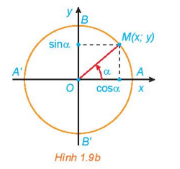
Trục tung là trục sin, trục hoành là trục côsin
Điểm M(x;y) nằm trên đường tròn như hình vẽ. Khi đó:
cos, sin.
tan
.
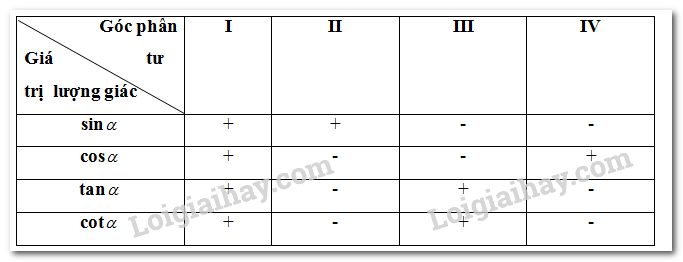
c, Bảng xác định dấu của các giá trị lượng giác
d, Giá trị lượng giác của các góc đặc biệt
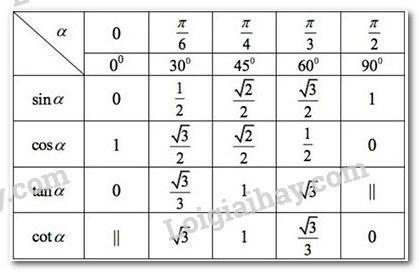
e, Cách bấm máy tính để tìm giá trị lượng giác của góc
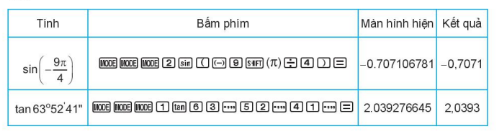
4. Quan hệ giữa các giá trị lượng giác
a, Các công thức lượng giác cơ bản
b, Giá trị lượng giác của các góc có liên quan đặc biệt (cos đối, sin bù, phụ chéo, khác pi tan)
-
Góc đối nhau ( và - )
-
Góc bù nhau ( và - )
-
Góc phụ nhau ( và - )
-
Góc hơn kém ( và + )
B. Bài tập Giá trị lượng giác của góc lượng giác
Bài 1. Tính các giá trị lượng giác của góc α, biết sinα = và .
Hướng dẫn giải
Vì nên cos α > 0. Mặt khác, từ sin2 α + cos2 α = 1 suy ra
Do đó, và .
Bài 2. Tính
a) 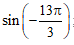
b) tan(–780°).
Hướng dẫn giải
a) 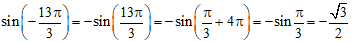
b) tan(– 780°) = tan(–60° – 2.360°) = tan(–60°) = – tan60° = .
Bài 3. Dùng máy tính cầm tay để:
a) Đổi 56°32’ sang rađian.
b) Tính 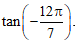
Hướng dẫn giải
a) Để đổi 56°32’ sang rađian ta bấm lần lượt như sau:
Màn hình hiển thị kết quả: 0,9866928038
Vậy 56°32’ bằng 0,9866928038 rađian.
b) Để tính 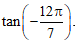
Màn hình hiển thị kết quả: 1,253960338
Vậy 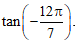
Bài 4. Trên một đường tròn có bán kính bằng 5 cm, tìm độ dài của cung có số đo .
Hướng dẫn giải
Ta có R = 5 cm; . Suy ra l = Rα = ≈ 10,5 (cm).
Vậy độ dài cung tròn là 10,5 cm.
C. Trắc nghiệm Toán 11 Bài 1: Giá trị lượng giác của góc lượng giác
Câu 1. Cho Khẳng định nào sau đây đúng?
A. tan<0. B. tan>0
C. tan0 D. tan0
Đáp án đúng là: B
Ta có
Câu 2. Tính giá trị biểu thức P = tan10o.tan20o.tan30o.....tan80o
A. P = 0 B. P = 1 C. P = 4 D. P = 8
Đáp án đúng là: B
Áp dụng công thức tanx.tan(90o-x) = tanx.cotx = 1.
Do đó P = 1.
Câu 3. Cho P = sin().cos() và Q = Mệnh đề nào dưới đây là đúng?
A. P+Q = 0 B. P+Q = -1 C. P+Q = 1 D. P+Q = 2
Đáp án đúng là: A
Ta có P = sin().cos() = -sin.(-cos) = sin.cos.
Và Q = = cos.(-sin) = -sin.cos.
Khi đó P+Q = sin.cos - sin.cos = 0
Câu 4. Biết A, B, C là các góc của tam giác ABC, mệnh đề nào sau đây đúng:
A. sin(A+C) = -sinB B. cos(A+C) = -cosB.
C. tan(A+C) = tanB D. cot(A+C) = cotB.
Đáp án đúng là: B
Vì A, B, C là ba góc của một tam giác suy ra A+C = -B.
Khi đó (A+C) = sin(-B) = sinB; cos(A+C) = cos(-B) = -cosB.
tan(A+C) = tan(-B) = -tanB; cot(A+C) = cot(-B) = -cotB.
Câu 5. Cho góc thỏa mãn sin = và . Tính cos.
A. cos = . B. cos = . C. cos = - D. cos = -.
Đáp án đúng là: D
Ta có
Câu 6. Cho góc thỏa mãn cot = . Tính
A. P = - B. P = . C. P = -13 D. P = 13.
Đáp án đúng là: D
Chia cả tử và mẫu của P cho sin ta được .
Câu 7. Cho góc thỏa mãn sin + cos = . Tính P = sin.cos.
A. P = . B. P = . C. P = . D. P =.
Đáp án đúng là: B
Từ giả thiết, ta có (sin+cos)2 = 1 +2sin.cos =
Câu 8. Cho góc thỏa mãn và sin-2cos = 1. Tính P = 2tan - cot.
A. P = . B. P = . C. P =. D. P = .
Đáp án đúng là: C
Với suy ra 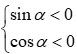
Ta có
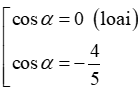
Từ hệ thức , suy ra (do sin<0) tan = và
Thay và vào P, ta được P = .
Câu 9. Khẳng định nào sau đây là đúng khi nói về “đường tròn lượng giác”?
A. Mỗi đường tròn là một đường tròn lượng giác.
B. Mỗi đường tròn có bán kính R = 1 là một đường tròn lượng giác.
C. Mỗi đường tròn có bán kính R = 1, tâm trùng với gốc tọa độ là một đường tròn lượng giác.
D. Mỗi đường tròn định hướng có bán kính R = 1, tâm trùng với gốc tọa độ là một đường tròn lượng giác.
Đáp án đúng là: D
Câu 10. Đổi số đo của góc 70o sang đơn vị radian.
A. B. C. D.
Đáp án đúng là:C
Áp dụng công thức với tính bằng radian, a tính bằng độ.
Ta có .
Câu 11. Tính độ dài l của cung trên đường tròn có bán kính bằng 20cm và số đo
A. l = 3,93cm. B. l = 2,94cm. C. l = 3,39cm D. l = 1,49cm
Đáp án đúng là:A
Áp dụng công thức
Câu 12. Với mọi số thực , ta có bằng
A. -sin B. cos C. sin D. -cos
Đáp án đúng là: B
Ta có
Xem thêm các bài tóm tắt lý thuyết Toán lớp 11 sách Kết nối tri thức hay, chi tiết khác:
Lý thuyết Bài 2: Công thức lượng giác
Lý thuyết Bài 3: Hàm số lượng giác
Xem thêm các chương trình khác:
- Soạn văn lớp 11 Kết nối tri thức - hay nhất
- Văn mẫu lớp 11 - Kết nối tri thức
- Tóm tắt tác phẩm Ngữ văn 11 – Kết nối tri thức
- Tác giả tác phẩm Ngữ văn 11 - Kết nối tri thức
- Giải SBT Ngữ văn 11 – Kết nối tri thức
- Bố cục tác phẩm Ngữ văn 11 – Kết nối tri thức
- Giải Chuyên đề học tập Ngữ văn 11 – Kết nối tri thức
- Nội dung chính tác phẩm Ngữ văn lớp 11 – Kết nối tri thức
- Soạn văn 11 Kết nối tri thức (ngắn nhất)
- Bài tập Tiếng Anh 11 Global success theo Unit có đáp án
- Giải sgk Tiếng Anh 11 – Global success
- Giải sbt Tiếng Anh 11 - Global Success
- Trọn bộ Từ vựng Tiếng Anh 11 Global success đầy đủ nhất
- Ngữ pháp Tiếng Anh 11 Global success
- Giải sgk Vật lí 11 – Kết nối tri thức
- Lý thuyết Vật lí 11 – Kết nối tri thức
- Giải sbt Vật lí 11 – Kết nối tri thức
- Giải Chuyên đề học tập Vật lí 11 – Kết nối tri thức
- Chuyên đề dạy thêm Vật lí 11 cả 3 sách (2024 có đáp án)
- Giải sgk Hóa học 11 – Kết nối tri thức
- Giải Chuyên đề học tập Hóa học 11 – Kết nối tri thức
- Lý thuyết Hóa 11 - Kết nối tri thức
- Giải sbt Hóa học 11 – Kết nối tri thức
- Chuyên đề dạy thêm Hóa 11 cả 3 sách (2024 có đáp án)
- Giải sgk Sinh học 11 – Kết nối tri thức
- Lý thuyết Sinh học 11 – Kết nối tri thức
- Giải Chuyên đề học tập Sinh học 11 – Kết nối tri thức
- Giải sbt Sinh học 11 – Kết nối tri thức
- Giải sgk Giáo dục Kinh tế và Pháp luật 11 – Kết nối tri thức
- Giải Chuyên đề học tập Kinh tế pháp luật 11 – Kết nối tri thức
- Lý thuyết Kinh tế pháp luật 11 – Kết nối tri thức
- Giải sbt Kinh tế pháp luật 11 – Kết nối tri thức
- Giải sgk Lịch sử 11 – Kết nối tri thức
- Giải Chuyên đề học tập Lịch sử 11 – Kết nối tri thức
- Lý thuyết Lịch sử 11 - Kết nối tri thức
- Giải sbt Lịch sử 11 – Kết nối tri thức
- Giải sgk Địa lí 11 – Kết nối tri thức
- Giải Chuyên đề học tập Địa lí 11 – Kết nối tri thức
- Lý thuyết Địa lí 11 - Kết nối tri thức
- Giải sbt Địa lí 11 – Kết nối tri thức
- Giải sgk Công nghệ 11 – Kết nối tri thức
- Lý thuyết Công nghệ 11 - Kết nối tri thức
- Giải sbt Công nghệ 11 – Kết nối tri thức
- Giải sgk Tin học 11 – Kết nối tri thức
- Giải Chuyên đề học tập Tin học 11 – Kết nối tri thức
- Lý thuyết Tin học 11 - Kết nối tri thức
- Giải sbt Tin học 11 – Kết nối tri thức
- Giải sgk Giáo dục quốc phòng an ninh 11 – Kết nối tri thức
- Lý thuyết Giáo dục quốc phòng 11 – Kết nối tri thức
- Giải sbt Giáo dục quốc phòng 11 – Kết nối tri thức
- Giải sgk Hoạt động trải nghiệm 11 – Kết nối tri thức